The transition from conservative to dissipative flows in class-B laser model with fold-Hopf bifurcation and coexisting attractors

Yue Li(李月) Zengqiang Chen(陈增强) Mingfeng Yuan(袁明峰) and Shijian Cang(仓诗建)

1College of Artificial Intelligence,Nankai University,Tianjin 300350,China

2Department of Earth and Space Science and Engineering,York University,4700 Keele St,Toronto M3J 1P3,Canada

3Department of Product Design,Tianjin University of Science and Technology,Tianjin 300222,China

Keywords: conservative flows, dissipative attractors, coexisting phenomena, fold-Hopf bifurcation, class-B laser chaotic system

1. Introduction

According to the conservative property of phase volume,the phase trajectories of the system can be divided into conservative flows (phase volume is conservative) and dissipative flows (phase volume is contractive). Since Lorenz proposed the Lorenz system in 1963,[1]dissipative systems have been extensively studied.[2–7]In recent years,with the further exploration of chaos theory, conservative flows have gradually become a research hotspot in the nonlinear field. For example, based on the generalized Hamiltonian system theory, the Cang team proposed a class of multi-cluster conservative chaotic systems (3D and 4D) with complex topological structures,[8–10]and the Dong team proposed some high-dimensional Hamiltonian conservative chaotic systems with multistability and designed a pseudo-random number generator.[11]In addition,the Qi team proposed some Hamiltonian conservative chaotic systems based on 4D Euler equations,and analyzed the reason why these systems can produce conservative chaos from the perspective of energy.[12,13]From the above introduction, it can be seen that the phase volume of the flows generated by the existing system is mostly single(conservative or dissipative). Based on this,this paper studies a class-B laser system, which can realize the transition from conservative flows to dissipative flows.

A laser is a device that emits light through a process of optical amplification or oscillation based on the stimulated emission of electromagnetic radiation.[14]In the 1980s,some scholars successively studied the class-B laser system with injected signal, and discovered chaos, Hopf bifurcation, and other dynamical behaviors.[15–17]In recent years,there are some scholars studying this system. Such the paper which analyzed the dynamic characteristics of a class-B laser model,it also found chaos by variable delayed optoelectronic feedback;[18]Wanget al.studied the Hopf bifurcation and double Hopf bifurcation phenomena of the class-B laser system;[14]Similarly,Li also investigated the double Hopf bifurcation of a class-B laser system.[19]However, the current researches on the class-B laser system are still subject to further exploration of chaos and Hopf bifurcation phenomena,and its internal dynamic characteristics had not been discovered yet. Therefore, this paper conducts deeper research on the class-B laser system. The contributions of this paper are as follows:

(i)Even if the system structure is not changed,the class-B laser system realizes the transition from conservative flows to dissipative attractors(period,quasi-period and chaos);

(ii) When the injected signal is not zero, there are two coexisting phenomena (period and period, period and quasiperiod)in the class-B laser system;

(iii) The class-B laser system has fold-Hopf bifurcation which is proved by the theoretical analysis and numerical simulation.

The rest of this paper is divided into six sections as follows. Section 2 introduces a class-B laser system and transforms this system into the generalized Hamiltonian system form. Section 3 analyzes the equilibria characteristics of the class-B laser system. In Section 4,the transition of the class-B laser system from conservative flows to dissipative attractors is analyzed. Section 5 introduces the coexisting phenomena in the system. The theoretical derivation and numerical simulation of the fold-Hopf bifurcation in the class-B laser system are introduced in Section 6. Finally,some conclusions are drawn in Section 7.

2. System description

By correcting the Maxwell–Bloch equations of a singlemode,homogeneously broadened ring laser with external signal, and separating the field variable into the amplitude and phase with respect to the external field,one gets a class-B laser system with injected signal:[17,20,21]

whereXis the state vector;A(X) is the skew-symmetric state matrix satisfyingA(X)=-A(X)T;Λ(X) is an indefinite matrix satisfyingΛ(X)=-Λ(X)T; ∇H(X) is the gradient vector of HamiltonianH(X); andUis a matrix composed of column vectors that represents the exchange energy between the system and the outside world. In terms of energy,A(X)∇H(X),Λ(X)∇H(X)andUrepresent the conservative term,the dissipative term,and the external interference of the system(3). Therefore,according to Eq.(3),the system(2)can be expressed as

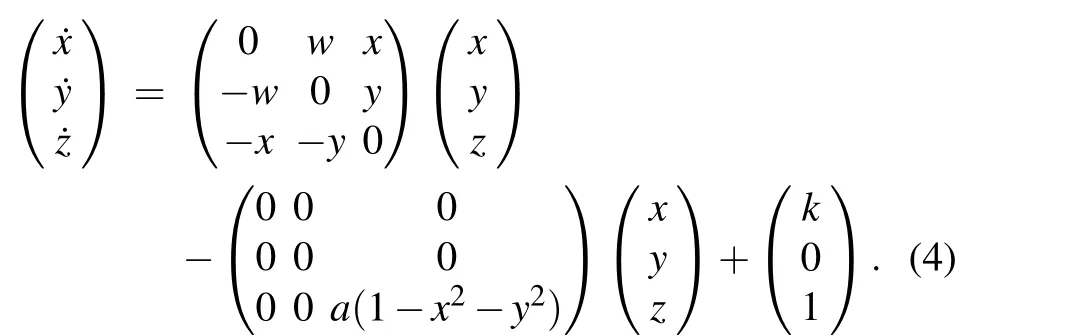
Obviously, the parameteradetermines the dissipative strength in system (2), this paper will discuss the dynamical characteristics of system(2)ata/=0.

3. Equilibrium analysis

Let ˙x= 0,˙y= 0,˙z= 0, the equilibrium points for system(2)are as follows:

(I)Whenk ∈(-w,w),system(2)has the only equilibrium

At this time,the system(2)has three equilibrium pointsS1,2,3.

It is difficult to produce the analytical solutions of the eigenvalues by substitutingS2,3into their corresponding Jacobian matrixes. For simplicity,leta=1 andw=1,then one can obtain the numerical results of the eigenvalues atS1,2,3whenkvaries, as shown in Fig. 1. As can be seen from the figure, when the parameterkpasses through the critical valuesw=±1, the equilibrium pointsS2,3will disappear or appear,which indicates thatSLandSRare the potential bifurcation points. Since the equilibria are symmetrical aboutk=0,this paper can only consider the dynamics of the system(2)atk≥0.

Fig. 1. Plot of the distribution of the equilibria of the system (2) with respect to k varying in the interval[-2,2],and their corresponding stability when a=1 and w=1. The blue and red curves are the marks of the stable and unstable equilibria,respectively. SL and SR denote the bifurcation points.

4. Transition from conservation to dissipation

Keepinga=1 andw=1, whenk=0, the phase trajectories of system (2) starting from different initial conditionsJ0=(0.2,0.1,0.1),J1=(0.3,0.1,0.1),...,J6=(0.8,0.1,0.1)form the nested quasi-periodic motions, their corresponding Poincar´e section is shown in Fig.2(a). The closed curves with different colors in Fig. 2(a) further indicate that there exist the coexistence of multiple quasi-periods in system (2) whenk=0. In addition, the Lyapunov exponents (LE1,LE2,LE3)=(0,0,0) indicate that these quasi-periodic motion are conservative flows. In the nonlinear system,since the dissipative term is difficult to keep balance with the conservative term and the external interference,it is difficult to find the conservative flows in the system containing the dissipative term. By calculation, the reason why the system (2) can produce conservative flows is that whenk=0,the dissipative term in system(2)is always in balance with the external interference, hence the nested closed curves in Fig.2(a)appear. And whenk/=0,the stable state in system (2) is destroyed due to the interference of the parameterk, that is, the closed curves in Fig. 2(a) will no longer exist. Figure 2(b)shows the Poincar´e section generated by system(2)atk=0.01,as we can see from the figure,the seemingly closed rings are actually some irregular discrete points,these show that whenk=0.01,the quasi-periodic motions are disturbed and turn into chaotic motion.

With the continuous increase of the value ofk,the dissipative characteristics of system (2) are also becoming more and more obvious. Figure 3 shows the Lyapunov exponents of system (2) whilek ∈[0.2,0.7]. It can be seen from the figure that whenktakes different values, the system (2) has dynamical behaviors with different characteristics. For example, whenk= 0.4, the Lyapunov exponents(LE1,LE2,LE3) = (0,-0.13,-0.13) indicate that there is a periodic orbit in system (2); whenk= 0.55, the Lyapunov exponents (LE1,LE2,LE3) = (0,0,-0.14) indicate that system (2) has quasi-periodic motion; and the Lyapunov exponents(LE1,LE2,LE3)=(0.14,0,-0.24)whenk=0.67 indicate that the system(2)has chaotic motion. These phenomena are shown in Fig.4.

Fig.2. When the parameters a=1 and w=1,Poincar´e sections of the system(2)on the x–z plane(y=0)with different initial conditions J0,1,...,6: (a)k=0;(b)k=0.01.

Fig.3. When the parameters a=1,w=1,Lyapunov exponents of the system(2)from the initial conditions I0=(0.1,0.1,0.1)with k ∈[0.2,0.7].

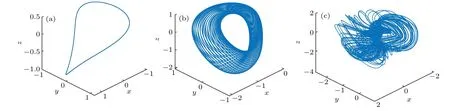
Fig.4. When the parameters a=1,w=1,3D phase portraits the system(2)from the initial conditions I0=(0.1,0.1,0.1)with different k: (a)k=0.4;(b)k=0.55;(c)k=0.67.

5. Coexisting phenomena

According to the Section 4,whena=1,w=1 andk/=0,no matter what motion(period,quasi-period,or chaos)is produced by system (2), its phase volume is always contractive.That is to say,the phase trajectories in Fig.4 are independent attractors. However, through numerical simulation, it is finds that system(2)has not only one attractor,but also two attractors in special cases,that is,coexisting attractors.

Figure 5(a) shows the two coexisting periodic attractorsP1andP2which exist in the system (2) whenk=0.3,which are generated by the initial valuesP1=(0.8,0.5,0.5)andP2=(0.5,0.5,0.5), respectively. In addition, whenk=0.89, the system (2) also has the coexisting phenomenon.By choosing the initial conditionsN1=(0.5,-0.6,0.5) andN2=(0.5,0.5,0.5),and they generate the quasi-periodic motionN1and the periodic motionN2as shown in Fig.5(b),respectively.

Fig. 5. The 3D phase portraits of system (2) with the parameters a =1,w=1: (a) parameter k =0.3 and the initial values P1 =(0.8,0.5,0.5)and P2 =(0.5,0.5,0.5); (b)parameter k=0.89 and the initial values N1 =(0.5,-0.6,0.5)and N2=(0.5,0.5,0.5).

Under given parameter conditions, according to whether the basin of attraction of attractor contains the equilibrium point in phase space,attractor can be divided into self-excited attractor or hidden attractor.[23]The basin of attraction of self-excited attractor contains the equilibrium point,while the basin of attraction of hidden attractor does not contains the equilibrium point. Whena=1,w=1 andk ∈(-w,w), according to Eq.(5),we have a single equilibrium point Further, whenk= 0.3 ork= 0.89, one can get ˜S1=(-0.15,-0.15,1)or ˆS1=(-0.445,-0.445,1).

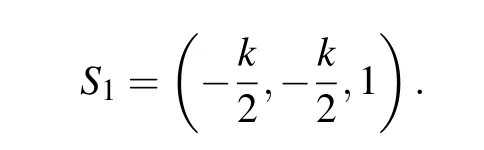
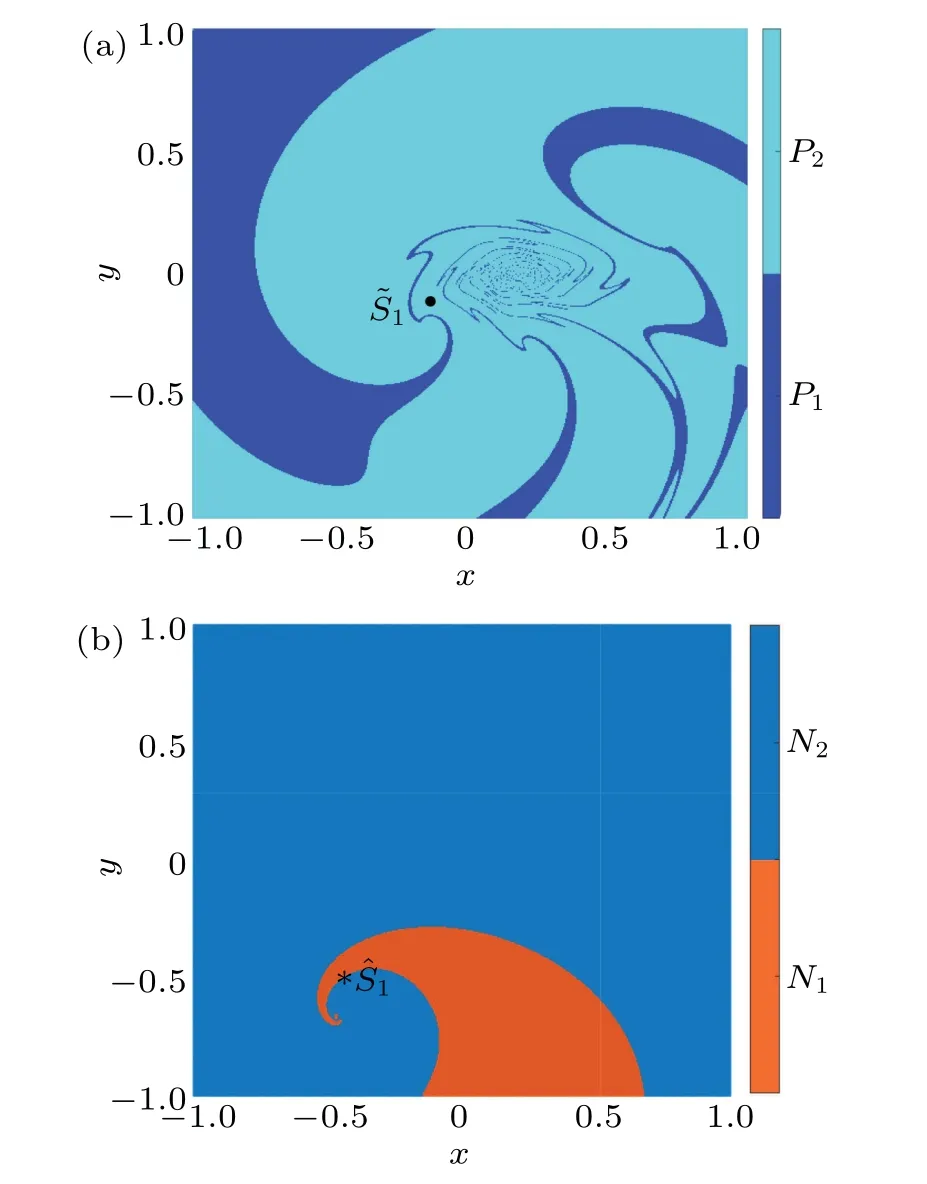
Fig.6. Two colored basins of attraction of system(2)at z=0.5 on the x–y plane;(a)k=0.3;(b)k=0.89.

In order to determine the type of attractors shown in Fig.5,figures 6(a)and 6(b)show the basin of attraction of system(2)whenk=0.3 andk=0.89,respectively. In Fig.6(a),the dark blue area represents the basin of attraction of periodic motionP1in Fig.5(a),the light blue area represents the basin of attraction of periodic motionP2, and the equilibrium point ˜S1is represented by “·”. It can be seen from the figure that equilibrium point ˜S1is located in the light blue area,which indicates that the periodic motionP2in Fig.5(a)is a self-excited attractor,and the periodic motionP1is a hidden attractor. Further,in Fig.6(b),the red area represents the basin of attraction of quasi-periodic motionN1in Fig. 5(b), the blue area represents the basin of attraction of periodic motionN2, and the equilibrium point ˆS1is represented by“*”. Obviously,the different colors do not intersect each other,but this is enough to determine the type of the two attractorsN1andN2in Fig.6(b).

To further determine the type of attractorsN1andN2,one keeps the parametersaandwunchanged,and chooses an initial valuesX0=(-0.445,-0.445,0.9999)that are very close to the equilibrium points ˆS1. Whenk=0.89, the study finds that the motionX0(Fig. 7) starting from the initial valueX0similar to that of the periodic motionN2in Fig. 5(b). This shows that the basin of attraction of the periodic motionN2intersects with open neighborhood of the equilibrium point ˆS1,which in turn indicates that the periodic orbitN2is a selfexcited attractor,and the quasi-periodic motionN1is a hidden attractor.

Fig. 7. The 3D phase portraits of system (2) with the parameters a=1,w=1,k=0.89 and the initial conditions X0=(-0.445,-0.445,0.9999).

6. Fold-Hopf bifurcation

6.1. Derivation of the normal form

The fold-Hopf bifurcation is a bifurcation of an equilibrium point in a two-parameter family of autonomous ODEs at which the critical equilibrium has a zero eigenvalue and a pair of purely imaginary eigenvalues.[24]Consider an autonomous system of ordinary differential equations(ODEs):

According to formula(14),the fold-Hopf bifurcation can be divided into three categories:

I)subcritical Hopf bifurcation and no tori(s=1,θ(0)＞0 ors=-1,θ(0)＜0);

II) subcritical and supercritical Hopf bifurcations and torus“heteroclinic destruction”(s=1,θ(0)＜0);

III) subcritical and supercritical Hopf bifurcations and torus“blow-up”(s=-1,θ(0)＞0).

6.2. Theoretical analysis

Proposition 1 Whena= 1 andw= 1, andkpasses through the critical values 1,system(2)undergoes a fold-Hopf bifurcation and presents a blow-up invariant tori near the fold-Hopf bifurcation point.

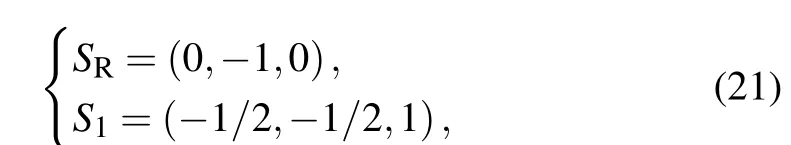
Proof Whena=1,w=1 andk=1,system(2)has two equilibrium points:Then, one gets the coefficients of the Gavrilov normal form:B(0)=-1/3,C(0)=16/9 andE(0)=11/48. Furthermore,we have

In conclusion, whena=1,w=1, andk=1, there is a fold-Hopf bifurcation point in system(2),ands=-1,θ(0)＞0 indicate that a blow-up invariant tori appears near the fold-Hopf bifurcation point.

6.3. Numerical simulation

In this section,one further verifies the correctness of the Proposition 1 through numerical simulation. As shown in Fig.8(a),at the fold-Hopf bifurcation point,the phase trajectoryφ(X0,t)converges toSR,whilek=0.991,an invariant torus is suddenly blow-up andφ(X0,t) runs on it eventually.Two black closed curves on thex–zplane in Fig. 8(b) further show that system (2) is quasi-periodic. The red points approaching the black closed curves demonstrate that the motion of system (2) gradually reaches the invariant torus over time whenk=0.99.

Fig.8. Invariant torus of system(2)with the parameters a=1,ω =1,k=0.99 1 and the initial conditions X0 =(0.5,0.5,0.5): (a) phase portrait on the x–y plane;and(b)Poincar´e section on the x–z plane with y=-1.

7. Conclusion

In this paper, A class-B laser system with conservative and dissipative characteristics was studied. The study found that the numbers and stability of equilibrium points are affected by the system parameters. Whenk=0, there are conservative flows in the class-B laser system. Whenk/=0, the conservative characteristics disappear and the dissipative characteristics become more and more obvious. Meanwhile, it is found that there are period, quasi-period, chaos, and coexisting attractors in system, these phenomena have been demonstrated by several numerical techniques including phase portraits,Poincar´e sections,Lyapunov exponents,and other tools.In addition,through theoretical derivation,we find that the system has a fold-Hopf bifurcation and tori will“blow-up”at the bifurcation point, and the subsequent numerical simulations confirm the correctness of the theoretical derivation.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 61973175) and the Natural Science Foundation of Tianjin(Grant Nos.20JCYBJC01060 and 20JCQNJC01450).