锂离子电池容量衰减诊断方法
2022-06-29钱东培姜炯挺杨跃平王炯耿刘双宇许君杰王丹妮
钱东培,姜炯挺,杨跃平,王炯耿,董 栋,刘双宇,许君杰,王丹妮
(1.浙江华云信息科技有限公司,浙江 杭州 310008; 2.国网浙江省电力有限公司宁波供电公司,浙江 宁波 315016)
1 前 言
锂离子电池因其能量密度高、使用寿命长等优势在新能源汽车、消费电子及大规模储能等领域实现了广泛应用。作为一类电化学储能器件,锂离子电池通过一系列的化学反应,实现电能与化学能的相互转换。在电池使用过程中,由于副反应的发生或机械碰撞、异常温升等外部因素,会使电池出现不同程度的老化,造成可用容量衰减[1]。
为了准确评估电池老化状态,保证电池系统安全、可靠运行,除了获取电池可用容量的准确数据外,还需针对电池服役过程中造成容量损失的内在机制做出有效诊断。然而,锂离子电池容量衰减过程是多种损失机制共同参与、相互作用的结果,随着老化程度加深,导致容量衰减的主导机制也会发生变化,进而引起容量衰减趋势的变化[2-5]。精确、可靠地诊断电池容量衰减机制一直是对科研技术人员的重要挑战。
锂离子电池开路电压(OCV)是电池正极和负极电势之间的差值,其包含了任意时间节点电池电极的热力学信息,通过对OCV曲线的分析可以得到电池内部组分的衰减信息,因此得到研究人员的广泛关注。如通过电增量曲线分析(ICA)和差分电压分析(DVA)可以在仅获得电池电压、电流等外特性测量数据的基础上,对电池衰减机制和衰减程度进行定性分析,但这两种方法无法获得电池内部组分衰减的信息[6-10]。
根据电池OCV与正负电极电势之间的数值关系[11],测试分析半电池和全电池OCV的变化,可以确定电池衰减过程中可用锂离子损失(LLI)和活性材料损失(LAM)对于容量衰减的贡献[12-14]。但是目前这些模型需要计算模拟结果相对所有OCV测试值的误差,计算量大且无法避免数据噪声的影响。
本研究以三元锂离子电池为主要研究对象,开展电池容量衰减分析方法研究。基于半电池电极电势曲线和全电池OCV分析,通过分段非线性回归建模方法获得高精度的IC曲线和OCV曲线模型,进而重构计算全电池OCV曲线。采用该模型定量分析电池可用锂离子损失、正负极活性材料损失,快速、低成本地分析电池老化程度和衰减机制;同时,分段非线性回归处理保留了OCV数据中电极材料相变信息,以获得的高精度OCV曲线数值模型作为性能分析的基础,在提升曲线重构计算精度的同时,通过调整计算步长减少计算时间,使模型具有更强的适用性和准确性。
2 实 验
使用额定容量2500 mAh的商用18650 三元锂离子电池(NCM523)为研究对象,进行循环老化测试。电池测试在恒定室温下(25 ℃)进行,使用深圳新威尔BTS-5V3A测试仪,最大电压采样频率10 Hz。
为获得电池实际最大容量,每个电池在开展实验前先以1 C倍率正常循环3次确认处于正常状态,然后以1/25 C倍率进行充放电,充电截止电压4.2 V,放电截止电压2.75 V。由于此时电流足够小,电池内部极化影响可以忽略,故可以认为此时电池处于准平衡态,此时的容量-电压曲线(Q-V)即为电池的OCV曲线。采用直流脉冲电流测试电池内阻,将电池以1 C倍率放电至50% SOC后静置15 min,记录电压变化并计算电池欧姆内阻和极化内阻。
循环老化测试条件采用1 C倍率的CCCV-CC充放电规程,即恒流充电至截止电压4.2 V后,继续恒压充电至截止电流1/20 C。电池A和电池B分别以1C和0.5 C放电至截止电压2.75 V,每循环50次,测试一次Q-V曲线。
3 数学模型
3.1 锂离子电池容量衰减机制
根据电池内部材料组分损失情况,锂离子电池容量衰减机制可以归结为可用锂离子损失(LLI)和电极活性材料损失(LAM)两种机制,其中电极活性材料损失又包括正极含锂(LAMliPE)/不含锂活性材料损失(LAMdePE)、负极含锂(LAMliNE)/不含锂活性材料损失(LAMdeNE)[13]。不同衰减机制会引起电池电极电势曲线变化[15],如图1所示,其中PE、NE分别表示未衰减电池内正极、负极容量,APE、ANE分别表示老化过程中电池内可用的正极活性材料、负极活性材料的容量。

图1 不同容量损失机制导致的电极电势曲线变化[16]Fig. 1 Change of the electrode potentials result from different degradation modes[16]
全电池OCV可以表示为正负极OCV之间的差值,如图2所示[11]。其中OCV(Q)表示全电池开路电压,UPE、UNE分别表示正负极对锂电势,η为过电势修正值。正负极可用活性材料容量QPE、QNE与可用锂离子总量QLI可由式(1)计算得到。式中QPE,initial、QNE,initial分别为电池循环开始时的正极容量和负极容量,ΔQ为充电容量或放电容量,SOCPE、SOCNE分别为正负极荷电状态,SOCPE,0、SOCNE,0分别为充放电开始时的电极SOC。

图2 锂离子电池OCV重构模型Fig. 2 OCV reconstruction model of lithium ion batteries
(1)
3.2 OCV曲线重构模型
由图2所示的OCV模型可知,全电池电压OCV、正极电势UPE和负极电势UNE均随着充放电容量ΔQ的变化而变化,因而可以得到一个以ΔQ为自变量的多元高阶函数。在全电池开路电压OCV、正极电势UPE和负极电势UNE三个数值模型均已知的情况下,求解最优未知参数组合,定量得到正负极活性材料损失、可用锂离子损失,进而评估电池健康状态以及容量衰减关键影响因素。
实验测得的电池电压曲线是非均匀的离散数据,且包含有大量噪声,无法直接代入上述模型中进行计算。可采用分段多项式拟合的方式将电极电势和电池OCV曲线拟合为电化学窗口内多组连续的分段函数,再通过电池OCV重构模型计算出全电池电压,电池模型求解流程如图3所示。具体步骤如下:

图3 电池模型参数求解流程Fig. 3 Flowchart of model parameters recognition
①根据测试数据描绘IC曲线;②根据IC曲线特征峰对其进行分段多项式拟合,作为一个连续分段函数;③对IC曲线积分后获得OCV曲线模型;④重构全电池OCV曲线,模拟计算最优模型参数组:(a) 设置初始参数[SOCPE,0SOCNE,0QPEQNEη]0;(b) 计算此时对应的RMSE0;(c) 设置步长f(RMSE0),并使得[SOCPE,0SOCNE,0QPEQNEη]1=[SOCPE,0SOCNE,0QPEQNEη]0+f(RMSE0);(d) 计算[SOCPE,0SOCNE,0QPEQNEη]1对应的RMSE1,设置步长f(RMSE1);(e) 比较所有RMSEi,输出min (RMSE)对应的参数[SOCPE,0SOCNE,0QPEQNEη],即为所求的最优解。
由式 (1) 和图2可知,对于确定的Q0和ΔQ步长,每一组[SOCPE,0SOCNE,0QPEQNEη]都对应了一条全电池模拟电压曲线,采用随机森林搜索算法可以获得一组最优参数,使得RMSE值最小,即可以认为是电压重构模型的最优解。RMSE可由下式计算得到:
(2)
4 结果与讨论
4.1 模型的验证
电池IC曲线将OCV曲线中的电压平台显示为可识别的峰,反映了脱嵌锂过程中电极材料的相变[10]。图4 (a) 为NCM三元锂离子电池IC曲线和OCV曲线的拟合结果,根据IC曲线峰对其分段不仅可以提高拟合精度,同时可以保留电池充放电过程中电极材料的相变信息,保证诊断结果的可靠性。图4 (b) 中OCV相对误差小于0.20%,显示精度较高。

图4 NCM/GC电池的 (a) IC曲线;(b) OCV曲线拟合结果Fig. 4 Fitting results of NCM/GC battery (a) IC curve, (b) OCV curves
基于电压曲线拟合结果,通过图2所示的模型重构OCV曲线,计算所述的电池模型参数。其中正负极SOC-OCV曲线是通过将新电池拆解重组半电池后,再测试其OCV曲线获得。分别模拟不同参数组合对应的电极电势曲线及电池OCV曲线,计算其与拟合值之间的均方差,并得到最小误差结果,如图5所示。这里取ΔQ=5 mAh,求最优解得到RMSE小于10 mV,表明模型具有较高的准确性。

图5 OCV曲线重构计算结果Fig. 5 Calculation results of OCV reconstruction model
4.2 电池循环过程中衰减行为分析
4.2.1循环过程中的容量衰减 以上文所述的电池容量衰减机制诊断方法,分析电池A和B循环过程中的衰减行为,电池A全电池平衡电压变化曲线如图6(a) 所示。随着循环次数增加,电池容量逐渐衰减,至200次后,电池容量已衰减至初始容量80%以下,且后期容量衰减速度逐渐增大。循环过程中全电池容量衰减及内部组分衰减量计算结果如图6(b) 所示。随着循环次数增加,全电池容量在老化初期线性下降,但其衰减速度在循环100次之后显著加快。QPE、QNE、QLI明显衰减,其中QLI与QPE在前100次稳定衰减,之后与全电池容量类似,呈现指数形式快速衰减;QNE在全周期内近似线性稳定衰减,表明三元锂离子电池中PE相对于NE活性材料更易在循环中损失。电池循环后期,容量的加速衰减与电池正极活性材料损失以及电池可用锂离子损失密切关联。
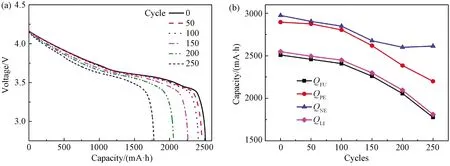
图6 电池A循环过程中的 (a) 容量变化;(b) 电池材料容量衰减Fig. 6 Evaluation of (a) capacity and (b) active materials of battery A during cycling
电池B循环过程中的OCV曲线以及容量变化如图7所示,虽然电池B放电电流相对电池A小,但其容量衰减趋势与A接近。循环100次后,电池容量出现跳水现象,且QPE和QLI衰减趋势与全电池容量相似,循环100次后快速下降,QNE在循环过程中整体呈现线性下降。模拟计算结果表明,对于三元锂离子电池,三元电极材料相较于石墨负极稳定性更差,循环过程中正极材料的衰减LAMPE是影响电池容量损失的关键因素。充电倍率相同时,将放电电流由1 C减小至0.5 C并不能明显改善电池循环寿命。

图7 电池B循环过程中的(a) 容量变化,(b) 电池材料容量衰减Fig. 7 Evaluation of (a) capacity and (b) active materials of battery B during cycling
4.2.2电池内阻变化 采用直流脉冲电流测试电池内阻[17-18],R1为电池静置初始阶段电压瞬间变化对应的电阻,主要由欧姆内阻组成,包括集流体、隔膜以及SEI产生的阻抗。R2对应静置阶段的渐变电压,由电荷不均匀分布导致的电池极化内阻组成。电池A、B循环过程内阻变化如图8所示,循环过程内阻逐渐增大且明显分为两个阶段,循环后期内阻增长速度突然加快。但与容量衰减行为相比,其稳定增长阶段与加速增长阶段的拐点均在循环100~150次之间,略微晚于发生容量“跳水”的循环次数。虽然电池内阻增长也作为表征电池SOH的关键参数[19],但是单一内阻测试可能无法准确表征电池内部组分容量衰减模式,因为某些条件下电池LAM或者LLI并不能体现为内阻增加,如SEI形成与分解是同时发生的,循环前期LLI并不会表现为R1快速增长。基于OCV分析的电池容量衰减诊断方法具有更好的精度和可靠性。

图8 电池循环过程中电池内阻变化 (a)电池 A;(b) 电池 BFig. 8 Evaluation of internal resistance during cycling, (a) battery A and (b) battery B
5 结 论
针对锂离子电池服役过程全生命周期的老化行为,研发了一种电池容量衰减机制诊断方法。以商用三元锂离子电池为研究对象,通过对电池IC曲线进行分段非线性回归拟合,获得高精度的OCV曲线数值模型。并在此基础上,通过OCV重构模型结合改进的随机搜索算法对电池容量衰减行为进行了定量分析。通过该方法可以计算电池循环过程中的LAM和LLI,相比单一进行电池内阻测试具有更高的可靠性,为确定电池容量衰减内在机制以及预测潜在的系统风险提供了依据。本研究提出的电池容量衰减诊断方法,可应用于动力电池或者储能电池系统从选型至梯次利用的全生命周期维护中,为优化电池系统运行维护策略提供数据支持,具有重要的实践意义。
