抽水蓄能电站地下水位预测的优化神经网络模型

郭浩然 ，李 映 ，黄鹤程

（1．中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳 550081；2．南方电网调峰调频发电有限公司，广东 广州 510630）

0 引言

输水系统沿线山体地下水位变化可能造成地面沉降、滑坡、深埋隧洞开挖施工过程中涌水等安全事故，同时，大坝蓄水后水-岩相互作用也可能会诱发地震。地下水位监测是抽水蓄能电站安全监测中重要的一个项目，通过对输水系统沿线山体地下水位的监测，可以对引水系统内各部位进行压力及地质环境分析。同样地下水位预测可以为工程建设、地震预报等提供参考[1]，进而保证抽水蓄能电站的安全稳定运行。

早期地下水位预测常用解析法与数值法：解析法假设地下水实际含水层为均质且形状规则，抽水蓄能电站上、下库落差较大，工区内地下水通常分布不均，使用该方法的地下水位模型并不适用于地下水的区域性研究中；数值法则需要获取水文地质条件及参数，人工工作量较大且操作复杂。随着计算机技术的发展，小波分析、灰色理论、马尔科夫链、人工神经网络等方法都是地下水位预测的常用方法[2]。各方法都有各自的优缺点，神经网络近年发展迅速，此方法在工业、水文分析、预测等领域应用广泛且效果理想，但其自身存在泛化能力弱、局部最优等问题[3]。

结合主成分分析（PCA）、遗传算法（GA）优化 BP 神经网络，通过主成分分析对数据进行预处理可减少样本维度，再通过遗传算法优化神经网络初始参数，可提高神经网络泛化能力并克服其局部最优问题，用于对水位孔地下水位的预测。本研究以广东某抽水蓄能电站用于监测输水系统沿线山体地下水位的 UP-1 水位孔测点为例，结合易获得的实际监测环境量，研究优化后神经网络模型对地下水位值的预测效果。

1 基本原理介绍

1.1 主成分分析

主成分分析法的核心思想是：通过正交变换把1 组可能存在相关性的变量变换成 1 组线性无关的量，得到的变量即为主成分。在实际应用中用 PCA法对数据进行预处理，尤其在样本维数较多时可以达到减少输入样本维度、提高训练效率的目的；同时，使用 PCA 方法可以减少部分数据冗余及噪声，提高网络模型训练效率及泛化能力[4]。

设有p个随机变量指标X1，X2，…，Xp，记为X=（X1，X2，…，Xp）T，取自X的容量为n的随机样本为xi（i= 1，2，…，n），其协方差矩阵为，特征值为λ1≥λ2≥ … ≥λp≥ 0，相应单位正交向量为e1，e2，…，ep，则第i个主成分yi为

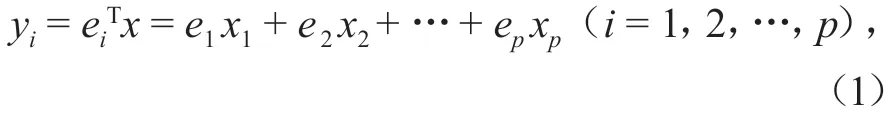
式中：ei=（e1，e2，…，ep）T。

X的任一观测值x=（x1，x2，…，xp）T，代入X的观测值便可以求得第i个样本主成分的观测值yk i（k= 1，2，…，n），第i个特征值与所有特征值之和的比值称为该特征值的主成分贡献率。

实际应用中可以选取贡献率最大的数个特征值作为主成分，使其累计贡献率达到一定比例，代替前原始数据用作分析计算，这样可以充分反映原变量包含的信息，新指标间互不相关。

1.2 遗传算法

遗传算法属于仿生智能算法，是一种基于生物进化论中的理论而提出的优化方法，该方法模仿了环境变化下，生物染色体变异、交叉并最终进化且体现在生理上。遗传算法在算法前，初始化种群并利用常用的二进制编码进行编码，在算法结束时将其解码得到优解。根据需求建立不同的适应度函数，对不同个体、种群进行优胜劣汰，通过多次的选择、交叉、编译使得种群的适应度朝着目标进化，在每次操作后对种群的适应度进行评估，淘汰适应度低的种群，并将优秀种群进行交叉、变异以得到新种群。当种群的平均适应度超过了设定值，适应度最大的个体达到目标或完成进化迭代设定值后，将最佳染色体选解码作为优化计算的最优解。遗传算法在自动控制、机器学习、目标优化等领域应用十分广泛。

1.3 BP 神经网络

BP 神经网络是一种多层的前进型并带有反向传播的网络，其结构一般包含 1 个输入层、输出层，以及 1 个或多个隐含层，输入层的神经元使用上下层全连接的方式经过隐藏层再通过输出层得到结果，根据不同的情景运用不同的激活传递函数，在对结果值与期望值进行比较后，通过反向传播不停调整网络参数，当结果值与期望值误差达到预期后即得到训练后的神经网络模型。BP 神经网络的核心思想为输入与输出层之间的正向与反向传播。

BP 神经网络的优点在于可以通过学习和训练处理复杂的非线性问题，在预测领域也表现出强大的能力。网络学习过程使用的是梯度下降法，存在收敛速度慢、陷入局部最优等问题，因此网络内各初始参数的选取对网络的性能有着不小的影响[5]。

2 地下水位影响因素分析

2.1 测点及测站布置

广东某抽水蓄能电站处于北回归线以南，属亚热带季风气候，雨量充沛，冬季温暖，夏季多雨，4—6 月多为锋面雨，7—9 月多为台风雨，4—9 月雨量占全年雨量的 80% 以上。上、下水库设计正常蓄水位高差为 670.0 m，UP-1 水位孔测点位于上水库库区与下水库库区之间的连接公路旁，测点孔口高程为 738.15 m，通过安装于高程 501.17 m 处的振弦式渗压计对地下水位进行监测。区域范围内布设有 2 和 4# 气象站，用于监测区域范围内的降雨量、温湿度、气压等；同时布设有 1 和 3# 雨量站，仅用于监测区域范围内的降雨量。各测站位于水位测点不同方位，UP-1 水位孔测点及测站具体方位如图 1 所示。

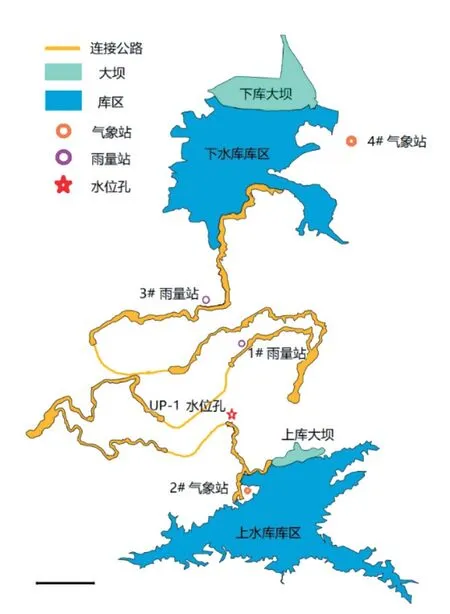
图 1 UP-1 水位孔位置示意图

2.2 影响因素分析

抽水蓄能电站输水系统沿线山体地下水的主要影响因子有大气降水、地表径流、温湿度（蒸发量）、气压等，包气带是地下水与大气水、地表水联系的必经通道。地下水通过包气带获得大气降水和地表水的补给，又通过包气带蒸发与蒸腾排泄到大气圈[6]。大气降水是地下水的主要补给来源，地表水体的部分下渗可以给地下水一定的补给，与气温相关的凝结水亦是地下水的补给来源，该区域范围地下水无人工和其他地表径流等补给。气温与蒸发呈正相关，且是影响凝结水形成的主因；气压与温度呈负相关，相对湿度表征空气的干湿程度及降水条件。故 UP-1 水位孔测点处地下水位变化的主要影响因子选择降雨量、温湿度和气压进行分析。2018 年 10 月—2021 年 4 月 UP-1 水位孔测点水位变化过程线如图 2 所示，测点上下游降雨量和气温监测数据如图 3 所示。

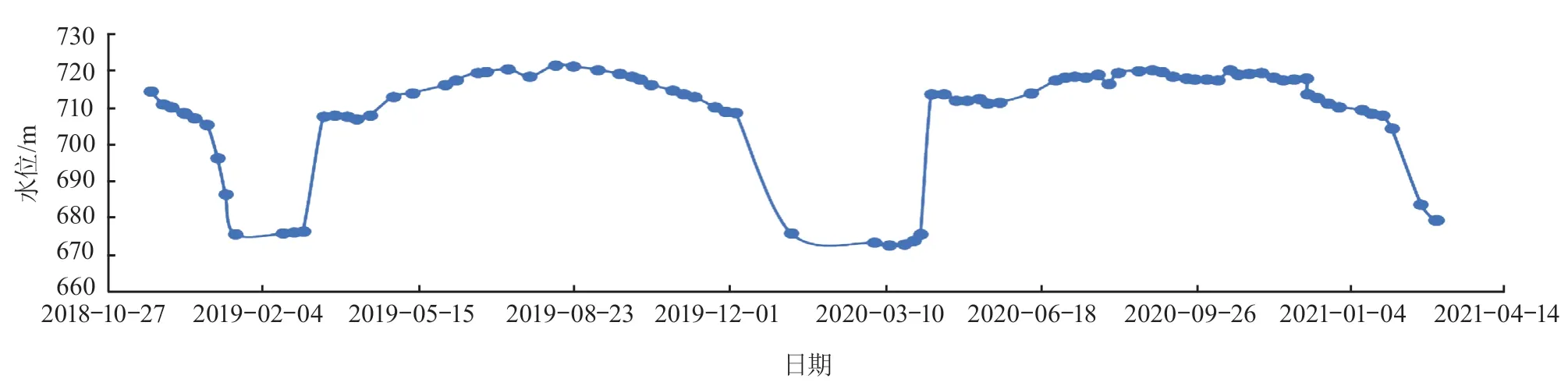
图 2 UP-1 水位孔测点水位变化过程线图

图 3 测点上下游降雨量监测数据图

图 2 和 3 中水位、降雨量、气温历史监测数据显示：每年 3—8 月为降雨量较大月份，该测点处地下水位也呈现上升趋势，在降雨量较小月份水位较低，汛期时水位基本维持 710～720 m，降雨径流入渗会对土壤及地下水位造成影响[7]；2# 气象站环境监测数据显示汛期空气湿度较高，气压较低，与地下水位有相似的变化周期。夏季汛期日均气温上升，日均气压小于冬季，日均空气湿度大于冬季。

2018 年 10 月—2021 年 4 月，地下水位监测间隔时间内气象站的日均气压、湿度、温度与 UP-1水位孔测点地下水位相关系数如表 1 所示。

表 1 环境量与 UP-1 水位孔测点地下水位相关系数

可见地下水位同气温、气压、空气湿度等环境量随季节气候呈周期变化，在不同季节气候内具有一定相关性，其中气温与 UP-1 水位孔测点水位变化呈较强正相关，湿度、气压与水位呈一定负相关。另，地下水位除受到自然因素影响外也会受到人为因素影响[8]。由于地下水位数据采集期间内电站为施工期，因此应排除上、下库区水位对地下水位的影响。

考虑到 UP-1 水位孔上下游有多个气象监测站，而气象监测数据与地下水位数据之间均有一定联系。水位变化除降雨量影响外，也受季节气候等因素影响，呈周期性变化，因此选用电站 2，4# 气象站，以及 1，3# 雨量站监测数据对水位进行预测。

3 模型应用及结果分析

3.1 方法流程

由于气象监测站收集到的环境量数据与地下水位均有一定的相关性，而 PCA 方法可以将影响因子统一进行主成分提取，将原本较多维度的数据在进行降维的同时解决共线性问题，同时 BP 模型可以通过训练不断更新各神经元之间的权值、阈值达到比较理想的预测效果，3 种方法结合优化形成的PCA-GA-BP 模型总流程如图 4 所示。

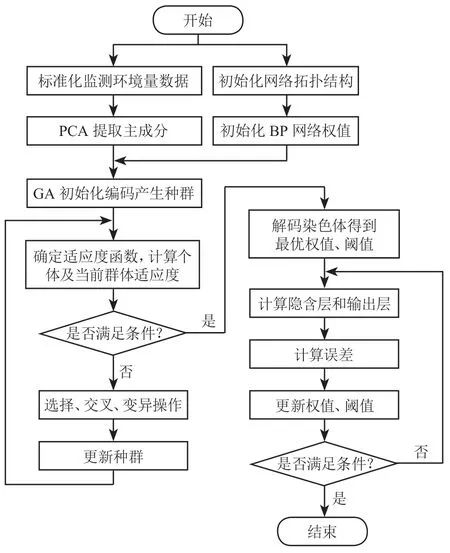
图 4 方法总流程图

本研究选用广东某抽水蓄能电站 2018 年 11 月24 日至 2021 年 2 月 28 日期间内的监测数据。以 1和 3# 雨量站及 2 和 4# 气象站监测得到的对应降雨量X1～X4，2# 气象站测得的气温X5、湿度X6、气压X7，4# 气象站测得的气温X8、湿度X9、气压X10，以及前一次 UP-1 水位孔测点观测水位X11共 11 类监测数据作为模型输入变量，Y1为本次实测水位。X1～X10均为水位测值间隔周期的日平均值，共计 66 组数据，随机选取 50 组用于神经网络训练，剩余 16 组用于测试训练结果，构成模型的训练样本集。

3.2 模型应用

多个监测数据之间具有不同的数量级和量纲，因此需要对数据进行标准化处理，公式如下：

式中：Xi j为原始变量；Mj与Sj分别为第j个变量的均值与标准差；X′i j为原样本标准化后的新样本。

处理后得到X={X1，X2，…，X11}，此时数据样本间均值为 0，方差为 1，使得数据标准统一，提高了数据的可比性。将其通过主成分分析，确定的主成分及贡献率统计如表 2 所示。

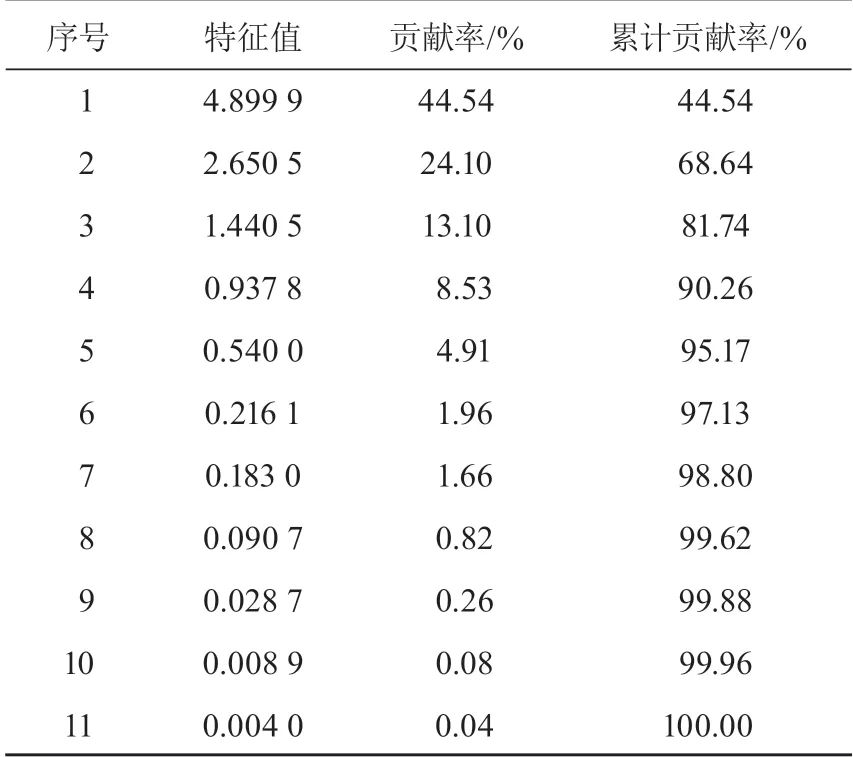
表 2 主成分及贡献率统计表

前 4 个主成分的累计贡献率达到 90.26%，由主成分分析定义，可以选用前 4 个主成分基本代表原始数据信息。BP 神经网络输入层经主成分分析，提取 4 个主成分Z1，Z2，Z3，Z4作为神经网络的输入，因此设定输入层、输出层神经元个数分别为 4和 1 个，即为 UP-1 水位孔测点预测水位。依据以下经验公式确定隐含层神经元的个数[9]：

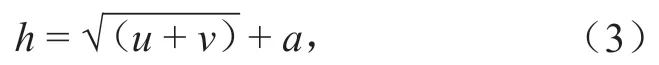
式中：h为隐含层神经元个数；u，v分别为输入和输出层的神经元个数；a为 [1，10] 的调节常数。

对隐含层节点数量调试训练后，最终采用 4-10-1 的网络拓扑结构。但不恰当的学习率和目标误差可能会造成过拟合或达不到预期预测效果，因此通过多次训练调试，设置如下：设置学习率为 0.1，目标误差为 0.000 1；设定隐含层传递函数为 logsig，训练函数为 trainlm（Levenberg-Marquardt 方法），输出层传递函数为 tansig，训练次数为 200 次。遗传算法用以优化神经网络参数（权值w、阈值b），对网络初始参数进行寻优，基本参数选择如下：种群规模为 10 个，最大进化代数为 30 代，交叉概率为0.2，变异概率为 0.15。在保证 GA 计算速度的同时可以得到更佳的适应度，适应度函数设置为均方误差MSE：

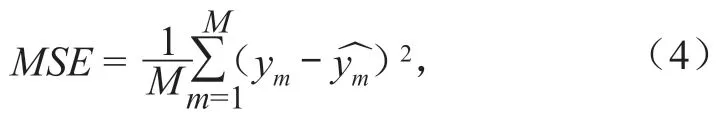
式中：M为样本总数；与ym分别为第m个实际观测值与模型输出值。

参数、函数设置后对网络进行训练及仿真预测，适应度进化曲线如图 5 所示，遗传算法种群在进化至 9 代后最佳适应度已无变化，达到最小值，得到的最优染色体解码后带入神经网络进行模型训练。

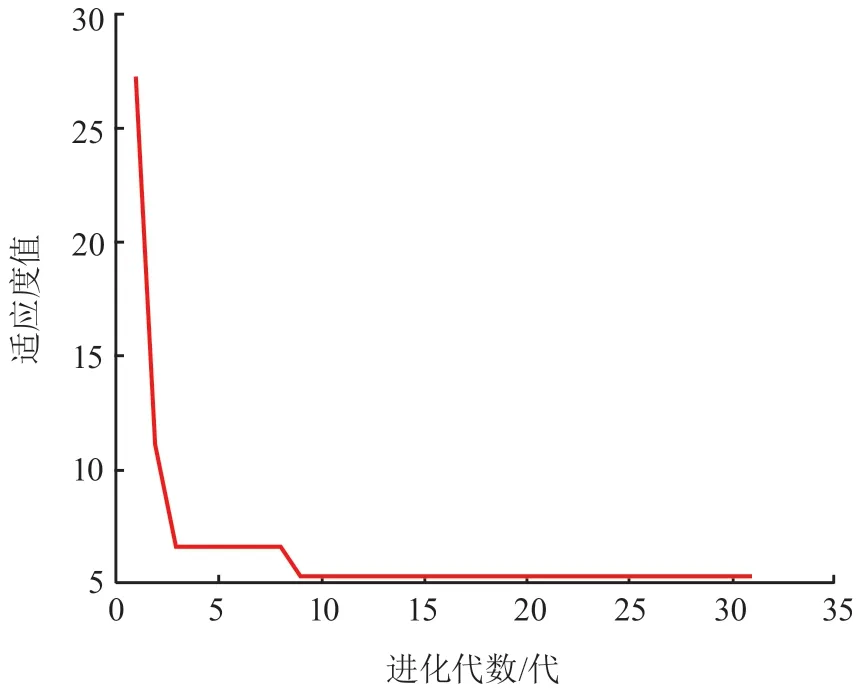
图 5 遗传算法适应度进化曲线（终止代数为 30 代）

同时对 PCA-BP 模型与无优化的 BP 模型进行预测对比，单独的 BP 模型中网络拓扑结构为11-15-1。以相对误差及决定系数R2对模型的预测结果好坏进行评价，公式如下：

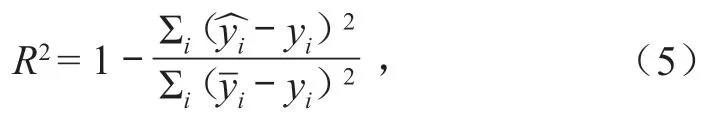
式中：为预测值；yi为真实值；是真实值的均值。

R2的值越接近 1，表明预测结果越好。

3.3 结果分析

16 组测试集预测结果如图 6 所示。

图 6 预测水位与人工测值对比

图 6 中实测水位为人工测值，实际应用中使用全站仪及电测水位计对实际水位进行测读，误差在±1 cm 以内。随机选取的测试样本中有 3 组为较低水位，预测结果与人工测值误差均不大，PCA-GABP 模型的R2为 0.968，相较于 PCA-BP 与 BP 模型的 0.945 和 0.943，拥有更高预测精度。由图 6 可知三者的预测结果与实测值基本吻合，在水位的高、低上预测基本无误。不同水位下模型平均绝对误差对比如表 3 所示。

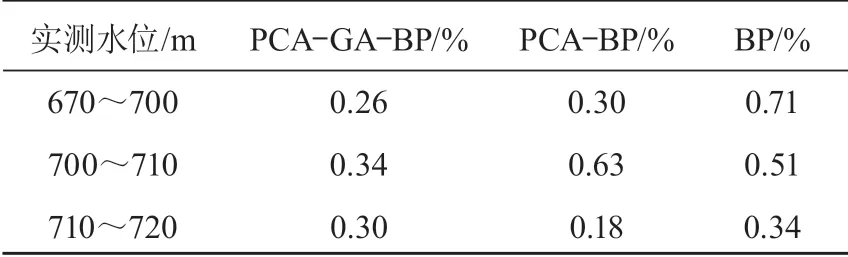
表 3 不同水位下模型平均绝对误差对比

在 670～700 m 实测水位中，对比 PCA-BP 与BP模型，PCA-GA-BP 模型平均绝对误差分别减小0.04%，0.45%；GA-BP 模型在 710～720 m 水位预测中表现较好，但在 700～710 m 水位预测中误差较大；PCA-GA-BP 模型在各水位下拥有更高的综合预测精度，其相对误差最大值小于 PCA-BP 和 BP模型，可见通过 PCA 与 GA 优化了模型整体预测精度。

4 结语

为提高抽水蓄能电站地下水位预测精度，对广东某抽水蓄能电站输水系统沿线山体地下水位具有影响的多个环境量进行了分析，运用了 PCA-GABP 模型通过历史水位及实时环境量对地下水位进行预测。

研究实验表明：地下水位与环境量具有一定的相关性，使用 PCA-GA-BP 模型可以对抽水蓄能电站沿线山体地下水位进行预测。该方法对地下水位预测具有较高精度，R2为 0.968，实例使用了多个与地下水位存在一定相关的环境量作为水位预测输入，通过 PCA 模型简化网络拓扑结构，并在一定程度上解决变量间的共线性问题，相较于未使用 GA方法的单 BP 模型拥有更高的精度，使得 BP 网络拥有更佳的初始权值、阈值，避免网络陷入局部最优等问题。

在水位监测未实现自动化时，由于人工数据采集频次有限，可以通过监测环境量对地下水位进行预测，从而补全水位监测数据，或者在电站蓄水后将不蓄水预测水位数据与蓄水后实测水位进行对比，进而研究大坝蓄水对地下水位的影响。也可在大坝蓄水后单独研究库水位数据，进而研究库水位与沿线山体之间的模型。该模型方法可推广至其他水位孔水位预测，对蓄能电站上、下库输水系统沿线山体边坡的安全评估等领域具有一定实用价值。