基于改进SSD和MOMEDA的滚动轴承复合故障诊断*

2022-06-29刘尚坤范壮壮孔德刚张秀花

组合机床与自动化加工技术 2022年6期

刘尚坤，张伟，范壮壮，孔德刚，张秀花

(河北农业大学机电工程学院，保定 071001)

0 引言

滚动轴承是支撑转轴的关键部件，其运行状态直接影响设备的工作性能和运行安全[1]。恶劣的工作环境等原因常导致轴承发生复合故障，又由于各故障之间相互影响、各故障特征混叠，致使故障特征的准确分离和诊断更加困难[2]。为满足机械装备作业的高安全性和高可靠性要求，开展轴承故障诊断研究意义重大。

复合故障振动信号包含多源信息，通过分解的方式获得各源信息是有效的故障特征提取途径。但现有方法多存在一些不足，如固有时间尺度分解算法会导致分量带有毛刺而失真[3]，辛几何模式分解的分量过多[4]，变分模态分解的分解效果受参数选择影响[5]。BONIZZI等[6]提出了奇异谱分解(singular spectrum decomposition，SSD)新方法，它具有高的分解精度，能有效地抑制模态混叠和伪成分。CHEN等[7]建立了SSD分量的多尺度信息维度特征，并结合卷积神经网络准确识别出实验行星齿轮的退化状态；唐贵基等[8]利用散布熵改进了SSD，有效提取出齿轮故障特征信息；但这些关于SSD的研究均是在单一故障诊断中的分析应用，在轴承复合故障中的应用有待进一步研究，同时需要解决SSD分解层数需凭经验设定问题。

滚动轴承常见于内圈、外圈、滚动体和保持架故障，不同故障有相应的故障频率，而复合故障诊断的关键是分离各故障的周期性冲击特征[9]。为此，本文将SSD引入到轴承复合故障诊断中，以不同故障周期的相关峭度值最大化为目标，通过相关峭度图方式，改进SSD分解层数需凭经验设定难以选到最优分量的缺点，实现不同故障特征的初步分离；再利用多点最优最小熵解卷积调整(multipoint optimal minimum entropy deconvolution adjusted，MOMEDA)方法能够降低非故障成分影响、突出故障冲击特征的优点[10]进行降噪、去除干扰后处理。因此，提出基于改进SSD和MOMEDA的滚动轴承复合故障分离诊断方法。实验信号分析结果表明不同故障需要各自的最优分解层数、验证了该方法的有效性。

1 基本理论

1.1 奇异谱分解

SSD能够将时域振动信号分解为一系列不同固有时间尺度的奇异谱分量(singular spectrum component，SSC)，SSD的基本过程如下：

(2)自适应选取嵌入维数M。由式(1)计算第j次迭代时残余分量vj(n)的功率谱密度：

(1)

估算vj(n)的PSD最大峰值对应的频率fmax，若首次迭代后归一化频率fmax/fs小于设定的阈值10-3(fs为采样频率)，则认为其是大趋势项，M设定为N/3；当j>1时，M=1.2×(fmax/fs)。

(2)

当该值小于阈值0.01时，终止迭代；否则，残余量继续迭代，直到满足停止条件，最后分解结果如式(3)所示。

(3)

式中，m为奇异谱分量个数；v(m+1)(n)为残余量。

1.2 改进SSD

相关峭度(correlation kurtosis，CK)充分考虑了冲击成分的连续性，避免了峭度易受异常突出脉冲干扰，相关峭度因为能够检测所关注的故障周期，能检测信号中不同周期成分[11]，相关峭度的计算式为：

(4)

式中，T为相关故障周期；N为信号的采样点数；M为移位数。

因此，本文以相关峭度作为复合故障的分离指标，利用相关峭度图方式，改进SSD分解分解层数需要凭经验设定的不足，同时解决最优分量的选取问题，思路如下：

(1)通过SSD方法分别将原始振动信号分解成第k层k个分量(2≤k≤K，K为分解层数上限，本文取8)。

(2)根据轴承复合故障中不同故障特征频率确定各相应的故障采样点周期Tfault，计算每层分解后的k个分量与各Tfault的相关峭度值。

(3)分别用每层k个分量序号、分解层数和各故障的相关峭度值，构造相关峭度图，从图中选定相关峭度值最大的分解层数和最优分量，实现改进SSD功能、初步分离各故障。

1.3 MOMEDA

多点最优最小熵解卷积调整(MOMEDA)克服了MED易受尖脉冲影响、MCKD参数过多的缺陷，将连续周期脉冲序列作为解卷积目标，运用非迭代解卷积方式选取全局最优滤波器，其目标函数为：

(5)

式中，T为故障周期；f为滤波器组向量。目标向量t定义了解卷积目标冲击成分的位置和权重。当目标向量t与原冲击信号y契合时，解卷积效果达到最佳。

对式(5)求逆滤波器系数f的导数：

(6)

再求其极值：

(7)

(8)

取其特解作为一组最优滤波器，记为：

(9)

2 基于改进SSD和MOMEDA的复合故障分离诊断方法

为准确分离噪声环境下滚动轴承的复合故障，本文利用改进SSD方法，以相关峭度图方式表征轴承不同故障周期相关峭度值，优选出不同故障各自最优分解层数及最优分量，再结合MOMEDA消除故障特征间交叉影响及噪声等干扰、增强冲击特性的优点，最后通过包络分析实现各故障的分离诊断，具体流程如图1所示。

图1 基于改进SSD和MOMEDA的复合故障分离诊断流程

3 实验分析

为了验证所提方法的有效性，在QPZZ-Ⅱ型轴承实验平台上开展轴承内、外圈复合故障实验，实验台结构如图2a所示。轴承型号为6205E，内圈和外圈滚道上各加工宽0.2 mm的沟槽，如图2b所示，模拟轴承复合故障。实验中，外圈故障位于12点方向以模拟弱故障冲击，电机转速为1466 r/min，采样频率为12 800 Hz。实验轴承的结构参数和计算该轴承的故障特征频率分别如表1和表2所示。

表1 滚动轴承结构参数

表2 故障特征频率

(a) 实验平台 (b) 复合故障轴承

传感器拾取的振动信号时域波形及其包络谱如图3所示，包络谱中内圈故障特征频率fi及其倍频突出体现，同时存在低幅值外圈故障特征频率fo，并且存在噪声等其他干扰成分，各故障特征不能分离。

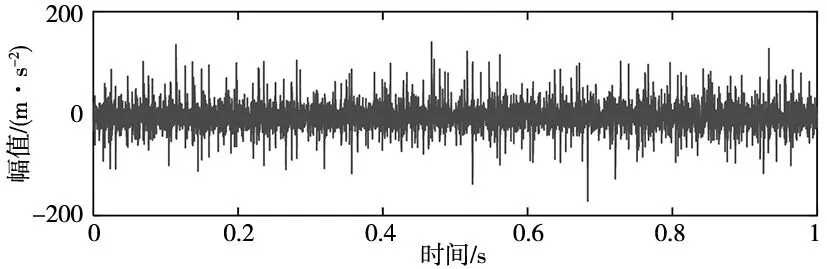
(a) 时域图

利用本文所提出方法对实验复合故障信号进行分析，先用SSD将信号依次分解为2～8个分量，由Tfault=fs/ffault分别计算出内、外圈故障频率fi、fo的对应故障采样点周期Ti=96.7、To=146.0，然后分别计算每次分解中各分量对内、外圈故障周期的相关峭度，分别画出内、外圈的相关峭度图如图4a和图4b所示，由图4a可知，Ti相关峭度值最大时，最优分解层数为5，最优分量为SSC2；由图4b可知，To相关峭度值最大时，最优分解层数为7，最优分解分量为SSC5。

(a) 内圈Ti的相关峭度图 (b) 外圈To的相关峭度图

实验信号内、外圈最优分量时域波形及包络谱分别如图5和图6所示。图5b内圈SSC2的包络谱中，虽然内圈故障频率fi及其倍频明显，但同时存在小幅值外圈故障频率并夹杂少量干扰频率；图6b外圈SSC5的包络谱中，外圈故障频率fo及2、3倍频明显，同时存在小幅值内圈故障频率和干扰频率。虽然基本实现了轴承内、外圈复合故障的分离，但存在交叉及干扰频率。

(a) SSC2时域图

(a) SSC5时域图

为了削弱内、外圈故障最优分量中的交叉项及干扰频率成分，再分别利用MOMEDA对各最优分量进行降噪和增强故障冲击处理，结果如图7和图8所示，分别与图5和图6对比可知，包络谱中交叉项及干扰频率得到抑制、冲击故障周期均得以增强。在图7b中内圈故障特征频率fi～4fi清晰可见，且无干扰成分；在图8b中外圈故障特征频率fo～6fo幅值更加突出，能够实现轴承内、外圈复合故障的准确分离和诊断。

(a) 时域图

为了对比，下面采用快速谱峭度法对实验信号进行分析，结果如图9所示。图9a出现了两个较为明显的共振频带，频带1的中心频率为2400 Hz，频带2的中心频率为5 066.7 Hz，带宽均为533.3 Hz；分别对两个频带滤波后的信号做包络分析如图9b和图9c所示，可知，虽然内圈故障特征频率fi～3fi和外圈故障特征频率fo～3fo被基本分离开来，但图9b外圈故障频率中有交叉项内圈故障特征频率，同时两个包络谱中都伴有较多干扰频率成分。对比结果表明，快速谱峭度不如本文方法得到的包络谱清晰，不利于准确的分离和诊断复合故障类型。