基于Actor-Critic算法的多无人机协同空战目标重分配方法

陈宇轩，王国强*，罗 贺，马滢滢

(1.合肥工业大学 管理学院，安徽 合肥 230009；2.过程优化与智能决策教育部重点实验室，安徽 合肥 230009；3.智能互联系统安徽省实验室，安徽 合肥 230009)

0 引言

随着无人化、自动化和人工智能等技术的飞速发展，现代空战无人机间的交互需求不断提高，多无人机协同作战逐渐成为空战的主要形式[1-2]。无人机间通过自主协同，将单个无人机优势转化为编队的整体优势，实现“1+1>2”的空中作战效果[3]。多无人机协同目标分配能够利用分散的单机作战资源，合理有序地分配目标进行打击，是提升打击效能与作战能力的有效途径之一[4]。

近年来，大量学者主要对空战中给定双方态势下的静态目标分配问题展开研究[5-14]，仅考虑单次目标分配，然而真实空战瞬息万变，作战前的目标分配方案可能随着对抗时间的进行而不再适用当前环境，对此，决策者需要根据复杂、动态变化的战场环境找准改变当前决策的关键时机，及时更改初始决策以达到整体作战收益最大或作战代价最小的目的。因此，有效的目标重分配将成为对抗过程中改变局势、由劣转优和有效增强我方优势的重大举措。

目前，针对空战过程中目标重分配问题的研究文献较少。其中，龚阳等[15]将目标数量变化作为决策触发依据，并采用高斯分量权值方法进行目标重分配；张阳等[16]和刘振等[17]通过设计简单的规则得到决策触发时机，并运用基于协议规则的算法模拟无人机目标分配；杨尚君等[18]同时考虑固定周期和突发事件作为重分配触发规则，并采用混合细菌觅食算法进行任务重分配。综上，当前对于多无人机协同目标重分配的研究多注重于重决策结果本身，而决策触发时机的选取大多都是基于规则或通过阈值来设定的，这类方法原理简单、易于实现，但忽视了空战场景中的对抗性。同时，在这种不确定信息下的求解存在搜索空间大、参数变化大等特点，用常规算法求解具有很大的局限性，这就对目标重分配触发时机的求解方法与求解质量提出了更高的要求。

随着人工智能技术的飞速发展，深度学习和强化学习在智能决策方面取得了重大突破。目前，在重部署[19]、重调度[20]和重规划[21-22]等方面均有大量的研究。这些研究对本文以强化学习方法求解目标重分配问题具有一定的启发。基于上述分析，首先定义了多无人机协同空战目标重分配问题，并建立了多无人机协同空战目标重分配总体框架，以所有无人机的状态信息作为输入得到目标重分配时机；然后，针对稀疏奖励难题，结合双方无人机态势优势，设计了双层奖励回报方法，加快策略网络收敛速度；最后，基于VR-Forces的多无人机协同空战仿真平台，验证了本文方法的有效性。

1 问题描述

本文研究的多无人机协同空战目标重分配问题可以描述为：在超视距环境中，红方无人机探测到蓝方无人机，并根据空战态势优势、自身作战能力以及对手能力威胁等因素，判断出需要重决策的关键时刻T，在T时刻进行目标重分配，每架无人机按照目标重分配方案向新目标飞行并进行后续对抗，从而在对抗过程中占据优势，重复上述过程直至对抗结束。

多无人机目标重分配过程如图1所示。环境中包括红方无人机和蓝方无人机，其中，T时刻红方无人机根据敌我双方的态势信息判断是否触发目标重分配。

图1 多无人机目标重分配过程Fig.1 Multi UAV target re-assignment process

假定红方无人机数量为M，蓝方无人机数量为N，每架无人机搭载的武器数量为Z，z∈Z，最大探测距离为DRmax，最大攻击距离为DMmax，且每枚导弹对目标的毁伤概率已知，当无人机的探测范围内出现对方无人机时，进行首次目标分配，目标分配后无人机会向被分配的目标方向飞行，设DRiBj表示红方i无人机与蓝方j无人机之间的距离，满足DRiBj≤DMmax时，发射一枚导弹，每个无人机执行目标分配方案时只能攻击一个目标，当z=0时，不再执行目标分配方案。

设红方的目标重分配的触发结果为at∈{0,1}，其中，at=0表示红方无人机在t时刻不改变当前目标分配方案，at=1表示红方无人机在t时刻进行目标重分配，目标重分配结果包括以下4种：

① 红方1号无人机攻击蓝方1号无人机，红方2号无人机攻击蓝方1号无人机；

② 红方1号无人机攻击蓝方2号无人机，红方2号无人机攻击蓝方1号无人机；

③ 红方1号无人机攻击蓝方1号无人机，红方2号无人机攻击蓝方2号无人机；

④ 红方1号无人机攻击蓝方2号无人机，红方2号无人机攻击蓝方2号无人机。

无人机状态示意图如图2所示。对于对抗过程中的每一个无人机，可获取到的状态参数用X表示，X=(x,y,z,v,θ,φ)，其中，(x,y,z)表示无人机的三维坐标，v表示无人机的速度，θ表示无人机的俯仰角，φ表示无人机的航向角。

图2 无人机状态示意Fig.2 Schematic diagram of UAV status

以最大化摧毁蓝方目标数量和最小化红方损失作为目标函数，则目标函数F为：

F=max(∑nj-∑mi),nj∈{0,1}，mi∈{0,1}

i=1,2,…,M，j=1,2,…,N，

(1)

式中，nj=1表示蓝方无人机j被摧毁，nj=0表示蓝方无人机j存活；mi=1表示红方无人机i被摧毁，mi=0表示红方无人机i存活。

2 求解方法

2.1 总体框架

多无人机协同空战目标重分配方法的总体框架如图3所示。

图3 多无人机目标重分配总体框架Fig.3 General framework of multi-UAV target re-assignment

该框架包含多无人机协同目标重分配过程和Actor-Critic强化学习框架2大部分，其中，多无人机协同目标重分配全过程表示：设计出一个目标重分配触发机制，通过无人机传感器获取到的信息，实时解算出目标重分配的触发时刻T，并在时刻T通过调用现有目标分配模块的方式求解目标分配方案，最后根据更新后的目标分配方案进行后续对抗。Actor-Critic强化学习框架表示：智能体根据环境得到状态信息s，s∈S，输入到Actor网络中求解出相应动作a，a∈A，环境会根据输出的动作产生改变，并计算出一个奖励回报R反馈给Critic网络，同时，Critic网络会根据环境给予的奖励回报R计算TD误差修正Critic网络和Actor网络，最后不断循环以上过程。综上，本文采用训练好的Actor网络作为目标重分配触发机制来解决多无人机协同空战目标重分配问题。因此，结合Actor-Critic框架对多无人机协同空战目标重分配过程构建马尔科夫决策过程(MDP)。

MDP简单说就是一个智能体(agent)采取行动(action)从而改变自己的状态(state)获得奖励(reward)与环境(environment)发生交互的循环过程。可以由公式M=表示：

①S：有限状态集合，为双方所有无人机的状态数据X=(x,y,z,v,θ,φ)，包括4架无人机的位置坐标(x,y,z)，俯仰角θ，航向角φ和速度v等参数，共24维输入数据；

②A：有限动作集合，目标重分配的触发结果at∈{0,1}，触发结果包括目标分配at=1和维持不变at=0两种，共2维输出数据；当触发结果为目标分配时，无人机会根据新的目标分配结果，朝目标飞机方向飞行，当目标达到我方无人机的攻击范围内时发射一枚空空导弹；

③T(S,a,S′)～Pr(s′|s,a)：根据当前状态s和动作a预测下一个状态s′，Pr表示从状态s采取行动a转移到s′的概率；

④ 奖励回报R：R(s,a)=E[Rt+1|s,a]，表示agent采取某个动作后的即时奖励。

采用强化学习方法进行学习的过程就是使获得累计奖励回报最大化的过程，即：

(2)

多无人机协同空战目标重分配方法的运行过程伪代码如下：

2.2 网络结构

基于2.1节多无人机协同空战目标重分配方法的总体框架，下面对总体框架中的Critic网络和Actor网络进行详细设计。

2.2.1 Critic网络

在多无人机协同空战的过程中，Critic网络输入的是双方无人机的状态信息，输出为对当前局势的评判值，即状态值函数。神经网络可以对非线性函数无限逼近，因此，建立了一个多层神经网络来拟合状态值函数。通过Critic网络分别计算当前的状态值函数V(st)=E[Rt+1+γV(St+1)|St=s]和下一时刻的状态值函数V(st+1)，同时计算二者间的时间差分误差(TD误差)，得到Loss函数，最后采用函数优化器更新Critic网络参数，即：

FLoss=V(st)φ(t)，

(3)

w′←w+β·FLoss，

(4)

式中，β为Critic网络学习率；φ(t)为TD误差，计算公式为：

φ(t)=rt+1+γV(st+1)-V(st)。

(5)

为了拟合状态值函数，采用含有2层隐藏层的全连接神经网络，隐藏层神经元取25，激活函数采用Relu函数，如图4所示。通过随机梯度下降优化损失函数，更新网络参数。

图4 Critic网络设计Fig.4 Critic network design

2.2.2 Actor网络

在多无人机协同空战的过程中，Actor网络输入的是双方无人机的状态信息，输出目标重分配的触发结果。用参数化的行为策略Pθ表示红方无人机选择的动作，θ是策略的参数，即Pθ(s|a)表示在策略θ参数下，红方无人机处于状态s执行动作a的概率。同时结合在Critic网络得到的TD误差φ(t)计算Loss函数值，进而更新Actor网络参数，即：

θ′←θ+α·(rt+1+γVπ(st+1)-Vπ(st))lnPθ(at|st)。

(6)

Actor网络结构如图5所示，与Critic网络结构相似，采用含有2层隐藏层的全连接神经网络，隐藏层神经元取25，隐藏层激活函数采用Relu函数，输出层激活函数采用softmax函数，通过随机梯度下降优化损失函数，更新网络参数。

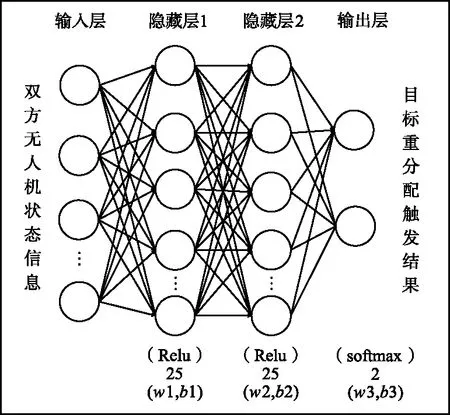
图5 Actor网络设计Fig.5 Actor network design

2.3 奖励回报

在多无人机协同空战的场景下，采用强化学习方法往往存在稀疏奖励问题，仅有对抗双方无人机的损毁才可以得到明确的奖励，对抗中不能立刻得到客观的回报，这就导致奖励回报难以人为设计且存在主观性和经验性，进而影响模型的训练效率。因此，针对此问题，设计了全局和局部2部分相结合的双层奖励回报，如图6所示。

图6 奖励回报设计思路Fig.6 Reward design ideas

本文奖励回报的设计遵循以下2个原则：

① 以最大化摧毁蓝方无人机数量和最小化红方损失作为主要目标。

② 红方在对抗过程中尽量增大对抗优势。

因此，奖励回报的设计主要考虑无人机存活情况以及态势优势，设计如下所示：

r=r0+r1，

(7)

式中，r为奖励回报；r0为全局奖励回报；r1为局部奖励回报。

(1) 全局奖励回报

全局奖励回报具体设计如下：

r0=k*(N-p)+(-k)*(M-q)，

(8)

式(8)表示当发生蓝方无人机损毁时，获得k奖励回报；同理，发生红方无人机损毁，获得-k奖励回报。r0为全局奖励回报；M为红方无人机初始数量；N为蓝方无人机初始数量；q为红方无人机存活数量；p为蓝方无人机存活数量。

(2) 局部奖励回报

局部奖励回报又称引导型奖励回报，由距离奖励回报、角度奖励回报以及速度奖励回报3部分组成，具体设计如下：

r1=r11+r12+r13，

(9)

式中，r1为局部奖励回报；r11为距离奖励回报；r12为角度奖励回报；r13为速度奖励回报。

① 距离奖励回报r11

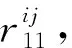
(10)

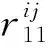
(11)

(12)

式中，DRmax为最大搜索距离；DMmax为最大攻击距离；DRiBj为红方无人机i到蓝方无人机j的距离；DLmax为红方无人机i与蓝方无人机j的初始距离；m为距离系数。

② 角度奖励回报r12

(13)

(14)

③ 速度奖励回报r13

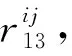
(15)

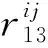
(16)

(17)

式中，v0为最佳攻击速度；vRi为红方无人机i速度；vBj为蓝方无人机j速度；vmax为无人机最大速度。

3 实验分析

基于多无人机协同空战目标重分配问题的典型案例，详细说明了验证本文方法的仿真环境；对所提出方法进行参数敏感性分析，分析本文方法的最优超参数；针对所设计的奖励回报，分析出超参数k的最佳取值；在多种典型对抗场景进行仿真实验，分析方法有效性；针对本文所设计的全局奖励回报和局部奖励回报，设计消融实验，分别研究全局奖励回报和局部奖励回报对算法性能的影响。

3.1 实验环境与实验设定

3.1.1 基于VR-Forces开发的仿真环境

本文基于VR-Forces环境搭建了多无人机协同空战目标分配仿真平台[28]，该平台由红方子系统、蓝方子系统、白方子系统以及强化学习算法子系统4部分组成，并在同一局域网下进行通信。

多无人机协同对抗仿真系统如图7所示。该仿真系统包括红方子系统、白方子系统、蓝方子系统和目标分配子系统，采用分布式架构部署在4台机器上，红方加载本文方法与蓝方基线触发规则进行对抗，同时红蓝双方均布有目标分配算法，白方通过加载批处理模块和数据记录模块进行训练和结果显示。

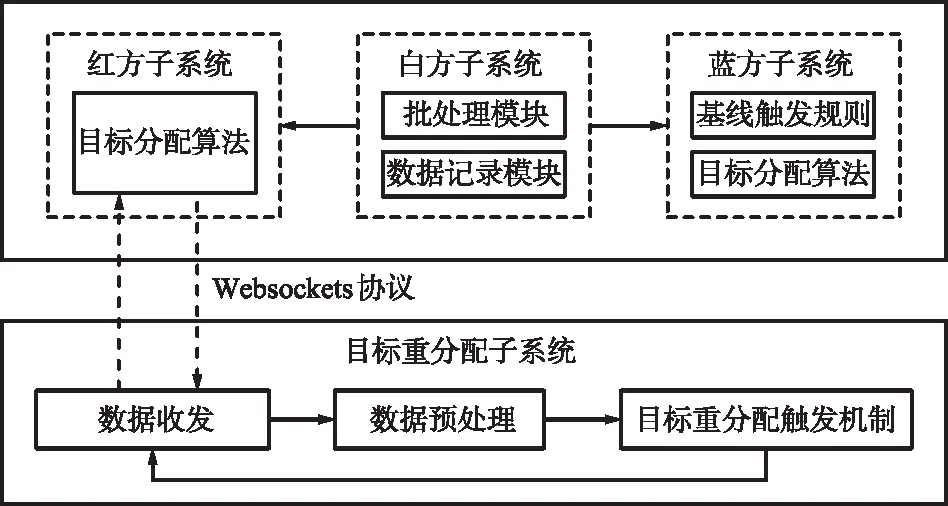
图7 多无人机协同对抗仿真系统Fig.7 Multi-UAV cooperative confrontation simulation system

其中，红方子系统作为客户端，目标重分配子系统作为服务端，通过采用websockets协议实现子系统间的通信，进行数据的交互，发送的数据使用json格式进行封装。目标重分配子系统接收到数据后，需要进行数据转换、数据补全和数据归一化等预处理再输入到算法中进行仿真训练。仿真系统的软硬件参数如表1所示，目标重分配触发机制参数如表2所示。

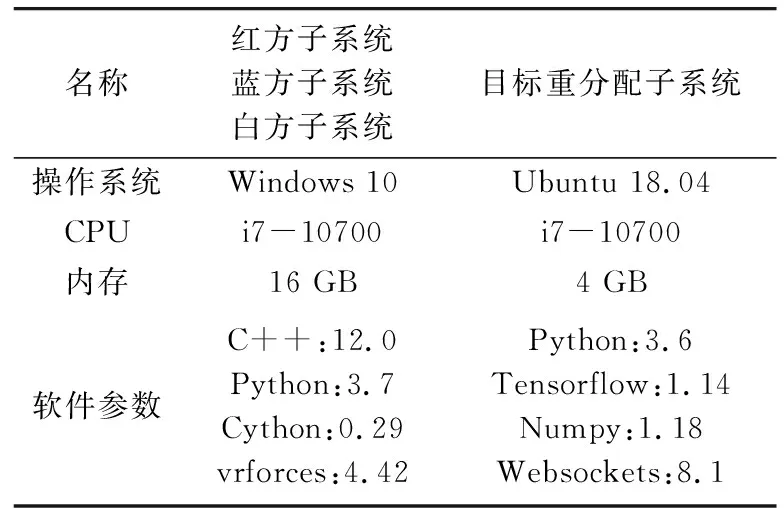
表1 软硬件环境参数Tab.1 Software and hardware environment parameters

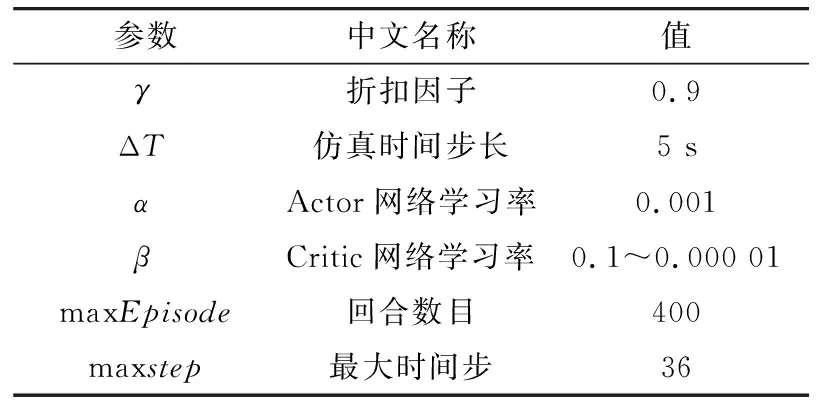
表2 目标重分配触发机制参数Tab.2 Target re-assignment trigger mechanism parameters

3.1.2 实验场景介绍

2对2典型对抗场景示意图如图8所示。仿真对抗区域为50 km×80 km的矩形区域，共有4架无人机，其中2架蓝方无人机，2架红方无人机，每个无人机的武器数量为4个，每个无人机具有相同的毁伤概率，对抗仿真时长取3 min为一局。

图8 2对2典型对抗场景示意Fig.8 Schematic diagram of 2V2 typical confrontation scenario

(1) 评价指标定义

在仿真单局对抗结束时，根据对抗双方无人机的剩余数量，定义了3种仿真实验结果，具体如下：

① 红方获胜：单局仿真结束时，红方剩余的无人机数量多于蓝方；

② 红方平局：单局仿真结束时，红方和蓝方剩余的无人机数量相同；

③ 红方失败：单局仿真结束时，红方剩余的无人机数量少于蓝方。

在分析仿真对抗胜率变化时，采用Li等[25]提出的获胜率和失败率，具体计算如下：

对抗胜率 = 胜场 /(胜场 + 败场)×100%，

失败率 = 败场 /(胜场 + 败场)×100%。

(2) 典型对抗场景设计

在多无人机协同对抗过程中，对抗双方之间的优劣势主要和对抗双方无人机的数量、性能以及相对态势有关。当双方无人机的数量、性能相同时，对抗双方之间的优劣势主要和双方无人机的相对态势有关[26-27]。对此，通过调整对抗双方无人机的位置、角度，分别设计了红方优势、红方劣势和双方均势情形下的典型对抗场景。

(3) 基线触发规则

参考张阳等[16]设定的决策触发规则作为目标重分配基线触发规则，包括：

① 当双方无人机数量变化；

② 当对方无人机进入探测范围。

(4) 目标分配算法

进行仿真实验时，双方无人机的目标分配算法均采用马滢滢等[4]提出的基于混合整数规划转换的双矩阵博弈目标分配算法。

(5) 实验组与对照组

在同一典型对抗场景下分别进行实验组和对照组2类实验，通过对比多个典型对抗场景下实验组和对照组的数据进行实验分析。

① 实验组

红方：基于Actor-Critic算法的多无人机协同空战目标重分配方法，目标分配算法；

蓝方：基线触发规则，目标分配算法。

② 对照组

红方：基线触发规则，目标分配算法；

蓝方：基线触发规则，目标分配算法。

3.2 参数敏感性分析

在参数敏感性分析实验中，通过调整Critic网络学习率β，比较在同一场景下对抗的获胜场次、平局场次和失败场次，分析出学习率变化对仿真对抗的影响。只需要改变Critic网络学习率就可以调整网络的更新幅度，因此无需对Actor网络参数进行敏感性分析。

学习率分别取10-1，10-2，10-3，10-4和10-5，并在不同场景下进行400场仿真对抗，不同学习率下的实验结果如表3所示。

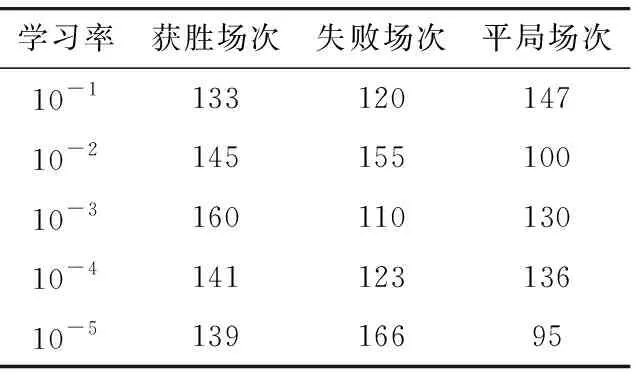
表3 参数敏感性分析仿真实验结果Tab.3 Experimental results of parameter sensitivity analysis

由表3可知，在获胜场次上，当学习率取10-3时，获胜场次最高160场，其次是学习率取10-2，10-4时，获胜场次高于140场；在失败场次上，当学习率取10-3时，失败场次最少，为110场，其次是学习率取10-1，10-4时，失败场次低于130场。因此，在参数敏感性分析实验中，学习率的最佳取值为10-3。

3.3 奖励回报设计实验

在奖励回报设计实验中，通过改变全局奖励回报超参数k，来调整全局奖励回报和局部奖励回报间的占比关系，从而分析奖励回报取值变化对对抗胜率的影响，超参数k分别取1，3，5，7和9，并进行400场仿真对抗，不同全局奖励回报超参数k下的对抗胜率如图9所示。

由图9可知，当超参数k=1，k=3和k=5时，对抗胜率随着场数的增加而增加，k=5时对抗胜率增长幅度最大，k=1时对抗胜率增长幅度最小，由此可见，当k=1和k=3时，由于全局奖励回报的占比过少，导致对抗胜率增长缓慢；当超参数k=7时，在001～100场、101～200场的训练中，对抗胜率最高、提升的最快，然而，在201～300场的训练中发生了大幅度的下降，由此可见，全局奖励回报的占比过高时，淡化了局部奖励回报的作用，造成了训练的不稳定；超参数k=9时，在101～200场的训练中发生了大幅度的下降，后续对抗胜率持续升高，最终略高于k=3和k=7时的对抗胜率。综上，当k=5时训练可以稳定提升对抗胜率，因此，在后续实验中超参数k=5。

3.4 方法有效性实验

为了本文方法的有效性，在每个场景下分别做400次仿真对抗实验，与对照组实验进行对比，分析该方法的有效性。均势场景下对抗结果如图10所示，优势场景下对抗结果如图11所示，劣势场景下对抗结果如图12所示。

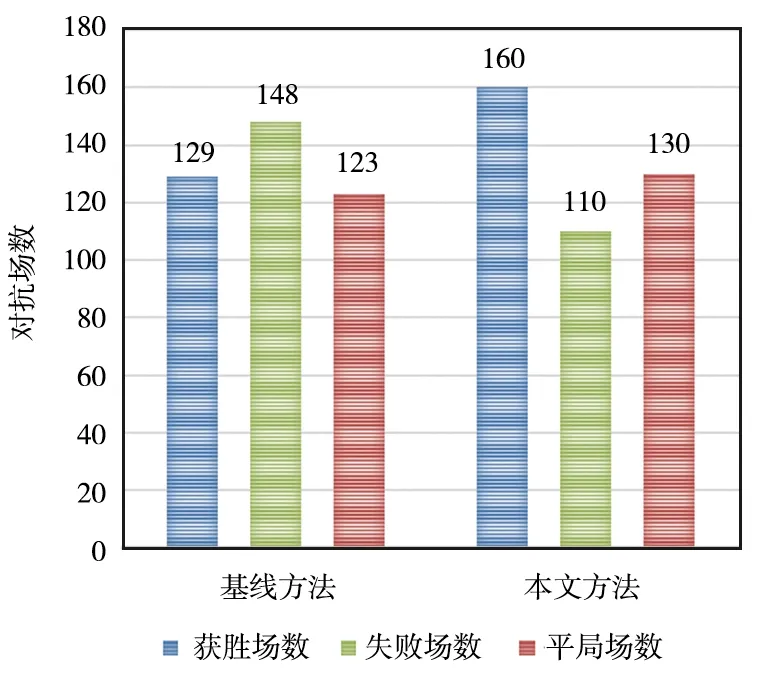
图10 均势场景下对抗结果Fig.10 Confrontation results under power-balanced scenarios

图11 优势场景下对抗结果Fig.11 Confrontation results under advantageous scenario

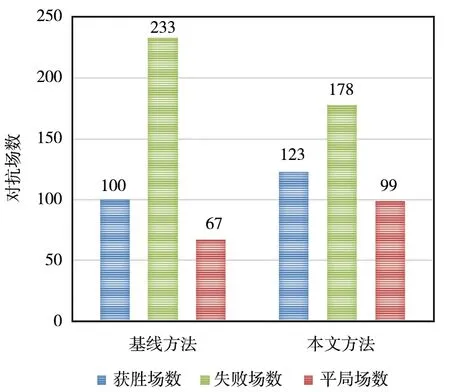
图12 劣势场景下对抗结果Fig.12 Confrontation results under disadvantageous scenario

从实验可以看出，在3种典型对抗场景下，采用本文方法的效果均不同程度地优于基线方法。由图10可以看出，在均势场景中采用本文方法，平局场数增加7局，失败场数降低38局，获胜场次增加31局；由图11可以看出，优势场景中实验组比对照组的获胜场次增加39局，失败场次减少6局，可以看出在优势场景下采用本文方法可以增大优势，对抗胜率；由图12可以看出，劣势场景中实验组比对照组的获胜场次增加23局，失败场次减少55局，可以看出在劣势场景下采用本文方法可以改变劣势，从而提高胜率。

在3种不同的典型对抗场景下的胜率变化如图13、图14和图15所示。

图13 均势场景下胜率变化Fig.13 Change of winning rate under power-balanced scenario

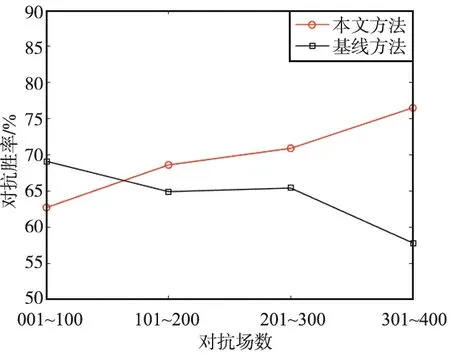
图14 优势场景下胜率变化Fig.14 Change of winning rate under advantageous scenario

图15 劣势场景下胜率变化Fig.15 Change of winning rate under disadvantageous scenario

由图13可以看出，在均势场景中采用本文方法，对抗胜率持续上升，与训练次数成正比关系。同时，由图14和图15可以看出，在优势场景、劣势场景下对抗胜率随训练次数的增加均有不同程度的上升。综上可见，本文所提出的多无人机协同空战目标重分配方法能够有效地提升空战对抗的胜率。

3.5 消融实验

本文所设计的奖励回报包含全局奖励回报和局部奖励回报2部分，为分析全局奖励回报和局部奖励回报对算法性能的影响，设计消融实验，实验设置如表4所示。

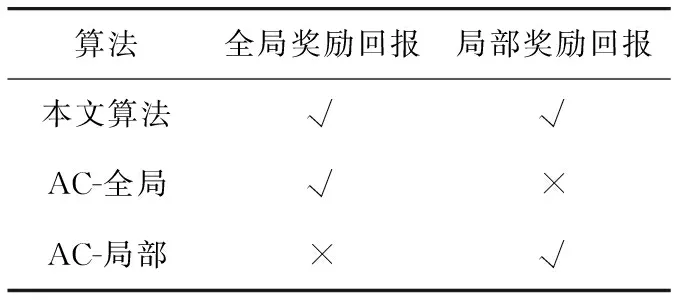
表4 消融实验设置Tab.4 Setting of ablation experiment

其中，AC-全局表示仅包含全局奖励回报；AC-局部表示仅包含局部奖励回报。本文算法、AC-全局和AC-局部算法随着对抗场数的增加，对抗胜率的变化情况如图16所示。

图16 消融实验胜率变化Fig.16 Change of winning rate of ablation experiment

可以看出，仅采用局部奖励回报的AC-局部算法随着训练次数的增加，对抗胜率持续上升，然而相比于本文算法，对抗胜率上升缓慢；仅采用全局奖励回报的AC-全局算法训练时，对抗胜率变化上下浮动较大，在101～200场和301～400场的训练中对抗胜率发生了大幅度的下降，缺乏一定的稳定性。由此可见，本文算法在稳定性和有效性上均优于单一采用全局奖励回报或局部奖励回报的算法，验证了本文双层奖励回报的必要性。

4 结束语

多无人机协同空战中存在许多不确定性、实时性等特点，给目标重分配问题带来了许多新的变化，基于强化学习的思想，设计了基于Actor-Critic算法的多无人机协同空战目标重分配框架，并结合空战场景的需求构建了Actor网络和Critic网络模型，设计了解决空战稀疏奖励问题的双层回报函数。实验结果表明，本文求解方法的有效性。在后续工作中，一方面将进一步考虑空战中的分布式作战特点，基于多智能体强化学习对多无人机协同空战目标重分配问题进行了研究；另一方面，目标重分配属于空战重决策问题之一，在未来的工作中可以尝试对战术决策、角色分配等环节进行重决策。