基于POMDP的多机无源传感器协同任务规划
2022-06-29彭冬亮任金磊
马 玲,左 燕*,彭冬亮,任金磊
(1.杭州电子科技大学 自动化学院,浙江 杭州 310018;2.中国运载火箭技术研究院,北京 100076)
0 引言
随着隐身飞机、反辐射导弹和电子对抗技术的飞速发展,无源探测系统不主动发射电磁信号,具有隐蔽性好、覆盖范围广等优点,被广泛应用于目标定位、跟踪、监视、导航和无线通信等领域。
在无源探测系统中,到达时差(Time of Arrival,TOA)是基本的观测信息之一[1],基于无源时差的定位跟踪算法相继提出[2-4]。TOA协同定位性能不仅与传感器量测精度有关,还很大程度上受到目标和传感器之间的几何位置影响[5]。当无源传感器部署在多个无人机上,通过优化无人机飞行轨迹可有效提高多机协同跟踪精度[6]。面向跟踪目标任务的多机无源传感器任务规划问题成为研究热点。
多机无源传感器协同跟踪根据一定的最优准则,优化无人机的运行参数使得目标跟踪系统整体跟踪性能达到最优[7]。不同优化性能指标下的无人机调度方法被相继提出[8],基于信息驱动的调度通常以信息增量[9-12]为优化指标使得多无人机协同跟踪下所获取的目标信息增益最大化。基于跟踪任务的调度通常以目标跟踪状态估计误差性能下界[13-14]为优化指标。上述调度方法仅考虑以当前调度决策产生的目标跟踪收益或代价为调度目标,而未考虑当前调度决策带来的长期跟踪性能影响,具有短视性。
多无人机远期调度将无人机飞行规划决策视为部分可观察马尔可夫决策过程(Partially Observable Markov Decision Process,POMDP),其本质属于高维非线性优化问题[7]。由于目标运动状态不确定和传感器量测不确定,加上无人机飞行约束,使得无人机远期调度策略的求解非常复杂。文献[15]将调度过程抽象为决策树问题,采用改进分支定界算法进行求解。文献[16]提出自适应多种群协同差分进化算法。上述方法具有较高的计算复杂度,无法满足任务决策的实时性需求。
对此,本文针对多无人机无源协同定位跟踪下传感器调度问题,提出了远期调度策略,并提出了一种分布式自主决策优化算法,最后仿真实验结果表明了所提传感器调度方法的有效性。
1 POMDP问题描述
NS架无人机上分别装载一部TOA无源传感器,通过优化多个无人机的运动方向协同跟踪目标。将机载无源传感器看作是一个智能体,面向目标跟踪任务的多无人机无源传感器调度可描述为POMDP,模型要素用六元组表示〈S,φ,Z,f,h,R〉。
1.1 系统状态S和状态转移函数f(·)
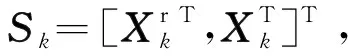
目标的状态转移方程可描述为:
Xk+1=FkXk+wk,
(1)
式中,Fk为目标状态转移矩阵,不同的目标运动模式(如匀速运动、匀加速运动等)对应不同的目标状态转移矩阵;wk为k时刻过程噪声,均值为0,方差为Q。
传感器i位置转移方程可描述为:
(2)
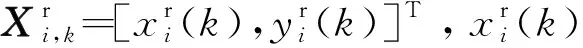
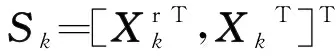
(3)
式中,f(·)为系统状态转移函数。
1.2 决策变量φ和决策空间
定义k时刻系统的决策变量φk为无人机的飞行方向,φk=[φ1(k),φ2(k),…,φNs(k)]T,其中φi(k)为k时刻无人机i的飞行方向。由于机载平台运动能力受到限制,无人机i运动方向需满足转弯率要求[5]:
Φi={φi(k)|φi,min≤φi(k)≤φi,max},
(4)
式中,φi,min和φi,max分别为无人机i飞行方向可改变的最小值和最大值。
将各无人机飞行方向在各自角度范围内等分,则无人机i的可行飞行方向满足:
(5)
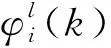
每一时刻k,无人机i的调度决策空间为
多机无源传感器协同跟踪下传感器调度决策空间为U=U1×U2×…×UNS。
1.3 观测值集Z和观测函数h(·)
定义k时刻观测值集Zk为所有无源传感器的观测值组成的集合Zk=[Z1(k),Z2(k),…,ZNS(k)]Τ。由于各个传感器独立观测,k时刻机载无源传感器i对目标的观测函数为:
Zi(k)=hi(Sk)+vi(k),
(6)
式中,hi(Sk)为传感器i的TOA观测函数,具体为:
(7)
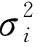
(8)
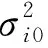
1.4 收益函数R(·)
考虑TOA量测噪声与距离相关的特点,本文采用GCRLB的迹最小化为优化指标进行传感器调度决策。高斯噪声下Fisher信息矩阵(Fisher Information Matrix,FIM)满足以下递推形式[6]:
(9)
(10)
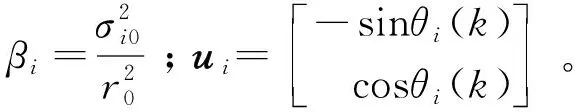
将式(8)带入式(7),有:
Jk(Sk,φk)=(Qk-1+Fk-1Jk-1-1Fk-1T)-1+
(11)
GCRLB定义为FIM的逆,以GCRLB的迹为目标跟踪代价函数,有:
R(Sk,φk)=tr(Jk(Sk,φk)-1)。
(12)
1.5 基于变增益无迹卡尔曼滤波的状态更新
在POMDP框架下,系统的状态不完全可观。为实现目标的持续稳定跟踪,在获得量测值之后需要对系统的状态进行持续更新。考虑AOA量测噪声方差随目标-传感器距离变化特点,设计一种变增益无迹卡尔曼滤波(Variable-Gain Unscented Kalman Filter,VUKF)算法对系统状态后验估计。
(13)
(14)
式中,N为Sigma点的维数;λ为标度参数,它确定围绕状态向量Xk均值的Sigma点的分布。
② 预测。计算Sigma点的一步预测及相应量测预测值:
(15)
(16)
(17)
③ 计算增益。根据目标一步预测值更新量测噪声方差,以此更新滤波器增益:
(18)
(19)
(20)
④ 状态更新。根据新的量测更新目标状态和状态协方差:
(21)
(22)
1.6 基于POMDP的多机任务规划问题
基于POMDP的多机载被动传感器协同跟踪任务规划的最终目的是在有限任务时域内,优化无人机平台的飞行方向,提高目标的跟踪性能。
令调度序列Φ1:N=[φ1,φ2,…,φN],在任务周期[1,N]内总目标跟踪代价函数为:
(23)
POMDP任务规划决策模型为:
s.t.φi(k)∈Ui,i=1,2,…,NS;k=1,2,…,N。
(24)
基于POMDP的多机无源传感器协同任务规划过程如图1所示。
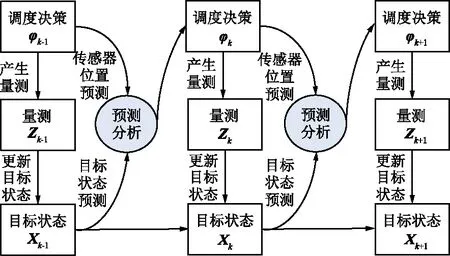
图1 基于POMDP的协同任务规划过程Fig.1 Mission planning process based on POMDP
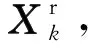
2 任务规划模型求解
2.1 基于单步决策的传感器远期调度子问题
将任务周期[1,N]内传感器调度问题分解为N个单步决策子问题,每一时刻k(k=1,2,…,N)优化决策各无人机的飞行方向φk。由于目标状态具有无后效性,k时刻的最优决策φk与过去状态无关,仅取决于当前状态Sk。k时刻,当前调度决策φk产生的目标跟踪代价为:
V(Sk)=tr(Jk(Sk,φk)-1)+V(Sk+1),
(25)
式中,V(Sk)为从当前状态Sk开始产生的目标跟踪代价,第1项为当前调度决策φk产生的瞬时跟踪性能,第2项为当前调度决策对未来跟踪性能的影响。
本文采用滚动策略迭代算法,在k时刻进行单步调度决策优化,未来[k+1,N]时段采用基本策略H对值函数V(Sk+1)进行近似。文献[18]指出,滚动策略迭代算法下调度性能具有策略改进特性,即滚动策略迭代算法性能优于基本策略H。
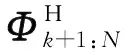
(26)
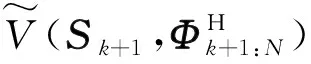
k时刻,基于单步决策的传感器远期调度子问题可描述为:
s.t.φi(k)∈Ui,i=1,2,…,NS。
(27)
2.2 传感器远期调度分布式优化求解
基于单步决策的传感器远期调度子问题决策空间为U=U1×U2×…×UNS,集中式优化求解方法将求解过程描述为决策树,每一节点数为可行调度决策,基于改进分支定界算法[17]对其优化求解,其计算复杂度为O(|U1|×|U2|×…×|UNS|),在上述离散化决策空间描述下,其计算复杂度为O((L+1)NS)。随着传感器个数NS的增加,决策树的分支呈指数增长。为了降低算法的计算复杂度,提高调度决策的实时性,本文提出了一种分布式求解算法。多传感器远期调度分布式优化决策过程如图2所示。
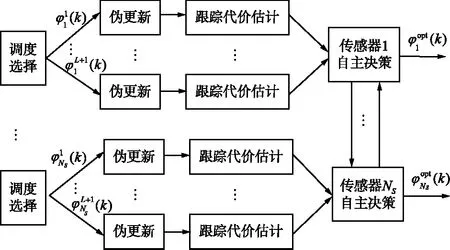
图2 多传感器远期调度分布式优化决策过程Fig.2 Distributed optimization of non-myopic sensor scheduling
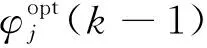
Vi(S(k),φi(k))=tr(Jk(S(k),φi(k))-1)+
(28)
式中,目标函数包括3项:第1项为传感器i调度决策产生的瞬时跟踪代价,第2项为传感器i调度决策产生的长期跟踪代价,第3项为其他传感器j调度决策对目标跟踪产生的影响。
传感器i最优调度决策为:
(29)
每个传感器在调度时刻独立进行控制决策,采用改进分支定界树算法对式(21)进行求解,其最优决策在最小化目标长期跟踪代价的准则获得,整个分布式多传感器远期调度的计算复杂度为O(NS(L+1))。与集中式调度决策相比,分布式调度决策可以极大地降低计算复杂度,提高计算效率。
3 仿真实验
仿真场景和参数设置如下:探测区域内有一个运动目标,目标初始状态[0,50,0,50]Τ,飞行时间为150 s,目标在15~25 s做左转弯运动(转弯速率为0.02 rad/s),40~50 s做右转弯运动(转弯速率为-0.02 rad/s),其余仿真时间目标做匀速直线运动。机载平台的初始状态参数如表1所示。

表1 传感器初始状态信息Tab.1 Sensor initial state information
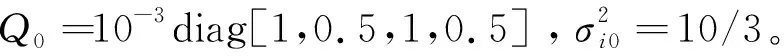
将本文算法与启发式调度[6]、短期调度[14]进行比较。不同算法下目标位置估计总误差如图3所示。

图3 不同算法下目标位置估计总误差Fig.3 Total error of target position estimation with different algorithms
由图3可以看出,本文提出的基于单步决策的远期调度算法性能最好,短期调度算法[14]次之,启发式算法[6]性能最差。随着预测步长增加,基于单步决策的远期调度算法下目标位置估计误差逐渐减小。
分别取传感器个数为2,3,5,10(对应表中前2,3,5,10个传感器),其他仿真参数不变,采用传感器远期调度算法(预测步长为4)进行仿真测试,不同传感器个数下远期调度目标位置估计平均误差如图4所示。
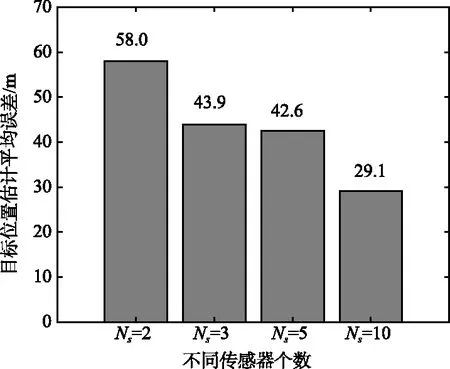
图4 不同传感器个数下目标位置估计平均误差Fig.4 Average error of target position estimation with different number of sensors
由图4可以看出,随着传感器个数的增加,目标跟踪误差减小。对多机载无源传感器组网协同跟踪,增加无人机的个数有望显著提升目标跟踪精度。
将分布式优化决策与集中式优化决策[15]进行对比仿真。仿真场景选取5个传感器(如表1所示),其他仿真参数不变。远期调度集中式决策和分布式决策求解算法下目标跟踪性能和计算性能对比分别如图5和图6所示。
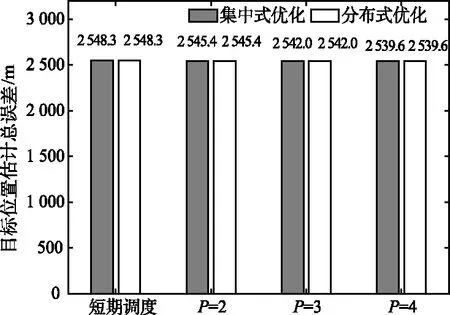
图5 集中式和分布式算法性能对比Fig.5 Performance comparison of centralized and distributed algorithms
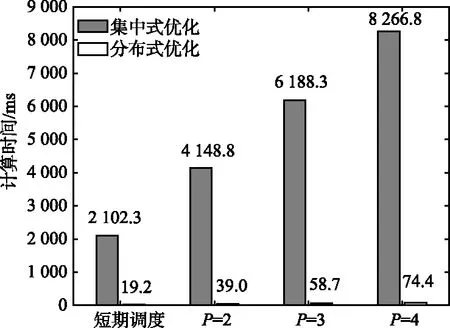
图6 集中式和分布式求解算法计算性能对比Fig.6 Computational efficiency comparison of centralized and distributed algorithms
由图5和图6可以看出,分布式优化求解算法下目标跟踪精度与集中式优化求解算法的跟踪性能非常接近,但分布式优化求解算法的计算效率显著提高。随着预测步长的增加,集中式优化求解算法的计算复杂度呈指数增长,无法满足实时性要求。而分布式优化算法能够在保证一定跟踪性能的前提下,大大降低算法复杂度,能够很好地满足在线调度的实时性需求。随着多传感器个数的增加,分布式优化求解的优势将更明显。
4 结束语
针对多机载无源传感器协同跟踪问题,提出了一种基于长期跟踪代价的多无人机无源传感器调度算法。首先,在POMDP框架下建立了基于GCRLB指标的传感器远期调度模型。随后,采用滚动时域方法将多阶段问题分解为多个单步决策的调度子问题,考虑当前决策对未来长期跟踪性能的影响。然后,设计了一种基于分布式自主优化求解算法,通过对多个传感器独立自主决策,在保证目标估计精度的基础上提高传感器调度的灵活性和快速性。最后,理论分析和仿真测试验证了算法的有效性。
