无人机与物流柜协同配送最短路径问题启发式算法
2022-06-29朱外明梁培培刘根节赵亚娟
朱外明,梁培培,刘根节,赵亚娟
(安庆师范大学 经济与管理学院,安徽 安庆 246133)
0 引言
随着5G通信等相关技术的快速发展,无人机被越来越多地应用到物流领域[1]。使用无人机配送包裹具有快速、安全、24 h可用、环境友好、不占用道路交通资源和解放人力等优势。目前,谷歌、UPS、DHL、亚马逊、京东、顺丰和中国邮政等国内外一些物流企业在物流无人机领域持续多年投入研究,并积累了大量的无人机配送实践经验。在该领域,一种使用无人机与物流柜协同配送包裹的方式具有较高的实用价值和广阔的应用前景。目前,已有若干企业成功地将该模式应用到城市的快餐、血浆和核酸样本等运输场景中,取得了一定的成效。
在该模式中,物流柜的柜顶部设有自动化装卸包裹的装置,并作为无人机的起降平台,无人机在物流柜顶部自动完成包裹的装载,飞行到指定的物流柜顶部后自动完成包裹的卸载。由于该过程需要较少的人力干预,因此自动化程度较高,适用于“非接触”式的配送场景。由于一个物流柜的顶部一次只能供一架无人机停靠,即无人机对物流柜具有独占性,因此固定数量的物流柜成为多架无人机“竞争的稀缺资源”,这也导致在该模式下,无人机的任务规划问题具有一定的难度。
无人机携带货物从发出地飞往接收地,其有序访问的多个物流柜之间的路线连起来构成路径[2-3],可行的规划方案包含每架无人机的飞行路径。无人机需要在物流柜上装卸货物和更换电池,且无人机对物流柜具有独占性[4-5],即一个物流柜一次只能服务一架无人机,可行的规划方案包含无人机在物流柜上的停靠方案。由于无人机飞行需要消耗电能,如何制定出综合的路径与停靠方案,让无人机完成全部任务的配送,使得飞行的总路径最短?这就是本文研究的无人机与物流柜协同配送最短路径规划问题(Drone and Locker Cooperative Delivery Problem with Total Distance Minimization,DLDP-TDM)。
由于DLDP-TDM是一个路径规划与机器调度深度耦合的问题,其建模与求解具有一定的难度。与该问题相关的经典运筹问题包括车辆路径[6-7]、机器调度[4-5]、无人机任务规划[8-9]和岸桥调度[10]等,而这些都只与DLDP-TDM的部分特征相似。生产运输规划问题[11-12]与DLDP-TDM的相关程度较高,但是二者也存在本质的区别,即生产运输规划是机器调度与路径规划的集成问题,而DLDP-TDM是二者的耦合问题。此外,近年来,基于车机协同[13-14]的规划问题也成为热点,主要包括带无人机的旅行商问题(Traveling Salesman Problem with Drone,TSP-D)[15-19]和带无人机的车辆路径问题(Vehicle Routing Problem with Drones,VRP-D)[20-21],例如,经典的“Horsefly Routing”[14]“Flying Sidekick”[15]等。在这些问题中,无人机与载机平台(例如卡车)[22]是一一对应的,无人机不在载机平台间切换飞行,因此与DLDP-TDM问题并不相同。目前,未发现国内外有关于DLDP-TDM问题的研究工作。
本文深入分析了DLDP-TDM问题的特征,找到了最优解的一个下界,定义了任务子集可执行的条件,介绍了任务环在执行前后系统状态保存不变的性质,设计了求解规划问题高效的启发式算法。选取了中国9座城市,从中选取著名的商业中心等地,使用真实企业的无人机数据,进行了仿真验证。模拟3种不同的无人机配送场景,生成了3组共81个仿真算例,计算结果表明,提出的启发式算法具有优效性。
1 问题描述与数学模型
设指定区域内有物流柜与无人机协同配送系统,系统的硬件由分布在m个指定站点的物流柜和停靠在物流柜上的无人机组成,第i个站点处设有bi个物流柜,bi也可记作b(i),每个物流柜k∈K顶部最多只能停靠一架无人机,无人机的总数不超过物流柜的总数|K|,使用D表示无人机的集合。无人机d∈D可以在物流柜上自动装载包裹,飞行至另一物流柜的顶部,并完成包裹的自动卸载。无人机每次最多只能携带一个包裹。无人机每次飞行完成后,需要在物流柜的顶部更换电池,假设这一过程也是自动化的。
对于给定的协同配送系统,配送任务(以下简称任务)集J由多个待配送的包裹组成,配送任务j∈J对应一个源站点rj和目的站点kj,站点rj到kj的距离记为dj,每个包裹均需要由无人机进行配送。包裹在源站点的物流柜是固定的,可以运输到目的站点的任一物流柜。无人机的飞行需要消耗电能,且所消耗的电能与无人机飞行的距离是相关的,本文假设无人机飞行时载货与否不影响能量的消耗,且无人机的能量消耗与飞行距离成正比例关系。因此希望无人机能够使用最短的飞行距离完成全部的配送任务。
虽然时间也是任务规划的经典优化目标之一,但是却不在本文的考虑范围之内。一方面,因为在本文考虑的配送场景中,能量消耗所形成的成本远远高于因时间延误所形成的成本;另一方面,因为无人机飞行速度较快,且均沿直线飞行,大部分配送包裹均能在指定的时间内运输到目的地。
1.1 优化目标
无人机完成全部配送任务的总距离是规划问题的优化目标,该目标函数由哪几部分组成呢?因为无人机一次最多只能携带一个包裹,所以无人机的飞行主要包含2种类型:空载飞行和载物飞行。由于所有的包裹均需配送,因此每个包裹从源站点到目的站点之间的飞行距离必须全部计入目标函数。因此,可以轻松得到规划问题最优解的下界,即性质1。

另一方面,由于无人机必须停靠在物流柜上,给定数量的物流柜成为无人机竞争的资源,因此必须添加一定数量的空载飞行才能确保规划方案的可行性。定义无人机的空载飞行为辅助任务。任意2个站点之间均可能形成辅助任务,设e=i→i′为从站点i到i′的飞行航线,E={e|∀i≠i′,i≤m,i′≤m}为任意2个站点间飞行航线的集合,de为航线e的距离,xe∈Z+∪{0}为需要添加的飞行航线e的次数,则优化目标为:
(1)
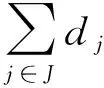
(2)
将每架无人机飞行经过的物流柜连起来,能够构成一条连贯的路径,因此总体规划包含路径规划子问题。在路径规划问题中,经典的数学模型是基于路径的集合分区模型。使用u表示无人机的一条路径,无人机d的所有可行的路径集合记为Ud,全部无人机路径的集合为U={Ud|d∈D}。给定路径u,其包含的辅助任务是固定的,使用参数pe,u∈Z+∪{0}表示在路径u的辅助任务中航线e的飞行次数。使用0~1决策变量xu表示是否选择路径u,式(2)可写为:
(3)
1.2 约束条件
从无人机的视角来看,由于每个无人机只能从各自的路径集合中选择一条路径作为执行方案,因此建立式(4):
(4)
给定路径u,其是否执行了任务j是已知的,使用参数gj,u∈{0,1}表示任务j是否在路径u中得到执行。由于每个任务只需要执行一次,因此建立式(5):
(5)
从物流柜的视角来看,每个物流柜一次仅供一架无人机停靠,类比于机器上一次只加工一个工件,无人机在物流柜上的停靠行为类比于待加工的工件,因此总体规划包含机器调度子问题。给定路径u,其飞行经过的物流柜是已知的,使用fk,u∈Z+∪{0}表示路径u在物流柜k上的停靠次数,则物流柜k上的停靠行为总数可用决策变量表示为:
vk=∑u∈Uxu·fk,u。
(6)
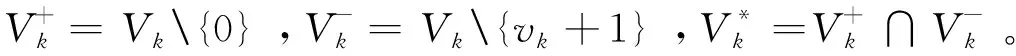
(7)
(8)
(9)
(10)
(11)
式(7)表示从虚拟的停靠行为0开始,式(8)表示到最终的停靠行为vk+1结束,式(9)表示每个实际的停靠仅有一个紧前和紧后停靠行为,式(10)表示每个实际的停靠行为必须被选中一次,式(11)表示物流柜上一次只能服务一个停靠行为。
式(3)~式(5)和式(7)~式(11)为DLDP-TDM的数学模型。由于vk是依赖于决策变量xu的,因此,式(7)~式(11)也依赖于决策变量xu。上述模型是一个两阶段优化模型,求取问题的精确解具有一定的难度。本文深入分析规划方案内部的结构特征,提出了一种构造启发式算法,能够求得问题高质量的可行解。
2 启发式算法
定义协同配送系统状态为各站点上无人机的停靠数量,记为s,它会随着无人机位置的变化而变化,即每次无人机完成一次飞行后,系统状态可能会发生改变。使用f(i,s)表示在状态s下站点i上停靠的无人机数量。在给定系统状态下,有些任务可以直接执行而不需要添加辅助任务。对于任务j,如果当前系统状态满足:
f(rj,s)>0,
(12)
f(kj,s) (13) 则j为在当前系统状态下可执行任务,使用T(s)表示在状态s下所有可执行任务的集合。 需要特别说明的是,在判断j是否可直接执行时,只需检查其源站点是否有无人机停靠即可,而无需检查存放包裹的物流柜上是否停靠有无人机。这是因为即使存放包裹的物流柜上没有停靠无人机,但同站点其他物流柜上有无人机时,也可以使用其他物流柜上的无人机执行运输任务。无人机在同站点的物流柜之间切换飞行时消耗的能量可以忽略不计。 由若干任务首尾相连可以形成任务环,如果任务环中有至少一个站点停靠有无人机,则整个任务环可以直接执行而不需要添加辅助任务。可以从2个特例说明:① 如果任务环中只有一个站点停靠有唯一的无人机,则可以由该无人机依次运输包裹,直至完成全部任务,并返回初始站点;② 如果任务环中每个站点的每个物流柜上均停靠有无人机,则每个站点可以同时起飞一架无人机运输包裹,即实时运输。使用C表示任务环,I(C)为环C中的站点集合,则基于上述2个特例可以分析得到,如果任务环C满足: (14) 则环C为系统状态s下的可执行环。 而且当环中的任务被执行完以后,环中每个站点停靠无人机的数量与执行之前是相等的。因为在执行任务后,环中每个站点飞入无人机的次数与飞出无人机的次数相等。因此,执行任务环的前后除了任务数减少以外,系统状态不发生改变,即性质2。这为设计启发式算法提供了思路。 性质2:设C(s)为系统状态s下的可执行环,s′为执行C(s)全部任务后的系统状态,则有:s′=s。 优化目标为最小化无人机飞行的总距离,因此,应当尽可能少地使用辅助任务。由于执行任务环前后系统状态不变,而使得待执行任务减少,因此,应当尽可能多地先执行环。而当系统中找不到可执行环时,应当尽可能地安排可执行任务。而一旦某个任务被执行后,系统状态又发生改变,此时可以再次尝试搜索可执行环。重复上述操作,直到找不到可执行任务时停止。 当存在未安排的任务且基于当前系统状态无法搜索到可执行任务时,需要通过添加辅助任务调动无人机以改变系统状态,使得某个任务得以执行。而一旦该操作执行以后,系统的状态又会发生改变,因此又可以搜索可执行环或可执行任务。按照该思路设计启发式算法,能够使得全部任务得以规划,具体算法如下。 算 法:启发式算法输 入:系统状态s,待配送任务集J,空规划方案Q输 出:更新的规划方案Q步骤1:如果J≠∅,转步骤2,否则转步骤8;步骤2:如果存在环C满足式(14),转步骤3,否则转步骤4;步骤3:执行环C,令Q=Q∪C ,令J=JC,转步骤1;步骤4:如果存在T(S)⊆J使得∀j∈T(S)为可执行任务,转步骤5,否则转步骤6;步骤5:选择j∈T(S)执行,令Q=Q,j ,令J=Jj,更新系统状态s,转步骤1;步骤6:如果存在l∈J,使得添加辅助任务集合O后l可执行,转步骤7,否则转步骤1;步骤7:添加辅助任务集合O,执行O和l,令Q=Q∪O,j ,令J=Jj,转步骤1;步骤8:J=∅,算法执行结束,输出Q。 算法中,判断系统中是否存在任务环可使用树搜索的方法。具体而言,从系统的某个站点开始,沿着以该站点作为源站点的任务搜索到下一个站点,不断重复上述搜索,如果某一站点在此过程中被遍历2次,则一定存在任务环。使用该方法不仅可以判断任务环的存在,还能够找出对应的任务环。需要说明的是,每次仅需要搜索到一个任务环即可,而无需一次性地搜索出全部的任务环。这是因为搜索出的任务环如果是可行的且被执行后会从任务集合中删除,因此可以使得后续的搜索规模不断地减小。 添加辅助任务总体可以分为3种情况:① 源站点没有无人机,目的站点有空闲的物流柜,需要从其他站点调来无人机执行任务;② 源站点有无人机,目的站点没有空闲的物流柜,需要调走目的站点的无人机以创造空闲的物流柜;③ 源站点没有无人机,目的站点也没有空闲物流柜,既需要调来无人机执行任务又需要创造出空闲的物流柜。为使总目标尽可能地小,应当尽量地使所添加的辅助任务的距离尽可能的短。因此,为每个需要添加辅助任务的实际任务寻找最短的辅助任务,然后从全部待添加的实际任务中选择一个辅助任务距离最短的进行执行。 为验证启发式算法的优效性,进行了仿真计算实验。选取我国9座城市,并从9座城市中选择了著名的小区、医院和餐馆/商业中心等,基于第三方地图软件开放平台获取经纬度和直线距离数据。每个站点物流柜的数量在[1,4]之间随机生成。设置数量分别为20,50,80共3种不同的任务规模,每个城市、每个任务规模下随机生成任务数据,共生成27个算例(S01~S27)。使用某一线企业真实投入使用的无人机数据,航速和最大续航里程分别为60 km/h和25 km。使用Java编程实现算法程序,基于CPU为i5-8265、内存为8 GB、操作系统为Windows10 Home Basic的计算机完成仿真计算。求解的统计结果如表1所示。 从表1中可以看到,在每个算例中,站点个数比较均匀地分布在25~40之间,而无人机的数量少于等于对应的站点数量。无人机飞行的总距离即为目标函数值,它是配送任务总距离与辅助任务总距离之和。其中,辅助任务距离占比等于辅助任务总距离与配送任务总距离的比值。根据性质1可知,后者为最优目标函数值的下界,定义辅助任务距离占比为: (15) 从表1中可以看出,最小值为6%,最大值为24%。从最后一列可以看出,启发式算法求解全部算例的计算机运行时间均在1 s以内,说明了所设计的启发式算法高效。 表1 基于均匀分布随机生成仿真算例计算求解统计结果Tab.1 Statistical results for solving the simulated instances generated following a uniform distribution 上述算例集(记为SET-1)中,配送任务是均匀随机生成的。在某些应用场景中,配送任务的数据具有一些新的特征,因此在上述选取站点数据的基础上,模拟了另外2种场景,生成了另外2组新的配送任务数据集。第2个数据集(SET-2)模拟餐馆送餐场景,配送任务由少量的餐馆运送至数量较多的小区;第3个数据集模拟血清或核酸样本送检场景,配送任务由数量较多的小区运输至数量较少的医院。求解后,记录算法求解每个算例的计算运行时间,结果显示,所有算例均能在1 s以内求得可行解。另外,记录每个算例解的辅助任务距离占比,并按照任务数量分组,绘制出统计图,如图1所示。 (a) 任务数20时各城市对应3种场景的辅助任务距离占比 (b) 任务数50时各城市对应3种场景的辅助任务距离占比 (c) 任务数80时各城市对应3种场景的辅助任务距离占比图1 不同任务规模对应3种配送场景求解结果的辅助任务距离占比曲线Fig.1 The plot of the distance ratios between auxiliary and delivery tasks for three distribution scenarios with different task scales 从图1可以看到,所有算例的辅助任务距离占比均介于[0,1],说明所添加的辅助任务的总距离均小于配送任务的总距离。在3种任务规模下,数据集SET-1对应的曲线明显低于SET-2和SET-3,这说明对于第2和第3个数据集模拟的配送场景,需要添加更多(更长)的辅助任务。这一点不难分析,因为后2个场景中,配送任务的运输方向不是“平衡”的,需要更多的调动无人机改变系统状态,以使得后续的配送任务得以执行。SET-2和SET-3对应的曲线高度比较接近,这说明,这2种配送场景虽然不同却具有某些相似的特征。另外,随着任务数的增加,SET-1对应的曲线与SET-2,SET-3的曲线之间的距离呈现增大的趋势,这是因为SET-1的配送任务始终较为“平衡”,而SET-2和SET-3的配送任务的不“平衡”特征随着任务数的增加而益发明显。 本文研究了使用无人机与物流柜协同执行物流配送任务的最短路径问题,即制定无人机的飞行计划,使得无人机以最短的总飞行距离完成全部的配送任务。该问题是一个路径规划与机器调度深度耦合的复杂优化问题。本文深入地分析了问题特征,找到了评估解质量的下界;发现了任务环这一特殊的任务结构,以及机柜系统执行任务环的前后系统状态不变的性质。基于这些发现,设计了高效的启发式求解算法。基于真实的城市地理位置、距离数据和无人机数据,进行了仿真实验。模拟了实时配送、快餐配送和样本送检3种不同的配送场景,生成了对应的数据集。求解结果表明,所设计的算法均能在短时间内求得问题高质量的解。 DLDP-TDM的优化目标为最小化无人机飞行的总距离,该问题没有考虑时间效率的影响。今后将研究DLDP-TDM的扩展问题。例如,在部分场景中,任务具有严格的时间窗口限制,即必须在指定的时间内执行任务,带时间窗约束的规划问题更难求解。此外,在飞行总距离相同的情况下,不同的任务执行顺序对应不同的完成时间,如何制定规划使得无人机在尽可能短的时间内完成全部配送任务,对于提高协同配送系统的利用率具有一定的意义。

3 仿真实验



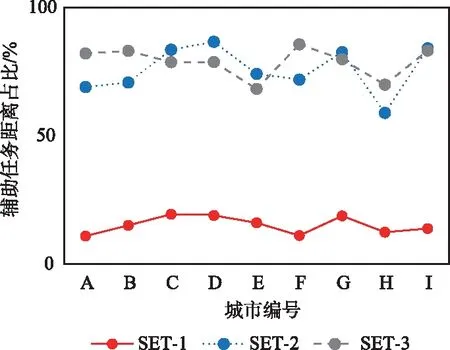
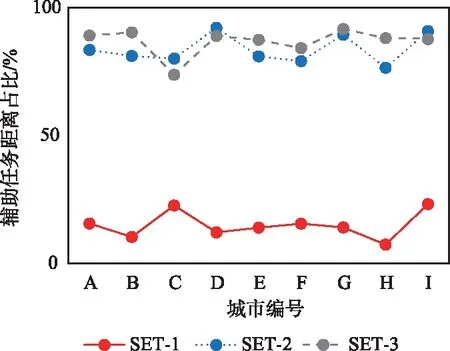
4 结束语
