星地协同架构下的高精度自主轨道预报方法
2022-06-29常中祥周忠宝邢立宁
常中祥,周忠宝,姚 锋,邢立宁
(1.湖南大学 工商管理学院,湖南 长沙 410082;2.国防科技大学 系统工程学院,湖南 长沙 410073;3.西安电子科技大学 电子工程学院,陕西 西安 710075;4.应急管理智能决策技术湖南省重点实验室,湖南 长沙 410082)
0 引言
卫星轨道预测是在卫星当前状态下,通过卫星运动学方程或数学分析来预测卫星的位置和速度,在卫星导航、卫星测控和卫星任务规划等方面发挥着重要作用。随着卫星平台的发展,卫星具有自主性和智能性,从一个简单的执行机器演化为一个自决策代理。为了自主决定星上任务,卫星必须具备基于卫星子系统实时状态、环境条件和任务分布的自主任务规划能力。因此,一种空间小、计算速度快、精度高的星载轨道预测方法是自主任务规划的前提。
现存卫星轨道预报方法可以分为3类。第1类卫星轨道预报方法采用分析方法[1-2],基于卫星在某一时刻的平均轨道根数,给出未来一段时间内的卫星轨道数据。第2类基于多项式拟合方法[3-4],在不考虑卫星受力的情况下,利用多项式拟合卫星的精确轨道,得到卫星的速度场,并给出未来一段时间内的卫星轨道数据。第3类基于动态轨道拟合方法[5-6],在已知卫星位置坐标的基础上,采用动力学方法计算初始轨道和动力学参数,然后通过积分得到轨道外推方程。前2种卫星轨道预报方法,预报的轨道参数精度随着预报时长的增加,呈现明显的下降趋势,无法实现长周期的高精度轨道预报,而第3种依赖于高精度动力学模型,随着轨道预报精度要求的提高,存储资源、计算资源的消耗不断增加,而且该方法随着卫星轨道预报周期的增加,同样难以维持高精度的轨道预报。
本文以星上自主任务规划新需求为牵引,充分考虑卫星星载计算平台的计算、存储能力现状,将基于星地协同架构,设计一种快速、准确的长周期星上高精度自主轨道预报(High Precision Autonomous Orbit Prediction Based on Satellite-ground Cooperative Architecture,HPAOPS&G)方法;阐述了卫星轨道预测方法相关研究现状,分析了星上轨道预测的难点;介绍了HPAOPS&G的原理;提出了一些实验,并给出了一些结论。
1 研究现状分析
如何提高卫星轨道预测精度是现存众多卫星轨道预报学术研究的主要关注点。Li等人[7]提出了一种基于轨道根的卫星轨道预测算法,可以有效提高卫星轨道预报的预测精度。Doornbos等人[8]通过添加2行数据对热层中性密度模型进行了校准,提高了轨道预测的准确性,但并未提及算法的计算速度和模型的复杂度。Diao等人[9]使用SGP4模型针对TERRA卫星进行卫星轨道预报,其卫星轨道预测精度较高。Wang等人[10]根据GPS伪距观测数据,采用简化的动态最小二乘批处理方法,通过引入经验加速度来确定地球的低轨卫星,并与之后的精确轨道数据进行比较,其方法较好地提高了卫星定轨精度。Feng等人[11]建立了卫星轨道预测模型,考虑了重力、大气阻力、月球重力和非球形地球引起的太阳重力等扰动。然后,用STK工具箱中的J2,J4和HPOP进行了对比实验,结果表明,该模型的预测结果存在一定误差,但满足卫星轨道预测的精度要求。Wang等人[12]采用简化的动态拟合方法进行预测,分析了不同拟合区间对预测精度的影响,并对CNES的精密星历进行了误差分析。Abay等人[13]提出了一种轨道预测算法,同时考虑了算法的速度和轨道预测的准确性。Zhao等人[14]利用动态定轨方法,根据卫星激光测距的6个月数据,获得精确的卫星轨道信息,并与法国多普勒正交法和卫星集成无线电定位(DORIS)系统得出的轨道进行了比较,分析了轨道预测的精度。Tang等人[15]使用平均大气模型对天宫一号的长期轨道进行了预测,并进行了几次为期20 d的预测试验,其中大多数试验显示半长轴误差优于700 m,总体位置误差优于400 km。Gao等人[16]对比分析了切比雪夫曲线和最小二乘曲线拟合HY-2卫星精密轨道的精度,结果表明,最小二乘曲线拟合效果更好。仅有的文献综述表明,卫星轨道预报的精度得到了不同程度的提高,即依赖于地面强大计算能力的卫星轨道预报方法已经可以保证较高定轨精度的卫星轨道预报。
然而,这些研究存在统一的不足,即没有考虑到计算空间的成本和计算速度要求。事实上,卫星星载计算机和地面计算机在计算空间和计算速度上存在很大差距。因此,十分有必要设计一种存储空间小、计算速度快、定轨精度高的卫星自主轨道预测方法,用于卫星星上长周期轨道预测,兼顾高定轨精度要求和低计算压力。
2 问题建模和求解
2.1 问题描述
结合实际工程和学术研究,本文提出2种用于卫星星上长周期轨道预报的星上自主轨道预报解决方案:
① 依托地面强大的计算能力,进行长周期的卫星轨道预报,得到未来一段时间的完整卫星定轨数据,然后,通过地面测控站,在有限的卫星测控窗口内,向卫星注入长周期的所有定轨数据;
② 地面测控站只需要向卫星注入初始轨道参数(卫星瞬时轨道根数),然后依托卫星星载计算机,自主进行卫星轨道预报。
目前,卫星和地面站无法实现实时、高速的通信,尤其是在中国“国内站、一天、一测控”的条件下,星地通信是主要用于传输成像数据的宝贵资源,无法满足大数据量的遥测信息和地面控制指令等数据的传输要求。一天的轨道数据量通常可达7 MB以上,以GPS Block IIF[17]为例,地面与卫星之间的上行速度仅为200 kb/s。低轨道卫星(500 km)与地面站之间的可见时间窗口约为10 min。如果使用第1种解决方案,注入一天的轨道数据将花费大约300 s,这大约占可见窗口的一半。考虑到需要注入的其他重要信息(如紧急远程控制命令和应急观测任务等),第1种解决方案显然不是明智的解决方案。
然而,第2种解决方案存在一系列技术障碍,无法很好地应用于实际工程。精确模型(Precise Model,PA)[18]将占用数十兆字节,需要考虑50×50阶引力模型、太阳引力模型、月球引力模型、太阳辐射模型、大气阻力模型和潮汐扰动模型等。以RAD750[19]为例,其星载计算能力仅为266 MIPS,未达到后文数值仿真试验使用计算机计算能力的1/10。这意味着星载计算机无法满足精确轨道预测的计算要求。因此,单纯使用第2种解决方案依然无法很好地解决卫星自主轨道预报问题。
考虑到星地通信的现状和星上星载计算、存储能力,设计了一种快速、准确的长周期HPAOPS&G。其中,具有强大计算能力的地面采用高精度轨道预报方法(PA)预报未来一段时间内的卫星定轨参数,获得固定时间间隔的卫星轨道瞬根。然后,通过北斗等高轨道卫星将这些卫星轨道瞬根快速地注入卫星系统,卫星使用简化轨道预测算法(Simplified Orbit Prediction Algorithm,SA)进行分段轨道预报。HPAOPS&G有效降低了星上计算成本、存储空间消耗和星地通信链路的占用率。
2.2 轨道参数定义
本文采用J2000坐标系的时间、位置和速度表示卫星轨道瞬根,HPAOPS&G使用到的参数定义如表1所示。

表1 HPAOPS&G中的参数定义Tab.1 The definition of parameters in HPAOPS&G
关于上述参数,有几种计算方法:
(1)
(2)
(3)
2.3 算法原理
星地协同架构下的HPAOPS&G的原理如图1所示。

图1 HPAOPS&G算法原理Fig.1 Principle of HPAOPS&G algorithm
具体步骤为:
① 现有丰富的卫星轨道预报研究表明,在不考虑计算成本的情况下,轨道预报定轨精度可以无限接近实际值。因此,在HPAOPS&G中,地面部分将采用尽可能高精度的PA,例如考虑了50×50阶重力模型、太阳重力模型、月球重力模型、太阳辐射模型、大气阻力模型和潮汐扰动模型等。当然,后续研究可以根据实际需要改变PA。
② 根据轨道预测的精度要求,设定分段间隔时间(IT),这是本文的重点之一,然后在地面上通过PA生成分段轨道根。
③ 通过北斗等高轨道卫星,地面系统可以随时向卫星注入分段轨道根。因此,地面预测周期不需要太长。
④ 基于分段轨道根,SA预测机载轨道数据。SA不仅减少了占用的空间,而且大大提高了计算速度,本文使用的SA只考虑了二阶重力模型。后续研究也可以根据实际需要改变SA。
2.4 算法说明
为了说明SA的计算速度显著快于PA,列举了一组SA和PA轨道预报对比试验,采用相同轨道瞬根参数,如表2所示。

表2 轨道瞬根参数Tab.2 Satellite orbit instantaneous elements
PA和SA均采用C++编码,运行环境为i7-3520M (2.90 GHz) CPU、12.0 GB RAM的计算机。使用PA和SA分别预报未来10 800 s内的卫星轨道数据,并独立重复运行每个算法100次,以获得运行时间的平均值。PA(1.038 6 s)的运行时间大约是SA(0.021 s)的50倍。
然而,SA预报的定轨精度损失变化如图2所示。

(a) SA预报定轨位置精度损失
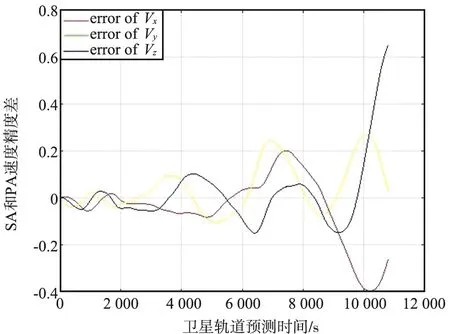
(b) SA预报定轨速度精度损失图2 SA预报定轨精度损失Fig.2 Accuracy loss of orbit prediction by SA
由图2可以看出,SA和PA之间的差异越来越大。SA的预报定轨精度随着预测时间的增加而不断下降,达到10 800 s(459.24,466.79,174.69 m;-0.26,0.025,0.65 m/s)。
对比试验结果表明:① PA的预报定轨精度较高,但计算速度较慢,需要消耗的计算资源较多;② SA的计算速度较快,但随着预测时间的增加,SA的预报定轨精度显著降低;③ 这2种算法均无法直接应用于星上自主轨道的预报。
3 数值仿真试验
对比试验结果(如图2所示)显示,6个参数的预报差值存在有正负值,为此,接下来的仿真实验将使用绝对差来测量定轨精度的损失。本节通过数值仿真实验来探索IT与预测定轨精度之间的关系,以指导实际工程应用。此外,还介绍了HPAOPS&G对计算速度的改进。
3.1 分段间隔时间与预测定轨精度之间的关系
结合HPAOPS&G的算法原理,将分段间隔时间分别设置为600,900,1 200,800,2 400,3 600 s,并基于表2所示的初始轨道瞬根参数,采用SA预报未来10 800 s的卫星轨道数据。然后应用2.2节中的式(3),得到了每个分段间隔时间下的时间段内差值绝对值的最大值,如表3所示。结果表明,SA的预报定轨精度随着分段间隔(3 600~600 s)的不断减小而显著提高。
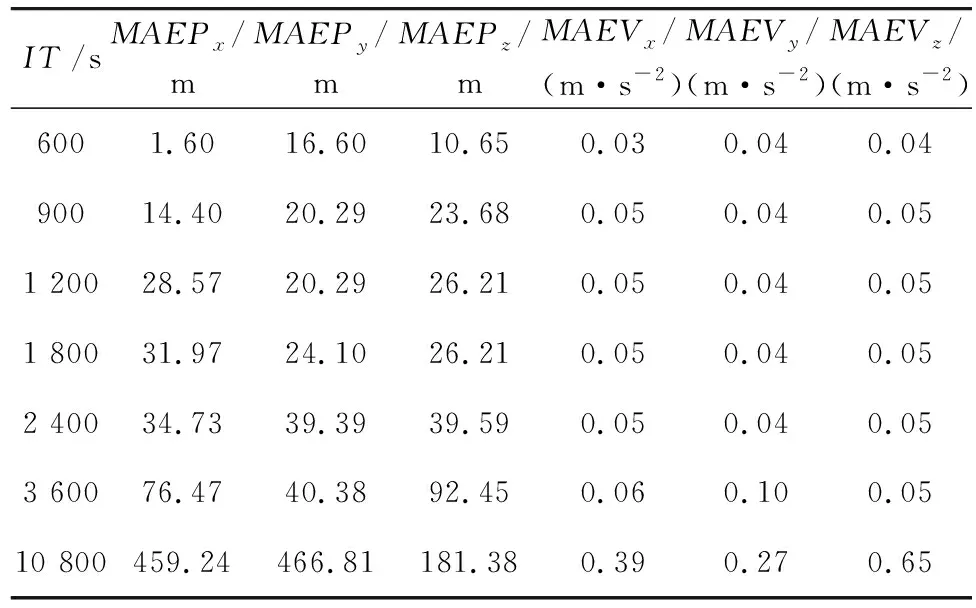
表3 SA预报定轨精度损失变化Tab.3 The variation accuracy loss of forecast orbit on the position by SA
不失一般性,以MAEPx精度损失为例,探讨IT与预报定轨精度之间的关系。用最小二乘法拟合,求出IT与MAEPx的关系式:
MAEPx=-0.000 1×IT2+0.124 9×IT-54.818 1。
(4)
拟合曲线如图3所示。基于式(4),实际工程应用中,操作员可以根据所需的预报定轨精度,科学、准确地设置HPAOPS&G轨道预报的IT。由于原理相似,不再描述其他参数与IT之间的关系。
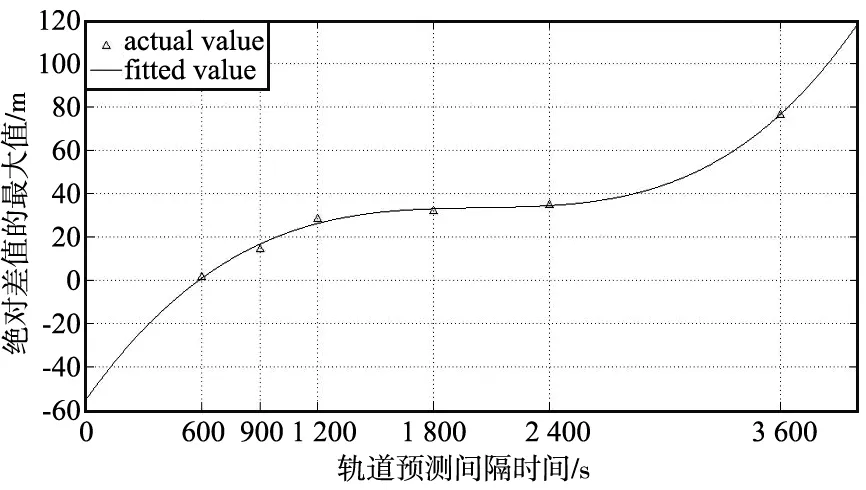
图3 最小二乘拟合曲线Fig.3 The least square fitting curve
3.2 并行计算下的HPAOPS&G
HPAOPS&G具有良好的并行计算基础,为了更加适应于实际工程应用的需求,提升其轨道预报定轨精度、减低算法运行耗时,本节采用并行计算方法,分析算法并行计算下的预报耗时。采用表1所示的初始轨道瞬根参数,基于HPAOPS&G采用并行计算和串行计算分别预报未来10 800 s的卫星轨道数据,并独立重复运行算法100次,得到如表4所示的运行时间的平均值。
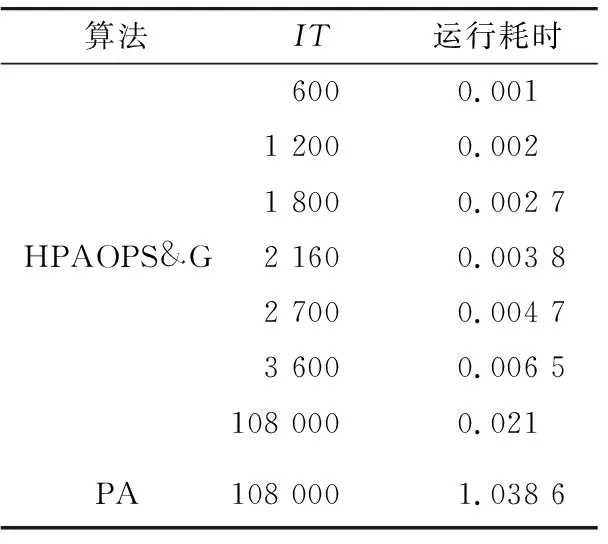
表4 轨道预报平均耗时Tab.4 Average time of orbit prediction 单位:s
使用并行计算的HPAOPS&G的轨道预报运行耗时显著减少,IT为600 s的HPAOPS&G的轨道预报运行耗时仅为无分段下HPAOPS&G的IT的1/21左右。
4 结束语
本文分析了卫星轨道的预报研究、卫星星载平台计算、存储能力现状以及星地通信能力的发展现状,提出了一种全新的卫星轨道预报方法HPAOPS&G,有效地兼顾预报定轨精度、计算耗时以及星地通信负荷,成功解决了星载计算能力较弱情况下的星上自主轨道预报问题,为星上自主任务规划、自主运行提供了技术支撑。
另外,通过最小二乘拟合,给出了分段间隔时间与预报定轨精度之间的关系式,以指导实际工程应用。而且,引入并行计算方法,有效地提高了HPAOPS&G的卫星轨道预报的计算速度。
