基于DPRI的单行为强化聚类算法

张龙，李凤莲，张雪英，史凯岳

（太原理工大学信息与计算机学院，山西榆次 030600）

K-means 算法是一种简单高效易于实现的基于划分的聚类算法，该算法的计算复杂度接近线性，但初始聚类中心的选择和样本的划分方式均会对聚类性能产生较大的影响[1]，因此，一些改进算法相继被提出。K-means++算法使用最大最小距离法选取初始聚类中心，尽可能选取相对距离较远的样本作为初始聚类中心，一定程度上减小了随机选取初始聚类中心对聚类性能的影响[2]。文献[3]将K-means 与关系对称矩阵和社会网络分析中的度中心性相结合，并对K-means 算法初始聚类中心的选择进行了优化，提高了聚类算法的性能。文献[4]提出基于特征关联度的K-means 初始聚类中心优化算法，可得到更优的聚类结果。上述改进主要是针对初始聚类中心选取开展的研究，对聚类算法样本划分方式未进行改进。

模糊聚类[5](Fuzzy C-Means，FCM)算法将样本的硬划分转化为一种柔性的模糊划分，以此更科学地度量样本相似度。文献[6]在FCM基础上，提出了一种密度加权FCM 算法，文献[7]提出了基于迭代信息熵权的改进LFCM 聚类算法。上述FCM 及其改进算法主要以样本的划分方式为切入点进行改进，提高了聚类性能，但处理中规模和大规模数据时的复杂度较高。

近年来，随着强化学习在AlphaGo上的成功应用，将强化学习和聚类算法相结合也成为一个新的研究方向。学习自动机[8]作为一种强化学习算法，使用该算法对聚类算法进行改进是近年来的一个热点。文献[9]提出了学习自动机聚类算法(Learning Automata Clustering，LAC)。受该文献启发，文中提出了一种基于DPRI(Discretized Pursuit Reward Inaction)的单行为强化聚类算法，在聚类过程中引入DPRI算法中的离散更新技术，去除了算法中智能体(Agent)行为概率之和必须为1 的约束，把行为概率转换为累积奖励，并引入ε贪婪策略，提升了Agent 选择行为的速度，有效降低了时间复杂度。

1 基础理论

1.1 强化学习

强化学习[10](Reinforcement Learning，RL)又称增强学习，通过模拟人类学习过程中的“探索”和“利用”机制，把待分析问题抽象为马尔科夫决策过程[11](Markov Decision Process，MDP)。该过程中，如果Agent 的某个行为得到系统的正向反馈，那么Agent选择该行为的趋势就会增大；如果Agent 所选行为得到系统的负向反馈，那么Agent 选择该行为的趋势就会下降。强化学习的目的就是在学习过程中使得到的奖励最大化。

1.2 马尔科夫决策过程

马尔科夫决策过程(MDP)是一个四元组＜S,A,T,R＞。其中，S={s1,s2,…,sn}表示包含该过程中所有状态的有限集合；A={a1,a2,…,aK}表示一个有限的行为集合，其中K≥2；T=p{si+1|si,ai}是一组状态转移函数，表征了Agent 在状态si下，选择行为ai后转换到状态si+1的过程；R={r1,r2,…,rT}，ri=r(si,ai,si+1)表示关于当前状态、行为和下一个状态的标量函数，即Agent 在状态si下选择行为ai转移到状态si+1后环境给予的奖励。MDP 状态转移过程如图1 所示。

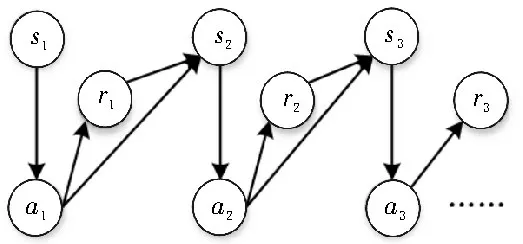
图1 MDP状态转移过程

1.3 离散学习自动机DPRI算法

DPRI算法是强化学习中的一种经典离散学习自动机算法，算法将估计器技术和离散化技术进行了结合[12]。该算法的整体特点是行为选择概率向量的更新取决于环境的反馈和历史经验。算法引入了行为被选择的次数Zi和被奖励的次数Wi，通过求解奖励概率的估计值，追溯奖励概率值最大的行为；行为的累积奖励在区间[0,1]上是跳步更新的，变化量用表示，其中r表示行为的个数，N表示行为概率的更新分辨率。若概率更新后大于1 则强制为1，若更新后的概率值小于0，则强制为0。文中结合强化学习算法的特点，并融合DPRI算法中离散化奖励更新技术，提出了一种基于DPRI的单行为强化聚类算法(Single Behaviour Reinforcement Clustering algorithm based on DPRI，SBRC)。

1.4 ε 贪婪策略

贪婪策略[13]是强化学习中对贪心算法的别称，使用贪婪策略求解问题时，每个阶段达到局部最优解，以实现最终全局最优的目的[14]。文中使用贪婪策略选择行为具体是指，当Agent 选择行为时，选取Q表中累积奖励值最大的行为。ε贪婪策略(0 ≤ε≤1)是基于概率对强化学习任务中的“探索”和“利用”相结合的方法，Agent 每次选择行为时，以ε的概率对Q表进行“利用”，即选择累积奖励值最大的行为，以1-ε的概率进行“探索”，即在行为集中随机选择一个行为。依据3.2 节的实验结果，SBRC 算法中ε取值为0.9。

2 算法实现

文中提出的SBRC算法将ε贪婪策略和DPRI算法的离散化奖励更新技术与聚类算法相结合，把聚类任务转化为强化学习任务。算法初始化时，建立一个大小为N×K的Q表，其中N表示输入样本的数量，对应N个Agent，K表示Agent 可选择的行为数量，对应聚类任务中的聚类数目，Q表中的每一行数据与一个Agent 相关联，算法在迭代过程中不断更新Q表直至趋于稳定。停止迭代时，每个Agent 最大累积奖励所对应的类簇即为该样本的所属类簇。

2.1 强化信号的构建

强化学习中强化信号是环境给与Agent 的反馈信号[15]。传统的K-means 等聚类算法根据聚类中心的变化是否小于给定的阈值作为算法停止迭代的条件，但聚类中心只能反映该类簇在样本空间的位置，无法对类簇中样本的聚集程度进行描述。平均类内距离反映了类簇中样本的聚集程度，若一次迭代结束后平均类内距离增大，则说明该类簇中的样本更加分散，反之则更加紧密。因此，SBRC 算法使用平均类内距离变化趋势作为发送强化信号的依据，平均类内距离的计算方法如式（1）所示：

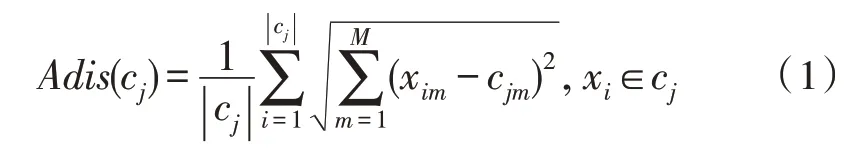
式（1）中，Adis(cj)表示第j个类簇的平均类内距离，|cj|表示第j个类簇中样本的数量，M表示样本的属性个数，xim表示第i个样本的第m个属性，cjm表示第j个聚类中心的第m个属性，其中1≤m≤M。

2.2 Q表的构建

SBRC 算法运行前建立大小为N×K的Q表，如表1 所示，其中rik表示第i个Agent 行为k的累计奖励。该算法无需满足条件,1 ≤i≤N，即去除了Agent 累积奖励和为1 的约束。Q表在算法迭代过程中不断更新，最终达到稳定状态。

表1 输入样本所对应的Q表

2.3 Q表的更新过程

SBRC 算法运行过程中，Agent 根据ε贪婪策略选择行为。每次迭代结束后，计算各类簇的平均类内距离，并与该类簇上一次得到的平均类内距离比较。如果距离减小，则表明此次迭代选择该行为的所有Agent 组成的类簇更加紧密，该类簇中所有Agent 会得到一个奖励信号，使得该行为的累积奖励值增大，反之使得该行为的累积奖励值减小，Q表的更新过程如图2 所示。算法迭代过程中，每个Agent有ε的概率去选择最大累积奖励值所对应的行为，有1-ε的概率在行为集中随机选择一个行为，图2中假设了聚类数K=3 的情况。该更新过程是针对一个Agent 而言的，图中与聚类数对应的行为数为3，分别代表3 个类簇。状态Siter表示该Agent 正处于第iter次迭代，Q1、Q2、Q3分别表示3 种行为的累积奖励，Adis(iter)表示该Agent 所在类簇第iter次迭代结束后的平均类内距离。Q1↑表示行为1 的累积奖励增大，Q1↓表示行为1 的累积奖励值减小，Q1_ 表示行为1 的累积奖励值不变。算法中设置累积奖励上下限分别为1 和-1，如果更新后的累积奖励值大于1或者小于-1，则将其强制为1 或-1。累积奖励的更新方法如式（2）和式（3）所示：

图2 SBRC算法Q表更新过程

式（2）表示Agent 选择了行为k后，相较于上次迭代，平均类内距离减小时累积奖励的更新方式。行为k的累积奖励增大，其余行为的累积奖励不变。

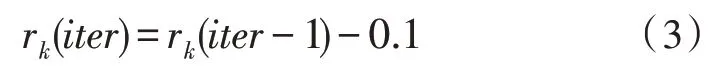
式（3）表示Agent 选择了行为k后，相较于上次迭代，平均类内距离增大时的累积奖励的更新方式。此时行为k的累积奖励减小，其余行为的累积奖励不变。

2.4 算法初始化及伪代码

算法运行前需要输入参数，并对相关变量进行初始化：输入聚类数K，最大迭代数为maxiter，平均类内距离变化阈值为stop；创建大小为N×1 的行为向量，用于存储Agent 选择的行为，初值设置为0；创建大小为N×K的Q表，用于存储累积奖励，初始值设为0；创建大小为N×1 的强化信号向量，用于存储环境反馈的信号，初始值设为0；创建大小为2×K的向量，用于存放平均类内距离，初始值为0。SBRC 算法的伪代码如下：

SBRC 算法第一次迭代时，所有Agent 随机选择一个行为，计算各个类簇的平均类内距离。从第二次迭代开始，每个Agent 依据ε贪婪策略选择行为，并计算新的平均类内距离，与上一次迭代得到的平均类内距离作比较。若距离减小，则给予该类簇中所有Agent 奖励信号，否则给予惩罚信号，每个Agent根据收到的信号类型更新Q表，当平均类内距离的变化小于阈值stop或达到最大迭代次数maxiter，则停止迭代并输出聚类结果。

3 实验及结果分析

3.1 实验数据及评价指标

实验采用准确率、DB 指数以及轮廓系数对聚类性能进行评价。准确率的计算方法如式（4）所示：

式（4）中，n表示样本的数量，ck表示Q表中样本标签为k的所有样本集合，rj表示真实标签为j的样本集合。表示两者交集中样本的数量。

Davies-Bouldin(DB)指数[16]是聚类算法的一种内部评价指标，该值越小表明聚类效果越好，计算方法如式（5）所示：

式（5）中，K为聚类数目，Adisi为类簇Ci的平均类内距离，Cij为类簇Ci和类簇Cj聚类中心之间的距离。

轮廓系数结合了内聚度和分散度两种因素[17]，可以对同一数据集在不同算法中的聚类结果进行评价。轮廓系数的计算方法如式（6）所示：

式（6）中，a(i)为第i个样本与它所属类簇中其他样本的距离均值，b(i)为第i个样本到与之距离最近的另一个类簇中所有样本的距离均值。轮廓系数介于-1 和1 之间，且越接近1，该点的内聚度与分散度越好。

实验数据及Q表初始化值如表2 所示。其中D1～D7 为小规模数据集，D8～D10 为中规模和大规模数据集。

表2 数据集信息及Q表初始化值

3.2 贪婪系数的选取

文中以iris 数据集为例说明贪婪系数的选取过程。使用不同的贪婪系数进行SBRC 聚类，分别取值0.5、0.6、0.7、0.8 和0.9，选取同一样本观察不同贪婪系数下最大累积奖励的收敛情况，实验结果如图3 所示。由图3 可知，贪婪系数为0.5 时Q值的收敛速度最慢，为0.9 时收敛速度最快，对其他数据集进行分析可得到相同结论，因此，将贪婪系数设置为0.9。

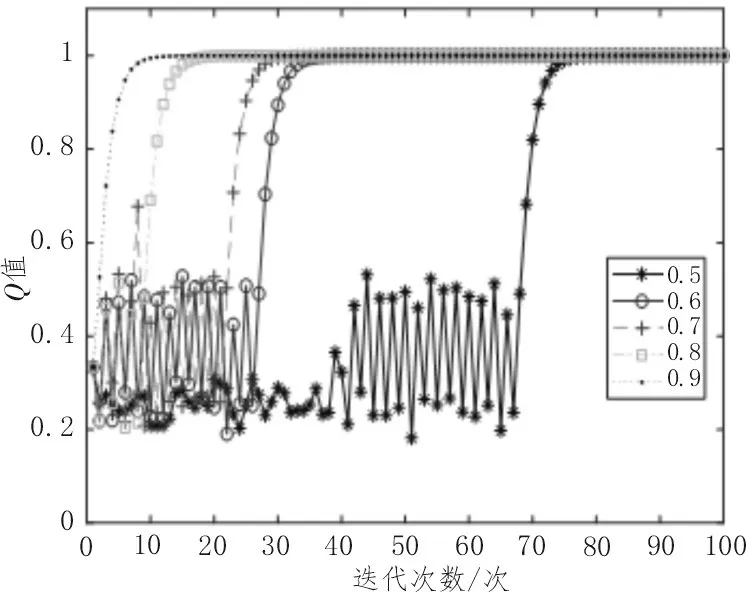
图3 贪婪系数对算法收敛性能的影响

3.3 实验结果及分析

为说明SBRC 算法的有效性，文中选用经典聚类算法K-means（简称KM）、K-means++（简称KM++）、FCM 以及文献[9]提出的LAC 算法作对比，进行聚类性能分析。

图4给出了5种算法平均准确率的对比情况。由图4 可知，相比于其他3 种聚类算法，LAC 和SBRC 算法结果整体最优。10个数据集中有6个数据集SBRC算法的准确率最高，其中D3、D6、D8 数据集的准确率相比于LAC 算法分别提高了1.8%、3.8%和2.6%。

图4 SBRC算法准确率对比结果

图5 给出了5 种聚类算法DB 指数的对比情况。由图5 可知，相对于3 种经典聚类算法，LAC 和SBRC算法结果整体依然较优，且SBRC 算法稍优于LAC。10 个数据集中有6 个数据集SBRC 算法的DB 指数均最优，其余数据集结果也接近最优，这表明SBRC 聚类算法具有较好的类内紧凑度和类间分散度[18]。

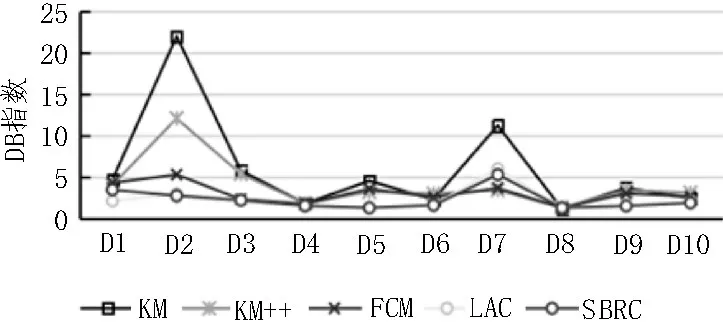
图5 SBRC算法DB指数对比结果

图6 给出了5 种算法轮廓系数的对比情况。由图6 可知，10 个数据集中有5 个数据集SBRC 算法的轮廓系数最高，其中D5、D6、D8 和D10 数据集相比于LAC 算法分别提高了0.018、0.053、0.068 以及0.048。

图6 SBRC算法轮廓系数对比结果

表3 给出了5 种聚类算法运行时间的对比情况。由表3 可知，7 个小规模数据集中，4 个数据集SBRC算法运行时间最短。3 个中规模和大规模数据集相较于其他几种对比算法，LAC 和SBRC 算法的运行时间至少降低了一个数量级，SBRC 算法比LAC 算法降低效果显著。其原因一方面与强化学习的行为选择机制有关；另一方面，由于SBRC 算法采用了单行为奖励方式，其他未选择行为的累计奖励不需要更新，所以相对于LAC 算法，SBRC 算法时间复杂度更低。

表3 SBRC与已有聚类算法运行时间对比情况

综上可知，与3 种经典算法相比，LAC 和SBRC算法在准确率、内聚度和分散度方面，皆具有更优的聚类性能。在算法运行复杂度方面，SBRC 算法使用的单行为奖励更新机制使之具有更低的时间复杂度；对大规模数据集而言，SBRC 算法则具有更强的时间优势。

3.4 实验过程分析

为说明SBRC 算法有效性，对算法迭代过程中单个Agent 累积奖励进行跟踪，说明Q表的更新及收敛情况。图7 给出了iris 数据集中单个样本Q值的更新及收敛情况。其中，图7(a)、(b)、(c)分别取自3 个不同标签中的样本，图中a1、a2及a3分别表示行为1、行为2 和行为3。通过分析可知，图7(a)和图7(c)的收敛速度较快，但是图7(b)中的Q值在算法运行前期经历了一段时间的震荡，这是由强化学习本身“探索”和“利用”的特性以及样本本身的分布情况造成的。

图7 iris数据集每类中单个样本Q值更新及收敛情况

4 结论

针对聚类结果对初始聚类中较为敏感的缺陷以及样本的划分方式对聚类性能的影响，文中提出了一种基于DPRI算法的SBRC 聚类算法。实验结果表明，相比3 种经典聚类算法，文中提出的SBRC 算法及LAC 算法在大多数数据集上具有更高的准确率、更优的DB 指数以及更高的轮廓系数，说明了两种基于强化学习聚类算法的有效性。时间复杂度方面，相比于LAC 算法，SBRC 算法处理各种规模的数据集时，都具有较大优势，这对下一步继续采用SBRC 算法分析大规模数据集，提供了前期研究基础。但是，SBRC 算法通过建立Q表存储各行为的累积奖励，是一种用空间换时间的做法，下一步就如何减小算法的空间复杂度方面进行研究。