基于低轨星载正六边形阵的和差测向算法

程佳琦，赵璐璐，梁 广，余金培

（1.中国科学院微小卫星创新研究院，上海 201203；2.中国科学院大学，北京 100049）

单脉冲和差测向因精度高、计算复杂度低、工程实现容易在测向领域得到了广泛关注和应用。传统的单脉冲和差测向算法主要有3 种：半阵法[1]、直接加权法[2]和双指向法[3]。现有研究表明，直接加权法在鉴角范围和精度以及抗干扰性能上都有明显优势[4]。

平面相控阵常用的栅格排列方式有两种：矩形栅格和三角形栅格。现有研究表明，在阵面口径相同的情况下，采用三角形栅格比矩形栅格可节省约13%的阵元及馈电组件，节约了资源，降低了天线成本；同时三角形栅格阵列具有体积小、辐射效率高等优点，因此，在低轨卫星通信系统中，通常采用基于三角形栅格构成的正六边形平面阵列[5-7]。

传统的和差测向算法通常都是针对矩形栅格的平面阵列，无法直接应用于三角形栅格平面阵列[8-14]，因此研究基于正六边形相控阵的和差测向算法具有重要意义。

1 算法基本原理

星载多波束天线采用37 阵元正六边形相控阵，如图1 所示，阵元采用双层双馈微带天线，仿真示意图如图2 所示。

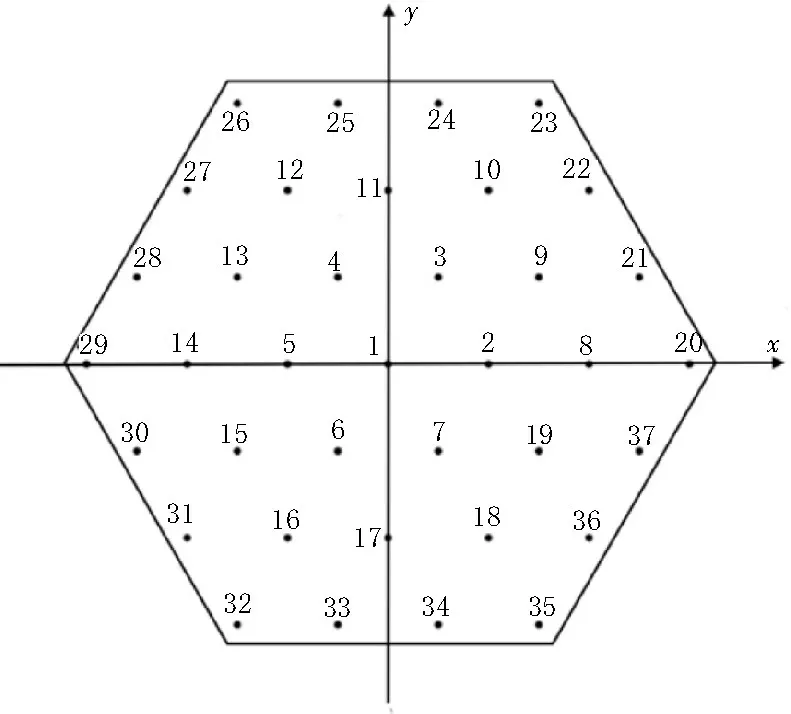
图1 正六边形相控阵示意图

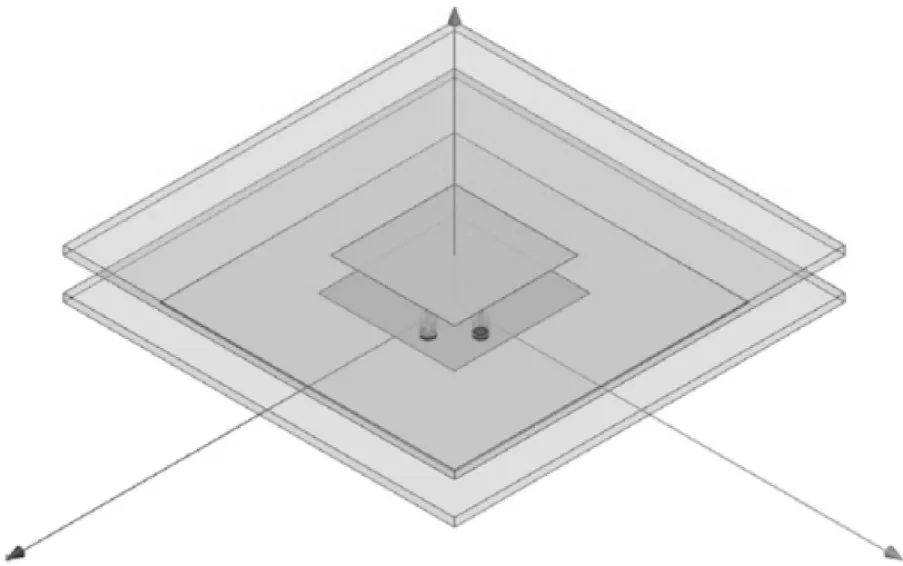
图2 双层双馈微带阵元天线仿真示意图

图3 所示为角度解算模型示意图，该模型共有3条对角线l1、l2和l3，三条对角线的交于点O，信号来向为OP方向，OP在l1与l2所在面上的投影为OM。记l1与OP方向夹角为θ1，l2与OP方向夹角为θ2（图中未标注），所求方位角φ为l2与OM方向的夹角，俯仰角θ为Z轴与OP方向的夹角。

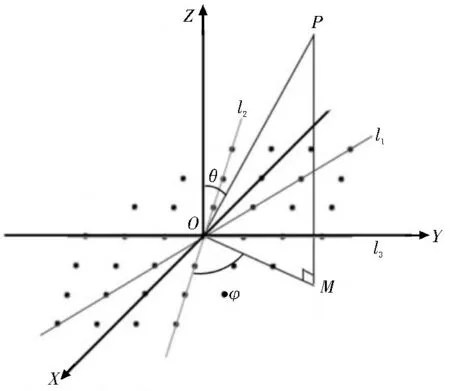
图3 角度解算模型示意图

首先选取l1和l2两条对角线作为测角方向，在两个方向上分别进行直接加权法和差测角，得到两个方向上的来向角θ1、θ2，然后进行二维角度计算。

由三余弦定理可得：

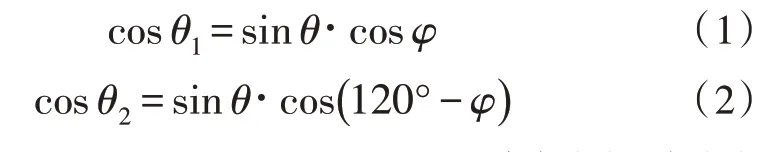
令u=sinθ·cosφ,v=sinθ·sinφ，则式（1）、式（2）可转化为：

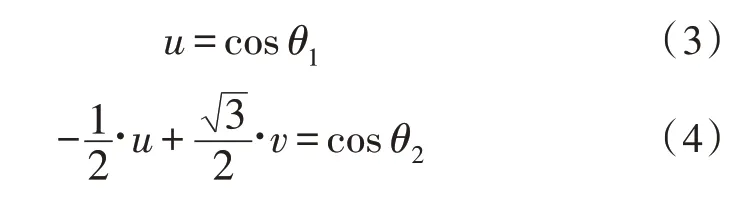
联立可得：

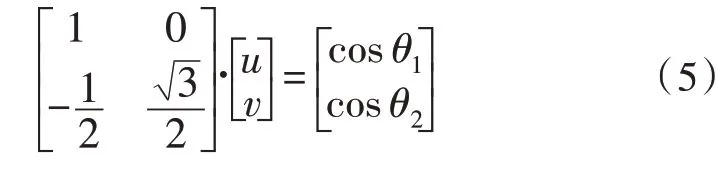
求解上式可得：

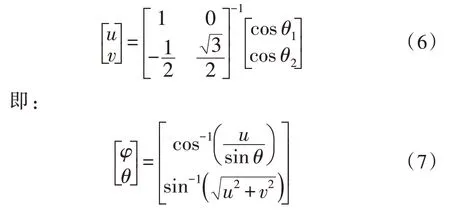
2 算法优化

2.1 鉴角曲线分段处理

传统斜率法采用1 段式线性拟合，拟合偏差较大，从而影响鉴角精度，对此，提出分段拟合的算法，从而实现更高精度的一维和差测向。

假设采用均匀线阵，阵元数N=7，阵元间距，旁瓣抑制数=5，主副瓣电平比R0dB=30，引导角θ0=20°。当固定信噪比为0 dB 时，不同分段处理方法对不同偏角测量精度的影响如图4 所示。从图4 可以看出，分段处理斜率法相比传统1 段式斜率法的鉴角误差有明显降低，且分段数越多，鉴角误差越小。

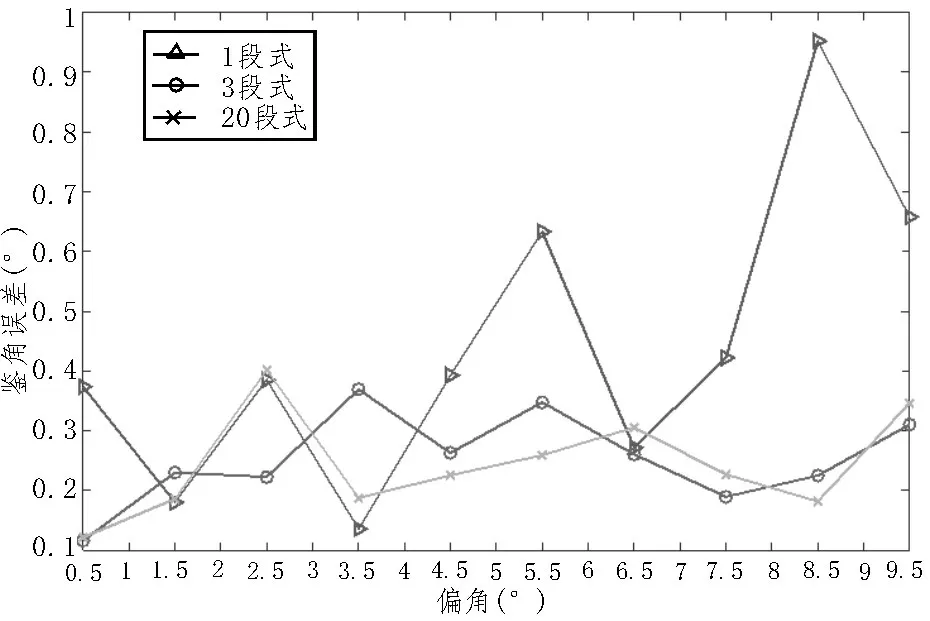
图4 不同分段处理方法对不同偏角测量精度的影响

当固定偏角为6.5°时，信噪比对直接加权法测量精度的影响如图5 所示。从图5 可以看出，在不低于-14 dB 的低信噪比环境下，分段处理斜率法比传统1 段式斜率法性能更好、精度更高。

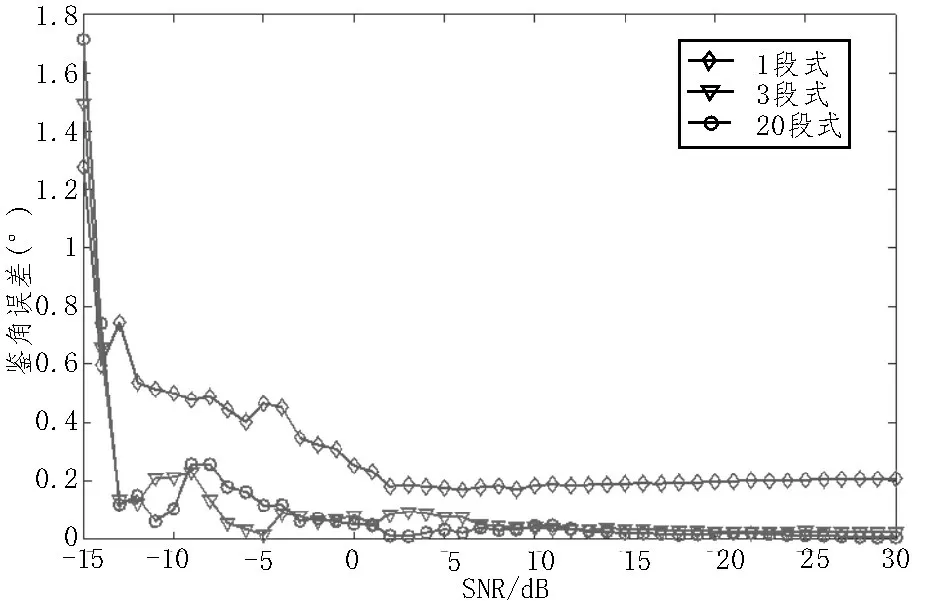
图5 信噪比对直接加权法测量精度的影响

通过3 段式分段处理和20 段式分段处理的仿真结果对比可以看出，当段数从3 段增加到20 段时，图4 所示鉴角误差直观上区别不明确，通过仿真计算，平均鉴角误差仅降低0.01°。如图5 所示，两者性能相近，但20 段式分段处理算法的复杂度明显高于3 段式分段处理算法。在实际应用中，卫星上的运算资源非常宝贵，因此，综合考虑精度及复杂度要求，最终算法采用3 段式分段处理。

2.2 误差校正处理

为了进一步提高算法精度，引入第三条对角线l3，构建超定方程组，并利用最小二乘法求解[15-16]，以降低误差。

对l3方向进行一维和差测角，得到偏角θ3。根据前文所述算法基本原理，可得：

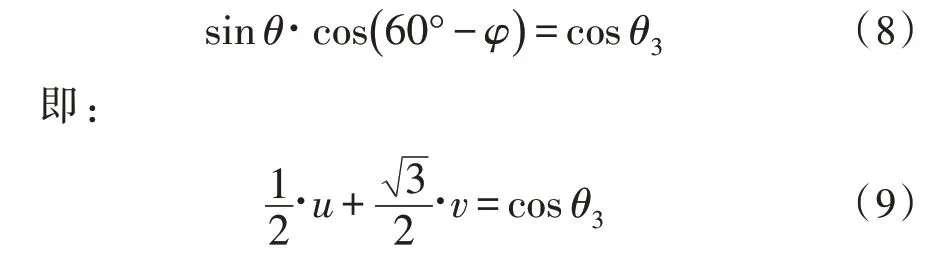
将式（9）与式（3）、式（4）联立，得超定方程组：

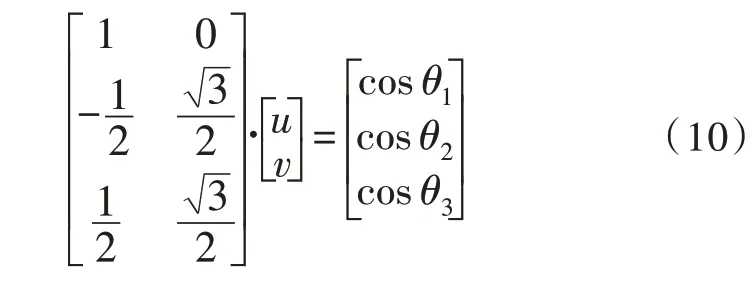
记为AX=b，其中：

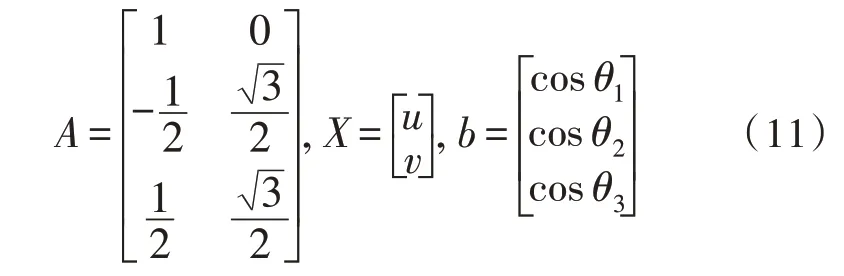
利用最小二乘法求解可得：

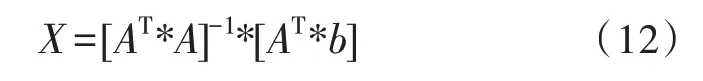
再利用式（7）即可得方位角φ和俯仰角θ。

3 仿真试验及结果分析

3.1 算法在不同偏角下的鉴角误差

仿真条件：阵元分布为37 阵元正六边形三角形栅格相控阵，如图1 所示，阵元间距，旁瓣抑制数=5，主副瓣电平比R0dB=30，引导角(φ0,θ0)=(45°,45°)，信噪比为0 dB。

3.2 算法在不同信噪比下的鉴角误差

仿真条件：阵元分布为37 阵元正六边形三角形栅格相控阵，如图1 所示，阵元间距，旁瓣抑制数=5，主副瓣电平比R0dB=30，引导角(φ0,θ0)=(45°,45°)，偏角为(4.5°,4.5°)。

3.3 结果分析

综合图6、图7 及图8、图9 所示仿真结果，所提优化后算法在信噪比大于-10 dB 的环境中，方位角鉴角误差稳定，不超过1.2°，俯仰角鉴角误差稳定，不超过0.8°，可以有效实现DOA 估计。

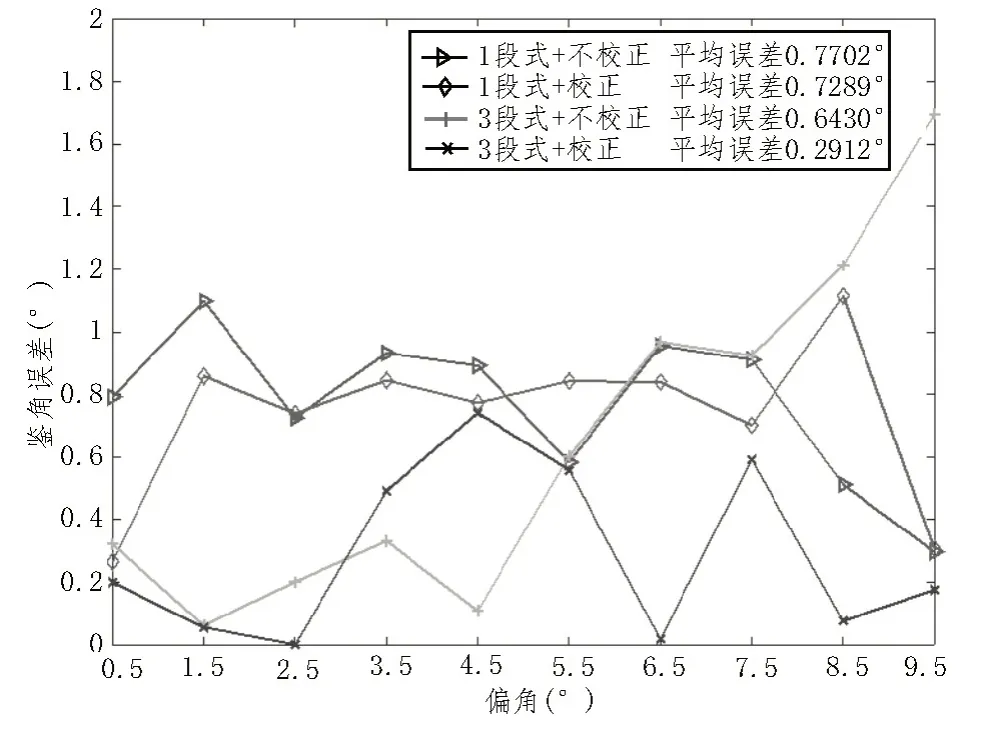
图6 方位角鉴角误差随偏角变化曲线图

图7 俯仰角鉴角误差随偏角变化曲线图

通过图8 及图9 中4 种算法随信噪比变化的仿真结果对比可知，对于方位角，利用3 段式进行一维和差测向的算法在低信噪比环境中，平均误差降低了0.3°。而对于俯仰角，采用同等分段法进行一维和差测向的情况下，利用误差校正的算法在低信噪比环境中算法误差比未校正原始算法低了近0.7°，可见分段算法及误差校正算法对于算法在低信噪比环境下的性能提升有显著效果。

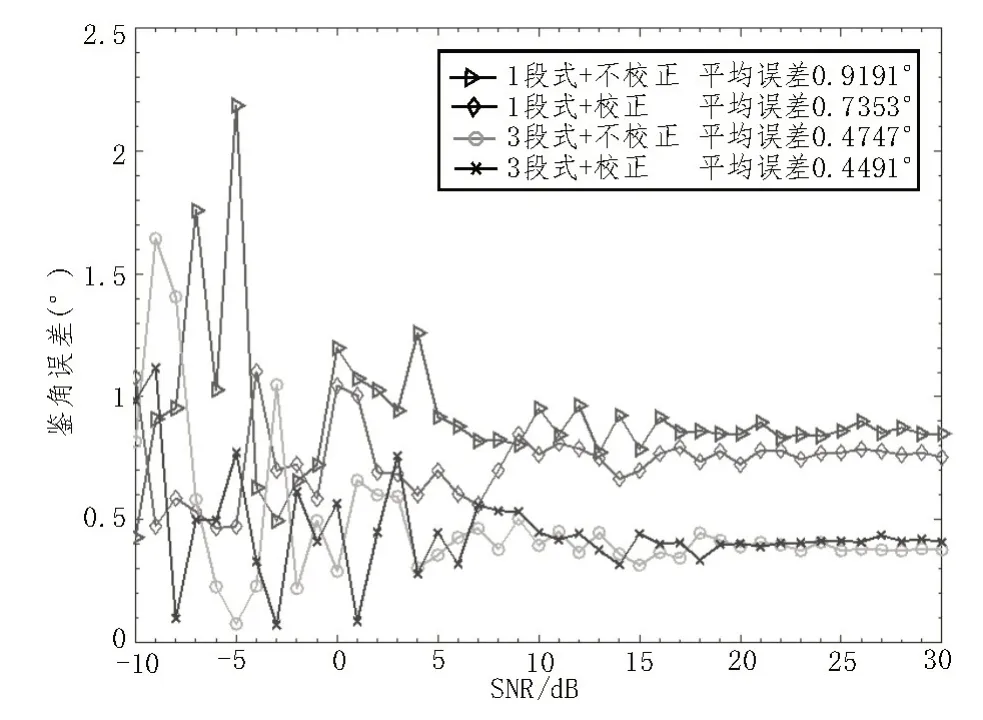
图8 方位角鉴角误差随信噪比变化曲线图

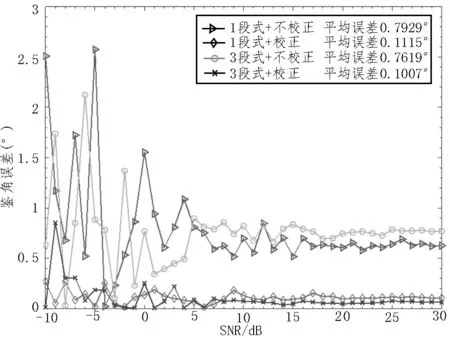
图9 俯仰角鉴角误差随信噪比变化曲线图

综上，文中优化后的算法因具有精度较高、低信噪比环境中稳定性好的优点，具有一定的工程应用价值。

4 结束语

文中以提出适用于低信噪比环境中应用于正六边形相控阵的较高精度DOA 估计算法为目标，基于一维和差测角算法，利用分段处理算法，提高了一维测角算法精度。通过仿真验证，对比传统直接加权算法，利用分段处理算法后，鉴角误差明显降低。同时，利用最小二乘法求解超定方程的误差校正算法，使基于正六边形相控阵的二维解算算法适用于低信噪比环境。通过仿真验证，使用分段校正算法后，算法在低信噪比环境中的鉴角误差明显降低且稳定性较高。仿真结果表明，在大于-10 dB 的低信噪比环境中，方位角鉴角误差稳定，不超过1.2°，俯仰角鉴角误差稳定，不超过0.8°，可以有效实现DOA 估计，仿真结果验证了算法的有效性及实用性，对工程应用有一定的参考意义。