小跨高比RPC连梁抗震性能的正交数值模拟
2022-06-29夏鑫韩旭
夏鑫, 韩旭
(1.山东建筑大学 土木工程学院,济南 250101; 2.山东高速股份有限公司 泰东运管中心,山东 泰安 271000)
0 引 言
在剪力墙结构中,剪力墙由连梁和墙肢组成。当地震发生时,剪力墙结构可以承担水平作用力,是目前高层建筑中常见的结构形式之一。在结构抗震设计时,连梁是第一道防线,连梁屈服后在墙肢两端形成塑性铰,耗能效果显著。但是,在实际工程中,受限于建筑、设备等方面的使用要求,连梁多数为小跨高比形式(跨高比<2.5),这导致剪力墙在地震作用下常出现以剪切变形为主的脆性破坏,不能发挥预期作用,无法满足小跨高比连梁的抗震性能要求。
为改善小跨高比连梁的抗震性能,相关学者展开大量研究:傅剑平等改变连梁内部的配筋方式,将菱形配筋与对角斜筋综合配置,使连梁延性和承载性能均得到明显改善;李勇收集国内外82根小跨高比混凝土连梁试验数据,通过数据库分析推导普通配筋与对角斜筋连梁的恢复力模型;SEO等采用水平配筋代替斜向配筋,发现仅有水平钢筋时连梁具有一定的变形能力,但能量耗散水平较低。因此,通过改变配筋方式,可使连梁内力在地震作用下产生重新分布,从而提高其抗震性能。
在标准养护条件下,活性粉末混凝土(reactive powder concrete, RPC)材料构件微观结构致密,抗拉强度可达到10~20 MPa,抗折强度为30~60 MPa,并且在低抗氯离子扩散和冻融性能方面表现优异。采用RPC材料浇筑的连梁,具有强度高、耐久性好等优势,可以解决普通混凝土连梁抗拉强度小、耐久性差和韧性不足等问题。钢纤维的“桥连”作用可提供抗拉承载力,限制裂缝的发展,提高试件的延性,从而提高小跨高比连梁的抗震性能。
为更深入研究小跨高比RPC连梁的抗震性能,利用Abaqus软件模拟其在低周往复加载作用下的力学性能。将模拟结果与现有的试验结果进行对比,说明材料本构关系的合理性。建立9个有限元模型,对跨高比、配筋方式和箍筋量3个因素开展正交分析,探查RPC连梁在地震作用下的破坏过程、变形能力和抗震耗能能力等。
1 RPC连梁抗震性能的正交试验设计
在考虑跨高比、配筋方式和配箍量3种影响因素的基础上,对小跨高比RPC连梁在低周往复加载作用下的受力变形和性能退化进行正交试验,采用极差分析法研究正交试验的结果,其计算公式为
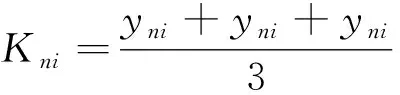
(1)
式中:为因素在水平下得到的结果的平均值;为在因素在水平下的计算结果。在本文分析中,取、和,分别表示跨高比、配箍量和配筋方式,的取值范围为1~3。
利用极差分析可以得到各因素对试验结果的影响程度:在各因素所选用的范围内,极差越大代表此因素水平改变带来的影响越大。试验采用1.00、1.25和1.50等3种较小的跨高比;配箍量取C8@100、C8@75和C8@50等3种;配筋设计菱形配筋方式、对角斜筋配筋方式(见图1)和普通配筋方式等3种。各因素水平的正交试验设计参数见表1。
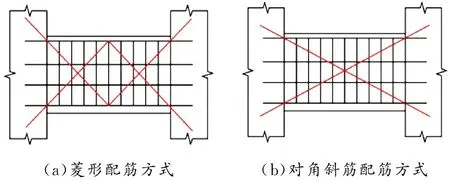
图 1 连梁配筋方式示意
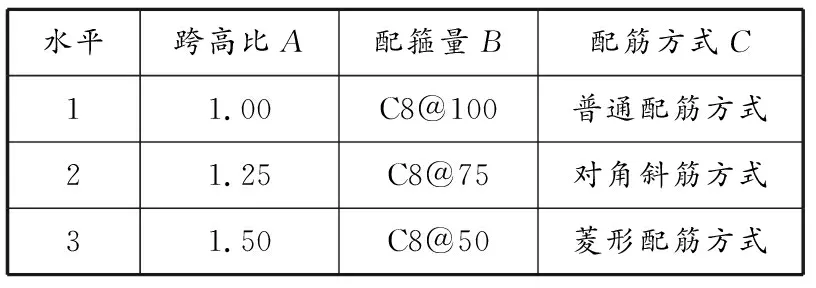
表 1 正交试验设计参数
设各因素之间并无交互作用,3水平3因素情况下的正交试验最少为9次,各水平因素下的试验构件设计参数见表2。
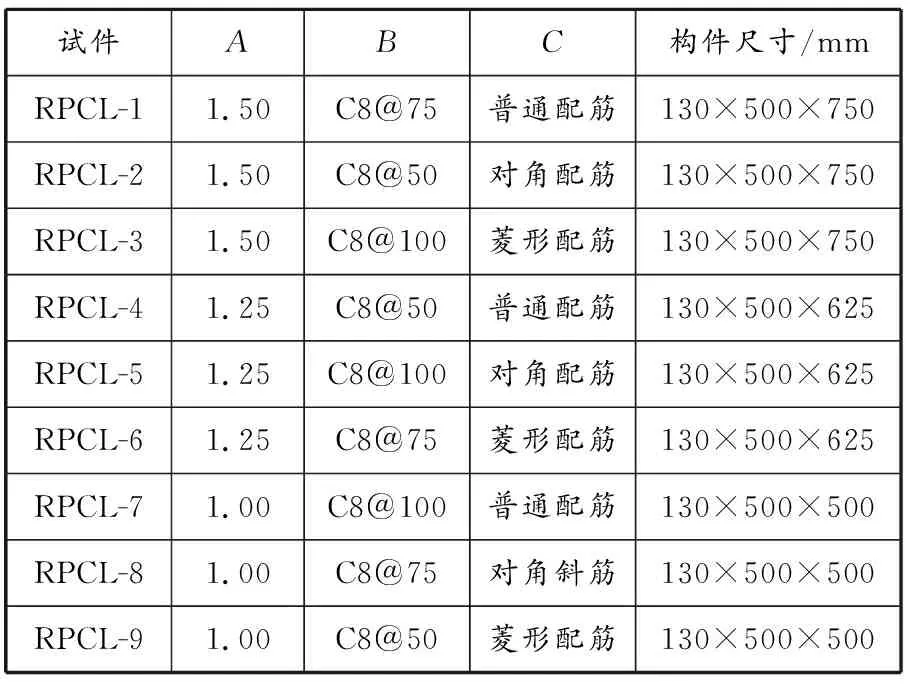
表 2 正交试验构件设计参数
对跨高比、配箍量和配筋方式等3个影响因素的不同水平进行组合,利用正交试验,在有限的试验次数下,得到各设计参数对RPC连梁抗震性能的影响程度。
2 RPC连梁有限元模型
2.1 材料本构关系
2.1.1 RPC本构关系
RPC拉、压性能的差异和RPC损伤可导致刚度退化,因此RPC采用Abaqus内置的塑性损伤模型模拟,其受拉上升段和受压下降段的本构关系通过分段函数表示。
根据文献[11],RPC受压下降段本构关系为
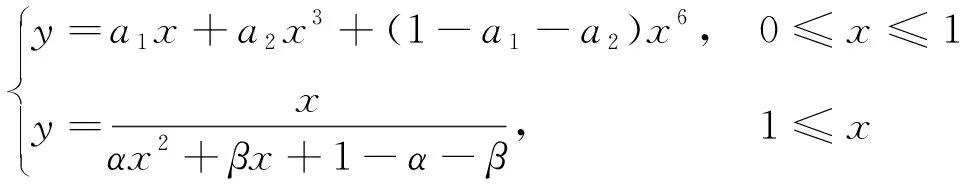
(2)
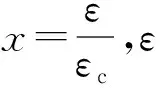
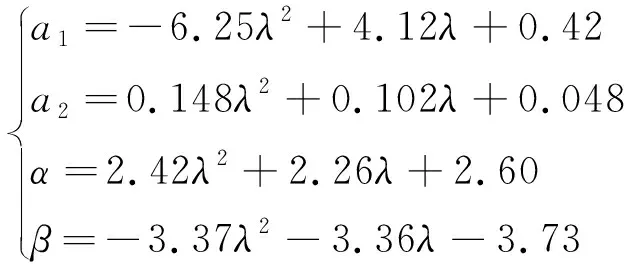
(3)
根据文献[12],RPC受拉上升段的本构关系为
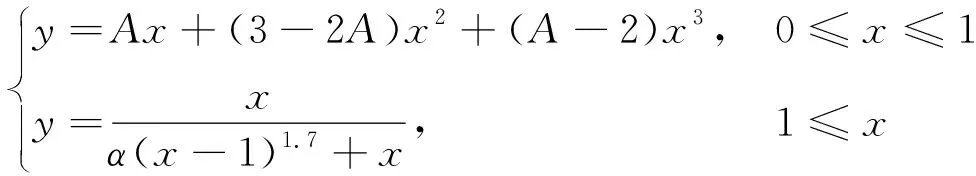
(4)
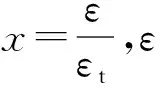
RPC损伤塑性模型的单轴应力-应变关系见图2。
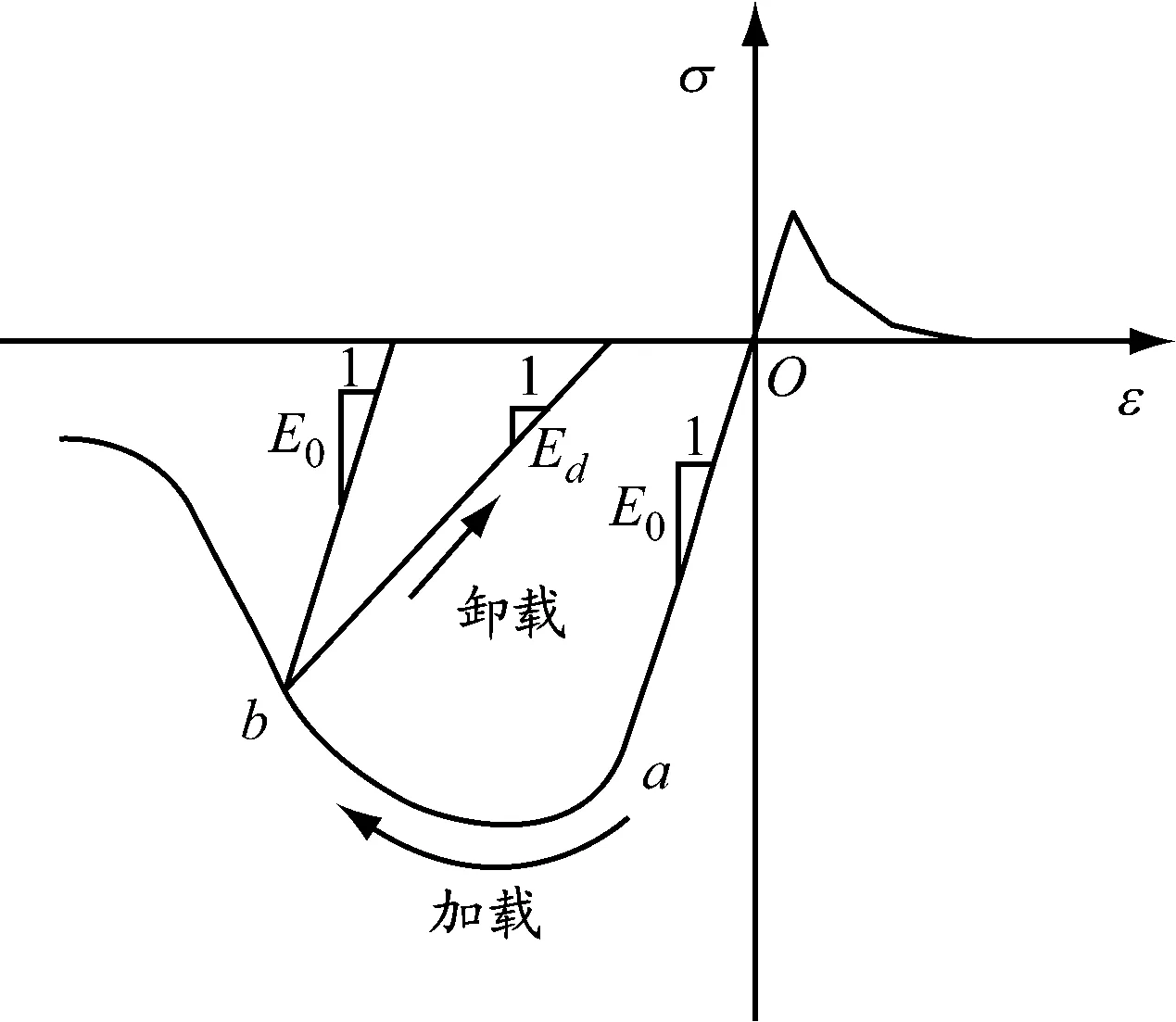
图 2 RPC单轴应力-应变关系
RPC单轴应力-应变曲线大致分为2个阶段:段为加载初期,曲线呈线性分布,即为弹性阶段,应力-应变关系可表示为=;段为塑性阶段,裂缝损伤出现不可恢复的塑性变形,同时刚度开始退化,其弹性模量=(1-),其中为RPC的损伤系数。由Lemaitre的损伤因子理论和Sidiroff能量等价理论,RPC的损伤系数
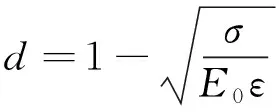
(5)
式中:为RPC构件的应力;为RPC构件应变;为RPC构件弹性阶段的弹性模量。
结合文献[15],可得到RPC的弹塑性参数,见表3,其中=为双轴受压强度与单轴受压强度之比;为应力不变量之比。
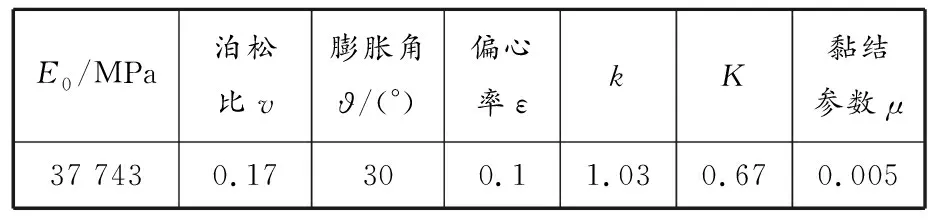
表 3 RPC的弹塑性参数
212 钢筋本构关系
HRP400钢筋采用弹塑性强化本构关系进行模拟,其应力-应变关系可用分段函数表示,即
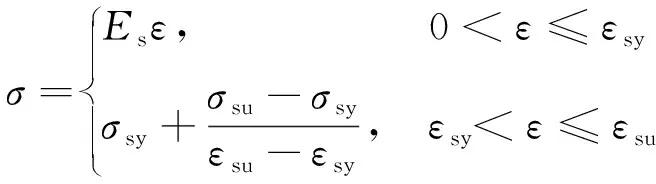
(6)
式中:为拉应力;为拉应变;为屈服应力;为屈服应变;为极限拉应力;为极限拉应变;为弹性模量。钢筋应力-应变曲线见图3。
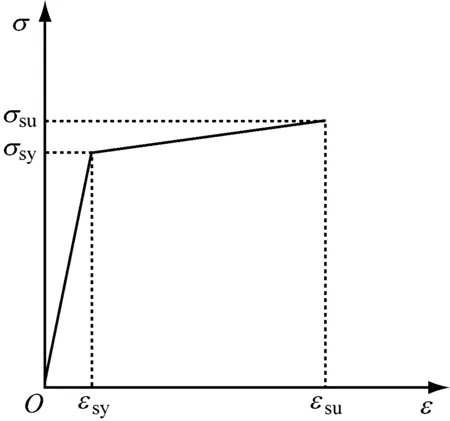
图 3 钢筋应力-应变曲线
213 非线性弹簧本构关系
当地震发生时,RPC与钢筋之间的变形并不协调,甚至会产生黏结滑移现象。在Abaqus建模过程中,采用Spring2非线性弹簧单元模拟接触非线性特征。在钢筋与RPC的接触点布置弹簧单元(见图4),弹簧单元沿钢筋纵向为非线性,无具体尺寸。试验模拟时,每个节点的3个自由度方向均布置弹簧单元。
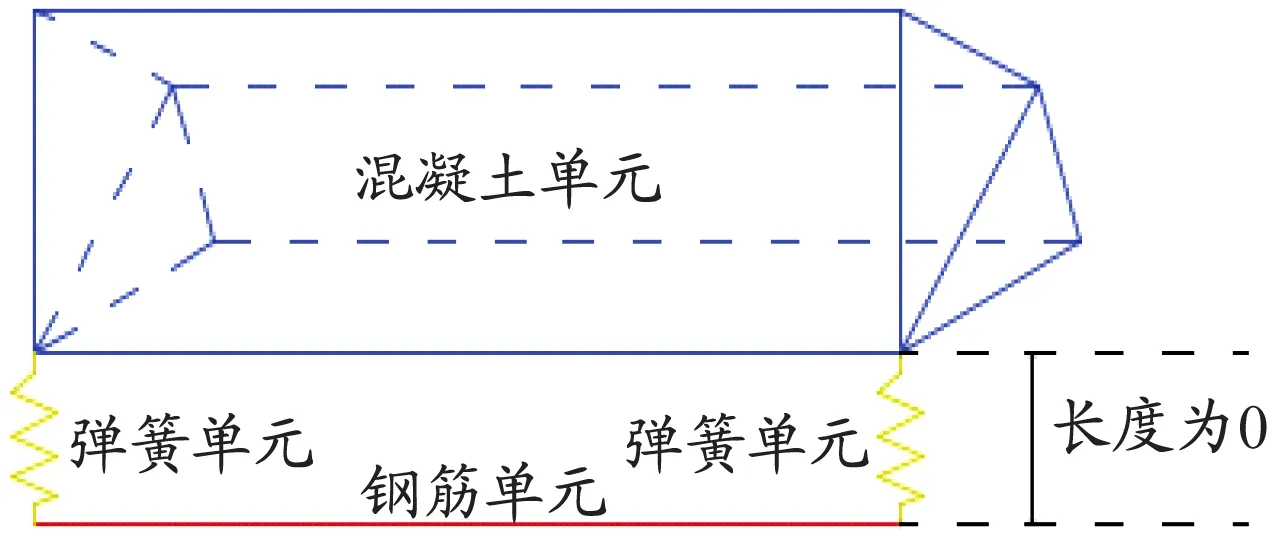
图 4 某一自由度方向非线性弹簧连接RPC与钢筋示意
根据文献[16],钢筋与RPC之间黏结剪应力与相对位移的本构关系为
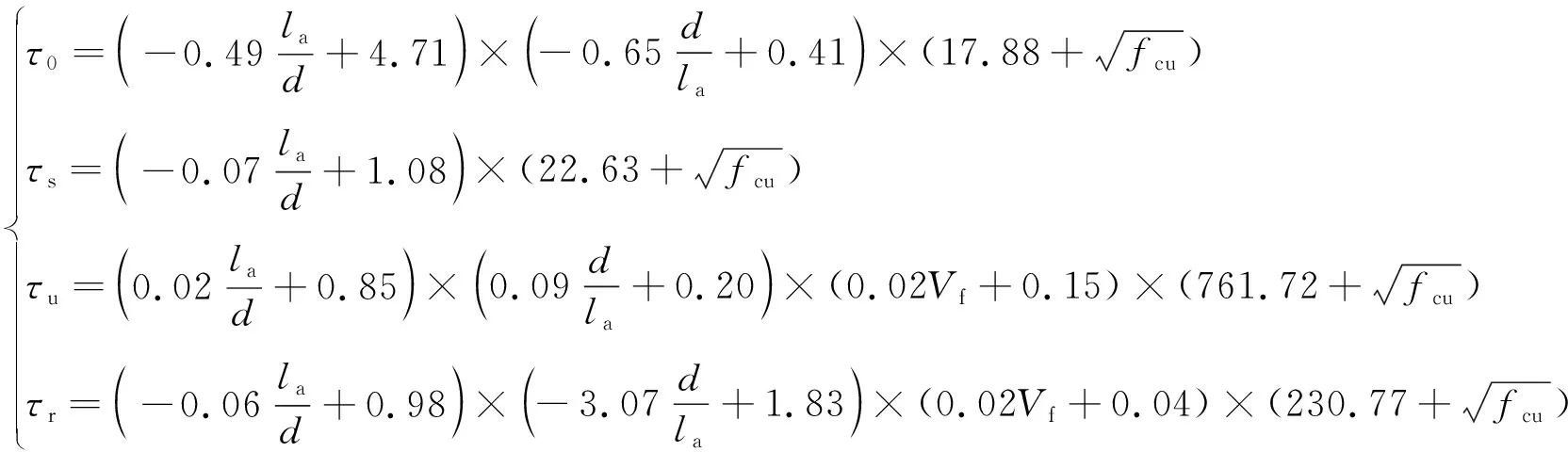
(7)
式中:为钢筋与RPC间的初始黏结强度,MPa;为劈裂黏结强度,MPa;为极限黏结强度,MPa;为残余黏结强度,MPa;为弹簧单元作用长度,mm;为钢筋直径,mm;为钢纤维的体积率;为RPC轴心抗压强度,本文取110 MPa。
根据文献[17],钢筋与RPC间黏结力与相对位移的关系为
=π
(8)
式中:为钢筋与RPC之间的黏结力,N;为被换算的黏结剪应力,MPa。
2.2 本构关系验证
以文献[18]的RPC连梁为模型,展开正交试验模拟,试验装置及内力分布示意见图5。
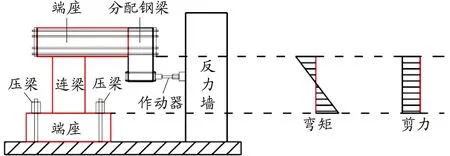
图 5 试验装置及内力分布示意
选取文献[18]中的构件LL-3进行数值模拟,验证第2.1节中材料本构关系的准确性。构件尺寸为130 mm×500 mm×625 mm,其内部钢筋配置为:纵筋4C18,腰筋4C12,双肢箍筋C8@100。构件的具体尺寸及截面配筋示意见图6。根据文献[18]进行RPC连梁抗震性能试验,采用逐级循环加载,加载制度示意见图7。按照上述材料的本构关系建立模型,模型构件尺寸和加载方式与试验保持一致,最终得到构件LL-3的有限元模型见图8,试验与模拟的滞回曲线对比见图9。试验与模拟的滞回曲线趋于一致,说明模型与试验吻合较好。由此可以证明第2.1节中材料的本构关系可行,可在此基础上开展RPC连梁的正交试验数值模拟分析。
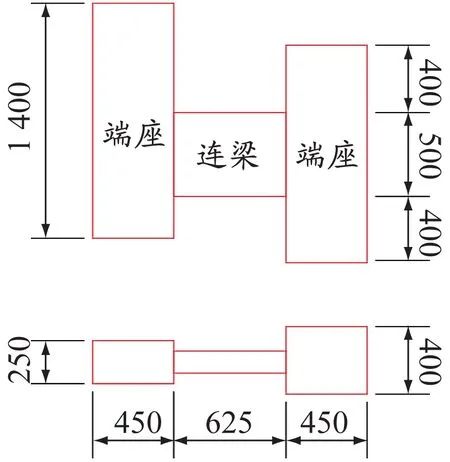
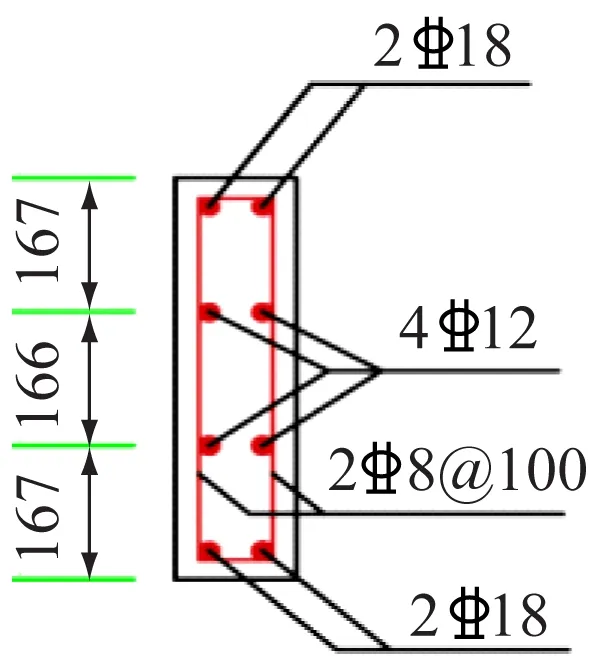
图 6 构件LL-3尺寸及截面配筋方示意,mm
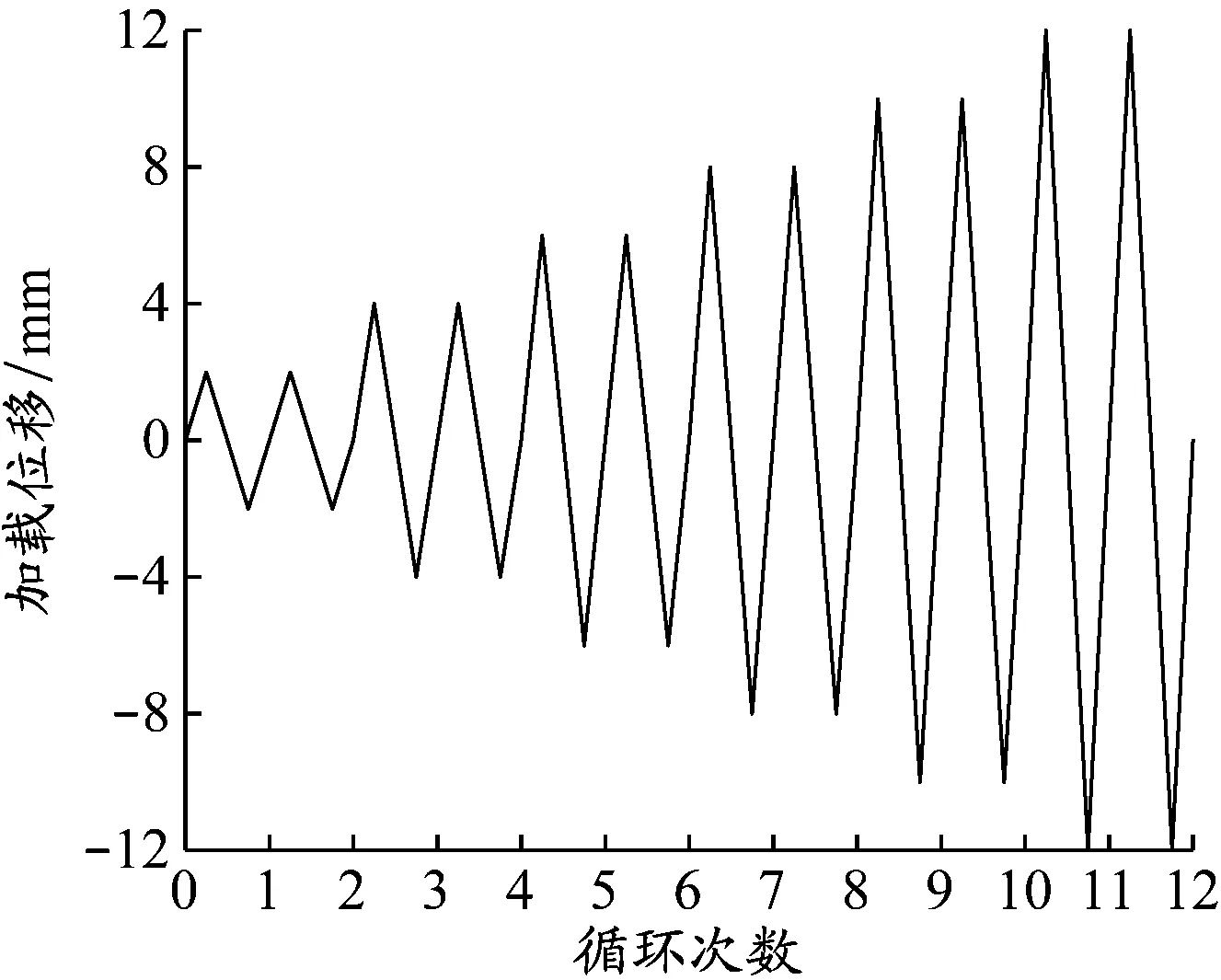
图 7 加载制度示意

图 8 LL-3有限元模型示意
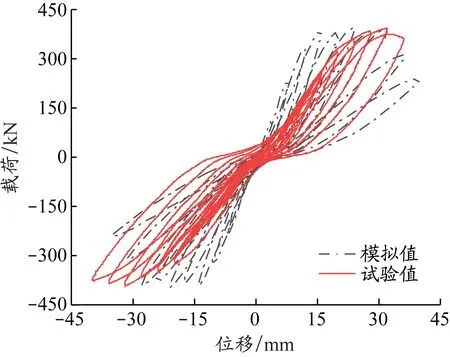
图 9 试验与模拟的滞回曲线对比
2.3 计算模型建立
为研究跨高比、配箍量和配筋方式对RPC连梁抗震性能的影响,以文献[18]的试验为基准,利用Abaqus对RPC连梁进行分离式建模,采用低周往复加载方式,按表2建立9个连梁构件的模型进行正交试验数值模拟。
试验加载简图见图10(a)。为简化模型、提高数据的收敛性,模拟加载去掉分配钢梁,连梁两段采用固接并在一侧施加载荷,简化后的加载方式见图10(b)。
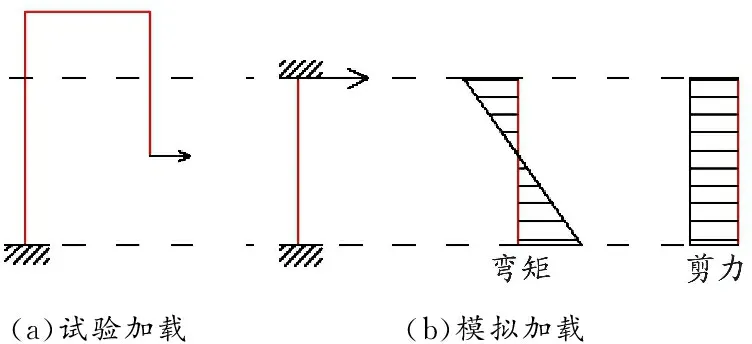
图 10 加载简图
2.3.2 单元选取、边界条件及网格划分
RPC和端座为实体部件,单元类型选择三维8节点减缩积分实体单元C3D8R;钢筋为线部件,需考虑轴向力,因此采用三维2节点桁架单元T3D2模拟,在保证结果准确的同时可提高计算速度。RPC与钢筋之间通过设置非线性弹簧单元连接。
由图10(b)可以确定,RPC连梁底部为固定约束,顶部除允许横向位移外其他方向位移和转动全部施加约束。此外,设置耦合点RP-1、RP-2和RP-3控制构件的约束和加载。
为保证模拟准确的同时减小运算量,RPC连梁分割为较密的小网格,端座位置设置为大网格单元。构件的网格划分见图11。
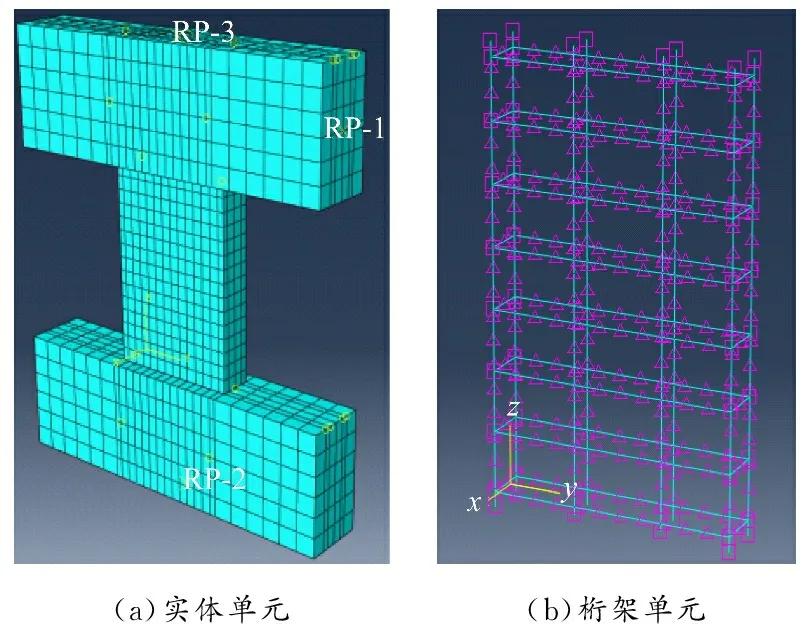
图 11 RPC连梁有限元模型
3 有限元模拟结果分析
3.1 低周往复加载试验结果
9个试验模型的模拟滞回曲线见图12~20。滞回曲线可体现构件在低周往复载荷作用下发生刚度和强度退化以及能量耗散等性能。配筋方式为普通配筋的构件RPCL-1、RPCL-4和RPCL-7表现出明显的剪切破坏,对角配筋、菱形配筋表现为弯剪破坏。根据模拟滞回曲线,得到9个试验模型的峰值载荷、峰值位移、极限位移和最大耗能量,见表4。
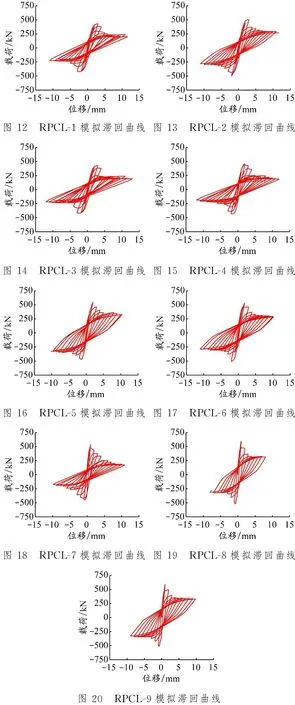
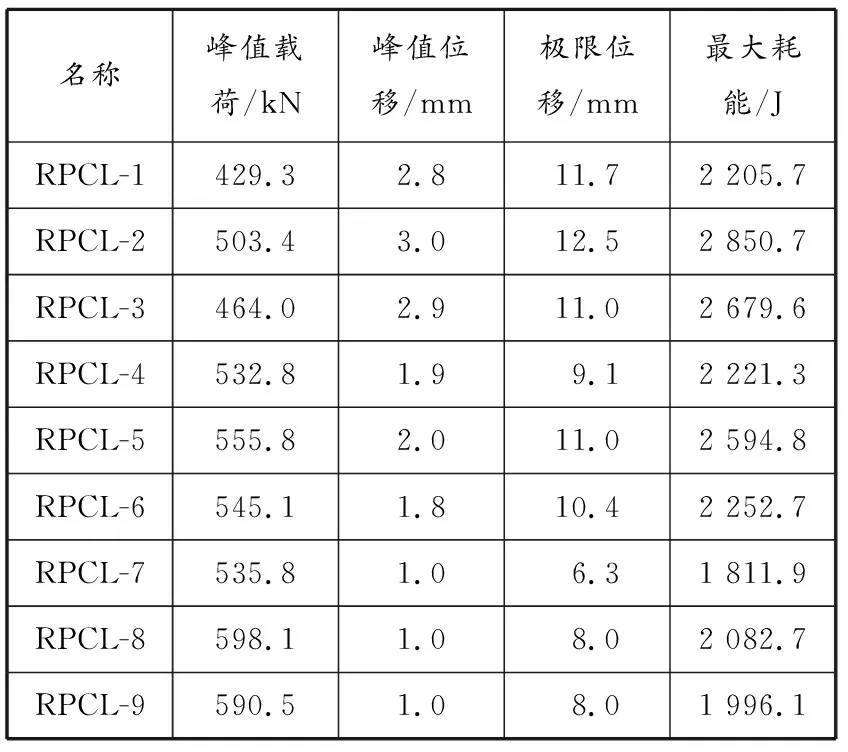
表 4 9个试验模型的模拟结果汇总
3.2 试验分析
3.2.1 钢筋应力
RPC连梁构件屈服、破坏时钢筋的VON MISES应力分别见图21和22。
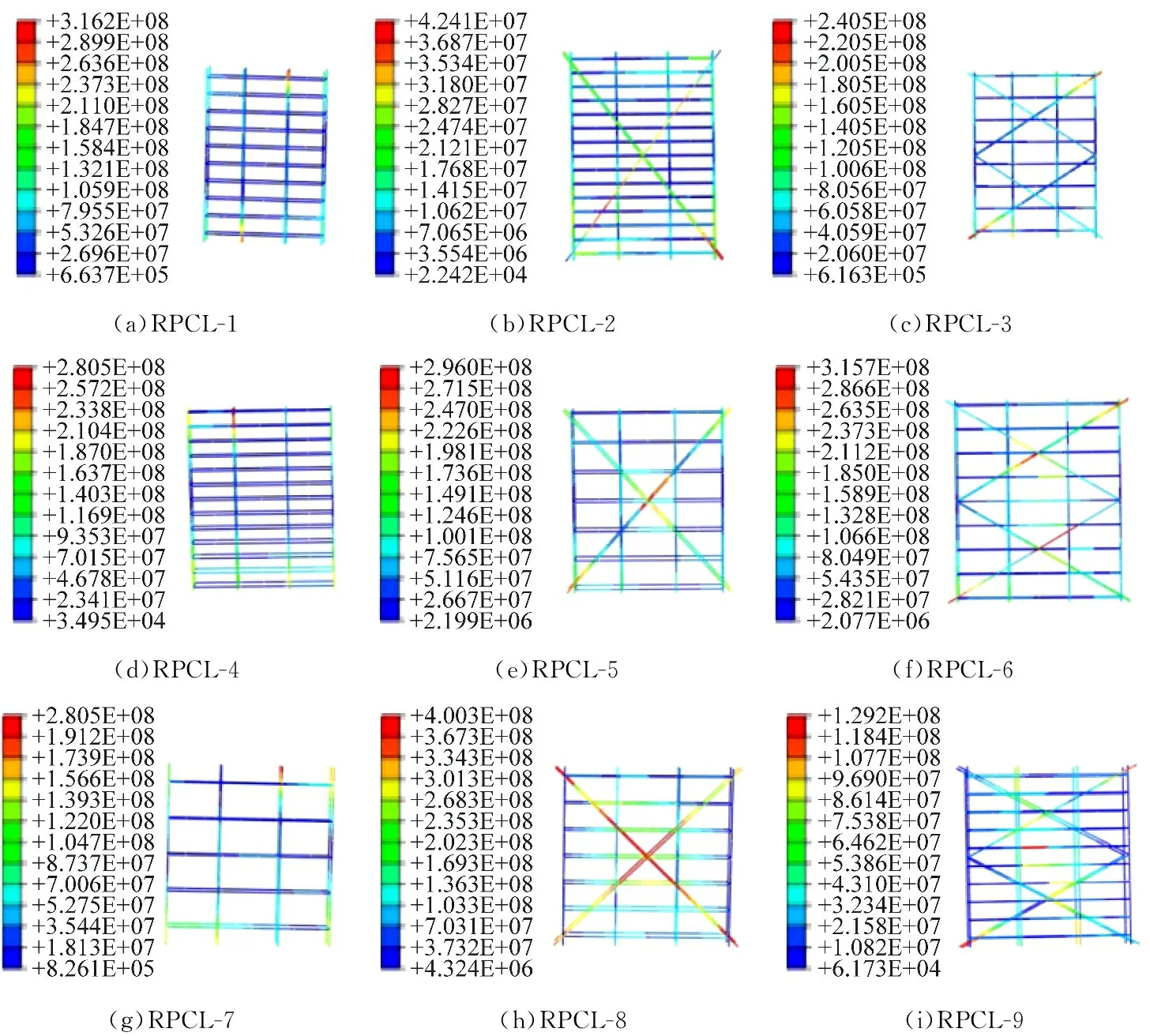
图 21 钢筋屈服应力云图,Pa
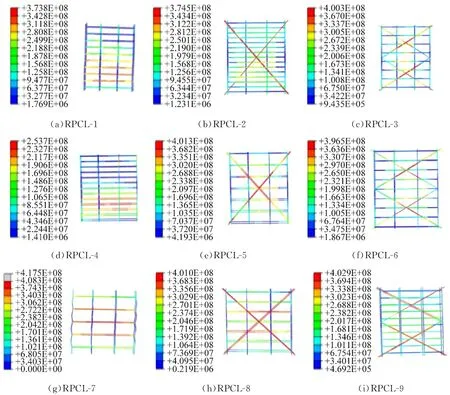
图 22 钢筋破坏应力云图,Pa
初始加载时,RPC应力较大,钢筋几乎不承担内力,构件主要为弯曲变形;随后,构件表面出现裂缝,钢筋应力逐渐增大;构件破坏时,纵筋没有屈服,但跨中位置应力较大,表现为剪切破坏特征。
箍筋量较多的构件破坏时,箍筋没有达到屈服强度;随着配箍量减少,各个箍筋承担的内力增大,最终箍筋屈服。
配筋方式为对角斜筋和菱形配筋时,斜线钢筋总是早于箍筋屈服,构件出现剪压破坏。菱形配筋方式会出现内力重新分布,抗震性能相对较差。
3.2.2 刚度退化
利用环化刚度法得到RPC连梁9个构件的刚度退化情况,见图23,分析各设计参数对刚度退化的影响。当RPC连梁构件的跨高比为1.0时,刚度退化速度最快,且小位移加载时构件就达到屈服;随着跨高比增大,刚度退化速度减缓,表现出良好的延性。不同配筋方式构件的刚度退化由快到慢依次为普通配筋、菱形配筋、对角斜筋;配箍量对刚度影响不明显。RPC连梁设计时,应尽量选择跨高比大、对角斜筋的方式,此时抗震性能更好。
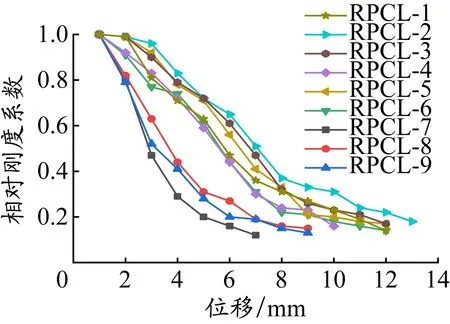
图 23 刚度退化曲线
3.2.3 承载能力
计算各因素下对RPC连梁的承载力,结果见表5。跨高比对连梁承载力影响最大,配箍量的影响最小。9个RPC连梁构件在不同影响因素下的承载力分布见图24。在一定范围内,随着跨高比增大,构件承载力降低;箍筋量的变化对承载力影响无明显规律;斜角配筋方式的构件承载力普遍较高。
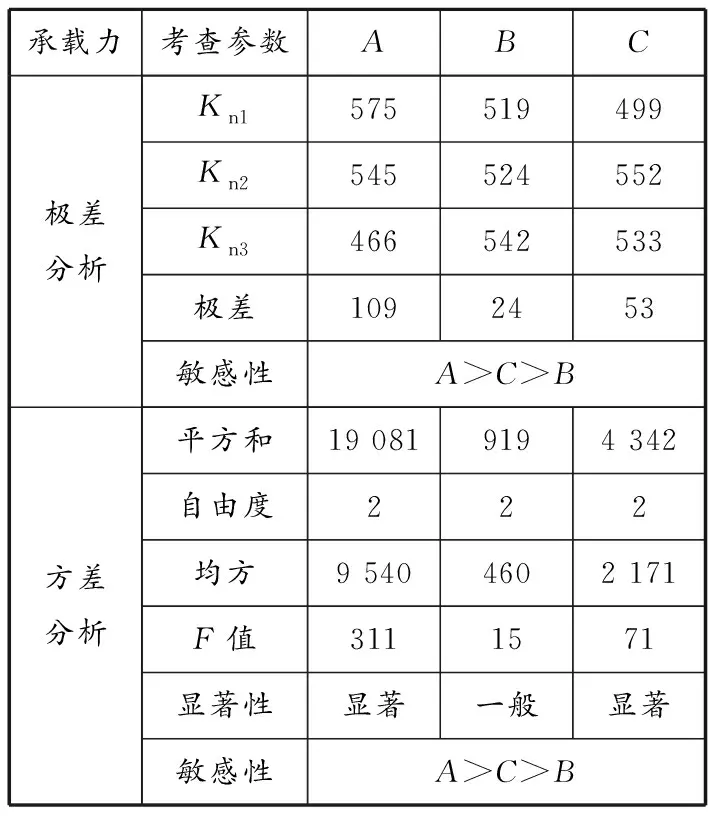
表 5 连梁构件承载力分析结果
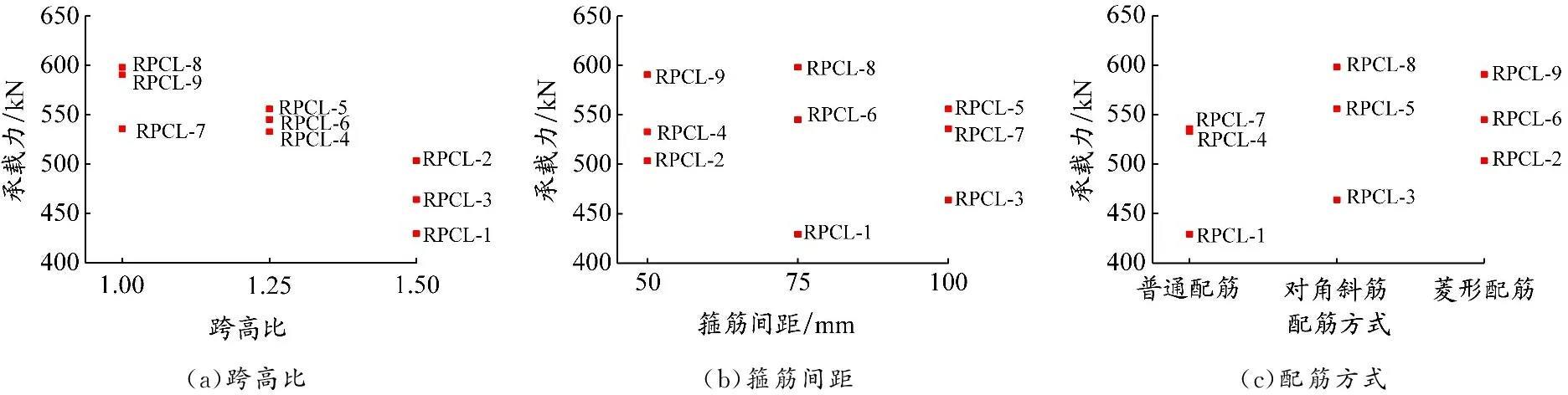
图 24 不同影响因素下连梁构件的承载力分布
3.2.4 变形能力
计算得到各因素对RPC连梁极限位移的影响,结果见表6。跨高比对RPC连梁变形能力影响最大,配箍量影响最小。
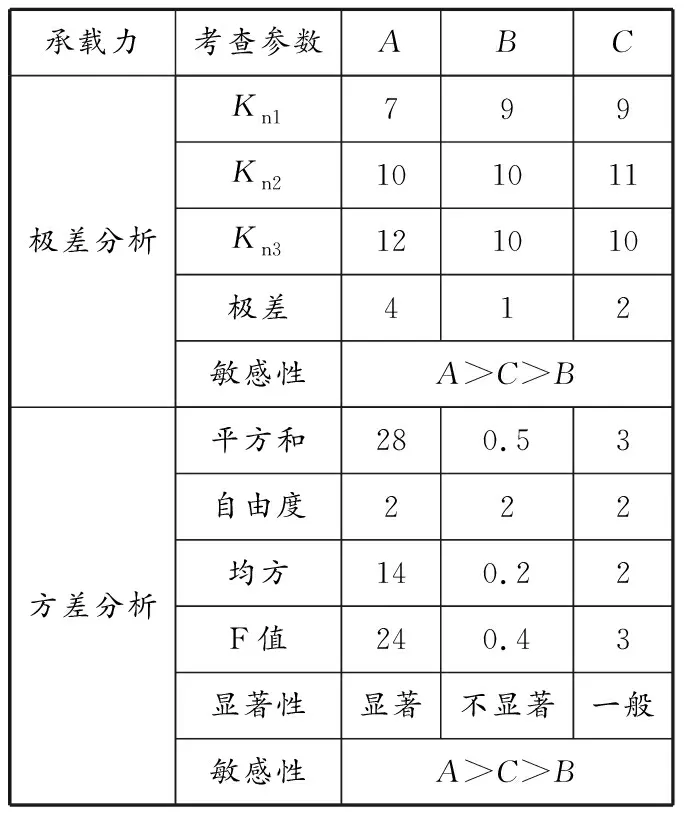
表 6 连梁构件变形能力分析结果
在不同影响因素下9个RPC连梁构件极限位移见图25。跨高比越大,构件极限位移越大,变形能力越强;箍筋量的变化对构件的变形几乎无影响;保持其他2个因素不变时,选择对角斜筋的配筋方式,构件的极限位移最大。
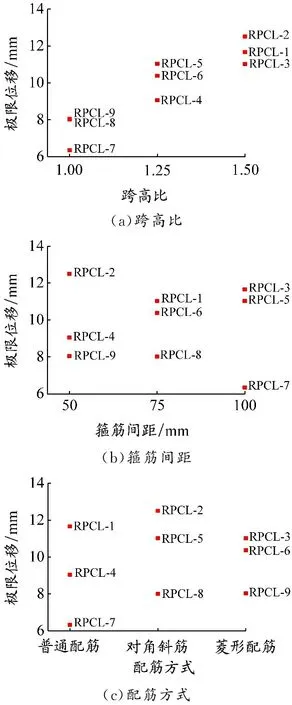
图 25 不同影响因素下连梁构件的极限位移
3.2.5 耗能能力
计算得到各因素对RPC连梁最大耗能量的影响,结果见表7。当承载能力、变形能力相同时,跨高比对构件影响最大,配箍量影响最小。
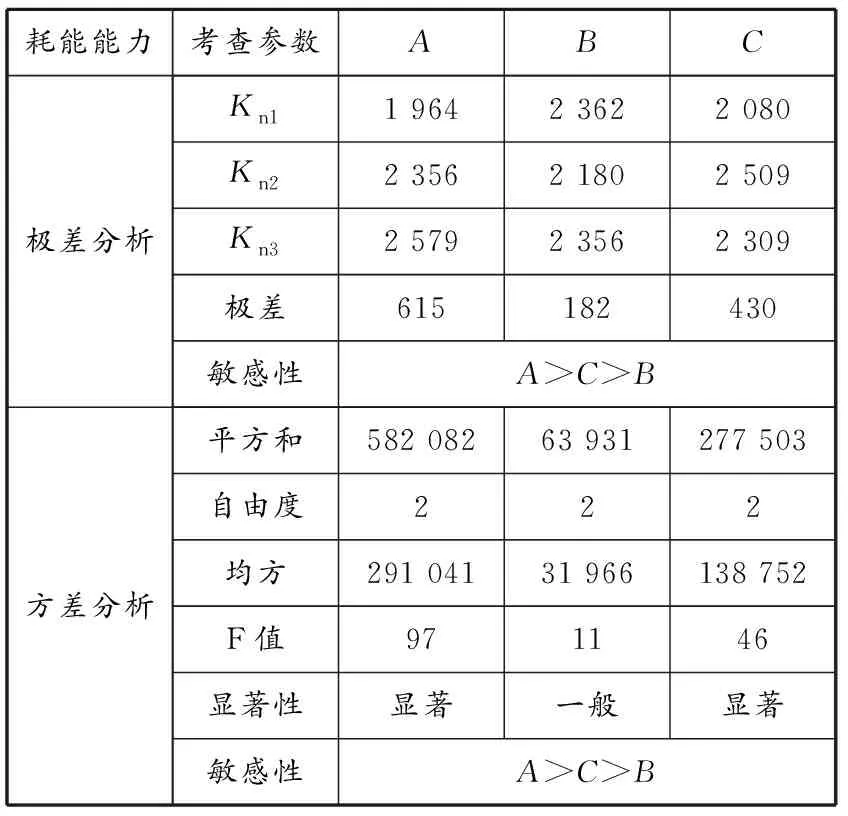
表 7 连梁构件最大耗能量分析结果
将3个因素对应的最大耗能量见图26。随跨高比增大,RPC连梁构件的最大耗能量相应提高;箍筋间距与最大耗能量间无明显规律;选择对角斜筋的配筋方式,构件最大耗能量相对较高。
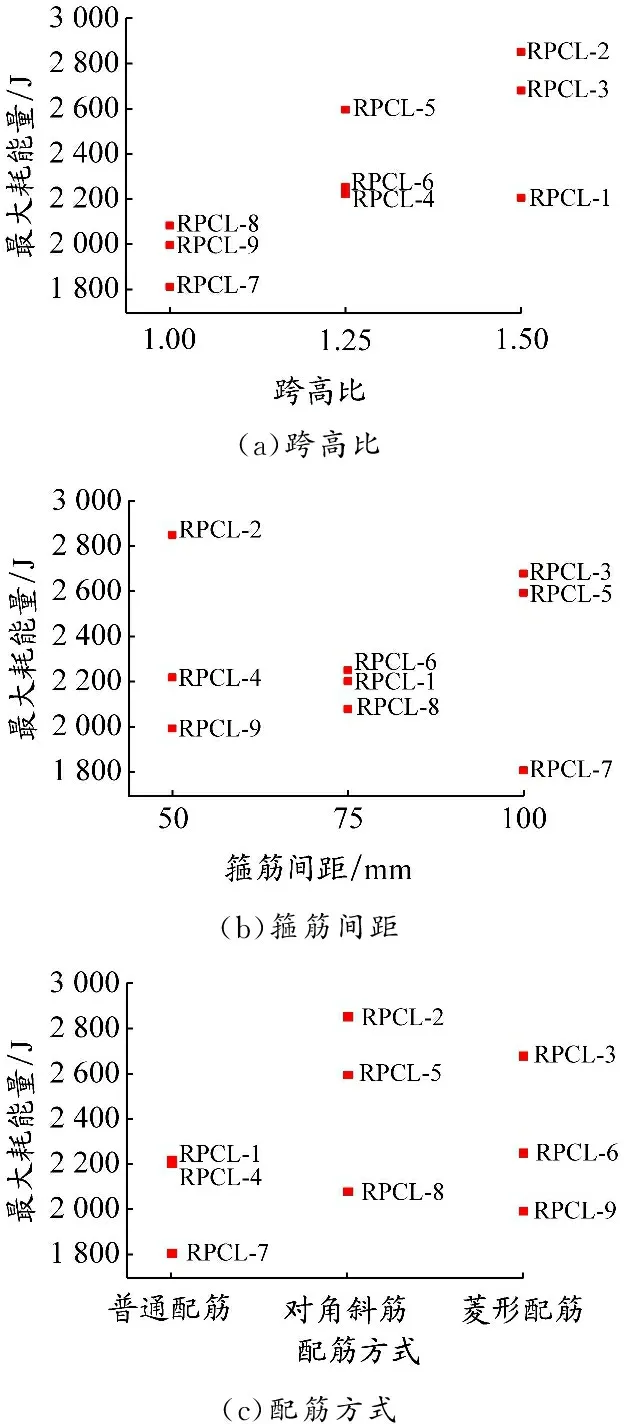
图 26 不同影响因素下的连梁构件最大耗能量
4 结 论
利用Abaqus软件对RPC连梁的抗震性能进行有限元数值模拟,模拟滞回曲线与试验结果吻合,证明模型的本构关系合理。在此基础上,进行RPC连梁正交试验模拟,分析跨高比、箍筋量和配筋方式对构件承载能力、变形能力和刚度等性能的影响。主要结论如下:
(1)RPC连梁构件的位移加载过程可分为2个阶段,一是加载初期弯曲变形阶段,二是构件的活性粉末混凝土受拉开裂后的剪切变形阶段,此时RPC连梁破坏形态为弯剪破坏。
(2)根据正交试验分析可知,跨高比对RPC连梁抗震性能影响最大,随着跨高比增大,构件的变形能力、耗能能力均出现不同程度改善,同时刚度退化速度减缓。箍筋量对抗震性能影响不明显。菱形、对角斜筋配筋方式的抗震性能均好于普通配筋方式;采用对角斜筋时,横向钢筋可以协同变形。
(3)对比RPC连梁抗震性能影响因素,建议小跨高比RPC连梁设计时应选择跨高比不小于1.25、对角斜筋的配筋方式,同时为保证充分发挥箍筋作用,箍筋间距应不低于75 mm。
