正弦平滑时间幅度调制的低抖动时钟信号产生*

苏燕婷,宋茂忠,崔 畅,沈 通,严 峰

(南京航空航天大学 电子信息工程学院，南京 211106)

0 引 言

低抖动时钟[1]广泛应用于光通信、卫星导航、模数转换(Analog-to-Digital Conversion，ADC)等领域，是高精度的信号模拟和信号采集的关键技术。在卫星信号模拟方面，毫米级高精度伪距时延[2]成为了模拟器的核心指标。多数研究聚焦于分数时延滤波或数值插值方法，但时延滤波等方法的参数相对固定，难以达到快速转换的目的。另一种满足快速可调要求且复杂度低的高精度时延实现方法是数控振荡器(Numerically Controlled Oscillator,NCO)。NCO通过控制码频率与码相位来实现伪距时钟的可控变化，文献[3]就采用了NCO方法来快速完成卫星动态信号的调制。普通的NCO受限于激励时钟的频率而导致产生的伪距时钟信号有一定的过零点抖动误差，不能满足高精度需求。文献[4]提出在NCO的基础上采用时间幅度调制时钟方法，消除了NCO时钟的过零点抖动误差问题，但经过数模转换后的带限通道会引入滤波失真。

本文针对时间幅度调制方法的滤波失真问题提出一种正弦平滑改进的时间幅度调制方法。本文介绍了时间幅度调制原理，分析了时间幅度调制时钟的带限失真问题，并采用正弦平滑方式对失真进行了有效抑制。对低抖动时间幅度调制时钟信号进行了Matlab仿真，并利用现场可编程门阵列(Field Programmable Gate Array,FPGA)硬件设计和产生，分析改进后时钟信号的精度变化。

1 时间幅度调制原理

NCO由N位相位累加器和N位寄存器组成，通过对频率控制字进行累加来产生所需频率的信号。在利用NCO产生时钟信号时，对N位相位的寄存器只截取其最高位，最高位有效时则时钟有效。在实际应用中，若采用250 MHz采样时钟fs产生1.023 MHz且随多普勒频移[5]变化的测距码时钟fcode，其理想的时钟上升沿如图1中实线所示。

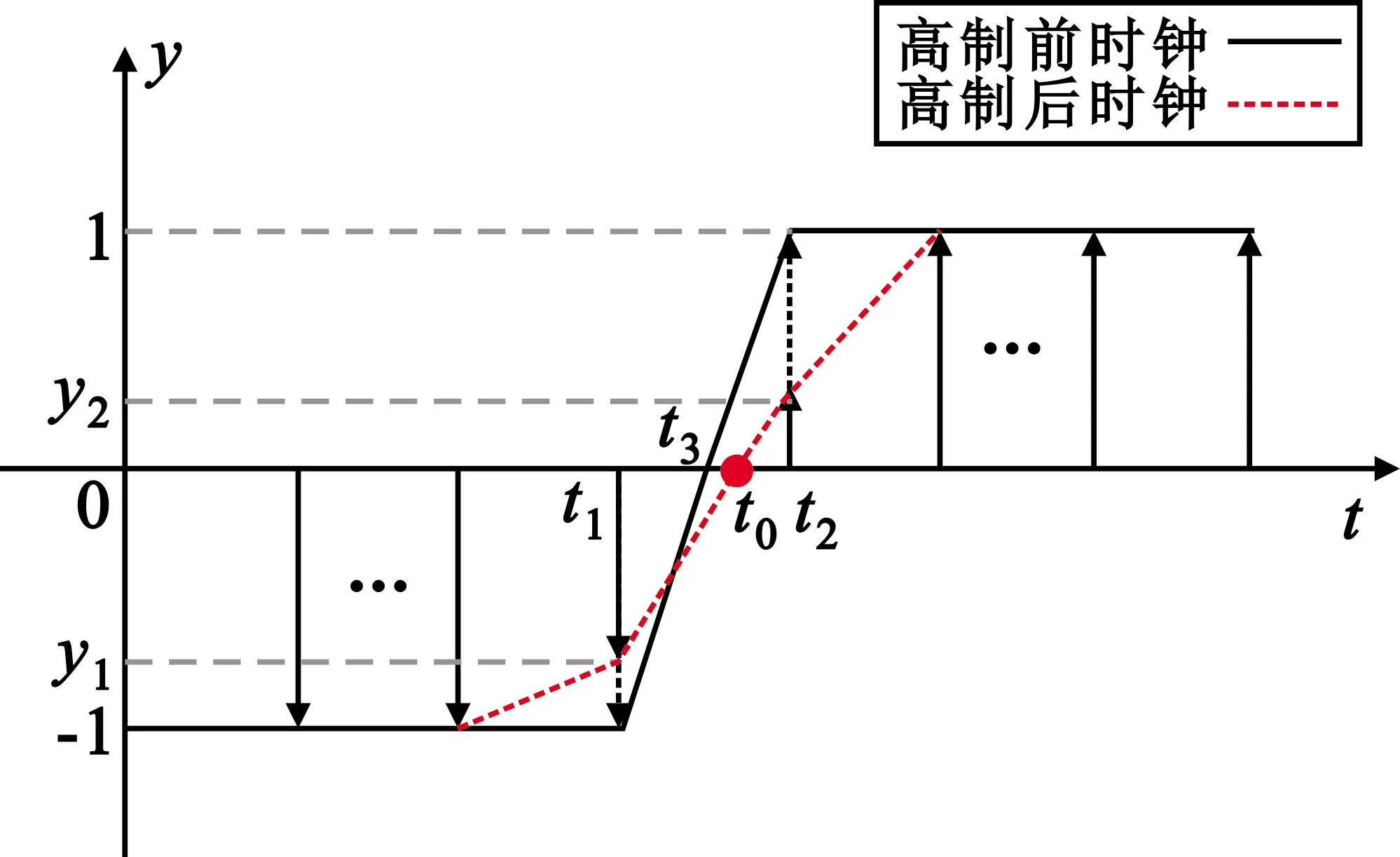
图1 时间幅度调制前后时钟过零点对比图

待产生的时钟周期Tcode与采样时钟周期Ts的比值如式(1)所示，其中N表示相位位宽，K表示频率控制字，m表示非负整数，d表示小数。

(1)

由公式(1)计算可得Tcode与Ts并非整数倍关系，即d≠0。由图1可以看出，在d≠0的情况下，过零点t0不能被直接采样，而只能得到其前后两个采样点t1和t2。由于NCO时钟对相位进行了1 b截取，采样点的幅值分别为-1和1，这样产生的时钟过零点将是这两个采样点的中点t3。实际过零点t3和理想过零点t0间的差值随时钟周期迭代不断变化，导致实际产生的时钟出现前沿抖动。

时间幅度调制能够应对NCO时钟的过零点抖动问题，其基本思想是用等间隔采样序列的幅度来表示信号的精确过零点时间，即将过零点到采样点的时间间隔调制到信号的幅度上。如图1中虚线所示，为了精确表示过零点t0的位置，根据采样点t1、t2与t0间的时间间隔，将采样点的幅值调制为y1、y2，在理论上修正了过零点误差。

经时间幅度调制后的采样幅值y1和y2表示为

(2)

式中：Ts=t2-t1表示相邻两个采样时刻的时间间隔，a=t0-t1表示上升沿过零点时刻与前一采样时刻的时间间隔，下降沿的采样幅值相反。时间间隔a与时钟周期有关，每增加一个周期，a将对应累加dTs。第i个周期的时间间隔ai表示为

(3)

分析周期内的采样点数，当第i+1个周期上升沿过零点的时间间隔ai+1超过一个采样间隔Ts时，Ts将对其取余，相应地第i个周期将增加一个采样点，因此第i个周期的采样点数Mi表示为

(4)

一个完整的时钟周期如图2所示，第i个时钟周期从当前上升沿过零点开始，至下个周期上升沿过零点结束。

图2 时间幅度调制时钟的第i个周期

(5)

(6)

2 正弦平滑抑制带限失真

经过时间幅度调制方法产生的测距码时钟由单比特信号变为多比特信号，测距码经过DAC后就可以与中频载波进行模拟调制，并射频产生卫星信号。但在实际应用中，由于DAC附带有滤除杂散分量的低通滤波器，斜率过高的上升沿经过带限通道将引起高频失真现象，导致过零点前后采样幅值发生变化，过零点时刻偏移。

如图3所示，利用Matlab对时间幅度调制时钟信号经过250阶的50 MHz低通滤波器进行仿真，时间上延迟了500 ns。将滤波前后信号进行对齐比较，经过低通滤波后，过零点前后采样点幅值分别由-0.758 6 V和0.241 4 V变为-0.453 5 V和0.271 1 V，出现了明显的高频失真现象[6]。

图3 滤波前后的时间幅度调制时钟信号

为了抑制上述带限失真问题，本文提出一种正弦平滑的方式对时间幅度调制时钟进行改进，即利用正弦函数对时钟边沿的采样点进行采样幅度调制，起到降低上升沿处斜率的作用。

正弦平滑改进后的时间幅度调制采样幅值与采样时间的关系如下:

y=sin(2πf(t-t0)) 。

(7)

式中：t-t0表示采样时间与时钟过零点时刻间的间隔，f表示正弦函数的频率。考虑到f需要小于50 MHz以满足滤波器截止频率，取250 MHz/12≈20.83 MHz，一个时钟边沿有6个采样点需要调整幅值。改进前后的时钟边沿如图4所示。

图4 改进前后时钟上升沿对比图

第i个周期上升沿的采样幅值表示为

(8)

式中：n=1,2,3,4,5,6分别表示图4中从左至右的6个采样点。下降沿各采样点幅值与上升沿相反。

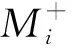
(9)

(10)

图5是正弦平滑前后的时钟信号的归一化对数振幅频谱，经分析，频谱峰值都在1.023 MHz频率处。由于对时钟边沿进行了正弦平滑，频谱泄漏造成的多余频率分量减少，正弦频率与采样频率的倍数关系减小了奇次谐波的影响。同时，正弦平滑后信号在50 MHz以上的频谱峰量明显减小，表明带限失真问题能够有效地被抑制。

图5 改进前后的时钟信号频谱图

经过正弦平滑后时间幅度调制时钟信号其滤波前后信号如图6所示。选取与图3相同的上升沿，滤波后，采样点幅值由-0.386 8 V和0.126 1 V变为-0.329 6 V和0.189 7 V，相较于改进前，幅值变化得到了控制，该周期的抖动误差也减小了35.2 ps。

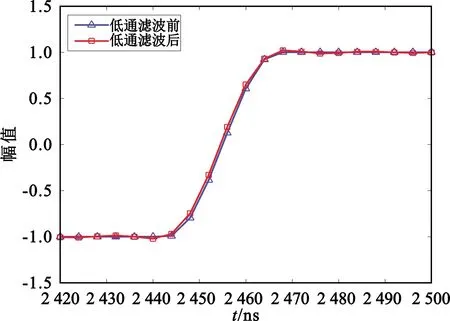
图6 改进后滤波前后的时钟信号

为统计周期标准差，对正弦平滑改进前后的时间幅度调制时钟在滤波后的周期抖动误差进行1 000个周期对比，理想的C/A测距码时钟频率fcode为1.023 MHz，周期Tcode为977.517 ns，图7给出了其中50个时钟周期的值。

图7 改进前后的时钟周期抖动对比

可以看出，经过正弦平滑改进的时钟周期抖动明显小于改进前，最高减小了82.5 ps的周期抖动误差。比较1 000个滤波后时钟周期的标准差，原时间幅度调制时钟和正弦平滑的时间幅度调制时钟周期标准差分别为83.7 ps和25.6 ps，改进后的周期标准差降低了69.42%，说明正弦平滑后的时间幅度调制方法能够极好地作用于低抖动时钟的产生。

3 低抖动时钟的硬件设计

本文还对低抖动时间幅度调制时钟进行了硬件设计，将时钟的产生分为周期内计数、过零点间隔累加和时钟幅值选择三个模块。计数器的模值M由累加器的溢出值Sig控制，经二选一MUX判断模值，计数器每完成一周期计数则累加器进行一次累加D。将累加后的值A送入幅值计算器计算幅值Y，最后14∶1选择器通过计数值Cnt选择输出时钟信号，具体如图8所示。在参数选择上，m为公式(1)中的整数分量，m0为初始码相位的整数分量，D和A为公式(1)和(3)中小数分量d和时间间隔a的48 b量化值，D0为初始码相位小数分量d0的48 b量化值。

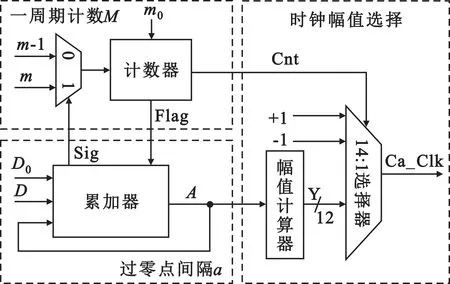
图8 低抖动时钟的硬件设计

幅值计算器同样需要一些设计。普通的NCO从ROM存储器中查表获得正弦幅值，有容量限制。为了能够根据公式(8)得到更为精确的量化幅值Y，本文采用CORDIC算法来计算幅值。在圆坐标系中，三角函数的正余弦值可以表示为向量形式，将初始向量r(xi,yi)经过旋转角度θ则得到目标向量g(xi+1,yi+1)。CORDIC算法经过n次固定角度θi的偏摆来逼近旋转角度θ，通过坐标旋转的方法来简化复杂的运算过程。

CORDIC算法方程组可以表示为

(11)

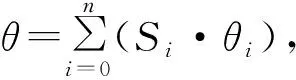
4 实验与分析

参照硬件设计，用正弦平滑的方式在FPGA端对低抖动时间幅度调制时钟进行时钟信号的产生。

首先，利用Mentor公司的FPGA仿真软件Modelsim进行仿真测试，设置激励时钟为250 MHz，对不同频率的时钟信号进行产生与分析，选取时钟信号的10个连续周期，经过计算，正弦平滑后的周期均值与周期标准差如表1所示，10 ps级的周期标准差与Matlab仿真结果相近。

表1 FPGA仿真不同频率时钟信号的精度

接着，载入Xilinx Virtex6系列FPGA开发板进行硬件测试，采用示波器对时钟信号进行可视精度对比，将两个时钟经过DAC及低通滤波后接入示波器的两个通道并观察频率和周期参数。由于示波器的频率显示精度为1 kHz，因此选择产生频率为1.022 MHz、1.023 MHz、1.024 MHz的时钟信号，以便获得直观的误差对比结果。读取两个通道的测量参数可得如表2所示的周期精度对比数据，其中通道1代表普通NCO时钟，通道2代表正弦平滑的时间幅度调制时钟。

表2 NCO与正弦平滑时间幅度调制时钟周期精度对比

考虑器件温漂、模数转换的相位截断、信号传输中的噪声、示波器精度等影响，周期标准差理论值为0的10 MHz基准方波在示波器中也有30 ps左右的标准差，因此，虽然表2中FPGA板级的时钟周期的标准差比仿真结果有一定的增加，但仍可以看出在不同频率下，正弦平滑的时间幅度调制时钟相较于NCO时钟的周期标准差降低了90%以上，证明产生的时间幅度调制时钟有远高于NCO时钟的稳定性。

图9为1.024 MHz频率时钟示波器画面，正弦平滑的时间幅度调制时钟的周期标准差为88.86 ps。

图9 NCO时钟与正弦平滑的时间幅度调制时钟精度对比图

5 结 论

本文提出了一种用正弦平滑改进的时间幅度调制方法，极大减小了NCO时钟的过零点采样误差，有效抑制了时间幅度调制时钟的带限失真问题。以卫星导航模拟器中的测距码时钟为参考时钟信号，通过软件仿真与硬件实现，对不同频率的时钟信号进行分析，证明正弦平滑时间幅度调制时钟的精度相较于普通NCO时钟提升了一个数量级，产生了高精度、低抖动的时间幅度调制时钟，在继承NCO时钟频率快速、可调优点的基础上，可观地减小周期抖动，能够应用于产生与采样时钟非整数频率关系的低抖动时钟信号，降低了低抖动时钟信号对高频率采样时钟的需求。算法易于实现且有较强的工程适用性。