一种间隔重访的低轨星座设计方法*
2022-06-28周李春
周李春
(中国西南电子技术研究所,成都 610036)
0 引 言
近年来,卫星广泛应用于网络通信、导航定位、对地遥感、气象监测和军事目标侦察等领域。卫星轨道和星座的设计,主要是根据其用途来确定。
在中低轨道上的全球连续覆盖星座主要应用于通信、导航领域,所需的卫星数量多、规模大。文献[1]提出的极轨“覆盖带”(Street of Coverage,SOC)星座设计方法,有效地解决了连续单重全球覆盖的卫星星座设计问题。文献[2]将极轨道 SOC 方法应用到近极轨道,如铱星(Iridium)星座采用了近极轨道 SOC 星座。Walker 星座[3]应用于倾斜轨道,星座的冗余覆盖比例相对较少,在多重连续全球覆盖星座设计中具有突出的优势,GPS、GALILEO、GLONASS 和 Global Star等很多中低轨卫星通信系统都采用了Walker星座。遗传算法近年来被引入星座设计领域:文献[4-6]采用了遗传算法对区域性覆盖的卫星星座进行设计优化,设计了针对指定区域的低轨卫星移动通信系统星座;文献[7-8]提出了改进的遗传算法,通过优化区域覆盖星座模型,降低算法复杂度。遗传算法适合星座设计参数多、条件限制复杂、没有解析式求导的工程应用问题,但选择不同的目标函数进行优化,获得的结果不同,计算时间较长。文献[9]提出了一种圆轨道和椭圆轨道的混合轨道卫星星座,可满足我国境内的通信要求。
上述全球覆盖和区域覆盖星座设计方法主要解决对地连续覆盖问题,但对于非连续覆盖的星座设计研究较少。在电子侦察、遥感等领域,由于地面目标固定,车船等目标的移动速度慢,即使间隔一定的重访时间,也能对目标进行跟踪监视,不需要连续覆盖。这样的星座既可满足应用需求,也能有效减少卫星数量,节约成本。
基于这样的背景,一个非连续覆盖的星座优化设计问题提了出来,即在满足一定重访间隔时间条件下如何设计卫星数量最少的星座。本文基于极轨覆盖带设计思路,通过改进全球连续覆盖的设计方法,将其应用到间隔重访星座设计中,得到不同轨道高度时的近似最优星座参数设计结果,并在STK软件中仿真验证了设计结果的正确性。
1 设计方法
星座设计过程中,卫星总个数、星座类型、最小地面仰角、轨道高度、轨道面个数等几个因素相互制约,影响设计结果。为简化问题,下面假设不同轨道高度时地面目标的最小仰角不变,以设计卫星数量最少的星座为目标。
1.1 极轨覆盖带星座设计方法
如图1所示,极轨覆盖带圆极轨道卫星星座的设计方法是先考虑同一轨道面内卫星的连续覆盖,卫星半波束宽度对应的地心角为α,同一轨道面内的卫星数量为Q,则相邻卫星间的地心角为2π/Q;然后考虑轨道平面间的连续覆盖,若相邻轨道面之间不考虑卫星相位关系,则覆盖的条带宽度对应的地心角为2ψ。
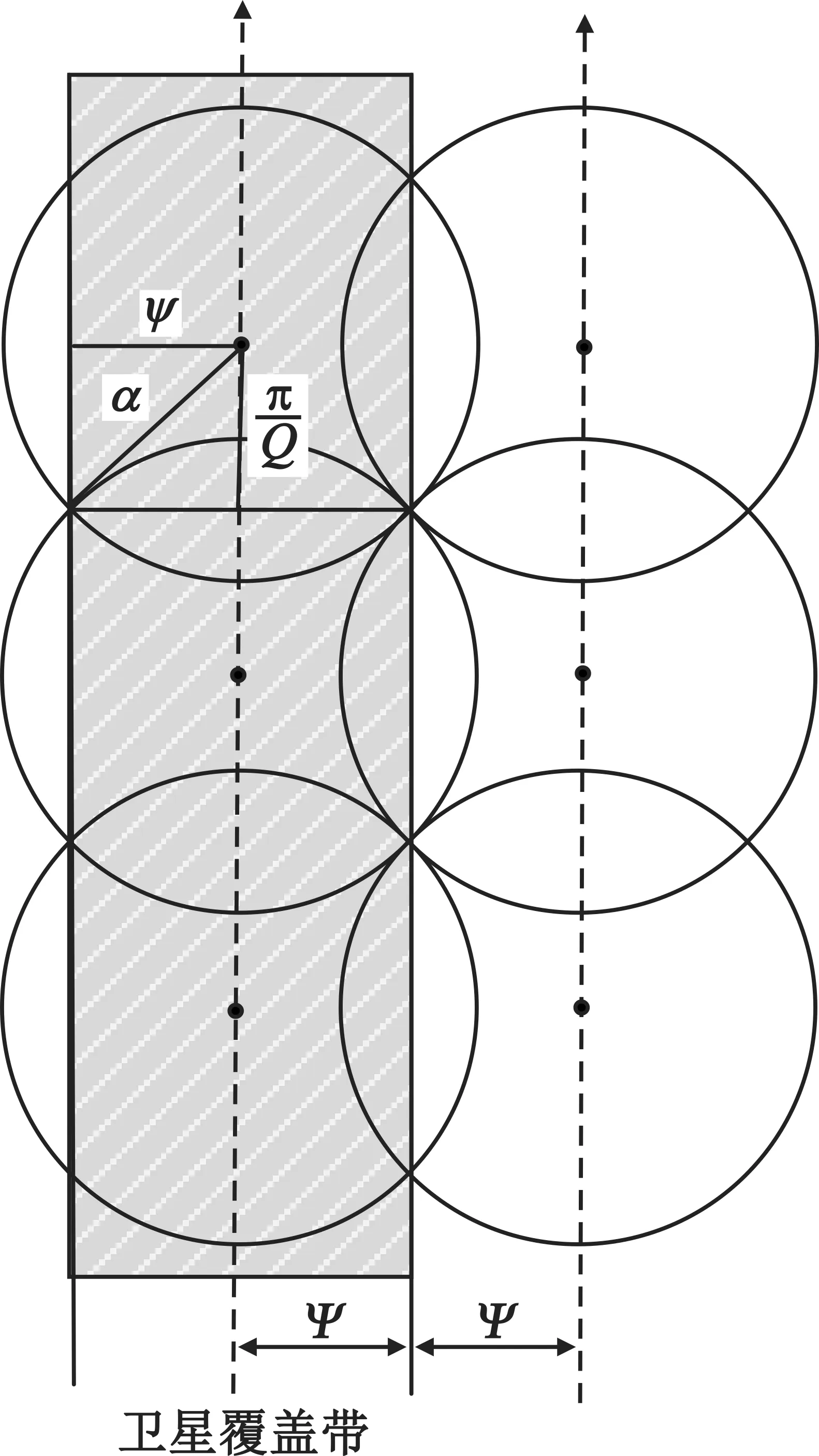
图1 卫星连续覆盖带
若地面目标的最小仰角为E,卫星轨道高度为H,目标所在位置的纬度为φ,那么对位于该纬度圈的目标连续覆盖的星座计算公式为[10]
(1)
式中:δ是覆盖带半宽度ψ在纬度为φ的纬度圈上对应的圆心角,P为轨道面的个数,N为卫星星座的总数。已知最小仰角和目标所在纬度时,通过上式计算可得到不同轨道高度时满足连续覆盖条件的卫星数量。
1.2 间隔重访星座设计方法
连续覆盖的相邻卫星波束间必须要交叠,而在间隔重访的条件下,卫星的数量减少,相邻卫星间的波束间存在覆盖间隙。由于圆形波束的中心和边缘对目标的覆盖时间长短不同,相邻波束的间隔时间也不同,为了简化设计,将其对地投影的圆形近似等效为正方形,如图2所示。

图2 等效覆盖区域示意图
将对地覆盖的圆形和正方形视为平面图形,面积分别为S1和S2,关系式如下:
(2)
式中:R为地球半径,α为半波束宽度对应的地心角,ψ1为正方形半边长对应的地心角。令两者面积相等,通过计算可得到α与ψ1的关系式。
若卫星轨道高度800 km,则运行一圈的周期为100.723 2 min;若覆盖范围最小仰角为10°,则α为18.96°,地面目标过星下点时,卫星波束的覆盖时间最长,为10.6 min;等效为正方形后,角度ψ1为16.8°,平均覆盖时间为9.4 min。
设重访间隔时间为ΔT,轨道周期为T,则重访间隔对应的地心角Δψ为
(3)
轨道间的重访间隔与地球自转相关,地球自转的角速度为ωe=0.004 178 07 °/s,间隔时间内转过的角度为
Δω=ΔTωe。
(4)
设同轨卫星数量为Q,那么该轨道面所有卫星的覆盖地心角度为2ψ1Q,间隔的角度为(Q-1)Δψ;设卫星轨道面数量为P,则相邻轨道面间的地心角为Δω+2ψ1。因此,间隔覆盖条件下,卫星数量Q和轨道面数量P的计算公式为
(5)
根据以上公式,计算P、Q的值并取整,可得到对赤道上的目标重访间隔时间为ΔT的非连续星座。
若目标位于纬度为φ的纬度圈上,由于纬度的增加只影响轨道面数量P的值,则ψ1与Δω可换算为
(6)
将ψ1′与Δω′替换式(5)中第二行的ψ1与Δω,计算出P、Q的值,则可得到对纬度圈φ上的目标重访间隔时间为ΔT的非连续覆盖星座。
2 验证与分析
为验证上述方法的有效性,首先设定重访间隔时间、最小仰角、轨道高度、目标位置等参数,计算星座中P、Q的值,然后根据星座参数在STK中建立仿真场景,输出覆盖时间、重访间隔等数据,从而对算法进行验证。
2.1 算法实现
设卫星波束覆盖范围内地面目标最小仰角E=10°,卫星轨道高度H为500~1 500 km范围内的低轨道,地面目标位于纬度0°,设计重访间隔时间小于15 min的低轨星座。根据公式计算得到的理论结果如图1所示。

图3 轨道高度与卫星数量关系曲线
由于地面目标最小的仰角不变,轨道越高,则覆盖范围越大,卫星数量也越少,与图中变化趋势一致。由于卫星数量和轨道数量的实际值为正整数,通过四舍五入取整得到的P、Q值与对应轨道高度H的范围如表1所示。
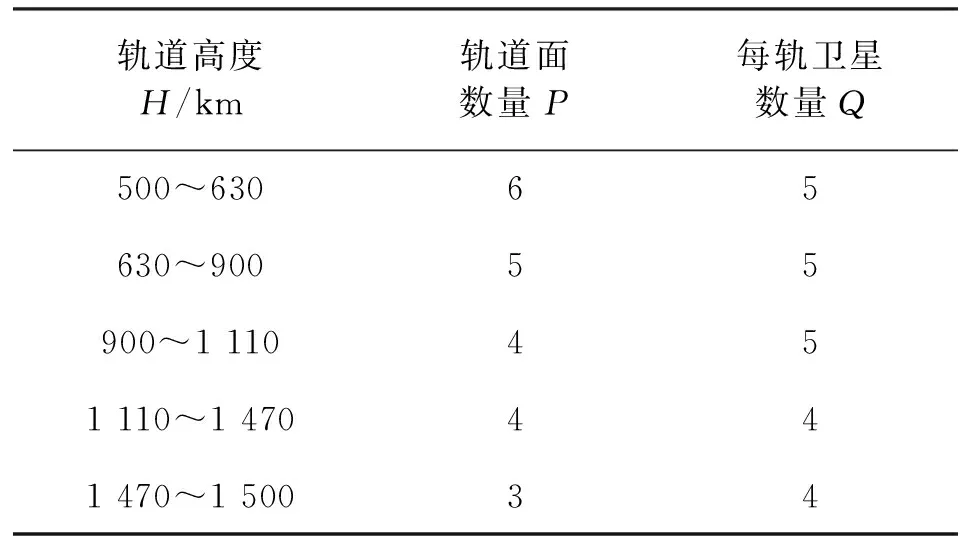
表1 不同轨道高度时P、Q的值(ΔT=15 min,E=10°)
2.2 仿真验证
在表1中选一组星座设计结果,在对应的轨道高度范围内取下限、中间值和上限三种情况进行验证。在仰角为10°时,分别将卫星轨道及波束参数设置到STK软件中,建立星座,设定地面目标在0°纬度上,仿真场景时间为1天。通过STK软件仿真,输出星座对目标的相关覆盖数据,然后统计星座对目标的重访间隔和覆盖性能,分别如图4和表2所示。

(a)H=630 km

(b)H=720 km

(c)H=810 km

(d)H=900 km
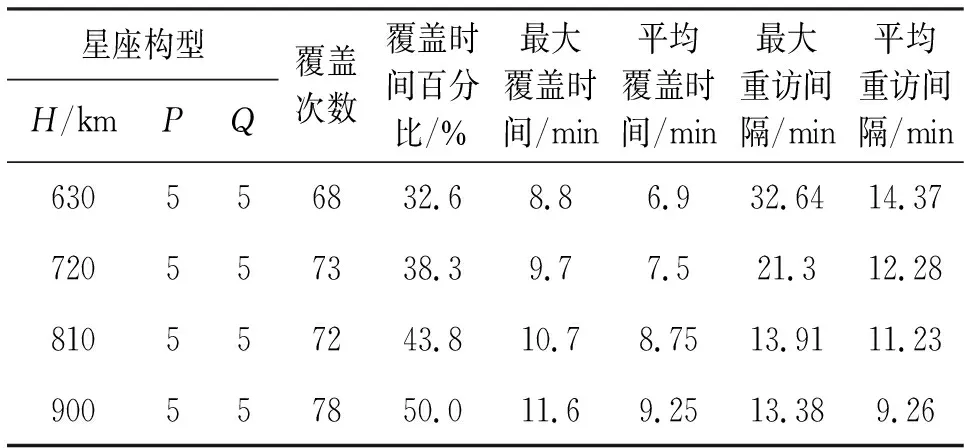
表2 星座覆盖性能统计表
从统计结果可看出,在星座构型相同时,轨道高度越高,星座对目标的覆盖时间越长,重访间隔越小,即覆盖性能越好。在H=630 km时,虽然最大重访间隔为32 min,但平均间隔为14.37 min,接近设定的15 min;随着高度增加,最大重访间隔和平均重访间隔都减小,在H=810 km时,最大重访间隔小于15 min。通过验证,卫星星座设计结果可满足平均重访间隔小于15 min的要求。
本文重点对目标位于0°纬度上的场景进行了设计验证。理论上,目标纬度越低,对星座的数量要求越多;反之,设计的星座若满足0°纬度目标的覆盖,则对其他纬度的目标覆盖也可满足。若目标位于其他纬度上,可采用相同的办法,通过式(6)计算得到满足条件的星座设计结果。
2.3 应用分析
通过分析与验证,采用本文方法设计间隔重访星座时,需注意以下几点:
(1)轨道面数量P和每轨数量Q的取值通过近似取整得到,星座设计结果为近似值而不是最优值;
(2)输入轨道高度范围较大时(如500~1 500 km),轨道高度越高,卫星数量越少,因此在距离、链路、运载能力等条件满足的条件下可选轨道高度尽量高,使卫星数量较少;
(3)在一定高度范围内(如630~900 km),设计的星座构型相同,但轨道高度越高,覆盖性能越好(见表2),可根据相关情况选择适合的轨道高度。
3 结束语
本文提出了一种实用的低轨星座设计方法,用于解决特定领域中非连续覆盖的星座优化设计问题。该方法基于极轨覆盖带的设计思路,通过近似等效的方法改进,可在设定对地面目标的平均重访间隔时间、波束宽度等参数时得到不同轨道高度时的近似最优星座参数。通过STK软件对设计的星座进行仿真验证,其结果可满足平均重访间隔时间要求。该方法适用于低轨电子侦察、遥感、对地观测等领域,对星座系统的总体规划设计具有一定的参考价值。该方法基于极轨道设计的卫星星座,也适用于近极轨道。
针对倾斜轨道的间隔重访星座优化设计方法,需开展进一步的研究工作。
