宽带多载波微波光链路多源非线性数字补偿方法*
2022-06-28宁婕妤
宁婕妤,王 群
(1.中国西南电子技术研究所,成都 610036;2.93128部队,北京 100843)
0 引 言
卫星通信具有覆盖范围广、作用距离远、可靠性高、组网灵活、不受地形限制等突出优点,为主干网和边缘节点提供了一条直达的捷径,将区域通信网络延伸至地球的每个角落,极大地弥补了地面通信网络覆盖不足的缺陷,成为信息系统实现全球通信服务的主要途径[1-3]。未来个人信息时代,若要实现“全球个人通信”,通过卫星通信系统与地面通信系统相融合将得到满足[4-5]。卫星移动通信作为主要的通信手段之一,正向“多波束、大容量、智能化”方向发展,而现阶段成熟的卫星通信主要是微波通信,其通信频段将很难满足未来高速率、大容量的通信需求,且难以实现小型化[6-7]。
微波光子技术为下一代卫星移动通信发展带来了新希望。该技术将微波与光子两大技术相融合,利用微波光子技术实现信息处理、控制和传输,秉承了光的高速、宽带、透明、低功耗及潜在的低成本等诸多优势,将大大提高微波特别是毫米波信号的处理能力,在未来宽带卫星通信发展中具有良好的应用潜力[8]。此外,随着人们对通信带宽需求激增,若面向30~70 GHz高频通信,该技术还可克服信号处理的电子采集瓶颈,并具备更为灵活强大的并行处理能力和高解析度。
虽然微波光子技术优势众多,但由于光纤链路及系统器件的非线性特性,特别是电光调制器的非线性特性,将会导致信号畸变。以最常见、使用最广泛的马赫-曾德尔调制器(Mach-Zehnder Modulator,MZM)为例,尽管铌酸锂材料本身非常稳定,具有低损耗、使用寿命长、受温度及系统波长影响小等特点,且可处理的信号带宽和光功率较高,但由于其传输函数的正余弦特性,当输入的射频信号功率较大时,输出信号将产生严重的失真,进而影响到整个系统的增益及动态范围等指标,因此,实现系统射频信号的无失真输出是当前光子辅助超宽带射频信号传输与处理所面临的重要挑战。对于宽带多载波微波模拟光链路系统而言,主要面临谐波失真、三阶交调及互调非线性失真等多种非线性失真问题。一般选取合适的滤波器可以消除谐波失真,但三阶交调及互调非线性失真则无法简单移除[9-11],因此,消除宽带微波光子系统的多源非线性失真是该技术未来应用所亟需解决的关键问题之一。
目前,多种线性化方法被提出,如预失真线性化技术[12]、基于前馈控制的线性化技术[13]、调制器级联技术[14]、基于数字信号处理(Digital Signal Processing,DSP)的失真后补偿线性化技术[15]、基于光边带抑制的线性化技术[16]、基于非线性失真抵消的线性化技术[17]、相位调制相干探测及同相/正交(In-phase/Quadrature,I/Q)解调技术[18]等,而这些技术较多地只针对某种特定类型的非线性失真。
综合比较可知,基于DSP的失真补偿技术相对来说应用较为灵活、成本较低,为宽带多载波系统的非线性失真抑制提供广阔的研究空间。在未来超宽带、多载波的环境中,不仅存在三阶交调非线性,不同的射频载波之间即使间隔很远,仍然会存在载波间的互调非线性,它们占据了更宽的带宽,这就意味着其失真的补偿和抑制需覆盖整个工作带宽。正由于互调非线性失真产生机理的特殊性导致传统窄带的失真抑制手段失效,而宽带多载波链路传递函数受整个工作带宽随机输入的多个载波影响,传统的DSP失真补偿方法在运用时需重新修改。
基于以上问题,本文提出了一种新的多源非线性数字补偿方法,仅需要获知系统的调制器工作点及输出截断点信息即可完成三阶交调、互调等多源非线性失真的共同补偿,避免了获知系统具体的特征参数所带来的额外复杂度,算法简单易于实现,保证了光载超宽带射频信号的线性传递。本文介绍了该方法的系统结构及原理,设计了相应的系统实验,验证了方法的有效性。
1 原理模型
本文所提出的宽带多载波微波光链路系统的线性化方法的实验结构图及数据处理单元的非线性失真补偿算法流程图分别如图1(a)和(b)所示。

图1 宽带多载波微波光链路线性化方法实验结构及算法流程图
由图1(a)可知,激光器发出的连续光经光放大器功率放大,被分光比为1∶1的光耦合器分成两路,上支路及下支路分别被铌酸锂MZM调制,调制器1加载宽带射频信号;调制器2加载本振信号,调制后上支路的信号光与下支路的本振光在光耦合器耦合之前分别经过光纤布拉格光栅和环形器的组合实现单边带滤波,得到单边带的信号光与单边带的本振光;最后,上、下支路的单边带的信号光与本振光拍频并由光电探测器检测得到中频输出信号,经过高精度的数据采集卡(Analog-to-Digital Conversion,ADC)采集,中频信号的模拟信息转化为数字信息,在数据处理单元完成非线性失真的算法补偿。
由图1(b)可知,非线性算法补偿将分两步:第一步,互调非线性失真补偿;第二步,三阶交调非线性失真补偿。当系统处于超宽带、多载波工作条件时,多载波链路虽然具有超宽带的工作特性,但具体到某个信道仍具有窄带特性,因而利用滤波手段提取窄带数字信息,结合系统的非线性传递函数特性,分析宽带系统多源非线性产生的物理机制并构建失真补偿模型,将是一种可行手段。下面将从理论上对本文算法进行详细说明。
一般来说,可由通用的泰勒级数展开模型表示系统的非线性传递函数。由于高阶谐波的幅度具有骤减特性,在小信号情况下对系统影响较小,因此,忽略三阶以上高阶谐波分量,系统传递函数表达式为
y=a0+a1x+a2x2+a3x3。
(1)
式中:系数ai(i=0,1,2,3),为链路的特征参量。宽带多载波射频信号包含多种频率成分,每种频率成分的中心角频率为ωk,幅度为Ak,因此,数学上表示为
(2)
将式(2)代入式(1)中,则有
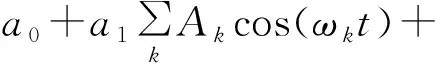
(3)
对于式(3)中的第一项及第二项,其展开形式分别为
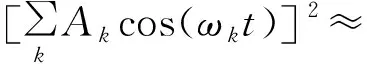
(4)

(5)
将式(4)及式(5)代入式(3)中,进一步整理得到输出失真信号为
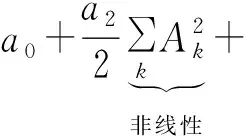
(6)
经过系统上支路单边带信号光与下支路单边带本振光拍频后得到中频信号。由式(6)可知,超宽带多载波工作状态下,频率为ωIF的中频信号不仅受到系统带外信号对带内信号的影响,即互调非线性失真,又受到系统带内交调非线性失真影响,主要为三阶交调非线性失真,两种非线性失真共存。如图1(b)所示,在数据处理单元,为了构建互调非线性失真补偿信号,分别利用低通滤波和带通滤波方式提取失真信号的基带项y0与基频项y1,分别如下:
(7)
(8)
根据式(7)与式(8),在小信号近似情况下完成如下算法处理:

Akcos(ωIFt)。
(9)
由式(9)可知,当γ=-3a3a0/a1a2时,系统载波间的互调非线性失真将得到抑制,补偿后的形式为
(10)
由式(10)可知,系统仍具有三阶交调非线性失真。利用基频项平方滤波的方式实现三阶交调非线性失真补偿,即
Akcos(ωIFt)≈
(11)
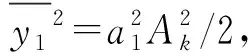
本文系统为工作点设置在低偏置工作状态的强度调制-直接检测系统,输入射频信号为两个双音信号所组成的四音信号,系统输出的失真信号在数据处理单元中完成第一步后,再次通过滤波手段分别提取出两个载波信号S1、S2,并基于上述补偿思路,分别构造三阶交调非线性失真补偿函数:
(12)
(13)
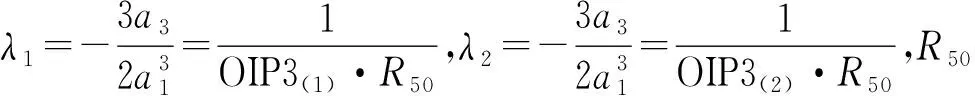
基于以上分析,利用如下算法消除系统的三阶交调非线性,最后,输出的线性化中频信号SL1和SL2分别表示为
(14)
(15)
由此可知,准确获知特征系数a0~a3是实现本文算法补偿的关键。对于低偏置强度调制-直接检测系统,传递函数还可表示为
(16)
式中:Vπ是半波电压,φ为调制器实际工作点相对正交偏置点的角度偏差值,R为探测器的响应度,IPD为探测光电流,ZPD为探测器的等效匹配阻抗。
将式(16)展开,忽略高阶项得到

(17)
将式(17)与式(1)对比可知,特征系数a0~a3具体表达式如下:
a0=RIPDZPD,
(18)
(19)
(20)
(21)
当系统处于低偏置时,θ=π/2-φ,根据以上特征参量,可确定补偿系数
(22)
由式(22)可知,补偿系数γ仅受调制器偏置点影响,与系统其他参数无关,而调制器的偏置点通过商用的偏置控制器可简单获得。综上可知,本文所提出的线性化方法,只需获知系统调制器的偏置点及系统输出截断点,无需利用硬件手段构建新的非线性失真补偿路径,即可实现多源非线性的算法补偿,保证了光载宽带射频信号的线性化传递。
2 实验分析
为了进一步验证本文所提的线性化算法的有效性,按照如图1所示的结构搭建实验平台,参数设置根据光电器件实际应用情况而定,输入系统的多载波射频信号为随机选取,但受实验条件ADC带宽限制,变频后的中频信号尽量保证在百兆以内。激光器输出的连续光载波波长为1 550 nm,功率为16 dBm,MZM电光调制器1与2的工作带宽为20 GHz,调制器1的偏置角度为120°,调制器2的偏置角度为正交偏置点,利用偏置控制器保持调制器偏置点稳定。调制器1加载的宽带射频信号为两个双音信号A与B组成的四音信号,双音信号A的频率分别为2.499 GHz和2.5 GHz,双音信号B的频率分别为14.997 GHz和15 GHz。调制器2加载的本振信号为频率分别为2.481 GHz和14.938 GHz组成的双音信号。经过光电探测器检测后,系统最终输出的中频信号被采集速率为200 Msample/s的数据采集卡数字化,并在图1(b)所示的数据处理单元利用离线的Matlab程序完成多源非线性失真补偿。
2.1 互调非线性失真补偿
当宽带多载波微波光链路系统中两个双音信号的射频功率分别为4.5 dBm和5 dBm、本振信号功率为13 dBm时,系统输出中频信号的频谱如图2(a)所示。由图2(a)可以看出,未经过任何算法补偿的信号失真非常明显,两个双音信号的基频分量对互调非线性失真分量的抑制量分别为27.31 dB和30.01 dB。按照图1(b)第一步完成互调非线性失真算法补偿后,信号频谱图如图2(b)所示,两个双音信号的基频分量对互调非线性失真分量的抑制量分别达到62.29 dB和57.89 dB。由此可见,系统的互调非线性失真分别改善了34.98 dB和27.88 dB。
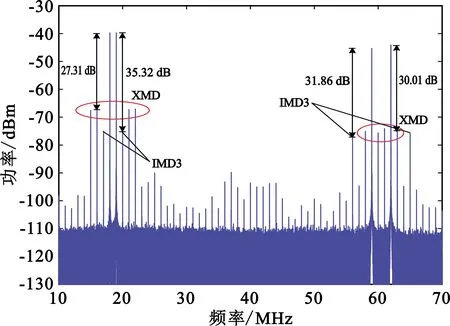
(a)未经任何DSP算法补偿的信号频谱图

(b)经互调失真算法补偿后的信号频谱图图2 宽带多载波微波光链路系统检测到的信号频谱图
2.2 三阶交调非线性失真补偿
通过带通滤波手段分别提出两个双音信号,标记为信号A与信号B,按照如图1(b)所示的算法流程单独对信号A与信号B进行三阶交调非线性失真补偿。由图2(a)可知,未进行算法补偿的信号A的基频分量对三阶交调非线性失真分量的抑制量为35.32 dB,信号B的基频分量对三阶交调非线性失真分量的抑制量为31.86 dB。经过三阶交调非线性算法补偿后,信号A与信号B的频谱如图3(a)与图3(b)所示,其基频分量对三阶交调非线性失真分量的抑制量分别为61.29 dB与58.01 dB。对比图3(a)与图2(a)可知,信号A的三阶交调非线性失真改善了25.97 dB。同理,对比图3(b)与图2(a)可知,信号B的三阶交调非线性失真改善了26.15 dB。

(b)信号B图3 经过三阶交调非线性失真算法进一步补偿的信号频谱图
2.3 无杂散动态范围
最后,分别扫描信号A与信号B的输入功率,记录信号基频对三阶交调非线性失真的抑制比,得到如图4(a)与图4(b)所示的无杂散动态范围图。可以看出,未经过系统线性化算法补偿,输出信号的非线性交调失真功率随着输入信号功率增大呈3倍速度增长;而经过系统线性化算法补偿后,呈5倍速度增长,表明系统输出信号的三阶交调非线性失真几乎完全得到消除。需要说明的是,图4(b)经过非线性算法补偿后,数值拟合稍有偏差是由于系统经过非线性失真抑制,信号高阶功率较低,容易受噪底影响而出现测量误差,属于较为正常现象。由图4(a)与图4(b)可知,信号A与信号B的无杂散动态范围分别提升了20 dB和18 dB,验证了线性化算法的有效性。
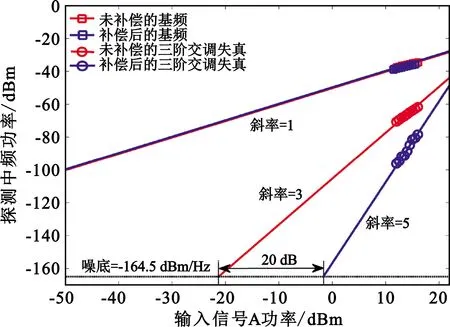
(a)扫描信号A输入功率

(b)扫描信号B输入功率图4 经过非线性失真算法补偿的系统无杂散动态范围图
3 对比及建议
目前,较为典型的多源非线性失真补偿技术主要有互调和交调失真后补偿技术[19]、基于预失真的互调失真补偿技术[20]、数字互调和交调失真补偿技术[21]等,本文所提出的补偿方法与典型关键技术的对比如表1所示。由表1可知,本文所提出的补偿方法较明显地实现了系统互调及三阶交调非线性失真的共同抑制,算法简单可行,但也存在多载波系统单路载波信号跨频段应用受限问题,后续可针对该问题进行算法优化。

表1 典型多源非线性失真补偿技术对比
未来,宽带多载波微波光子链路非线性失真补偿技术可用于宽带、多功能雷达、电子对抗、卫星通信等领域,为了完全满足各领域的应用需求,建议后续的微波光子技术在两个方向进行深入研究:第一,高效的电光调制——目前微波光子链路的损耗较大,主要制约因素是电光调制器,它的半波电压过高,导致任何信号处理或者系统级联等操作均会引入较大的噪声系统代价;第二,集成、高精度的光频谱处理手段——因为光频和射频具有4~5个数量级的差别,光载射频信号的相对带宽均极窄,对其进行精细(百兆以下)操作非常困难。后续随着光电子器件及光电处理手段的不断发展完善,有望进一步推进微波光子技术的实用化进程。
4 结 论
本文针对宽带多载波微波光链路系统多种非线性失真共存问题,提出了一种多源非线性失真数字补偿方法。通过提取系统的非线性失真补偿信息、获取系统调制器的工作点及输出截断点信息,可有效地实现系统输出信号的三阶交调及互调非线性失真的数字化补偿。通过搭建实验平台,实现了系统互调非线性失真抑制34.98 dB,三阶交调非线性失真抑制26.15 dB,系统无杂散动态范围改善了20 dB。该方法无需构建新的硬件失真补偿路径,更无需获知系统全部具体特征参数,算法简单可行,满足未来超宽带多载波射频光子系统的线性化需求。
