组合式陆空两栖机器人的运动规划与仿真

李凯林，韩宝玲，罗庆生，朱 琛

（1.北京理工大学机械与车辆学院，北京100081；2.北京理工大学机电学院，北京100081）

1 引言

为了在复杂地形下顺利遂行多种侦查作业，灵活对多变的环境条件，将飞行器和足式机器人的优势相结合的陆空两栖机器人应运而生，且已成为国内外学者研究的热点[1-2]。文献[3]研发的HyTAQ Robo（tHybrid Terrestrial and Aerial Quadrotor），将四旋翼和笼罩相结合，空中飞行采用四旋翼模式，地面运动则通过调整飞行器的姿态使笼罩滚动。文献[4]研发了一款海陆空全方位机器人，该机器人由四旋翼飞行器和两个滚动轮式保护架组成，四旋翼实现飞行功能，通过轮式保护架滚动实现行走。文献[5]研发了一款海陆空通用机器人MUWA，该机器人由四个变距螺旋桨和一个外围环组成。上述提及的这些机器人其飞行器与地面机器人是一体的，无法分离单独工作，而且地面机器人上没有速度和加速度传感器，无法精确控制移动，不能适应复杂的地面环境。设计了一款组合式的陆空两栖机器人，使其兼具飞行器的灵活性和四足步 行机器人地面适应能力，既能实现结构分离，又能组合作业。

对于组合式陆空两栖机器人而言，为增强对地面环境的适应性，四足步行机器人的运动规划是尤为重要的。目前常用的步态规划的方法有文献[6]采用复合摆线作为摆动相足底轨迹，使用这种足端轨迹可以使足端在落地时的冲击为零。文献[7]通过椭圆足底轨迹得到了机器人对角运动步态，满足实际样机行走需求。而采用贝塞尔曲线为足端轨迹，让机身进行匀速直线运动，使机器人实现walk步态。该方法在ADAMS仿真环境下获得了较好的运动效果，进而验证了规划的可行性。

2 陆空两栖机器人构型方案

2.1 结构特点

组合式构型方案是将四旋翼飞行器和四足步行机器人功能进行结合，使其兼具四旋翼飞行器的灵活性和四足步行机器人的超强地面适应能力。它们可以实现结构上的分离，分别执行陆空领域的侦察任务，同时四足步行机器人可以作为地面基站，四旋翼飞行器可以自由的起落在四足步行机器人躯体上进行组合作业，这既能准确控制四足步行机器人克服复杂多变的地面环境，又能同时进行陆空领域的侦查作业。三维模型，如图1所示。

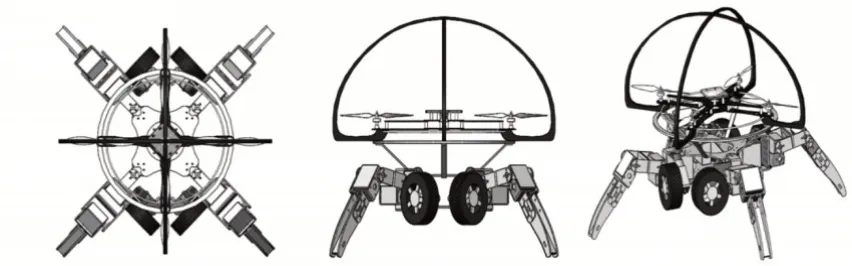
图1 组合式陆空两栖机器人三维模型Fig.1 A Three-Dimensional Model of a Combined Land and Air Amphibious Robot

四旋翼飞行器为标准的四旋翼无人机，机架为X构型的形式，考虑到四足步行机器人行走的速度问题，腿部采用轮腿复合式的结构，四条腿各配置一个自由度轮子，轮子分布在机器人的头部和尾部，以保证机器人的足够的足部运动空间。机器人的结构设计上依然沿袭了轻量化设计的理念，主体采用结构件，腿部零件在保证强度的情况下采用镂空设计。

2.2 四足步行机器人的腿部构型

四足步行机器人腿部结构可以采用二自由度与三自由度两种方案。二自由度单腿三维图与结构简图，如图2所示。采用双摇杆机构，其中，ac段为机器人的小腿，杆cd和杆be共同构成了机器人的中间腿，大腿为三副杆def。d和f为主动关节，构成了该腿机构的两个自由度。

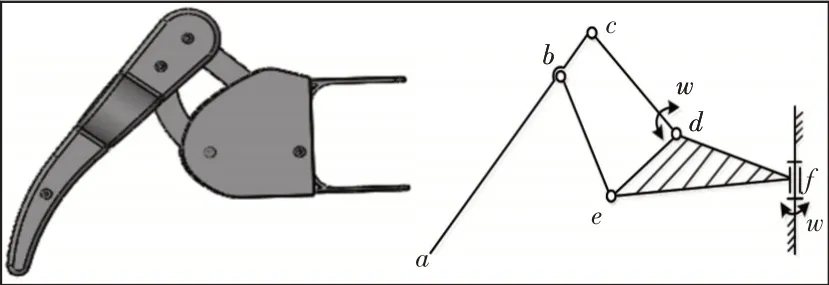
图2 二自由度腿构型Fig.2 Two Degrees of FreedomFreedom Single Configuration

两自由度腿机构可以实现机器人的大部分步态，但是两自由度的腿机构足端轨迹相对固定，足端的可达域太小。它的灵活性相对较差，难以适应比较复杂的地貌环境。四足步行机器人需要和空中机器人协同作战，以应对各种复杂环境，因此需要四足步行机器人工作空间大，运动灵活，显然二自由度构型无法满足要求。

采用三自由度腿部构型，机器人的髋关节，大腿关节和小腿关节各配置一个自由度，如图3所示。其中d关节固定于机器人的机体上，决定机器人的腿前进方向的摆动，而关节b，c决定机器人腿侧向的运动。三自由度腿机构相对于两自由度腿机构，具有更丰富的足端轨迹，使得通过调整腿部的位置来调节机器人的重心的方法有更多的选择，对于环境的适应能力更强。

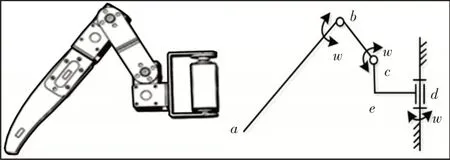
图3 三自由度单腿构型Fig.3 Three Degrees ofLeg Configuration

3 足式机器人的运动分析模型

机器人的正运动学是已知机器人的各关节的类型，相邻关节间的尺寸和相邻关节相对运动量的大小，确定机器人末端在固定坐标系中的位姿[8]。根据机器人的构型方案，采用D-H法对机器人整体整机模型进行了腿2坐标系的建立。机身坐标系{b}位于机器人的机体质心，y轴为前进方向，腿关节坐标{C}位于侧摆关节上，{W}为世界坐标系，如图4所示。根据D-H参数表得到足端相对于机身的变换矩阵，进一步得到足端轨迹点的坐标，这就是正运动学求解。而逆向运动学是已知机器人末端在固定坐标系中的位姿，来确定每一个关节的变化量[9]。这可以通过几何法或者在正运动学的基础上的解析方法来进行求解。

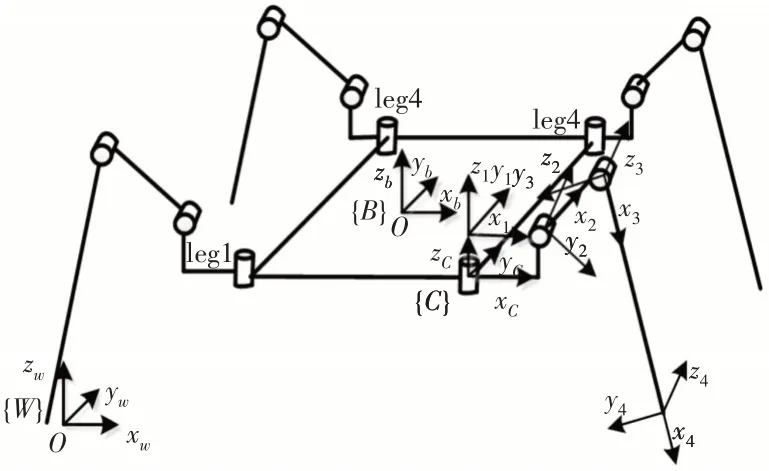
图4 机器人运动学模型Fig.4 Robot Kinematics Model

4 地面机器人的运动规划

4.1 步态规划分析

运动规划是保证机器人运动稳定性的关键技术，在机器人的研究中有着举足轻重的地位.考虑到四足步行机器人属于小型四足机器人，为了保证其运动的稳定性与流畅性，要求机器人可以在简单的地形下慢速稳定的行走。因此选用静步态，初步选定的步态为walk步态，所用的足端轨迹为贝塞尔曲线。

Walk步态规划中把机器人三条腿的支点形成的三角形叫做支撑三角形，使用中心投影法（COP）作为机器人的稳定性判据，即当机器人的重心在地面的投影点落在三角形内时，则机器人是稳定的，不会发生摔倒。把中心投影点到三角形边的距离的最小值叫做稳定裕度，稳定裕度越大，机器人越稳定[10]。当一个步序在运动中的任意时刻，机器人的稳定裕度都不为零时，认为该步序是稳定可行的。对于四足机器人而言，共有六种非奇异的静步态迈步顺序，在这六种迈步顺序中，1-4-2-3 为稳定裕度最优的[11]。因而，在机器人的迈步顺序中采用1-4-2-3的迈步顺序。如机器人步序图，如图5所示。

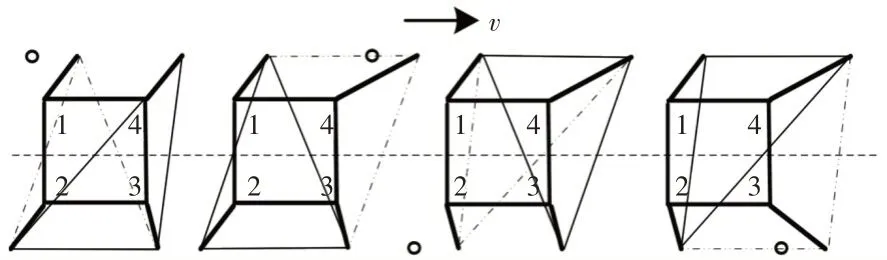
图5 机器人步序图Fig.5 A Sequence Diagram of a Robot

4.2 基于贝塞尔曲线的规划分析

贝塞尔曲线最初是按照已知曲线参数方程来确定四个点，然后首尾连接成多边形，接着通过贝塞尔公式逼近该多边形，从而得到贝塞尔曲线[12]。它的方程如式中（1）所示。实际的规划中采用插值法，即在贝塞尔曲线上选取一系列点，通过控制机器人的腿末端达到这些点即实现预期的规划。插值点的密集程度取决于规划的精度要求和机载计算机的性能[13]。

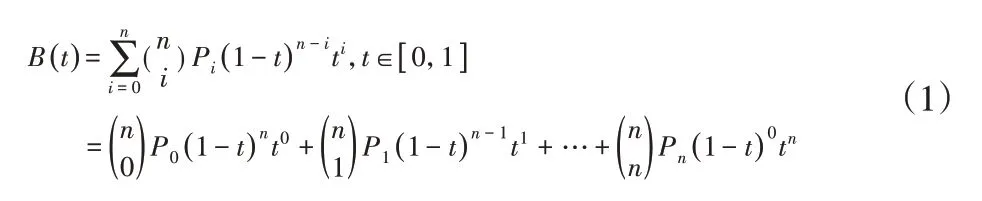
控制点两点重合，产生零速度；控制点三点重合，产生零加速度（即零受力）[14]是贝塞尔曲线衍生方程的特点，在X和Y方向分量上，坐标相同的控制点对该方向速度分量同样具有这样的控制效果。

在轨迹中加入换向点，使足端按轨迹曲线运动时，尽量减小对机体的冲击。从零点开始选用12个插值点坐标，如表1所示。它们可以满足四足步行机器人足端接地时Y方向的速度分量为0，足端加速度尽量平滑，保证抬腿高度。

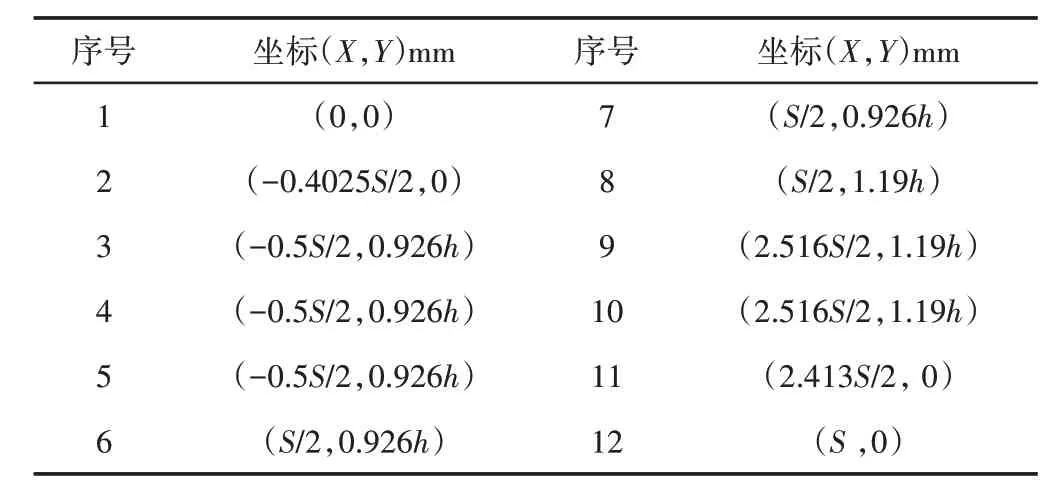
表1 贝塞尔曲线插值点Tab.1 Bayer Curve Interpolation Point

表格中S和h代表步长与步高，根据机器人设计方案，实际规划中步行速度v=0.05m/s，步高h=0.05m，周期T=0.4×4=1.6s，S=vT=0.08m。各条腿与第一条摆动腿的相位差［b1，b2，b3，b4］=［0.25，0.75，0，0.5］，负载因子β=0.78，机身长L为2m=116mm，宽W为2n=116mm。各腿节长度为L1，L2，L3，各关节初始角度为θ1，θ2，θ3，具体参数，如表2所示。因此得到各条腿的足端轨迹方程如式（3）～（7）所示，机身轨迹如式（8）所示，生成的贝塞尔曲线及各插值点，如图6所示。

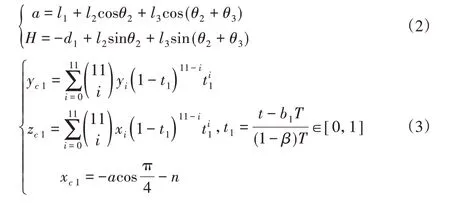
表2 步态参数Tab.2 Gait Parameter

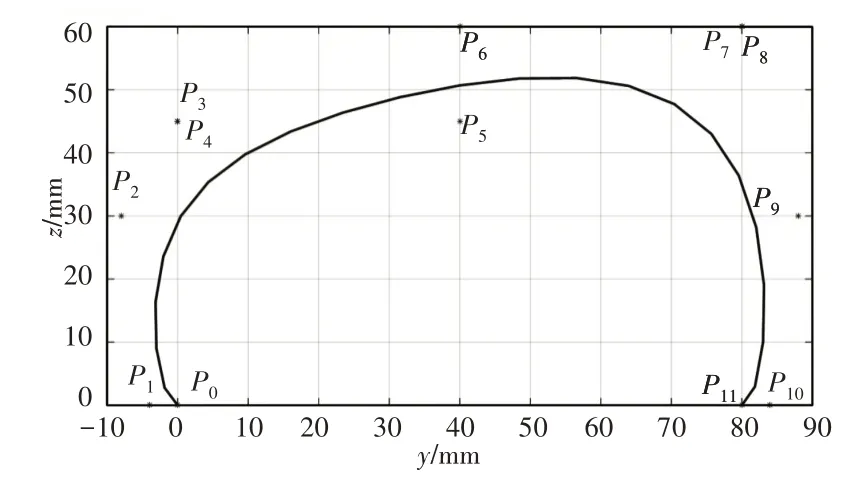
图6 足端轨迹图Fig.6 Foot Track Diagram

5 虚拟样机建模与仿真

虚拟样机技术是一种利用在计算机中建立的虚拟样机代替物理样机对产品进行设计测试和评估的方法，为了验证通过贝塞尔曲线规划得到的机器人步态的正确性，采用ADAMS 软件建立机器人虚拟样机模型，并进行仿真分析，所建立的模型，如图7所示。

图7 ADAMS模型Fig.7 ADAMS Model

通过仿真发现机器人可以稳定行走15个周期左右，其中前三个周期为准备阶段，从第四个周期开始进入正常行进阶段。通过分析仿真中机器人的机身位移和足端轨迹曲线，从而可以对机器人的稳定性和规划的有效性进行评估。

规划的机器人是匀速直线运动，因此最直接的观察方式是观察机身运动轨迹，机器人质心在X、Y、Z三个方向的位移，通过分析发现，机器人的位移曲线呈现锯齿状，这是因为在前进的过程中重心的变化产生了侧翻转矩，引起打滑现象导致曲线位移发生突变，如图8～图10所示。Y方向的位移曲线相对平滑，速度逐渐在加大，从4s之后，为一条斜率不变的斜线，对应的运动为匀速直线运动，且波动很小，说明机身沿直线前进。

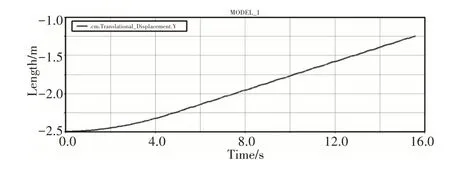
图8 机身质心Y方向的位移Fig.8 Displacement in the Y Direction of the Fuselage

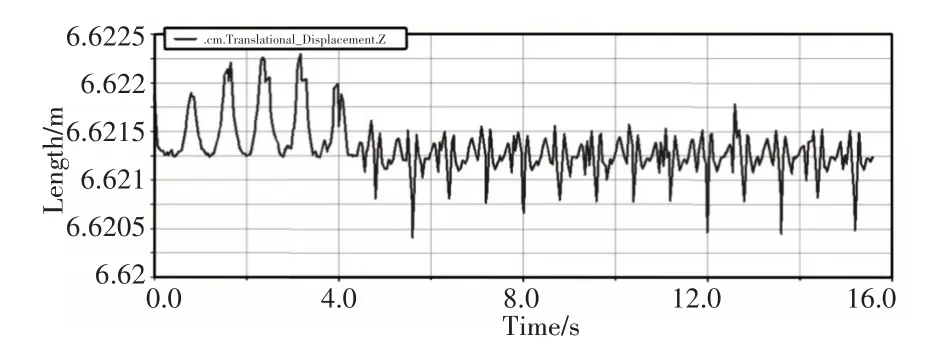
图10 机身质心Z方向的位移Fig.10 Displacement in the Z Direction of the Fuselage

X方向平均偏移量为2.5mm，对于行径的路程来说波动较小，说明机器人保持直线运动的稳定性较好。

Z方向的质心平衡位置偏移量约为0.5mm，主要是因为前三个周期是逐渐调整期，质心没有达到预定的位置，稳定后质心变化呈规律性且平衡位置固定，说明机器人稳定性较好。

机器人腿1的足端轨迹图，通过分析发现，足端位移在前进方向上和机身质心位移相似，不同之处是足端位移曲线有一些明显的尖点，这是前进过程中存在冲击的原因，如图11所示。在z方向上机器人最大位移和步高吻合，进一步说明规划是科学有效的。

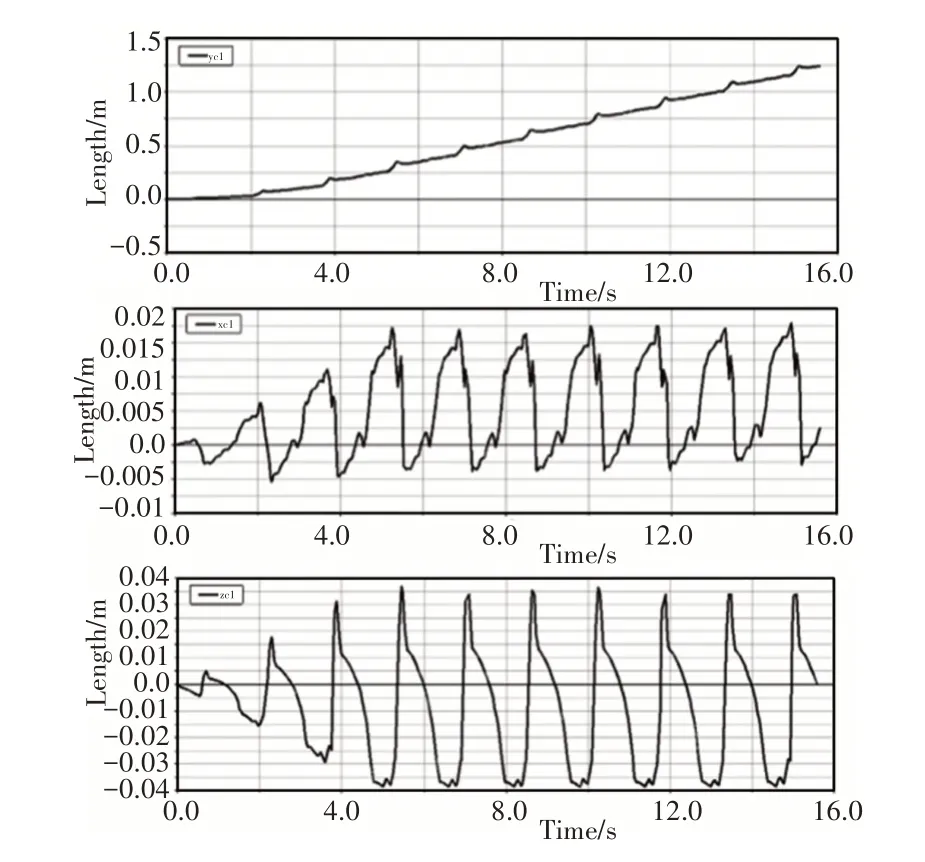
图11 足端轨迹图Fig.11 Foot Trajectory Map

6 总结

陆空两栖机器人结合了四旋翼飞行器与四足步行机器人的结构特点，为多用途侦查提供了更多的可能性。

（1）机器人可分离的结构设计不仅大大增强了陆空两栖机器人的环境适应能力，更为未来多样化的设计奠定了坚实基础。（2）足端轨迹采用贝塞尔曲线，规划机器人按直线运动，通过运动学求解得到各关节位移曲线，用MATLAB 求得位移点转化为驱动函数驱动虚拟样机机器人进行了15个周期的连续运动，且步行运动的流畅性、稳定性与灵活性，验证了该方法的正确性，并对物理样机的控制提供了理论指导，具有推广应用价值。