近距离煤层回采巷道支护方法研究

白邦旭

(山西省柳林县能源局，山西 吕梁 033300)

对于近距离煤层开采，在采动压力影响下，上覆煤层开采形成的采空区往往对其底板岩层构成造成不利影响，当两煤层距离较小时，导致底部煤层中的回采巷道在采动压力作用下发生变形甚至破坏，增加维护成本[1-3].为此，需要研究近距离煤层开采巷道稳定性问题，并提出有效的巷道支护方法。

曹海彬对于近距离煤层围岩支护，提出巷道采用锚网梁+架棚支护方案[4]；周波等指出在进行近距离采空区下煤层开采时必须采取加强下伏煤层开采超前支护[5]；崔世荣提出采用“锚杆+工字钢+单体柱”联合支护方案[6].柳林某煤矿为近距离煤层开采，采用理论分析、数值模拟与现场监测相结合的方法，研究近距离煤层开采巷道支护方法，以保证煤层的安全高效开采。

1 工程概况

柳林某矿主采8#与9#煤层，其中8#煤层厚2.00～3.10 m，平均厚2.65 m，均为简单-较简单结构(夹矸数0～2)，煤层稳定，全区可采，顶板为灰岩，底板为泥岩。9#煤层厚1.55～3.00 m，平均厚2.17 m，煤层倾角1°～5°，为简单-复杂结构(夹矸数0～3)，煤层稳定，全区可采，顶板为泥岩，底板为细砂岩。两煤层间距11.45～19.6 m，平均间距13 m.

该矿主采8#煤层8107工作面与9#煤层9107工作面，其中工作面走向长785 m，倾向长167 m.107工作面东侧为8107工作面，南侧为采区轨道巷与皮带巷，其中8107工作面位于9107工作面与9105工作面之间，9105工作面东侧为8105采空区。两工作面位置关系见图1.

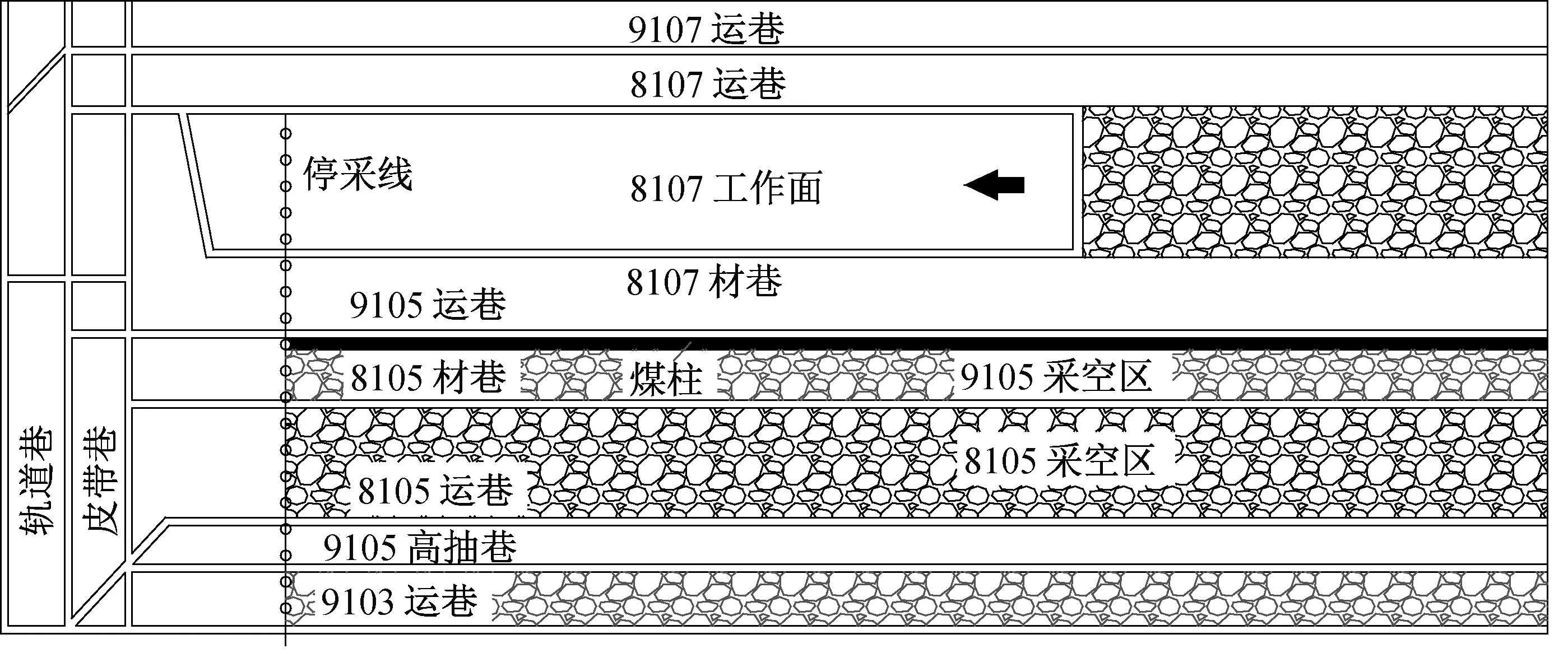
图1 工作面位置关系图

2 上覆煤层开采底板破坏深度分析

为研究上覆煤层开采对底板破坏程度，研究采用弹塑性力学理论[7]，构建底板破坏力学模型，见图2，可将底板破坏区域划分为3个应力影响区，即主动应力影响区、过度应力影响区及被动应力影响区。

根据图2力学关系得到如下表达式：

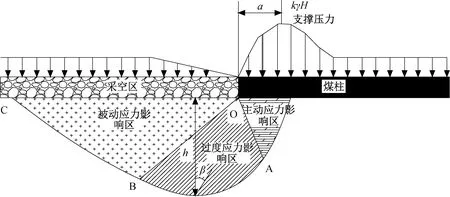
图2 底板破坏力学模型图

(1)

式中，h为底板岩层破坏高度，m；φ为底板岩层内摩擦角，(°)；a为煤柱破坏宽度，m；β为破坏深度垂线与煤柱边界夹角，(°).

令dh/dβ=0，可得：

(2)

结合式(1)、(2)得到底板岩层破坏深度：

(3)

根据极限平衡理论，煤柱破坏宽度表达式如下：

(4)

式中，m为采高，m；η为三轴应力系数；f为摩擦系数；k为应力集中系数；H为煤层埋藏深度，m；γ为顶板岩层容重，N/m3；φ1为底板岩层内摩擦角，(°)；C为煤层内聚力，MPa.

其中：

(5)

联合式(3)、(4)与(5)得到底板岩层破坏深度最大值表达式：

(6)

该矿8#煤层采高2.6 m，煤层内聚力为1.4 MPa，煤层及顶板岩层内摩擦角分别为30°与32°，摩擦系数为0.65，覆岩容重为24 500 N/m3；应力集中系数为4.65，8#煤层埋深300 m，将相关参数带入式(6)，可得底板岩层最大破坏深度为12.85 m.由于两煤层平均间距为13 m，在采动应力影响下，上煤层开采造成的底板岩层最大破坏深度基本达到了两煤层平均间距。为此，下煤层回采巷道可能会遭受采动影响，需要提前加强支护，保障巷道的稳定性。

3 回采巷道支护方案

3.1 支护参数的确定

根据悬吊理论，锚杆长度确定方法如下：

L=L1+L2+L3

(7)

式中，L1为锚杆外露长度，取0.1 m；L2为锚杆有效长度，需根据自然平衡拱理论确定；L3为锚杆锚固长度，取0.3～0.4 m.

当f≤3时，顶锚杆L2的长度确定方法：

L2=[B/2+Hcot(45+φ/2)]/f

(8)

式中，f为岩石硬度系数，取1.6；B为巷宽，取4.6 m；H为巷高，取2.7 m；φ为内摩擦角，取30°.

将相关参数带入式(8)，计算得到L2=2.3 m，即L=2.8 m，故顶锚杆长度取2.8 m.

对于帮锚杆长度，L2确定方法：

L2=2(1+f1)/(1+2f1)+(B-1)/(B+1)

(9)

式中，f1为煤硬度系数，取0.8.

将相关参数带入式(9)，得到L2=2.02 m，即L=2.52 m，故帮锚杆长度取2.6 m.

通过上述分析，确定巷道顶锚杆长度为2.8 m，直径为25 mm；帮锚杆长度为2.6 m，直径为20 mm.

设计选用锚索长度6 500 mm，索径21.8 mm，孔深为6 200 mm，间距为1 200 mm，此时锚索深度与间距应满足以下条件：

L/S≥2

(10)

式中，L为锚索孔深度，m；S为锚索间距，m.

经计算，该比值为5.2>2，即选用6 500 mm长度锚索能够满足要求。

3.2 巷道支护方法

8#煤层底板岩层破坏深度可能会对9#煤层回采巷道造成影响，为此提出对9#煤层巷道采取锚杆+注浆锚索联合支护方法。

巷道尺寸为4.6 m×2.7 m，在巷道顶板两帮各打1个锚杆，锚杆与水平夹角70°，巷道顶板中部打2个锚杆，杆径25 mm，长度2.8 m，采用全螺纹钢锚杆，锚杆间排距0.8 m；顶板4根锚杆间打3根注浆锚索，索径21.8 mm，长度6.5 m，主要目的在于利用浆体加固顶板岩层，锚杆索间距1.2 m，排距0.8 m；在巷道两帮每侧打4根锚杆，其中靠近巷帮中部打2根垂直壁面的锚杆，两侧锚杆沿壁面倾斜15°，锚杆间排距0.8 m，杆径20 mm，长度2.6 m.其中，巷道两帮锚杆采用W型钢带连接，顶板注浆锚索采用工字钢连接，注浆锚索拉张力为220 kN，浆体水灰比为0.7∶1，注浆压力3.5 MPa，巷道支护形式见图3.

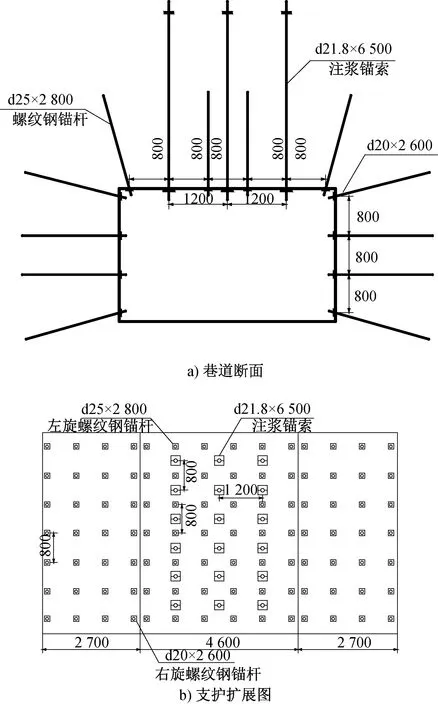
图3 巷道支护图

4 巷道支护数值模拟分析

4.1 数值模型构建

为了确定下煤层巷道支护方法的可靠性，采用FLAC3D数值模拟软件进行巷道支护稳定性分析，主要分析支护巷道的应力及位移变化情况。所构建的数值模型长350 m×宽60 m×高80 m，在模型两侧设计45 m边界宽度避免边界效应的影响，划分为35 580个单元，模型前后左右及下边界位移约束，在模型顶部施加约12.5 MPa的载荷等效上覆岩层容重，数值模拟用岩体力学参数见表1，所构建的数值模型见图4.

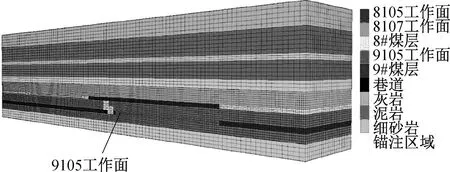
图4 数值分析模型图

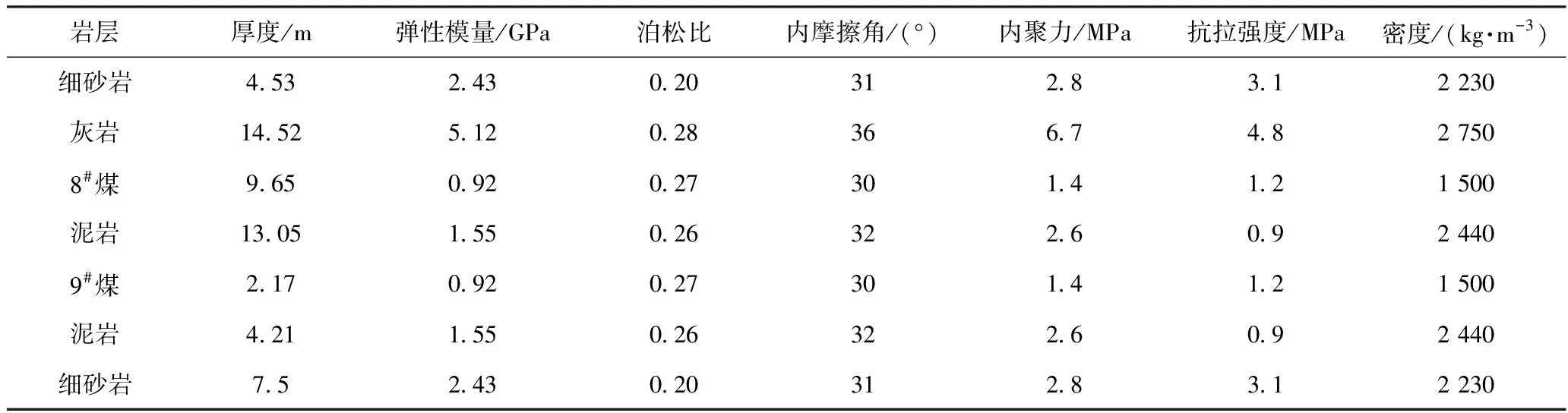
表1 岩体力学参数表

根据现场两煤层各工作面实际位置关系，将8#煤层的8105工作面、8107工作面及9#煤层的9105工作面顺次开挖，随后进行9105运巷的开挖及支护，对该运巷在研究提出的支护方法下所受垂直应力及位移变化情况进行分析。

4.2 数值结果分析

巷道塑性区分布情况见图5，由于两煤层间距较小，在上覆8#煤层工作面采动应力作用下，9105运巷已经产生了塑性破坏，巷道顶板主要为剪破坏，底板主要为拉破坏，巷道两帮顶底角位置塑性区范围较大。支护后巷道垂直应力变化情况见图6，通过锚杆+注浆锚索联合支护后，巷道顶底板存在一定范围应力降低区，顶板垂直应力为3.5 MPa，底板垂直应力为2.5 MPa，煤柱侧垂直应力为12 MPa，应力传播向采空区位置转移，有效减缓了对煤柱的冲击。

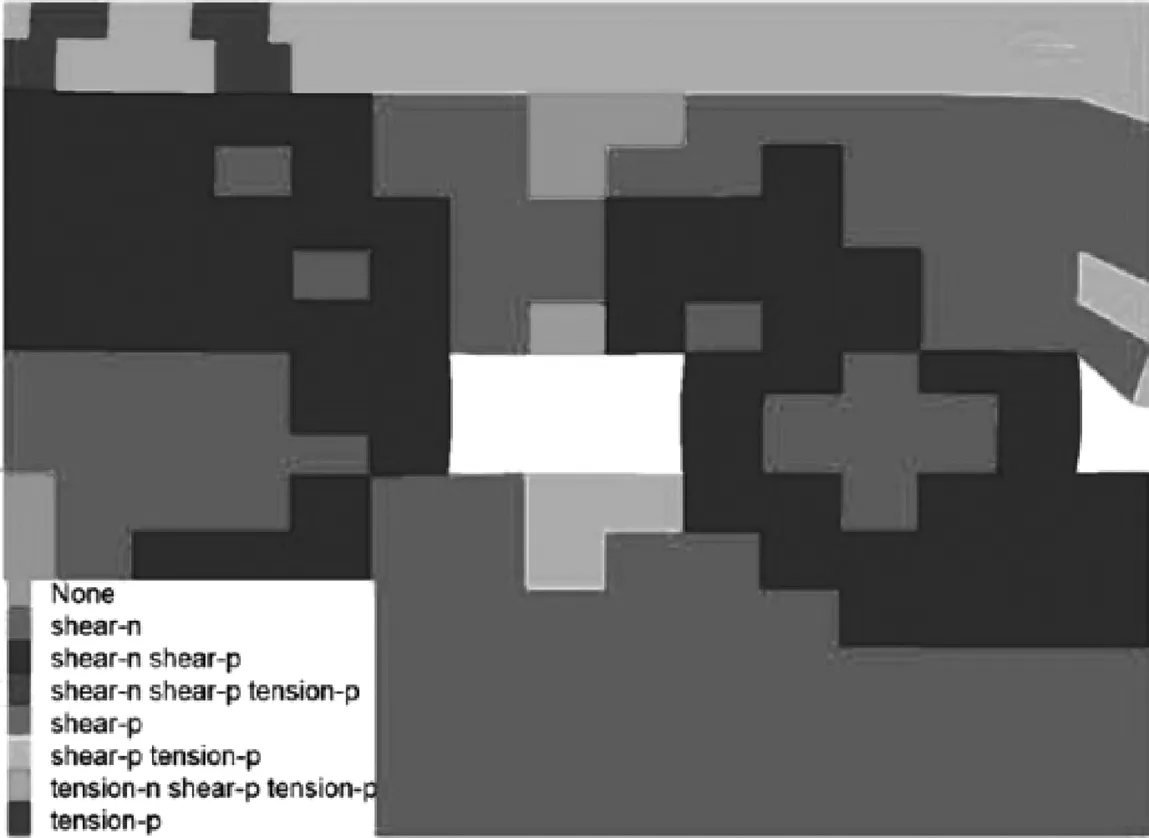
图5 巷道塑性区分布图

图6 垂直应力分布云图

巷道位移变化情况见图7.巷道顶板垂直位移约为45 mm，底板垂直位移约为35 mm，两帮垂直位移较小，约为5 mm(图7a))；对于巷道水平位移，煤柱侧约为43 mm，煤帮侧约为44 mm(图7b))，可以看出巷道两帮变形量相差较小，近似于对称变形发展。

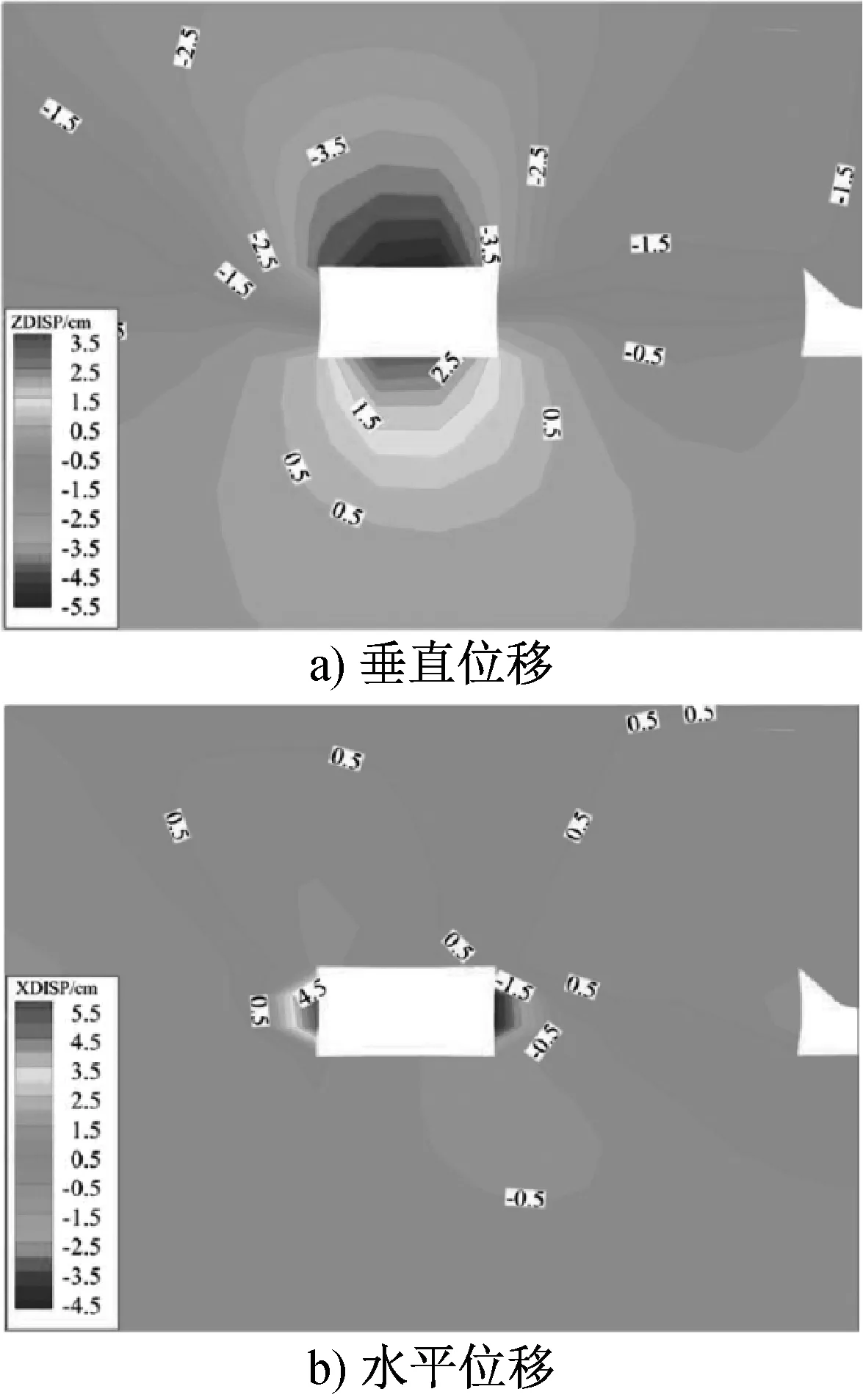
图7 位移分布云图

综合分析，巷道顶底板最大变形量约为45 mm，两帮最大变形量约为44 mm，采用锚杆+注浆锚索联合支护方法，可有效控制巷道顶底板及两帮变形，保障下煤层巷道的稳定性。

5 现场支护效果分析

为了验证该支护方案的有效性，在9#煤层9105运巷进行现场试验，并对巷道变形情况进行监测，监测点布置情况见图8.在工作面前方约260 m位置，布置3个测点，测点间距25 m，监测巷道两帮及顶底板位移变化情况，每个位置取3个测点的平均位移值进行分析，监测周期60 d.

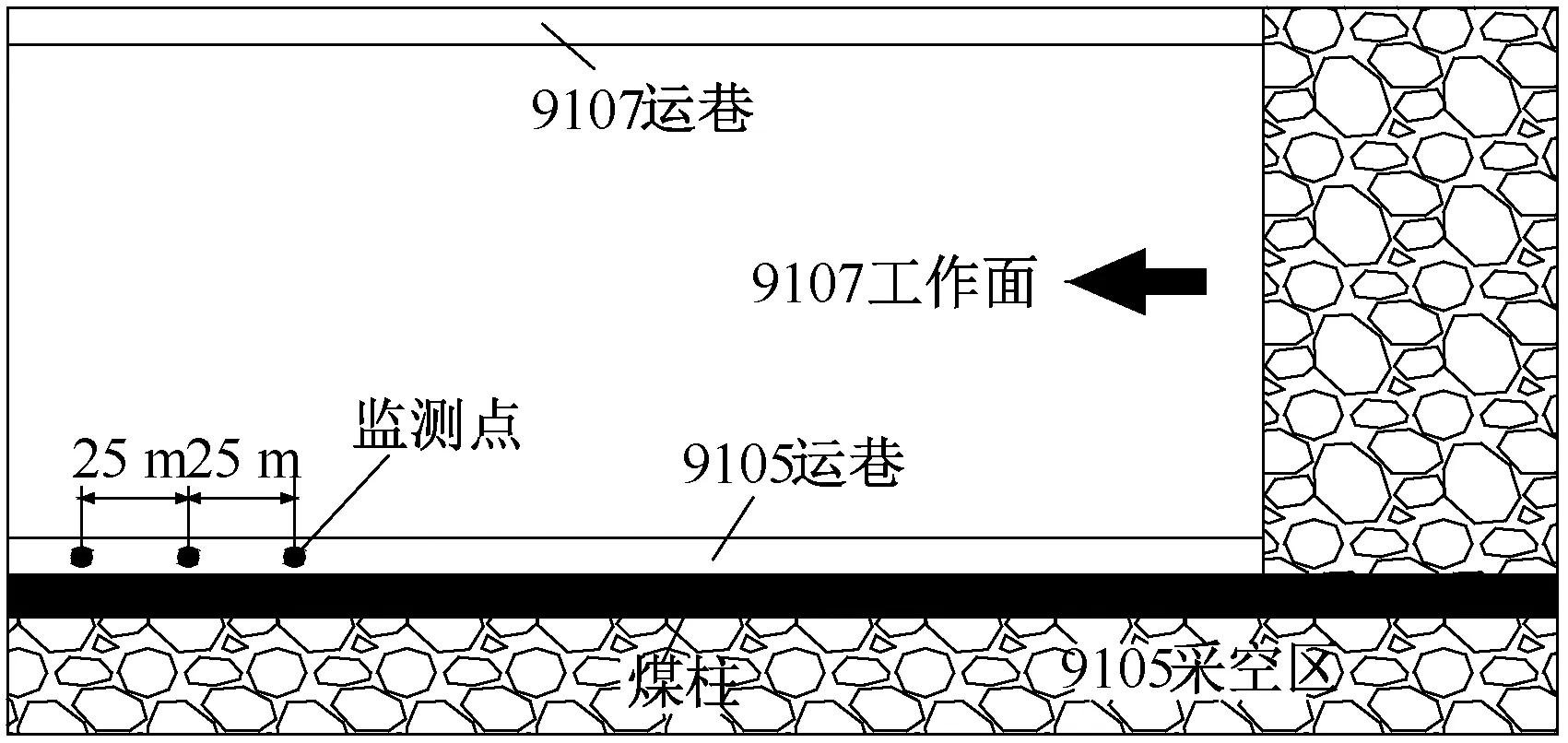
图8 监测点布置图

巷道变形监测结果见图9，随着工作面推进，巷道顶底板及两帮整体位移表现为先快速增加后缓慢增加特征，其中顶板最大垂直位移约为47 mm，底板最大垂直位移约为36 mm，两帮位移量比较接近，最大位移约为44 mm，这与数值分析结果基本一致。可以看出，采用锚杆+注浆锚索联合支护方法，有效控制了下煤层回采巷道变形发展，保障了巷道的稳定性。

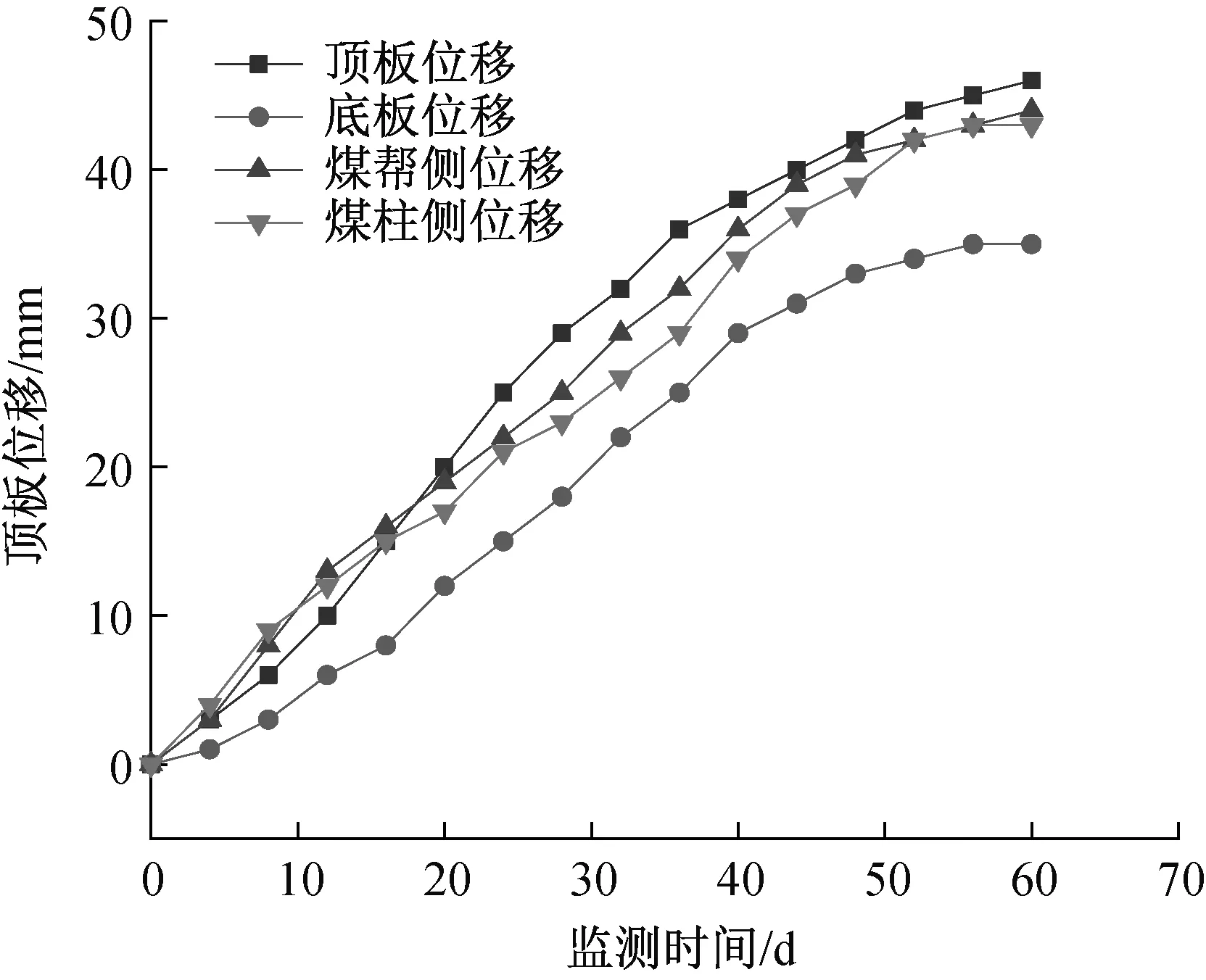
图9 巷道变形监测结果图

6 结 论

1)通过构建近距离煤层开采底板破坏深度力学模型，计算得到上煤层开采底板岩层最大破坏深度为12.2 m，已达到两煤层最小间距值，下煤层回采巷道可能会遭受上煤层采动影响，需要加强支护。

2)针对下煤层回采巷道，研究提出了锚杆+注浆锚索联合支护方法，给出了具体支护参数，通过数值模拟分析，该支护方案巷道顶底板最大变形量约为45 mm，两帮最大变形量约为44 mm，可有效控制巷道顶底板及两帮变形。

3)通过现场试验监测，巷道顶底板及两帮整体位移表现为先快速增加后缓慢增加特征，顶、底板最大垂直位移分别为47 mm与36 mm，两帮最大位移约为44 mm，保障了巷道的稳定性。