基于极值搜索算法的液压蝶阀系统PIλDμ参数整定

吴继伟，于春梅

（1.西南科技大学 信息工程学院，绵阳 621010；2.特殊环境机器人技术四川省重点实验室，绵阳 621000）

0 引言

液压蝶阀系统具有启闭扭矩大、压力损失-小、响应速度快等特点,被广泛应用于航空航天、工农业生产等各个领域[1,2]。实现该系统的快速控制具有十分重要的意义。

经典的PID控制方法结构简单、控制灵活,在液压蝶阀控制系统中被广泛使用[3]。但是液压蝶阀系统结构及组成极其复杂,是一个强非线性系统,传统的PID控制方法无法较好的完成液压蝶阀的控制。分数阶将分数阶微积分理论与PID控制方法结合,能够使控制系统获得更好的动态响应特性。文献[4]将分数阶PIλDμ引入地铁列车的速度控制,研究结果表明分数阶PIλDμ控制算法,可以使列车实现更优的速度控制和稳定性。文献[5]针对智能车高速行驶下对目标轨迹的快速跟踪要求,设计了分数阶PIλDμ控制器,仿真结果表明分数阶PIλDμ控制器具有比传统PID控制器更好的动态性能。

相比于传统PID控制方法,分数阶PIλDμ比整数阶PID控制器多了两个可调参数,使得分数阶PIλDμ控制器的参数整定变的更加复杂。对此,文献[6]采用遗传算法整定分数阶参数,仿真结果表明该方法能够完成分数阶PIλDμ参数的在线整定。但遗传算法计算复杂,难以处理其中非线性约束条件。文献[7]设计了一种基于神经网络的分数阶PIλDμ控制器,经过仿真验证,神经网络分数阶PIλDμ能够较好完成其参数的整定,但是神经网络算法对样本需求量大,而且对样本质量要求高,局限性比较明显。极值搜索算法是一种简单、高效、不基于模型的自适应算法,只需通过被控对象的输入输出,即可实时搜寻被控对象输出的极大、极小值。本文将极值搜索算法与分数阶PIλDμ相结合,提出了一种基于极值搜索算法的PIλDμ参数整定方法。同时,为了更好地验证该算法的有效性,结合ADAMS、UG、AMEsim三种软件对液压蝶阀控制系统进行建模。AMEsim和MATLAB/Simulink联合仿真结果验证了本文的有效性。

1 极值搜索算法

极值搜索算法是由Tsien教授于1954年提出的一种自适应控制方法[8],能够在某些信息未知的情况下根据输出、能耗等条件使系统获得满意控制效果。其中基于扰动的极值搜索算法是极值搜索算法中常用的一种控制方法,该方法只需要根据系统的扰动以及合适的滤波器就可以获得系统梯度信息[9]。以基于摄动的单变量极值搜索算法为例。

图1为基于摄动的极值搜索算法原理图。算法的目的是调节θ使得f(θ)取极小值。算法通过探测信号的扰动获取目标函数的梯度信息,并沿着负梯度方向进行搜索,寻找目标函数的极值。然后根据该梯度信号对控制器参数的最优值不断进行在线搜索[10]。

图1 基于摄动的极值搜索算法原理图

假设目标函数f(θ)具有如式(1)的二次形式：

其中f(θ)是需要极小化的输出：f*为需要搜索的最小值,f"为函数f(θ)的二阶微分。θ*为使得f(θ)达到最小的最优参数；θ是实际输入参数；k是调节积分环节的自适应增益；a是探测信号的幅值；ω为探测信号的频率；为高通滤波器。

将输入参数代入式(6)：

利用基本的三角恒等关系展开式(4)得到：

经过高通滤波器,滤除直流信号可得f*可得：

加入乘法信号sinωt得到：

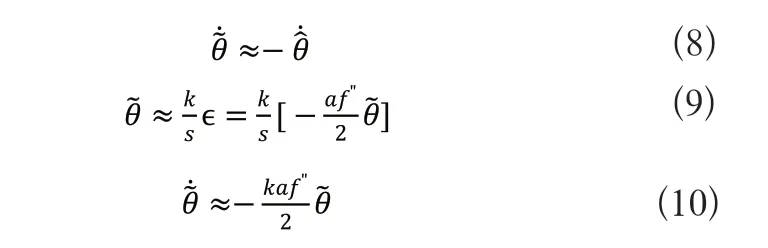
由式(10)可知,当选择适当的增益k和振幅a,随着迭代次数的增加,极值搜索算法会使输入信号与最优输入的估计误差逐渐衰减到0。

2 控制器设计与系统建模

2.1 基于极值搜索算法的PIλDμ参数整定方法

分数阶PIλDμ将传统的PIλDμ法扩展到分数阶领域[11]。与传统的PID方法相比,该方法新增了积分阶次λ、微分阶次μ两个参数,使其有更大的参数调节范围,拥有比传统PID更好的控制效果。但是分数阶PIλDμ参数整定比较困难。因此,本文将极值搜索算法与分数阶PIλDμ控制算法相结合,利用极值搜索算法在线调整PID控制器参数,使整个系统跟踪误差最小,图2是基于极值搜索算法的参数整定方法原理框图。使用误差平方积分准则函数ISE为目标函数J(θ)[12]。

图2 基于极值搜索算法的PIλDμ参数整定方法原理框图

其中e为闭环输入与输出的误差,θ为分数阶PIλDμ控制参数。通过极值搜索算法的极值寻优能力,在线调整分数阶PIλDμ参数,使目标函数J(θ)达到最小值。完成分数阶PIλDμ参数的自整定。

2.2 系统建模

液压蝶阀系统控制框图如图3所示,整个系统由液压伺服执行器、蝶阀及传动机构组成。

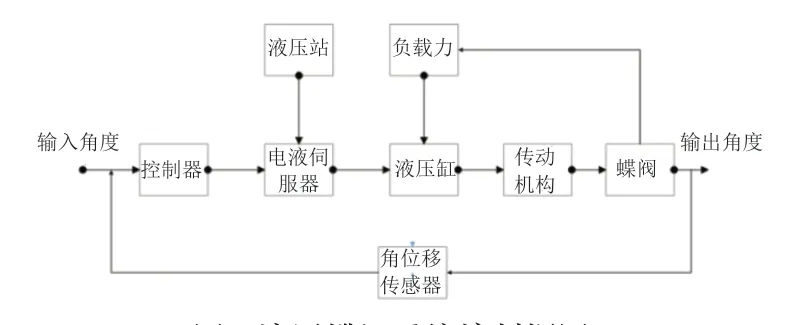
图3 液压蝶阀系统控制框图

该系统的传动机构为曲柄连杆式装置,该装置可以得到更好的角度控制精度,但是会导致整个传动机构运动轨迹及受力情况变得十分复杂,常规的数学分析方法难以分析整个传动过程。针对这一问题,本文首先利用UG软件建立各零件模型,根据实物模型组装成装配体,如图4所示。

图4 传动机构及蝶阀三维模型

然后将UG软件建立的模型以.xt格式导出。使用ADAMS软件对该模型进行仿真分析,得到系统中液压杆的伸长量与蝶阀转动角度和液压杆受力相关数据,使用最小二乘的方法完成数据的拟合。得到液压杆伸长量与蝶阀转动角度关系曲线、液压杆伸长量与液压杆受力关系曲线,如图5、图6所示。

图5 液压杆伸长量与液压杆受力关系曲线

图6 液压杆伸长量与蝶阀转动角度关系曲线

最后通过对整个液压伺服系统的分析,利用AMEsim软件建立了电液伺服系统所有重要部件模型,如油箱、电机、电磁溢流阀、电液伺服阀、液压缸等部件。加入传动机构数据完成整个液压蝶阀控制系统模型的建立。图7为AMEsim-Simulink联合仿真中电液伺服系统AMEsim模型。

图7 电液伺服系统AMEsim模型

2.3 AMEsim-Simulink联合仿真

AMEsim软件可以建立更加精确的液压伺服系统模型,在MATLAB软件中更适合控制算法的设计与仿真。利用AMEsim和Simulink的联合仿真技术可以充分发挥两种软件的优势[15]。本文在AMEsim软件中建立液压伺服系统模型,在MATLAB软件中完成基于极值搜索算法的分数阶PIλDμ参数整定方法的设计。通过S-function接口将两个软件联合在一起,完成整个控制系统的设计与仿真。

3 实验结果分析

3.1 基于极值搜索算法的PIλDμ参数整定

首先将本文分数阶PIλDμ参数整定方法中θ参数λ、μ设置为定值1,利用极值搜索算法只整定PID的三个参数值。其目标函数J(θ)及PID参数整定曲线如图8、图9所示,从图中可以看出PID三个参数在经过3.7秒后从0逐渐稳定到12、0.07、0.6左右。同时目标函数J(θ)随着PID参数的整定最终趋于0值。图10是系统阶跃响应图,由图可知,PID控制方法在经过极值搜索算法在线整定参数后能较好的完成液压蝶阀系统的控制。

图8 目标函数J(θ)

图9 PID参数整定曲线

图10 系统阶跃响应

3.2 基于极值搜索算法的分数阶PID参数整定

使用极值搜索算法整定分数阶PIλDμ参数,从图11中可以看出分数阶PIλDμ参数P、I、D、λ、μ五个参数在3.4秒后分别整定到11.2、3.3、0.08、0.4、1左右。由图12可知,其目标函数J(θ)也最终收敛到0值附近。图13显示出参数调整后的分数阶PIλDμ具有较好的控制效果。

图11 PIλDμ参数整定曲线

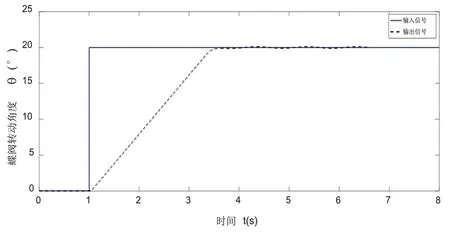
图12 系统阶跃响应

图13 目标函数J(θ)

3.3 不同控制方法的控制效果比较

为了研究分数阶PIλDμ与传统PID控制效果的区别和极值搜索算法参数整定与参数优化能力,本文将通过经验调整参数的PID、基于极值搜索算法的PID、基于极值搜索算法的分数阶PIλDμ、初始化参数的极值搜索PID、初始化参数的极值搜索分数阶的控制效果作对比。不同控制方法的控制效果如图14所示。

从图14中可以看出,通过经验调整参数的PID控制效果十分不理想,跟踪速度慢且存在超调。将极值搜索算法应用于PID、分数阶PIλDμ参数调整中,可以看到其控制效果有了明显的提升。分数阶PIλDμ比普通PID多了两个参数,从图14中可以看出分数阶PID比普通PID具有更好的控制效果。

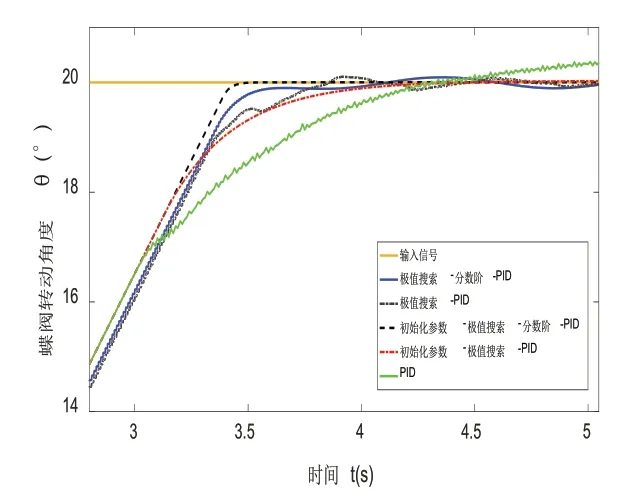
图14 不同控制方法控制效果局部放大图

由于极值搜索算法参数是从零开始整定的,其整定过程需要较长的时间。从图14可以看出,相比于通过经验调整参数的PID,基于极值搜索算法的PID、分数阶控制效果曲线会有一定的滞后。将通过经验调整的PID参数初始化于极值搜索算法中,从图14中可以看出初始化参数的极值搜索PID、分数阶PIλDμ具有更好的控制效果,验证了极值搜索算法的参数寻优能力。

在实际工作情况中,阀门需按照给定的斜坡信号动作。因此这里将输入设定为斜坡信号,从图15中可以看出基于极值搜索算法的分数阶PIλDμ控制方法能够较好的完成液压蝶阀控制系统动作要求。

图15 斜坡信号跟踪图

4 结语

本文将分数阶PIλDμ控制方法运用于液压蝶阀控制系统中,并利用极值搜索算法对其参数进行整定,同时,为了更好地验证算法的有效性,结合三种软件建立了液压蝶阀控制系统的仿真模型。经仿真验证,极值搜索算法能较好的完成PID、分数阶PIλDμ的参数整定与参数寻优。相比于传统PID算法,基于极值搜索算法的分数阶PIλDμ能更好的完成液压蝶阀系统的控制。