基于多目标的九轴五联动磨床整机分析与结构优化

梅益，薛茂远，甘盛霖，罗宁康，唐方艳，肖展开

（贵州大学机械工程学院，贵州贵阳 550025）

九轴五联动数控缓进给磨床样机在进行加工验证后，发现存在产品不良频率高、生产精度难以保证等问题，有必要针对磨床的整体结构及相应结构参数进行优化［1-2］.结构优化方法有很多，比如Yun T等对一种飞机零件加工机床的头架结构进行拓扑优化，实现高刚度、低振动和轻量化的目标［3］.Besharati等对龙门机床采用层次分析法、多目标遗传算法进行多目标选择与优化［4］.但这些优化方法运用有限，目前人工神经网络具有很强非线性函数拟合能力，可以拟合变量与质量指标之间非线性耦合关系，再用优化算法对此网络模型寻优，能得到较优的工艺［5-6］.本文利用Ansys Workbench 软件对磨床整机进行动静态特性分析与优化，同时结合灵敏度分析对原有结构进行改进，整机的一阶固有频率和最大静变形得到很大改善.再以整机一阶固有频率、最大静变形及整机质量为优化质量指标，使用灰色关联分析法将转成综合目标灰色关联度，再利用GAELM-GA 对该磨床改进后的主要结构参数进行优化，优化后改进后的九轴五联动磨床的一阶固有频率、最大静变形及整机质量得以一定改进，验证了该多目标优化方法的有效性.结构改进及优化方法为后续制定新的磨床提供理论参考.

1 磨床关键零部件参数化建模

1.1 九轴五联动数控磨床样机运动分析

研究的磨床为某公司生产的MKH7150WJ 九轴五联动数控缓进给磨床样机，如图1 所示，初始定位精度0.003 mm.为了减少分析时间，忽略螺钉孔、圆角以及部分凸台等对分析结果影响不大的因素，将结构复杂却不需要进行细致分析的组件移除.采用等效力的方式体现在有限元分析环节，提升整个工作效率［7-10］，磨床的三维模型简化后如图2 所示.磨床结构主要由床身、立柱、主轴箱、工作台和摇篮式工作台等零部件组成，床身与工作台、床身与立柱及立柱与主轴箱之间均通过滑块与滚珠丝杠体分别实现横向（X轴）、纵向（Y轴）及垂向（Z轴）三个方向上的运动，并通过摇篮式工作台实现两个旋转轴（A轴、C轴）方向的运动，如图3所示.

图1 九轴五联动数控缓进给磨床样机Fig.1 Prototype of nine-axis five-linkage CNC slow feed grinder

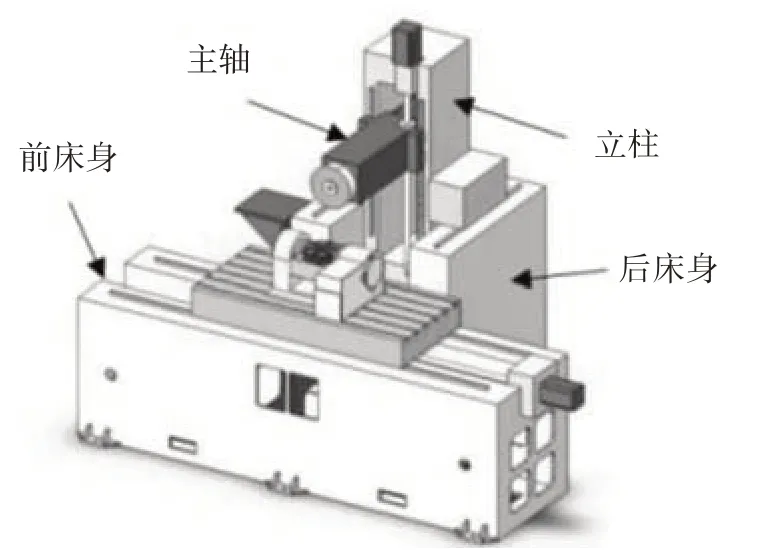
图2 三维模型简化Fig.2 3D model simplification

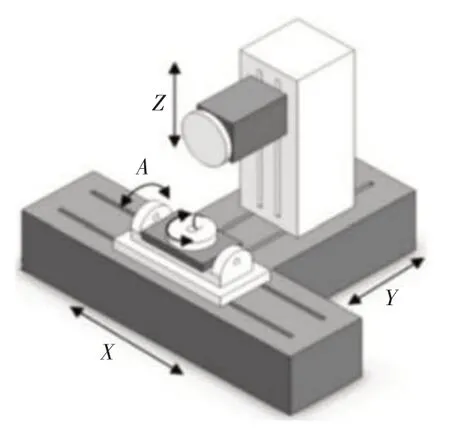
图3 九轴五联动磨床运动分析Fig.3 Movement analysis of nine-axis five-linkage grinder

1.2 主轴的参数化建模

主轴的设计是经过严格的验证得到的最佳方案，因此仅在有必要进行改进的情况下对主轴箱与立柱连接部分的高度HD进行改进并参数化设置，便于满足实际加工条件，主轴部件结构如图4所示.

图4 主轴部件结构Fig.4 Spindle component structure

1.3 立柱的参数化建模

立柱左右两侧内部布置有5 块垂向筋板，横向布置有10块横筋板，如图5所示，采用这种格栅式筋板布置方式能有效地解决立柱参数的修改问题.

图5 立柱各筋板位置尺寸Fig.5 Position size of each rib of the column

1.4 床身的参数化建模

床身内部布置有7 块筋板，其中前磨床床身有5块纵筋板，后磨床床身有2块横筋板，如图6所示.采用布置筋板的方式，能有效地解决减少床身质量与提高床身稳定性之间互相矛盾的问题.

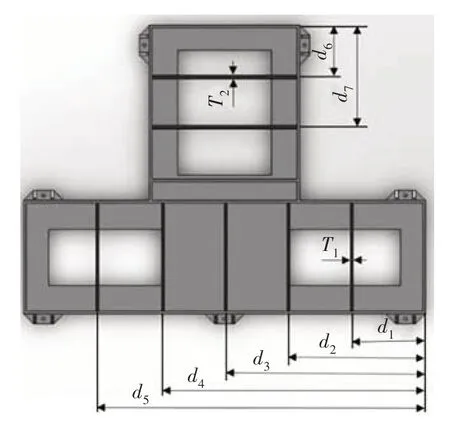
图6 床身各筋板位置尺寸Fig.6 The position and size of each rib of the bed

2 磨床整机静力学及模态分析

2.1 磨床整机应力分析

由图7 可知，在模拟的实际加工工况下，磨床应力主要分布在中心加工位置，其最大应力7.4952 MPa远低于材料的屈服应力250 MPa，后续优化不再讨论磨床整机等效应力，在实际加工过程中不会因应力集中而发生局部破坏.设计时可以进行轻量化处理.

图7 磨床整机等效应力云图Fig.7 Equivalent stress cloud diagram of the whole grinder

2.2 磨床整机刚度分析

由图8 可知磨床整机的z方向变形量大于x、y方向的变形量，主要是由于径向磨削力引起的，也是影响整体变形量大的主要原因.有必要对整体结构改进，降低整机变形，使刚度分布相对更均匀.

图8 磨床整机刚度分析Fig.8 The stiffness analysis of the whole grinder

2.3 磨床整机模态分析

图9 为磨床整机模态分析，磨床整机的前六阶固有频率为：63.724 Hz、83.128 Hz、94.907 Hz、119.36 Hz、124.94 Hz、126.04 Hz，其一阶振型为立柱主轴部分沿纵向摆动.其一阶固有频率大于主轴自转所能产生的最高频率50 Hz.因此在实际加工过程中并不会产生共振情况，整机具有良好的动态性能，但一阶固有频率高出主轴自转所能产生的最高频率不是太多，还是应该尽可能提升整机的一阶固有频率.

图9 磨床整机一阶振型Fig.9 The first-order vibration mode of the whole grinder

3 基于灵敏度分析的磨床零部件改进

3.1 主轴部件结构改进

将主轴相关参数导入Direct Optimization 模块进行寻优分析，生成的部分数据及对应解如表1 所示.只有一个参数作为变量进行分析，其对各目标的灵敏度均为1，结合表1 可以得出，当主轴箱高度增加，主轴部件与立柱间作用点距离变大，其作用力减小对主轴部件自身的固有频率及最大静变形都有不同程度改善.主轴箱内部结构复杂，简单地增加主轴箱高度HD并不符合实际情况，因此采用局部改进的方法，通过设置加强筋的方式，增加主轴箱尾部高度，并将侧面也修改为筋板式，在增高尾部引起主轴箱质量增加的同时，也在侧面进行优化以减小一些主轴箱质量，改进后的主轴部件与原方案对比如图10所示，将增加的主轴箱尾部上下高度参数H1、H2作为后续优化变量，如图11 所示，目的在于提升主轴部件自身的固有频率，降低其最大静变形.

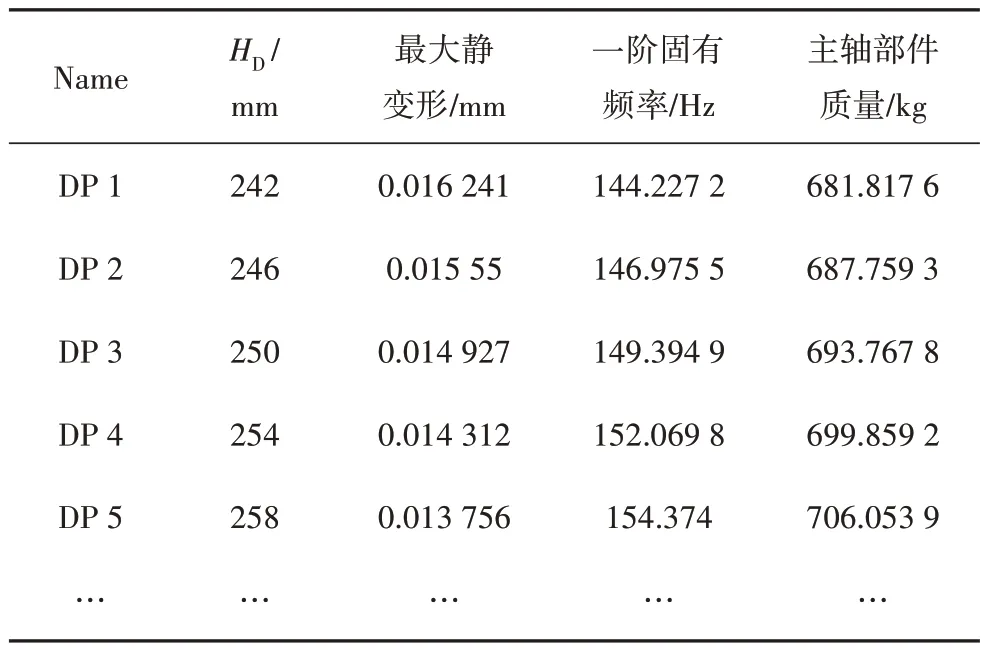
表1 主轴部件部分数据及对应解Tab.1 Partial data and corresponding solutions of spindle parts

图10 改进前后主轴部件示意图Fig.10 Schematic diagram of the spindle components before and after the improvement

图11 主轴箱处设计变量Fig.11 Design variables at the headstock

3.3 立柱结构改进

将立柱相关参数导入Direct Optimization 模块进行寻优分析，经计算生成的部分数据组及其对应解如表2 所示，同时筛选出表3 最佳多目标优化解集，根据多目标优化结果均值取整导入后续的结构分析［11-12］，其中各个变量对各目标函数的灵敏度如图12所示.

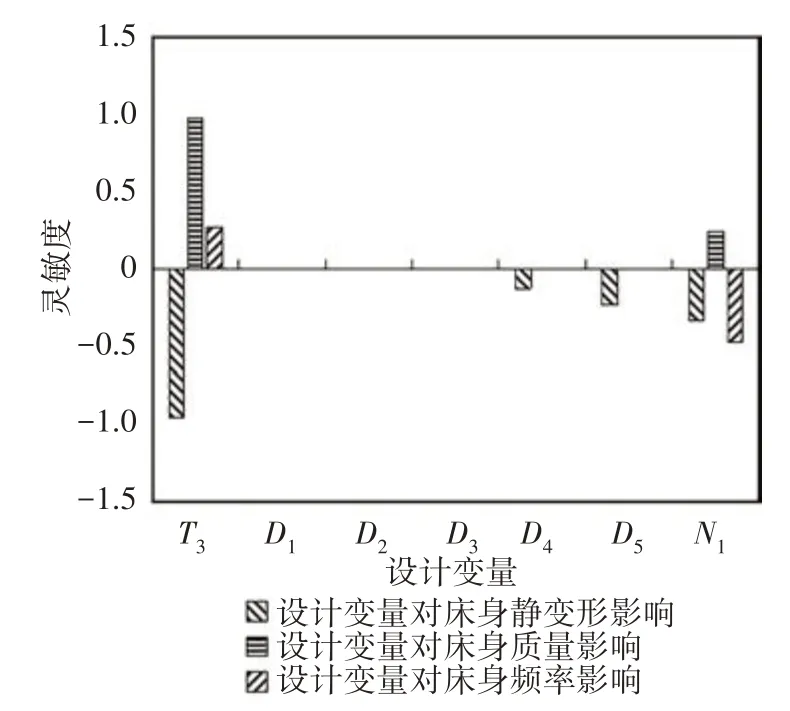
图12 立柱各变量对质量指标的灵敏度Fig.12 Sensitivity of each variable of the column to each quality index

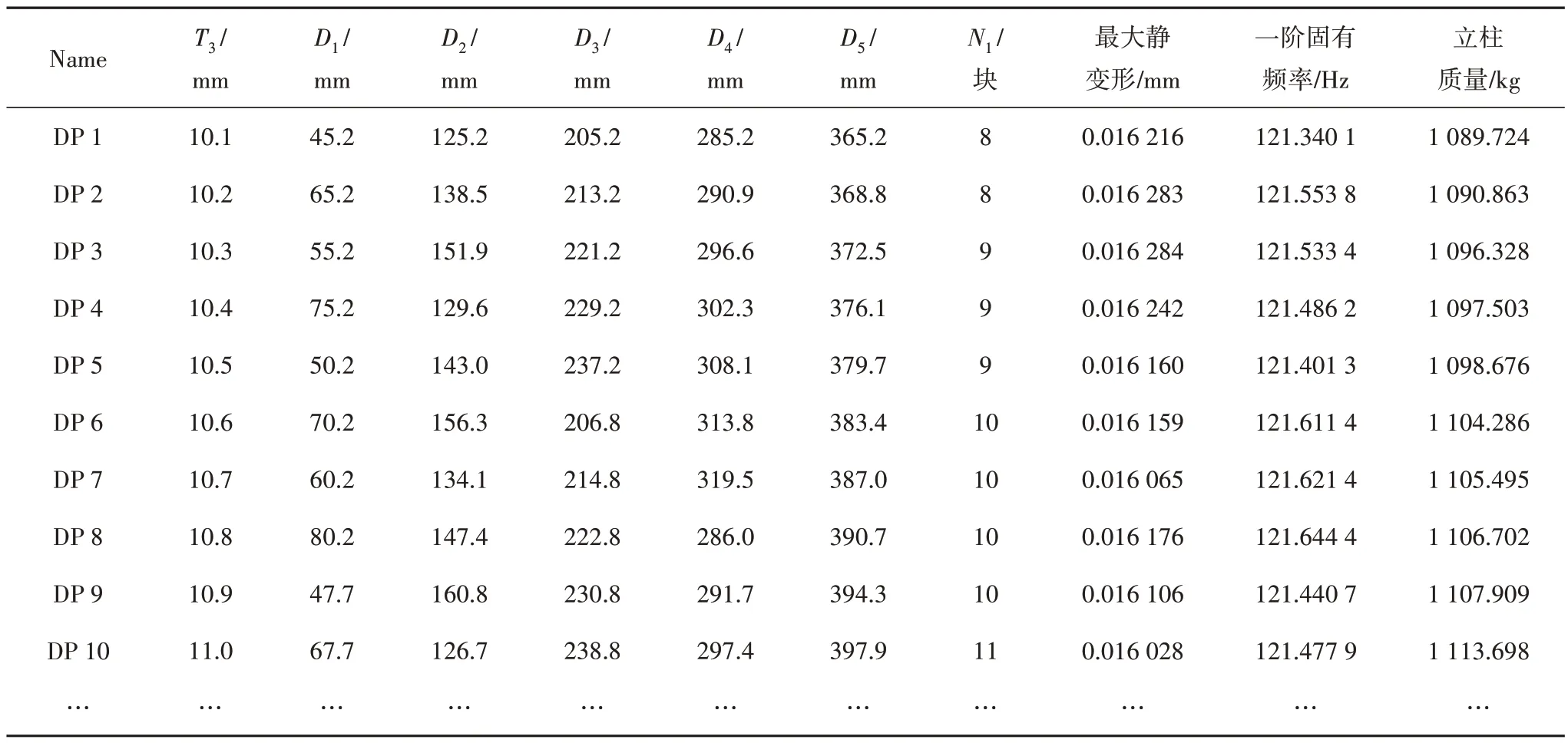
表2 立柱部分数据组及对应解Tab.2 Some data sets and the corresponding solutions of the column

表3 最佳多目标优化解集Tab.3 The best multi-objective optimization solution set

由图12 可知，立柱整体质量会随着筋板厚度T3及均布横向筋板数量N1增加而增加，T3对床身的最大静变形、整体质量及一阶固有频率有很大影响，选择T3作为后续优化参数.立柱部分尺寸T3、D4、D5与N1对最大静变形存在一定影响，但结合表2 的分析数据来看，其尺寸变化对于静变形的影响程度很小，且对于一阶固有频率来说，大部分尺寸与一阶固有频率大小几乎无关，由此可见，立柱内部筋板布置情况对于立柱部件结构的最大静变形及一阶固有频率影响很小，只是简单地对其进行增加或减小没有太大意义.为了减小变形，增大一阶固有频率，选择在立柱两侧中上位置增设加强筋，同时将加强筋厚度T4与T5作为后续优化目标，如图13所示.

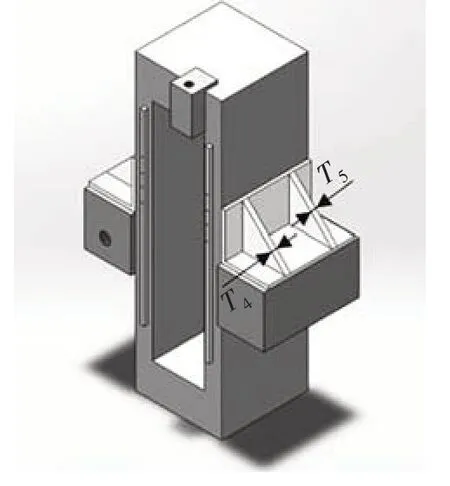
图13 改进后立柱结构Fig.13 Improved column structure

3.3 床身结构改进

基于Direct Optimization 模块，根据床身相关参数设定100 组解集进行寻优分析，其生成的部分数据组及对应解如表4所示，同时筛选出表5最佳多目标优化解集，根据多目标优化结果均值取整导入后续的结构分析，各个变量对目标函数的灵敏度如图14所示.

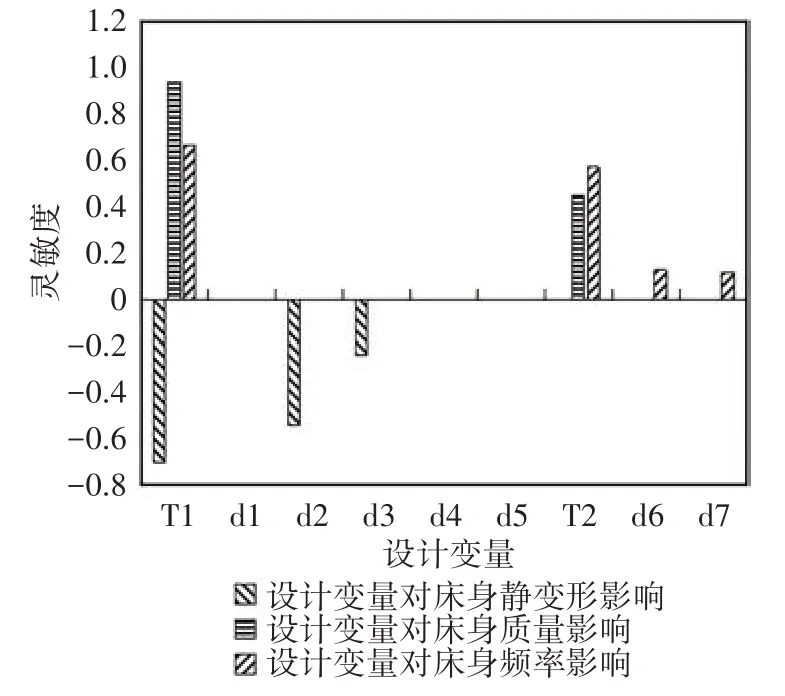
图14 床身各变量对各质量指标的灵敏度Fig.14 Sensitivity of each variable of the bed to each quality index

表4 床身部分数据组及对应解Tab.4 Some data sets and the corresponding solutions of the bed

表5 最佳多目标优化解集Tab.5 The best multi-objective optimization solution set

由图14 可知，床身整体质量会随着筋板厚度增加而增加，床身部分尺寸T1、T2、d2与d3对最大静变形具有不同程度的影响，T1、T2、d6与d7对一阶固有频率具有显著影响，故应当对前床身与后床身的尺寸进行优化.T1与T2对床身的最大静变形、整体质量及一阶固有频率有很大影响，选择T1与T2作为后续优化参数.除了对筋板尺寸优化外，还应对磨床后床身结构进行相应优化，结合实际需求，将筋板数量N作为后续优化目标，以此来提升磨床后床身整体结构强度，目的在于提升其一阶固有频率.如图15所示.

图15 床身结构改进Fig.15 Improved bed structure

3.4 改进后的整机模型

对改进后的整机模型进行动静态分析，如图16所示.在对磨床关键零部件进行改进后，虽然磨床整体质量增加了11.68%，但其最大静变形减小28.83%，一阶固有频率提升31.28%，提升了磨床的工作精度与性能.

图16 改进后磨床整机动静态分析Fig.16 The dynamic static analysis of the improved grinder

4 基于灰色关联分析及GA-ELM-GA 的磨床整机多目标优化

磨床的结构复杂，若只是对组成磨床的各个关键零部件进行改进，无法有效地对磨床整体结构性能进行加强，因此应结合磨床关键零部件改进及分析情况，对磨床整机的相关工艺参数进行多目标优化，才能得出具有实际意义的优化方案［13-14］.根据上文分析设置了表6参数及其取值范围.

表6 整机参数及其取值范围Tab.6 Machine parameters and their range of values

4.1 灰色关联分析

灰色关联分析可以对多目标问题进行综合评价，从而将多目标优化问题转换为单目标问题进行研究.主要步骤如下［15-17］：

1）确定比较系列Yi(k)与参考系列式Y0(k).

2）本文的最大静变形与整机质量要求越小越好，使用望小公式归一化处理，如式（1）.一阶固有频率要求越大越好，使用望大公式归一化处理，如式（2）.

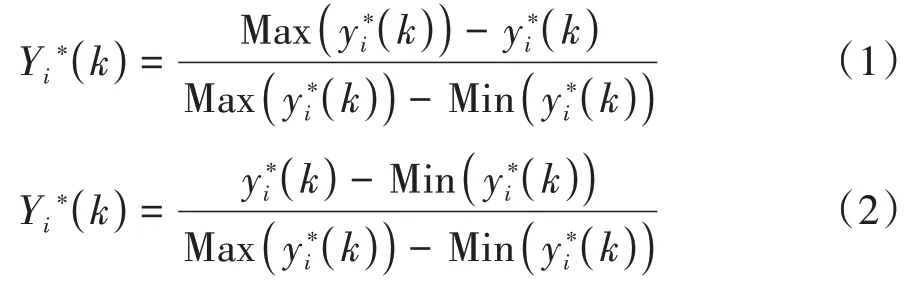
3）求灰色关联系数ξi(k)，如式（3）.

式（3）中：Δi(k)为差序列，Δ max、Δ min 为差序列的最大差与最小差，ρ为分辨系数，一般ρ=0.5.

4）计算灰色关联度γ，如式（4）.

式（4）中：γ为灰色关联度，wj表示各质量指标的权重系数，本文j=3.

wj可由变异系数法求得［18］.变异系数法计算权重如式（5）.

式（5）中：Vj表示第j个质量指标的变异系数；σj表示第j个质量指标的标准差；-xj表示第j个质量指标的平均值；γj表示第j个质量指标权重系数.

通过ANSYS 的Optimal Space-Filling Design 对表6变量相应的范围生成500组的样本，通过上述步骤将整机质量、最大静变形及一阶固有频率三个质量指标转成综合目标灰色关联度.

4.2 GA-ELM-GA 优化模型

极限学习机（Extreme Learning Machine）有较强的非线性拟合能力，但由于ELM 输入层与隐含层之间的权值矩阵w及隐含层神经元的阈值矩阵b随机产生，导致网络模型的预测拟合能力及预测稳定性不足.使用遗传算法寻找最优的w与b，得到预测能力及稳定性好的GA-ELM 网络预测系统，此系统可以较好反映磨床工艺参数与综合目标灰色关联度之间非线性耦合关系，最终再通过遗传算法（GA）在训练好的GA-ELM 网络预测模型中寻找最优磨床工艺参数［19-21］.

GA-ELM-GA 优化模型算法步骤如下：

1）输入500 组样本数据，归一化处理，选择样本前400 为训练样本，后100 为测试样本，设置ELM 网络模型的迭代次数100，种群大小50，隐含层神经元个数17.

2）利用遗传算法全局寻优能力寻找最佳的权值w与阈值b，在种群初始化阶段随机取权值w与阈值b，通过反复选择，交叉，变异等操作，获取最优的w与b.

3）将GA 优化的权值和阈值传回ELM 网络，得到GA 优化的ELM 网络模型，分析预测值与测试值之间的误差，检查系统预测精度.

4）通过遗传算法在训练好的GA-ELM 网络预测模型中寻找最优工艺参数.确定遗传算法的优化目标为灰色关联度γmin、优化变量及其约束范围.利用遗传算法强大的全局寻优能力寻找训练好的GAELM 网络模型的最小翘曲变形及对应的工艺参数.将训练好的GA-ELM 网络模型预测输出作为个体适应度值，根据适应度值大小筛选出灰色关联度γ最小个体，淘汰较差个体.通过选择、交叉、变异等操作寻找最优工艺参数.建立的遗传算法数学模型如式（6）［22］.

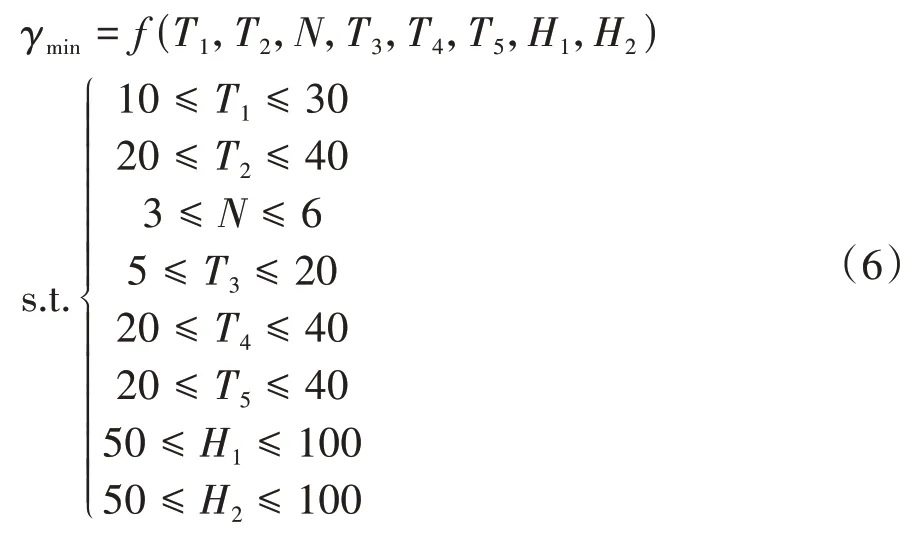
式（6）中：f(T1，T2，N，T3，T4，T5，H1，H2)为遗传算法的适应度函数.

4.3 GA-ELM 预测结果

图17 为ELM 与GA-ELM 网络预测结果对比，可以看到直接使用ELM 网络模型预测时，R2=0.801 23，均方误差为0.000 984 37，预测精度不够，而使用GA-ELM 网络模型预测时，R2=0.965 41，预测精度得到很大提升，且相对误差大部分控制在5%以内，此GA-ELM 网络模型作为预测模型可以较好反映磨床工艺参数与灰色关联度之间非线性耦合关系.可以用于后续GA寻优的预测模型.

图17 ELM与GA-ELM网络预测结果对比Fig.17 Comparison of network prediction results between ELM and GA-ELM

4.4 GA-ELM-GA 寻优过程与结果

利用GA 对GA-ELM 进行全局极值寻优，图18为GA 寻优适应度曲线，迭代约70 代后，磨床的综合评价指标灰色关联度收敛于0.5926 处，对应的尺寸T1为11.35 mm，T2为39.57 mm，N为4 块，T3为6 mm，T4为35.37 mm，T5为37.42 mm，H1为85.43 mm，H2为52.32 mm.

图18 适应度曲线Fig.18 Fitness curve

4.5 模拟验证

将GA-ELM-GA 优化后8 个磨床结构工艺参数导入ANSYS Workbench 仿真平台进行验证，如图19所示.得到图20 磨床整机优化后的最大静变形、整机质量及一阶固有频率，可以看到：GA-ELM-GA 优化后九轴五联动磨床的整机质量与原始方案相比增11.68%，最大静变形减小29.68%，一阶固有频率提升了34.71%.

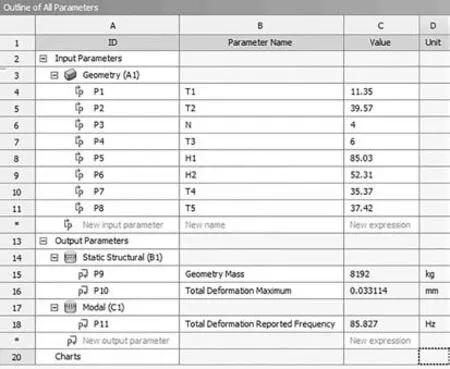
图19 ANSYS Workbench参数输入及其对应指标Fig.19 ANSYS Workbench parameter input and its corresponding index

图20 参数优化后磨床整机动静态分析Fig.20 Static analysis of the whole machine after parameter optimization

5 模拟改进后新产品试制方案

结合结构优化及多目标优化结果，与实际相结合对磨床进行对比分析，得出用于新一代基础缓进给磨床试制的参考，并已初步完成了新一代样机试制，具体说明如下：

1）主轴箱在进行铸造后，用于带砂轮修整装置的磨床结构当中，如图21 所示，其砂轮修整结构安装在主轴上方，其重量会平衡一部分径向磨削力带来的Z方向的变形，相当于增设尾部加强筋，还采用了文中的增加尾部滑块距离，牺牲一部分Z方向行程，来达到减小作用力的效果，相当于文中通过改进主轴箱尾部以减小最大静变形、增加磨床静刚度的改进方式.

图21 样机磨床主轴Fig.21 Prototype grinding machine spindle

2）通过分析得出，立柱结构的改进对于其最大静变形影响是很大的，因此，从提升磨床静刚度角度出发，有必要对立柱进行更为完善的改进.从文中有限元分析结果可知，现有的磨床立柱内部筋板的格栅式布局对立柱性能方面影响不大，文中仅是进行了轻量化处理，在进行综合考虑以后，实际样机还对内部筋板进行了重新设计，同时也参考文中对立柱侧面与立柱托板结合处的加强取得的显著效果，对该部分结构进行了加强处理，如图22所示.

图22 样机磨床主柱Fig.22 Prototype grinding machine column

3）图23 为现场在整机安装前，仅安装磨床床身、立柱及主轴部件时照片，对磨床后床身进行了改进，从图中可以看到后床身部分筋板进行了增多，其主轴部件尾部也进行了相应的加高处理，且改进后的磨床选用了技术指标更为优异的丝杠、导轨等部件.图24 为磨床定位精度测试图，定位精度由原来的0.003 mm变成0.0014，其性能得到明显提升.

图23 样机磨床床身安装图Fig.23 Prototype grinder bed installation drawing

图24 样机磨床定位精度测试Fig.24 Positioning accuracy test of prototype grinder

6 结论

1）针对目前九轴五联动数控缓进给磨床存在的问题，运用ANSYS Workbench 建立了磨床关键零部件及整机的有限元模型，对磨床整机进行动静态特性分析，发现有必要对整机结构进行优化以减小最大静变形；通过模态分析结果得到，该磨床关键零部件及整机的一阶固有频率均大于主轴自转引起的振动频率，但整机的一阶固有频率不算太高，因此有必要在优化结构以减小最大静变形的同时，提升整机一阶固有频率.

2）根据ANSYS Workbench 优化模块及灵敏度分析对磨床关键零部件进行了改进，改进后进行整机装配分析，最大静变形减小28.83%，一阶固有频率提升31.28%.

3）结合前面分析确定的磨床整机优化参数，通过灰色关联分析将三个目标转成综合目标灰色关联度，利用遗传算法优化后的极限学习机网络模型（GA-ELM）拟合磨床结构工艺参数与综合目标灰色关联度之间的非线性耦合关系，再通过遗传算法强大的寻优能力在训练好的GA-ELM 网络模型中极值寻优.通过GA-ELM-GA 优化后的最大静变形一阶固有频率及整机质量得到了优化.最后与工厂初试制产品进行对比分析，验证了进行一切工作的必要性.