生活垃圾料层在机械炉排上的混合与分层现象研究
2022-06-28姜涛王洁华刘海洋张智
姜涛,王洁华†,刘海洋,张智
(1.同济大学机械与能源工程学院,上海 201804;2.上海环境卫生工程设计院有限公司,上海 200232)
随着人们生活水平的不断提高和城镇化进程的不断推进,城市生活垃圾无害化处理需求也在不断提升.采用机械炉排式垃圾焚烧炉对城市生活垃圾进行无害化焚烧发电处理,在达到垃圾减量化目的的同时还能带来额外的发电效益,在行业内得到广泛应用.由于垃圾处理效率对垃圾焚烧发电效益具有重要影响,因此垃圾处理效率提升也成为相关领域内重要研究方向.针对垃圾处理效率提升这一问题,已有的研究主要集中在垃圾料层所处外部环境,如一次风量、二次风量,焚烧温度控制以及垃圾入炉量控制等,而对垃圾料层内部混合分层运动机理的研究还较少.
在可动炉排的周期性往复推动作用下,垃圾料层在整体向炉排尾部前移的同时,内部组分之间也存在混合分层.针对可动炉排运动幅度和往复频率对料层内部分层混合运动机理的影响,已有的相关研究主要从实验或者仿真角度出发.朱新才等设计了一种用于生活垃圾运动研究的炉排实验装置,并在此基础上通过实验对垃圾料层的运动进行实验研究,分析了炉排安装倾角和炉排片行程等参数对垃圾料层运动速度和混合现象的影响[1-3].C.N.Lim 将垃圾料层进行单元划分,提出一种基于概率分析的数学模型来对料层内部颗粒间相互位置交换的概率进行预测[4].离散单元法作为岩土力学研究领域的重要研究方法[5-7],也被一些学者运用于垃圾焚烧领域的研究当中.Harald Kruggel-Emden 等基于离散单元法用不同尺寸的球形颗粒近似替代垃圾颗粒,仿真分析了垃圾颗粒的动态混合过程,并且在不同形式的炉排间进行了对比分析[8].Algis Džiugys 等以离散单元法为仿真手段,以仿真实验为数据来源,通过两种不同的数据分析途径,对比研究分析了垃圾颗粒层在炉排上的停留时间和料层整体的运动速度与可动炉排往复运动的幅度和频率之间的关系[9-12].
以上学者的研究对于揭示垃圾料层内部混合分层现象与可动炉排的运动参数之间的关系具有重要的指导意义,但基本都是基于控制变量法每次只对单一运动参数进行研究.本文基于离散单元分析方法,在参考已有研究的基础上对传统的料层分析方法进行适当改进,构建垃圾料层内部混合分层强度与可动炉排的两个关键运动参数之间的数学关系模型,为机械炉排整体结构参数优化设计提供参考依据.
1 垃圾料层离散化模型构建
由于城市生活垃圾内部成分复杂,理化特性不稳定,现场试验较难开展,研究垃圾料层运动特性的重要途径之一是在对垃圾料层进行适当简化的基础上,采用基于离散单元法的颗粒料层模拟垃圾料层.对于垃圾料层的简化主要有两种方法:采用同一密度不同尺寸的球形颗粒料层[12]和采用同一尺寸不同密度的球形颗粒料层[13].本文采用第一种方法对垃圾料层进行简化,通过创建包含3种不同尺寸颗粒的料层模拟垃圾料层,具体颗粒参数设置如表1所示.
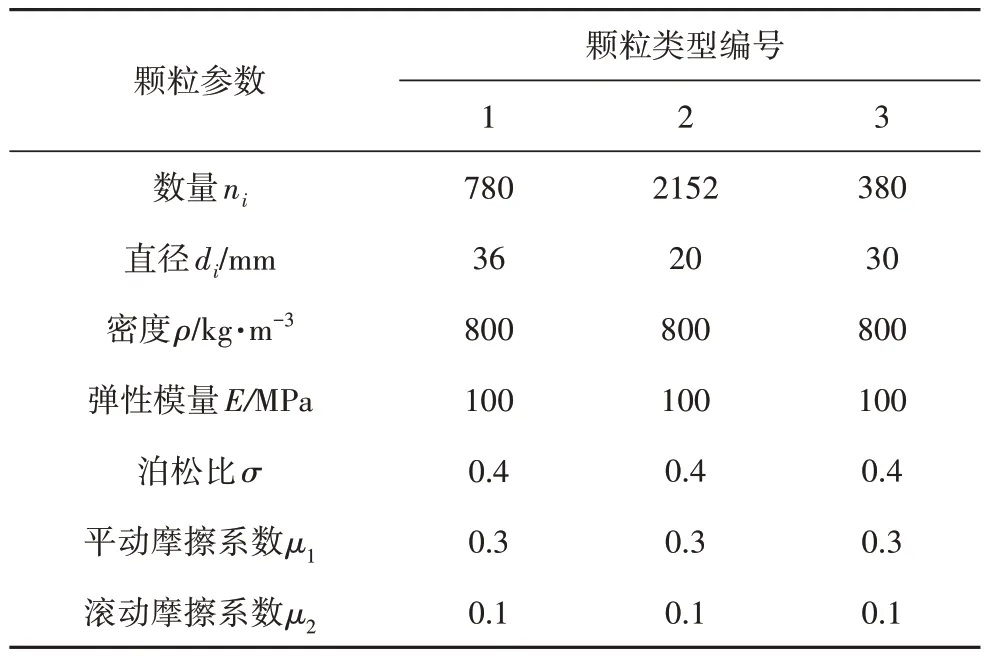
表1 颗粒参数设置Tab.1 Parameters of different particles
通过颗粒工厂对颗粒料层进行初始化设置,让3种颗粒按照表中的数量配置随机分布在炉排模型上方,最终形成如图1 所示的料层初始化模型.在仿真过程中设置x方向和y方向(垂直纸面方向)的周期性边界条件,以此来模拟现实中垃圾料层在炉排上持续性的运动过程,z方向为料层高度方向;模拟现实中炉排倾角设置重力方向与竖直方向夹角为10°.可动炉排片和固定炉排片的尺寸均为长800 mm 高145 mm,可动炉排的往复运动方向如图1 中灰色箭头标注所示,运动形式如公式(1)所示,其中S表示可动炉排位移,A表示运动幅度,f表示运动频率.

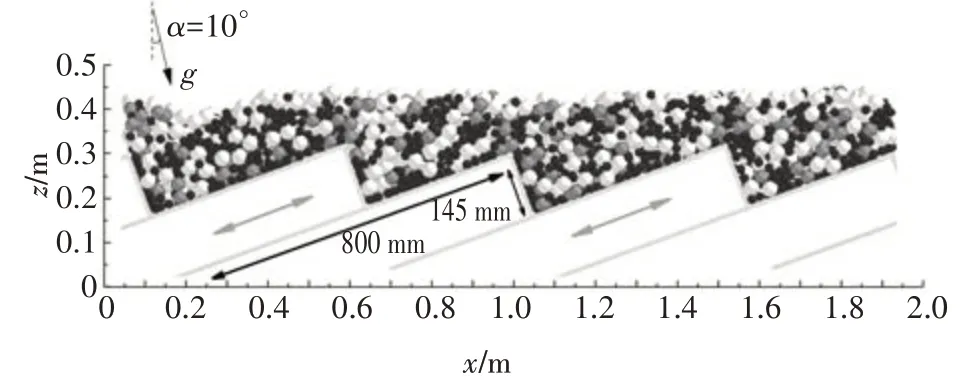
图1 颗粒料层模型初始化配置Fig.1 Initial configuration of the particle layer model
选取可动炉排的运动幅度A和往复频率f作为变量,其中A的取值范围为[0.1 m;0.2 m;0.3 m],f的取值范围为[0.1 Hz;0.125 Hz;0.175 Hz;0.2 Hz].A,f组合共进行12 组仿真实验,仿真时长均为350 s,具体方案如表2所示.
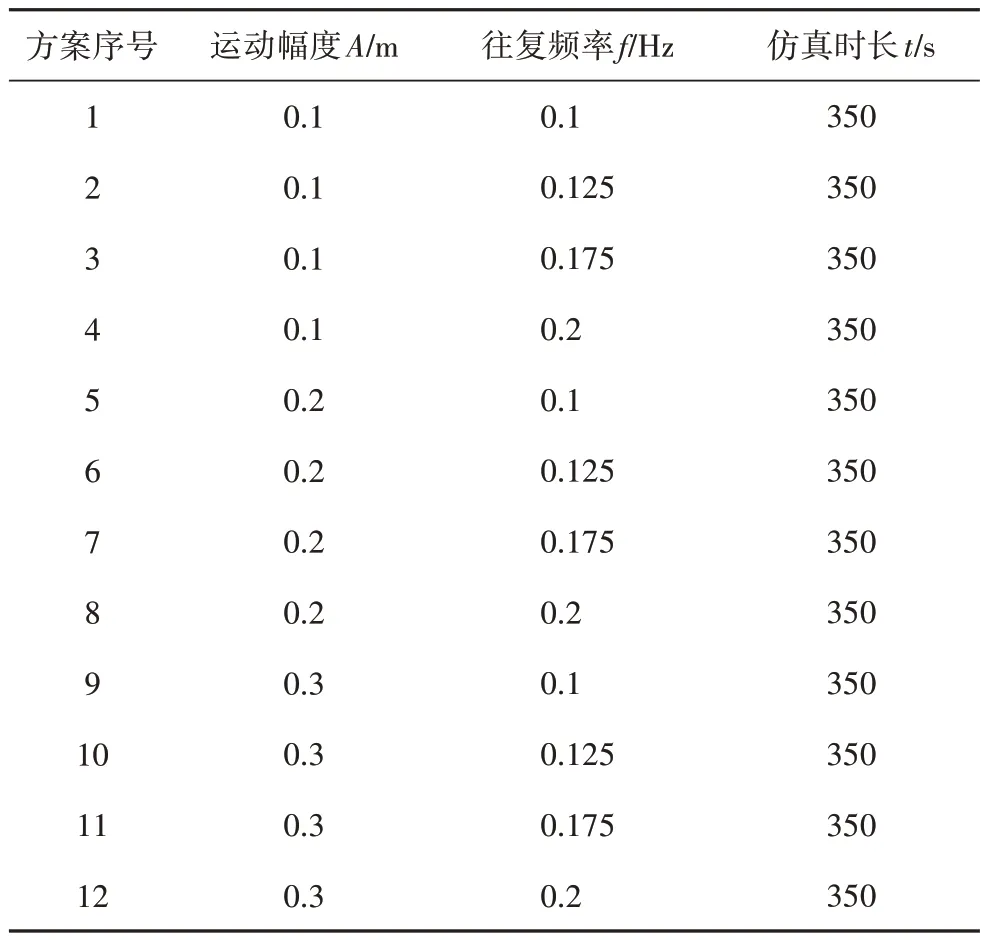
表2 仿真方案Tab.2 Simulation scheme
2 料层混合与分层评价方法
2.1 料层混合分析模型
参考基于颗粒层与流体之间相似性的混合强度分析模型[13-15],将任一颗粒速度vi(t)分解为稳定项V(t)和波动项,如(2)式所示,再通过(3)式用速度波动项来表征颗粒层的内部任意时刻混合强度Mi(t).
模型关键的部分在于V(t)的求解,已有的相关研究对于V(t)的求解是通过计算包含当前颗粒在内的附近区域所有颗粒的局部平均速度来获得,但对附近区域所涉及的范围并未进行严格定义,导致V(t)的值依赖于附近区域的人为定义,缺乏客观性,此外通过局部平均速度构建的分析模型更偏向于反映料层局部混合强度,而无法充分解释料层整体混合强度.考虑到以上V(t)求解方法存在的局限性,为了避免主观因素对求解V(t)的影响,同时使模型能更充分解释料层整体的混合强度,本文通过求解炉排上所有颗粒的全局平均速度来获取V(t).

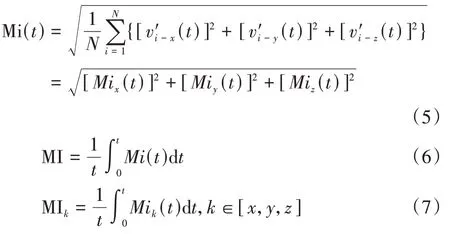
2.2 料层分层分析模型
颗粒料层分层现象研究的一种常用方法是基于不同颗粒层的平均高度求解颗粒料层的分层系数,并以此来表征料层的分层强度[16-18].相关研究方法更多地是针对包含2 种不同尺寸或者密度类型颗粒的颗粒料层.由于垃圾料层组分复杂,3 种颗粒类型相比于2 种颗粒类型能更好地体现垃圾料层组分复杂的特点.在对以上方法进行适当改进后,同样适用于包含3种不同尺寸颗粒类型的情况.
以Hi(t)表示第i种类型颗粒的分层系数,其为关于时间t的函数,求解公式如下.
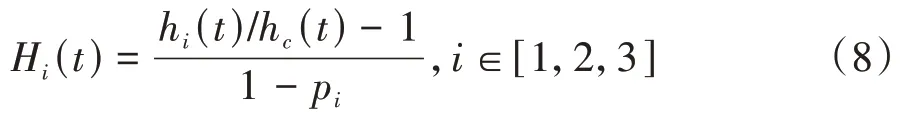
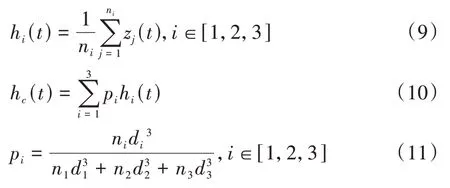
hi(t)表示对应的第i种类型颗粒相对于炉排上表面的平均高度,hc(t)表示整个颗粒料层的平均高度,pi表示第i种类型颗粒在整个颗粒料层中的体积分数(p1+p2+p3=1),ni和di分别表示第i种类型颗粒的数量和直径(见表1).
对于3 种颗粒类型的分层,Hi(t)的理论取值范围在-0.5~0.5 之间.当Hi(t)越接近0.5,表示第i种颗粒的分布区域越靠近料层的顶部;Hi(t)越接近-0.5,则相应颗粒的分布区域越靠近料层底部;Hi(t)越接近0,则相应颗粒分布区域越靠近料层中间区域.
3 仿真试验结果分析
3.1 料层混合
应用以上定义的数学分析方法对仿真实验结果进行分析.图2、图3所示为A=0.3 m,f=0.2 Hz时对应的颗粒料层在x、y、z三个方向的瞬时混合系数Mix(t)、Miy(t)和Miz(t)在整个仿真时长350 s 内以及前50s内随时间变化的曲线图.

图2 整个仿真周期内颗粒料层混合系数随时间变化曲线Fig.2 Evolution curve of the particle layer′s mixing index over the entire simulation period
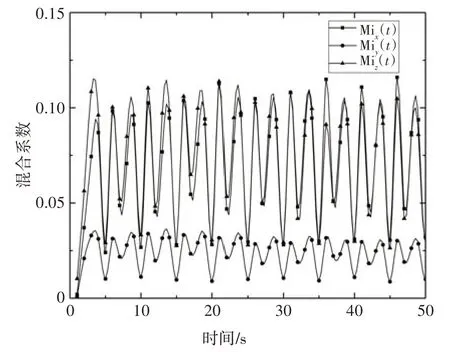
图3 0~50 s期间颗粒料层混合系数随时间变化曲线Fig.3 Evolution curve of the particle layer′s mixing index over 0-50 s
从图中可以看出,Mix(t)和Miz(t)重叠区域较多,且均处于Miy(t)的上方,表明颗粒料层在沿着炉排的x方向(料层推进方向)和z方向(料层高度方向)的混合强度基本一致,且均大于y方向的混合强度.由于可动炉排的推动作用使得料层的运动主要集中在x和z方向,因此料层内部组分的混合也主要发生在对应的两个方向.
通过(5)(6)式对料层三个方向的瞬时混合系数进行积分运算,得到颗粒料层在整个仿真时长内的混合系数MI,以此表征料层在整个仿真时长内的混合强度,计算结果如表3 所示.图4 为分别以MI 为z轴,A为x轴,f为y轴得到的散点图,通过散点图可以发现,MI 与A和f之间存在非常明显的线性相关关系,因此对三个变量进行多元线性拟合分析,拟合函数如下:
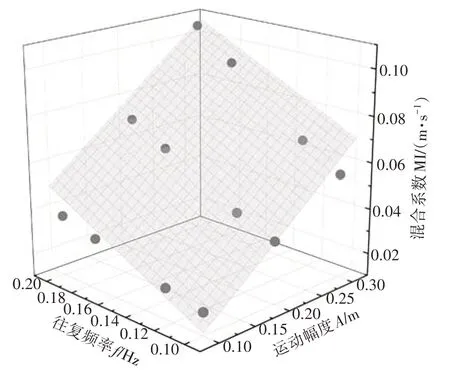
图4 MI散点图和二元线性拟合平面Fig.4 Scatter plot of mixing index and the corresponding bivariate linear fitting plane


表3 不同仿真条件对应的混合系数值Tab.3 Values of mixing index corresponding to different simulation conditions
通过表3中的12组数据进行拟合分析得到拟合结果如表4所示.其中R2=0.9540,接近于1,表明模型的拟合优度非常高;在给定显著性水平α=0.05 条件下,查F分布表得到临界值Fα(2,9)=4.256,F>Fα(2,9),表明MI 与A和f之间的线性相关关系在95%的水平下显著成立.将拟合结果代入(12)式得:
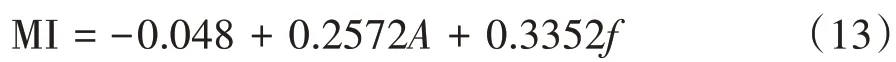

表4 二元线性拟合结果Tab.4 Result of bivariate linear fit
公式(13)将料层的整体混合系数和可动炉排的运动幅度以及往复频率直接关联,揭示了炉排上的料层内部组分间的混合强度与可动炉排相关运行参数之间的关系.
3.2 料层分层
图5为A=0.3 m,f=0.2 Hz时3种类型颗粒在料层高度方向的分层系数H1(t)、H2(t)和H3(t)在整个仿真时长350 s 内随时间变化的曲线图.图6 所示为料层在0 s、50 s、100 s、150 s、200 s、250 s、300 s、350 s 时刻的分层状态,其中白色颗粒为颗粒1(颗粒直径为36 mm),黑色颗粒为颗粒2(颗粒直径为20 mm),灰色颗粒为颗粒3(颗粒直径为30 mm).
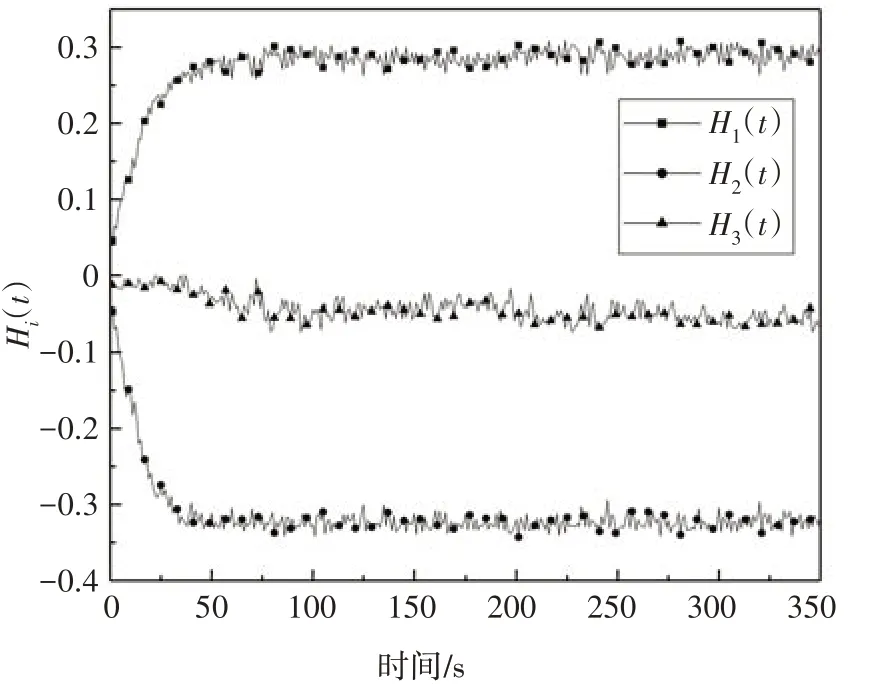
图5 整个仿真周期内颗粒料层分层系数随时间变化曲线Fig.5 Evolution curve of the particle layer′s segregation index over the entire simulation period
从图中可以看出随着时间变化,料层整体逐渐出现分层,并最终产生稳定的分层现象.根据仿真实验初始配置,初始时刻3 种不同尺寸类型颗粒在料层中随机分布并未开始出现分层现象[图6(a)],因此分层系数均接近零值.随着可动炉排的不断往复推动,三种颗粒之间开始出现明显的分层,大约经过50 s 左右H1(t)、H2(t)和H3(t)达到稳定值0.3、-0.32和-0.05.其中H1(t)稳定值约为0.3,表明颗粒1 在经过分层后集中分布在靠近料层顶部区域[图6(b)]所示白色颗粒区域);H2(t)稳定值约为-0.32,表明颗粒2 在经过分层后集中分布在靠近料层底部区域[图6(b)]所示黑色颗粒区域);H3(t)稳定值约为-0.05,表明颗粒3在经过分层后集中分布在料层中间区域(图6-(b)所示灰色颗粒区域).上述分层现象可以通过巴西果效应(Brazil nut effect)来解释,该效应指出,在粒状料层被施加外部振动时,大尺寸颗粒会趋向分布于料层顶部,小尺寸颗粒则趋向分布于料层底部,这也与仿真实验结果相符合.
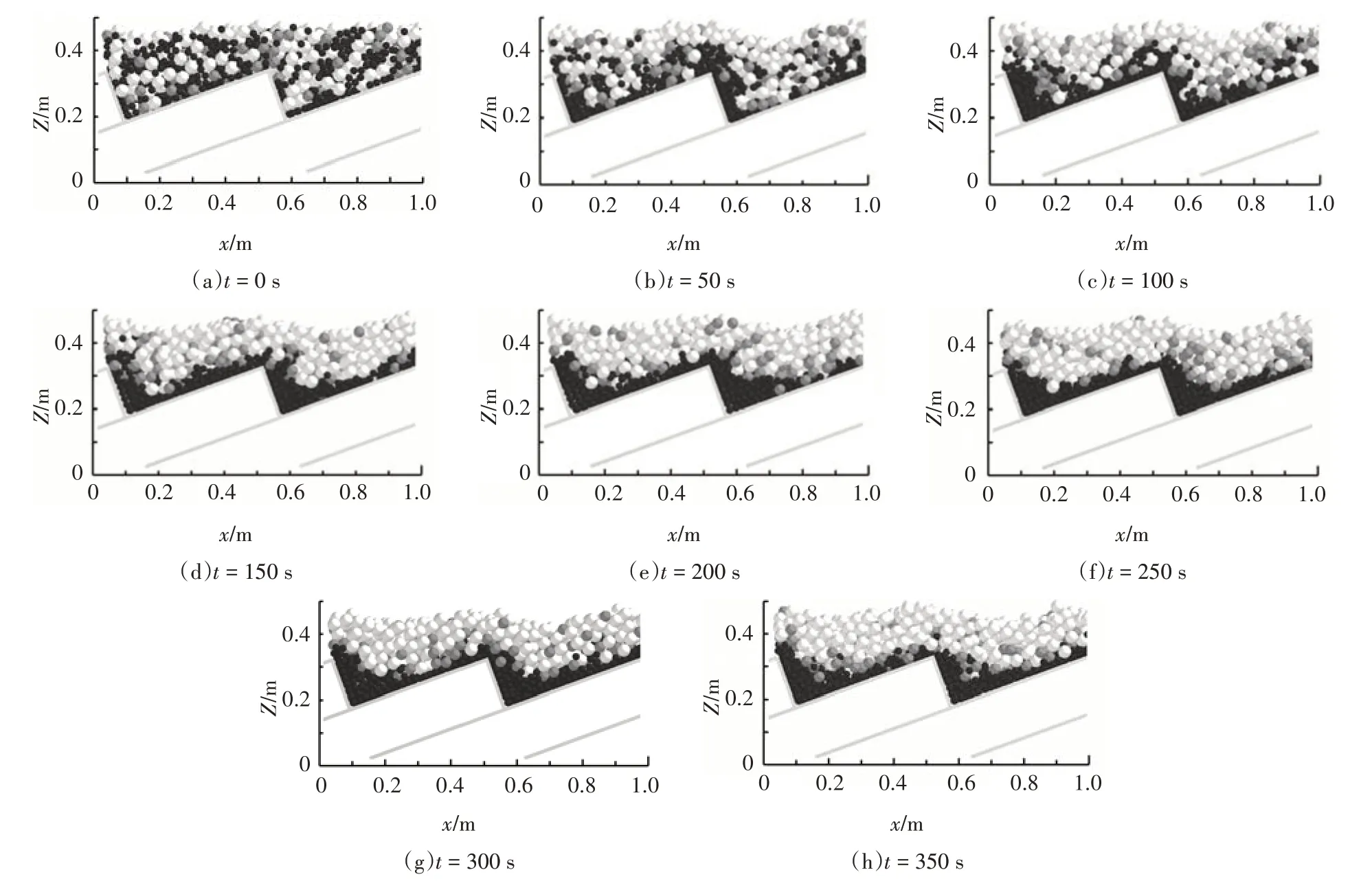
图6 料层分层状态随时间变化过程Fig.6 Segregating process of particle layer over the entire simulation period
通过上述分析可知,在可动炉排的往复推动作用下,料层内部不同组分间会发生分层现象,其中较大尺寸颗粒会朝着料层顶部集中,较小尺寸颗粒朝着料层底部聚集,中等尺寸颗粒则主要分布在料层中间区域.此外,随着时间推移,分层现象会越来越明显,3种类型颗粒对应的分层系数最终会达到一个稳定值.
进一步研究分层现象完成的速度(即分层系数达到稳定值的快慢程度)与可动炉排运动幅度和往复频率间的关系.根据以上分析,当t→∞,Hi(t)→常数时,结合分层系数曲线变化趋势提出式(14)所示经验公式对Hi(t)进行拟合,其中c0表示Hi(t)的稳定值,c1为调整系数,τ为时间常数,其大小与Hi(t)变化快慢直接相关,τ越大Hi(t)越快达到稳定,因此以τ表征料层分层快慢.拟合曲线如图7 所示,拟合结果能够准确地预测Hi(t)的变化趋势.此处只展示A=0.3m,f=0.2Hz 时的拟合结果,其他仿真组的最终拟和结果在表5中列出.

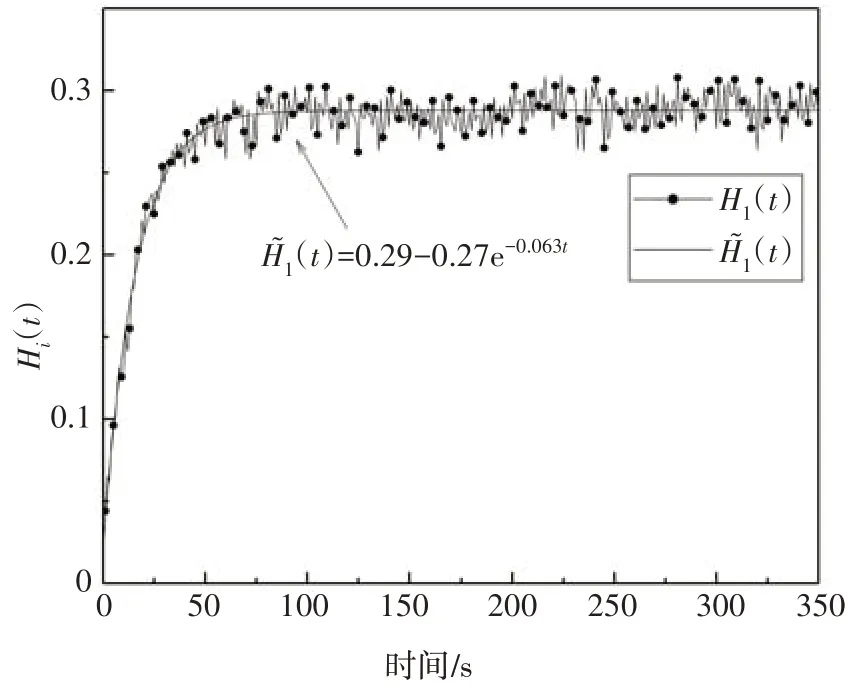
图7 颗粒料层分层系数随时间变化趋势拟合Fig.7 Nonlinear fitting of segregation index evolution trend
图8 为以时间常数τ为z轴、A为x轴、f为y轴得到的散点图.如散点图所示,当f(或者A)保持不变,τ与A(或者f)之间存在线性相关关系,且随着f(或者A)增大,斜率也越大.基于以上特征,提出公式(15)所示拟合函数对三个变量进行多元非线性拟合分析:


图8 时间常数τ散点图和二元非线性拟合平面Fig.8 Scatter plot of time constant and the corresponding bivariate nonlinear fitting plane
通过表5中的12组数据进行拟合分析得到拟合结果如表6 所示.其中R2=0.9879,接近1,表明模型的拟合优度非常高,能够很好地解释τ与A和f之间的关系;均方差MSE(模型的预测值与实际值之间误差的平和均值)为3.092e-06,接近0,表明模型预测值和实际值之间误差很小.将拟合结果代入(15)式得:

表5 分层系数变化趋势拟合结果Tab.5 Fitting result of segregation index evolution trend
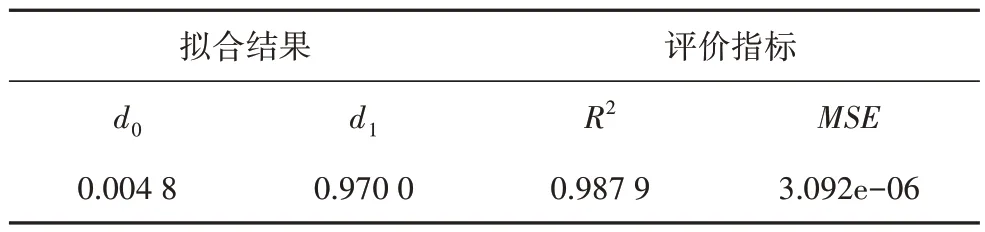
表6 二元非线性拟合结果Tab.6 Result of bivariate nonlinear fit
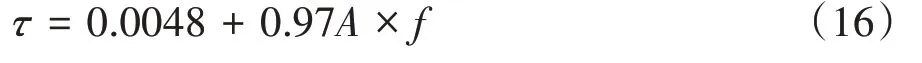
公式(16)建立起料层内部分层速度和可动炉排的运动幅度以及往复频率之间的数学关系,通过控制可动炉排的相关运行参数可以达到调节垃圾料层分层时间的目的,对于解释垃圾料层内部分层现象具有一定参考价值.
4 结论
基于离散单元法的仿真实验方法,建立了包含3种不同尺寸类型颗粒的颗粒料层模拟垃圾料层,在引入颗粒料层混合和分层数学分析模型的基础上,通过12 组仿真实验对料层内部的混合和分层现象分别进行研究,得到以下主要结论:
1)可动炉排的往复运动导致垃圾料层内部组分之间的混合主要发生在沿着炉排的料层推进方向和料层高度方向;
2)垃圾料层内部组分之间的混合强度MI与可动炉排运动幅度A和往复频率f之间存在非常明显的二元线性相关关系;
3)可动炉排的往复运动会导致垃圾料层内部不同尺寸组分相互分层,其中较大尺寸组分会朝着料层顶部集中,较小尺寸组分朝着料层底部聚集,中等尺寸组分则主要分布在料层中间区域;
4)表征垃圾料层内部分层快慢程度的时间常数τ与可动炉排运动幅度A和往复频率f之间存在二元非线性相关关系.
通过定量化分析料层内部组分运动机理,为解释垃圾料层内部混合与分层现象提供参考依据.在此基础上分析了可动炉排的工艺参数运动幅度和往复频率,对垃圾料层内部混合和分层的影响,为机械炉排的优化提供参考.
