发散光束对消光法颗粒粒径测量影响

肖新宇，熊兵，陈军，杨荟楠，苏明旭

（1 上海理工大学能源与动力工程学院，上海市动力工程多相流动与传热重点实验室，上海 200093）

（2 中国航发四川燃气涡轮研究院，成都 610500）

0 引言

在颗粒测量方法［1-3］中消光法测量原理简单、操作简便，易实现仪器设备微型化，如利用光纤和光谱仪即可测得携带粒径信息的消光谱并反演颗粒粒径分布［4-5］。消光法的理论基础为Lambert-Beer（LB）定律和Mie 散射理论，前者反映了光束在介质中的透射和衰减特性，后者描述单个均质球形颗粒的光散射规律。通过测量离散状态颗粒系的消光谱再结合Mie 理论构建消光系数矩阵，可反演出颗粒粒径分布［6-7］。该方法通常基于平行入射光条件，但在一些特定应用场景中入射光束并非严格平行，例如高斯光束照射或某些发光二极管（Light Emitting Diode，LED）光源条件。此外，测量空间狭小时往往采用光纤传递发射和接收信号，因其具有一定的发散和接收角，按平行入射光假设处理会导致误差。

关于非平行光束消光和光散射问题，刘福水等［8］搭建一套非平行光二维测试系统准确获得扩散火焰中的碳烟浓度分布，解决了平行光消光法在碳烟测试中的波束偏移问题。冯冰等［9］利用蒙特卡罗方法［10-12］（Monte Carlo Method，MCM）模拟大气气溶胶对高斯光束的侧向散射，获得侧向散射光强和散射系数曲线并与实验结果对比验证。周田华等［13］基于蒙特卡罗仿真分析光束发散参数对接收光场分布的影响，通过光束预聚焦处理一定程度上抵消水体传输引起的光束扩散，增强了接收光信号功率。CHEN J 等［14］基于Mie理论推导了发散光束入射下探测面上散射光空间分布的解析表达式，通过不同发散角模拟和实验的散射光强分布曲线验证了其适用于不同发散角下小粒径测量。WANG Z 等［15］基于蒙特卡罗偏振辐射传输模型，研究了激光束发散对来自均匀平面平行水云的激光雷达多次散射偏振信号的影响。VALI Z 等［16］基于蒙特卡罗模型，研究平面光束、高斯光束和球面光束的发散度对清澈水域链路对中的影响，发现提高发射器波束发散度可以减小发射和接收器未对中的影响，并且存在一个最佳发散角可平衡横向偏移、功率损耗和信号带宽之间关系。LI M 等［17］设计一种基于梯度散射的光纤扩散器，利用蒙特卡罗方法模拟了不同的非对称因子和光纤发射角下光纤扩散器在水和空气中的发射性能。NICO S 等［18］基于统计消光法在线测量颗粒通过光束运动产生的光强波动，根据统计的波动信号计算出颗粒平均粒径和颗粒浓度，并设计一种空间频率滤波器有效减小了颗粒多次散射对信号测量的影响。

不过，上述研究均未涉及多波长条件的消光法测量问题，消光法由于借助了不同波长下消光谱信息，而非散射光的空间分布信息，其特点和前述研究不同。为此，作者借助蒙特卡罗方法和标准颗粒的测量从数值和实验角度研究发散光束对消光法颗粒粒径测量的影响。

1 测量方法

1.1 消光法原理

如图1 所示，一束直径远大于被测颗粒粒径，强度为I0，波长为λ的平行单色光入射到一含有测颗粒群的介质时，由于颗粒对光的散射和吸收，透射光I的强度为

图1 消光法测量原理示意Fig.1 Schematic of light extinction measurement

式中，τ是介质浊度，L为光程。对于球形被测颗粒，且各颗粒光散射满足不相关单散射，单位体积内N个粒径为D的单分散颗粒系浊度τ为

式中，Cext和kext分别为消光截面和消光系数，是入射光波长λ、被测颗粒粒径D、颗粒相对于介质的相对折射率m的函数。将式（2）代入式（1）可得

理论上，通过LB 定律建立正演模型并计算消光系数矩阵，对所测消光谱反演可得颗粒粒径分布信息。不过，该模型的适用前提需满足平行光入射条件，而实际测量如采用非平行入射光源，仍依照LB 模型会带来一定误差。对于发散光入射情形，引入蒙特卡罗方法，将入射光束离散化处理成离散光子，通过统计不同方位接收器接收到的光子数即可模拟不同发散角范围下的消光特性，进而分析对消光谱和粒径反演的误差。

1.2 蒙特卡罗仿真流程

蒙特卡罗方法是以概率统计为基础的随机模拟方法，将光在颗粒离散介质中的散射过程视为光子与颗粒的碰撞过程，且每次散射只与前一次散射有关［19］。通过跟踪大量的光子轨迹模拟光在散射介质中传播的整个物理过程，统计出各个方位接收器接收到的光子数，并可获得边界逃逸、前向透射、散射的光子数。

图2 为模拟发散光束穿过散射介质的传播模型，散射介质厚度为L，介质到发射和接收器距离都为S。假设光束在z=0 平面沿着z轴方向传播，发散角为θ。光子的初始出射坐标(x0，y0，z0)为（0，0，0），初始出射方向余弦(ux0，uy0，uz0)表示为

图2 发散光束仿真模型Fig.2 Simulation model of the divergent beam

式中，θ0和φ0为发散光子的初始散射角和方位角，光子在初始发散角范围内均匀分布。结合初始方向余弦可计算得光子刚进入测量区坐标为，并以此坐标作为起算坐标。光子与颗粒碰撞相邻的两次散射之间的随机自由步长可表示为

式中，rl是［0，1］范围内均匀分布随机数，消光效率Kext可由Mie 散射理论计算。 结合起算坐标、初始方向余弦以及相邻散射间的随机自由步长，光子首次发生散射的坐标(x1，y1，z1)可以表示为

光子与颗粒碰撞后的空间散射角分布可以由Henyey-Greenstein 相函数［20］确定，对相函数抽样，散射角θ1的抽样表示为

式中，rθ1是另一个［0，1］范围内随机数，g是不对称因子。再结合初始方向余弦以及发生散射后的散射角、方位角得到新的方向余弦为

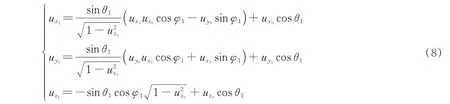
据此，由每一次散射后的方向余弦以及随机自由步长可以确定每次光子与颗粒碰撞的坐标，直至判定光子是否被吸收、从边界逃逸还是被接收。依据反照率a（a=Csca/Cext，散射截面与消光截面的比值）判定光子是否被吸收，当随机数rα≥a时光子被吸收，反之被散射。假设接收器直径为d，接收角为ψ，当光子z轴方向坐标zi≥2S+L，停止对光子跟踪并修正坐标得zi=2S+L，此时判定光子被接收的条件为

记录接收光子数目n，并重复下一个光子历程，直到完成所有光子计算，统计各个物理过程的光子数得到散射介质的消光特性。消光谱可表示为

式中，n为接收光子总数，nset为设定光子数。

2 数值模拟

2.1 光子去向统计

按照前述模型编制计算程序，通过统计每个物理过程的光子数可得颗粒系的散射和吸收特性。算例选取颗粒粒径D=0.2 μm、相对折射率m=1.196、体积浓度Cv=4×10-5、介质厚度L=10 mm，接收器尺寸d=0.8 mm。光子在散射介质中传输过程的分类如图3，可以看出在给定粒径下，随着波长增大透射光子数逐渐增多。按光散射理论，波长增大时亚微米区颗粒的无因次参数α（α=πd/λ）减小，消光系数减小，再结合蒙特卡罗方法计算随机自由步长的公式分析，波长增大导致随机步长增大，光子准直透射的概率增加。无因次参数减小，光子与颗粒碰撞后的角散射特性趋于均匀，图中前后向散射的光子数逐步接近。同时，光子准直透射的概率增大，发生散射、吸收以及边界逃逸的光子数逐渐减小。

图3 光子去向统计Fig.3 Statistics of photon events

2.2 程序验证

为验证蒙特卡罗计算程序的正确性，设定光子准直出射（发散角为零），将蒙特卡罗方法计算的准直透射光消光谱与LB 模型预测对比验证，并由图4 给出在不同粒径下消光谱ln(I0/I)随波长λ的变化规律。算例选取粒径D为0.2、2.88 μm、m=1.196、Cv=4×10-5、L=10 mm，为减小复散射对计算结果影响，粒径0.8 μm 时选取体积浓度Cv=2×10-5。由图中曲线可以看出蒙特卡罗和LB 模型计算结果吻合较好，其在不同的粒径下消光曲线的变化趋势均非常接近。综合考虑计算效率以及计算结果稳定性，数值计算光子数选取105。

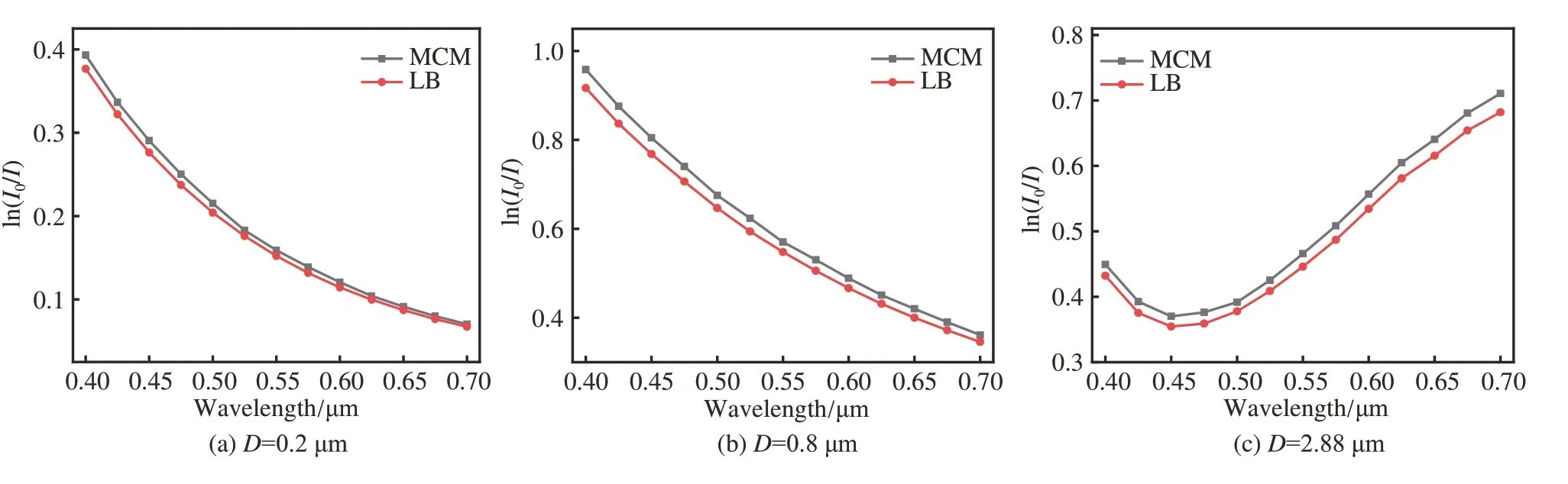
图4 蒙特卡罗和LB 模型消光谱对比Fig.4 Comparison of extinction spectra of Monte Carlo and LB models

2.3 不同接收器尺寸和接收角消光谱

图5（a）为粒径D=0.8 μm、接收角ψ=25°、光子准直入射时，不同接收器尺寸下消光谱ln(I0/I)随波长λ的变化规律。从图中不同接收器尺寸下的消光谱曲线可以发现，接收器尺寸越大对应消光值越小，这是由于大尺寸接收器接收的透射和散射光能越多所致。图5（b）为不同接收角下消光谱ln(I0/I)随波长λ的变化规律，在光子准直入射情况下，接收角度从10°～30°变化对于消光谱的影响较小。

图5 不同接收器尺寸和接收角消光谱对比Fig.5 Comparison of extinction spectra with different receiver sizes and different reception angles

2.4 不同发散角范围消光谱

图6 是接收器尺寸d=0.8 mm、接收角ψ=25°，三种粒径颗粒不同发散角下消光谱ln(I0/I)随波长λ的变化规律。从图6（b）、（c）可以看出消光值随发散角递增，因发散角增大使得光子发生散射后穿过介质时愈加偏离接收器中心，导致接收器接收到的散射光能更少。同理，发散角增大光子在与颗粒碰撞发生越界的概率越大，也会导致消光作用增强。再通过与图6（a）对比发现，粒径D=0.2 μm 时发散角增大消光值会略微增大但是曲线无明显差异，经分析可知该粒径下透射光子占主导，发散角的变化所导致接收的散射光能变化对于总接收光能的影响甚微。从单颗粒光散射特性可知此粒径下颗粒的无因次参量α很小，光子与颗粒碰撞后散射呈均匀分布，相较于大粒径颗粒前向接收散射光能占比更小。模拟选取接收尺寸为0.8 mm，如接收尺寸增大，则发散角的变化对消光曲线的影响应更明显。

图6 不同发散角范围的消光谱对比Fig.6 Comparison of extinction spectra at different divergence angles

3 实验与结果

3.1 实验系统

实验系统如图7，实验采用波长范围为0.4～0.7 μm，输出功率为0～1 mW 可线性调节的LED 光源，如海光电科技生产的SEED3000 型光谱仪（可测光谱范围为0.341～1.064 μm，波长数目为2 048），多模发射和接收光纤直径为0.8 mm，发射和接收角均为25°，发射和接收光纤的距离Z=100 mm。LED 光源发出具有一定发散角（60°）的白光光束，发散光束通过焦距为25 mm、孔径为25.4 mm 的傅里叶光学透镜汇聚成平行准直光束，照射在光程L=10 mm 的四通光样品池上。样品池置于发射、接收光纤之间，控制光束完全照射到样品池壁面，经过颗粒的散射吸收发生衰减后，携带颗粒粒径信息的光能被光纤接收并传递至光谱仪，将10 次连续采集的实验数据取平均后计算消光谱。为测得发散光束消光谱，首先通过调节透镜与光源距离使光束汇聚，控制第一个光阑孔径取光束最均匀部分，再调节第二个光阑孔径（可调节范围为1.5～30 mm），根据两个光阑间距和孔径限定其发散角分别为5°、10°、15°、20°，进行实验。

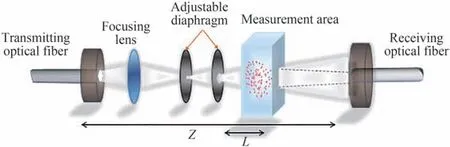
图7 消光实验系统示意图Fig.7 Schematic of light extinction experiment system

3.2 消光谱和颗粒粒径分布反演

实验用标准颗粒为中国石油大学研制标称直径分别为0.2、0.8、2.88 μm 的三种聚苯乙烯乳胶微球。分别测得每种颗粒在平行光及不同发散角入射条件下的透射光能，经处理得如图8 所示的消光谱曲线。对于粒径D=0.2 μm 颗粒，发散角变化对消光谱影响不明显，但是对D=0.8 μm 和D=2.88 μm 的颗粒，随着发散角增大消光谱有明显的变化，其变化趋势和数值模拟结果基本一致。消光法LB 模型中透射光是指理论准直出射光束（未发生散射），但由于实际光程所限部分前向小角散射光也会被接收，这与单颗粒散射特性相关并和光波长、颗粒粒径及入射光角度等参数关联，进而对获取的消光值大小与光谱曲线产生影响。

图8 实验测得不同发散角下的消光谱Fig.8 The experimental extinction spectra at different divergence angles

在400～700 nm 波长范围内等间距的选取50 个波长的消光谱，采用DFP（Davidon-Fletcher-Powell）算法［21-22］反演得到粒径分布结果。如图9 所示，对0.2 μm 颗粒，发散角变化对反演结果影响不明显，粒径分布曲线较为稳定，对粒径0.8、2.88 μm 颗粒，随着发散角增加反演结果误差越大，粒径分布曲线整体发生偏移。

图9 不同发散角下反演颗粒粒径分布Fig.9 Inversed particle size distributions at different divergence angles

3.3 颗粒粒径误差

图10 为不同发散角下，由数值模拟和实验消光谱反演的索太尔（Sauter）平均直径与标称值的误差。从图中可以看到平行光入射时，反演结果误差较小，随发散角增大模拟和实验消光谱的反演结果与标称值误差整体增加。发散角在5°范围内三种粒径的反演结果误差均在4.62%以内，但发散角增至20°时，对于粒径为0.8 μm 的颗粒模拟和实验反演结果误差达10.29%和12.75%；对于粒径为2.88 μm 的颗粒模拟和实验反演结果误差达-7.64%和-9.55%，此时发散光束将严重影响测量结果。

图10 不同发散角下模拟和实验平均粒径结果误差Fig.10 Errors of mean sizes at different divergence angles in simulations and experiments

3.4 颗粒粒径反演修正

为修正发散光束对消光法粒径测量结果的影响，在粒径0.05～5 μm、入射光波长0.4～0.7 μm 区间各线性分50 档，用蒙特卡罗程序计算不同发散角下的消光值并构建系数矩阵代替Mie 理论计算的消光系数矩阵，代入反演算法。对粒径0.8 μm 的颗粒在发散角为5°、10°、15°、20°下实验消光谱反演，修正前后反演结果与误差如表1。可见经修正后，不同发散角下粒径的反演结果误差在2.00%内，表明该方法可减小入射光束发散对测量结果造成的误差。

表1 修正前后不同发散角下颗粒反演结果和误差（D=0.8 μm）Table 1 Inversed results and errors at different divergence angles before and after correction（D=0.8 μm）

4 结论

采用蒙特卡罗方法模拟发散光束下发散角变化对消光法粒径测量的影响，搭建基于发散光束的消光法实验平台，针对三种不同粒径的聚苯乙烯乳胶球标准颗粒进行实验，测得不同发散角条件下的消光谱，并反演出颗粒粒径分布。结果表明：不同发散角下实验消光谱的变化趋势与数值模拟结果基本一致；颗粒粒径反演误差整体上随发散角增大而增加，在20°发散角下粒径为0.2、0.8、2.88 μm 的颗粒测量结果误差分别为4.25%、12.75%、-9.55%。对粒径0.8 μm 的颗粒在发散角为5°、10°、15°、20°的实验消光谱反演修正，反演误差在2.00%以内，该方法可实现对于此类问题的误差修正。