基于光学三角法的芯片凸点高度测量
2022-06-28王棚孟繁昌张滋黎王德钊王珊姚恩涛王磊叶瑞乾
王棚,孟繁昌,张滋黎,王德钊,3,王珊,姚恩涛,王磊,叶瑞乾
(1 南京航空航天大学自动化学院,南京 211100)
(2 中国科学院微电子研究所,北京 100029)
(3 长春理工大学,长春 130022)
(4 厦门大学,福建厦门 361101)
0 引言
摩尔定律为集成电路行业的发展提供了理论指导,未来通过封装和微系统扩展实现的异构集成将进一步补充摩尔定律。当前的2D 和3D 封装结构是实现异构集成最理想的技术形式。2D 封装结构是指形成互联的两个或多个有源器件以横向方式并排放置的封装结构;而3D 封装则将这些有源器件以纵向方式堆叠放置。2D 封装结构和3D 封装结构中采用的互联技术主要包括引线键合(wire-bounding)和凸点键合(bump- bounding)。其中,凸点键合技术采用导电凸点结构实现芯片对芯片(die-to-die)、芯片对基板(dieto-wafer)之间的电气互联互通。同时,凸点还可以作为器件之间的支撑结构[1]。如果凸点互联结构存在缺陷乃至失效将导致封装芯片的良率下降,因此需要在凸点制备过程中对其进行在线测量。凸点互联失效模式主要包括错位、缺失、桥接以及高度不一致[2]。传统二维测量方法只能检测凸点错位、缺失和桥接,不能实现凸点高度一致性的测量。此外,随着芯片集成度的进一步提高和凸点键合技术的发展,凸点高度也随之压缩。现存的先进封装技术中,常采用的凸点结构包括焊料凸点(100 μm)和微凸点(<25 μm)[3],对于这类小微凸点的高度一致性快速在线测量需求日益迫切,且对于测量精度的要求越来越高,在工业现场对于测量精度的要求逐渐由微米级提升到亚微米级。
针对芯片凸点高度的测量,传统的测量方法包括光谱共聚焦法[4-6]、白光干涉法[7-8]、投影光栅法[9-10]、光学阴影法[11]和光学三角法等[12-15]。光谱共聚焦法分辨率高,对复杂表面的测量没有光学伪影,可以实现优于0.1 μm 的测量精度,但测量速度较慢。白光干涉法测量精度可以达到纳米级,但测量范围较小,同样存在测量速度慢的问题。投影光栅法单次测量面积大,测量速度较快,但测量精度受限于投影设备分辨率和相位提取算法,只能达到微米量级;高频超声波法可以检测多层结构中各部分的高度,但需要预先知道各层材料中的声速。光学阴影法测量速度较快,但测量精度在微米以上量级,且测量结果易受凸点间距和入射光线角度的影响。光学三角法相比于以上方法的优势在于原理简单、实验设备成本低且测量速度快、可以实现芯片封装缺陷在线测量的需求[16]。MANUEL F M 等设计了一种基于光学三角法的高度测量装置,将入射光束聚焦在待测物体表面上形成亮斑,通过逐点扫描实现对物体表面形貌的检测,其横向分辨率为1 μm,纵向分辨率可达2 nm。该装置多用于粗糙度和残余应力的测量,但测量系统量程相对较小、由于是利用点扫描测量,速度相对较慢[17];文献[18]中,三角测量传感器投射两束不同波长共光路的线光束到被测物体上,相机采集经物体表面形貌调制后的光条信息,解析得到物体表面不同位置的高度信息,该装置的测量标准偏差为3.41 μm,相比于点光源,该装置采用线光源,能够提升测量速度,但测量精度不能满足凸点检测的需求。
针对以上光学三角测量系统存在的问题,本文针对芯片凸点形貌特征,提出了一种基于光学三角法的芯片凸点高度测量方法。该方法将白光LED 发出的光线经过整形后形成线结构光投射到凸点上,凸点顶部和芯片基板上的反射光线经过透镜后投射在相机靶面上,根据图像中的几何特征信息,结合凸点高度测量的数学模型,可以实现凸点高度的亚微米级精度测量,测量精度相对于传统光学三角法有较大提升,同时采用线结构光代替点光源进行测量,可使测量速度显著提升。
1 芯片凸点高度测量模型
按照入射光线与被测物体表面的位置关系,光学三角法可以分为直射式与斜射式。直射式的图像传感器(CCD/CMOS)适用于测量表面粗糙度较大的被测物;斜射式的图像传感器能够接收反射光,可用于表面粗糙度较低物体的测量[19-21]。图1 所示为待测样品在电子显微镜下观察到的三维形貌。该芯片上的凸点形状为球形,且为锡银材质。锡球表面光滑,光线在其表面发生镜面反射,因此实验中采用斜射式光学三角法测量凸点高度。

图1 扫描电子显微镜下芯片凸点的结构Fig.1 Structure of chip bump under scanning electron microscope
图2 所示为斜入射光学三角法原理图,图中虚线为光源投射的光条边缘,实线为光条中心线。因为光条具有一定的宽度和长度,反射光经过透镜后汇聚在相机靶面上形成矩形光条。当改变参考平面的高度时,图像中光条中心的位置将发生改变。在ΔABD中,AB=AD/cosθ=y/cosθ,式中,y为被测物体表面的高度差,在ΔABC中,AB=AC/sin 2θ=d/(β·sin 2θ),式中,β为成像系统放大倍率。参考平面高度差y与图像中光条中心的位移d之间的线性关系表示为

图2 斜入射光学三角原理图Fig.2 Schematic diagram of oblique incidence optical triangulation
式(1)可以写为y=kd,式中k=1/(2βsinθ),β为成像系统放大倍率,θ为入射光线与物平面法线的夹角。根据式(1)可以利用图像中不同光条之间的偏移值计算出不同平面间的高度差。
当被测对象的上下表面均为平面时,上述测量公式适用。但当被测对象为芯片凸点时,当光束宽度可以忽略时,光投射到凸点顶部和底部后的反射光满足式(1)。但在实际情况中,受到光条宽度的影响,矩形光束投射到凸点及底板上时,被底板反射后的光束在物镜像平面探测器上形成长条形光斑。由于凸点上部分形状为球体,使得像平面上的长条形光斑出现圆弧形缺口,如图3(b)所示。当光条投射到凸点顶部不同位置时,圆弧形缺口随光条位置的变化而变化。只有在光条中心位置投射到凸点顶部时,凸点高度公式才能用公式(1)解算,但实际测量过程很难保证这一条件。针对此问题,本文提出了一种不受光条位置和宽度影响的凸点高度测量数学模型。
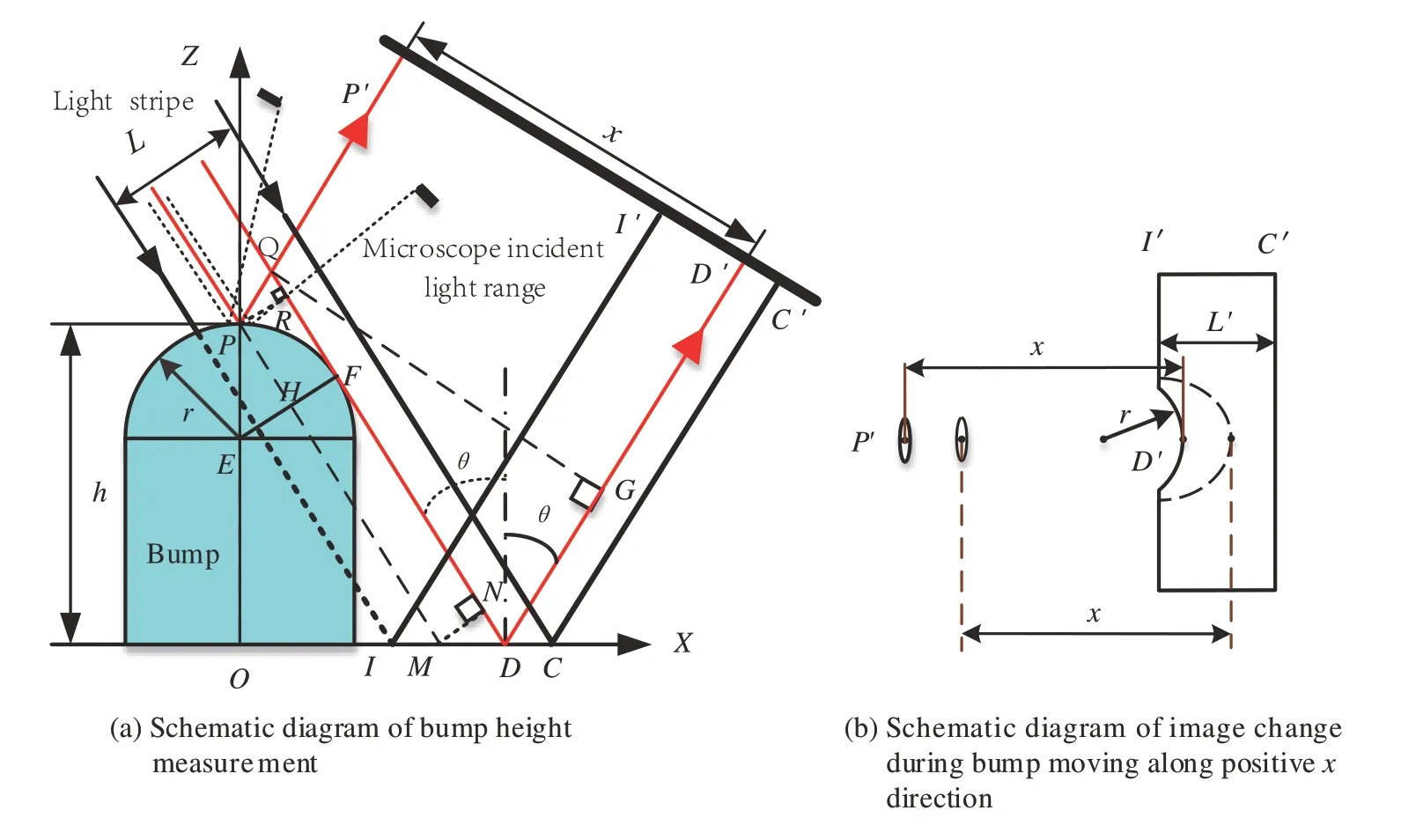
图3 芯片凸点高度数学模型原理图Fig.3 Schematic diagram of chip bump height mathematical model
如图3 所示,在XZ平面内,宽度为L的入射光以入射角θ照射在芯片上时,投射到凸点顶部区域的光经反射后在成像系统中形成光斑,投射到芯片基底上的光线经基底反射后在成像系统中形成长条形光斑。受透镜数值孔径的影响,凸点顶部仅有一小部分区域的反射光进入成像镜头,这一部分区域称之为“有效反射圆”。凸点顶部P在像平面上的成像为P′,光平面与凸点相切的切点为F,与基底相交于D点,入射光束边缘与芯片基底的交点为I、C,对应的像点分别为D′、I′、C′。沿X正方向移动芯片凸点时,由于半球体的拦光,使得基底上的光条上出现圆弧形缺口,移动过程中圆形缺口逐渐变大,圆弧顶点D′的位置也随着圆形缺口的变化而改变,此时反光点P′的位置也随之改变,如图中虚线所示。由于凸点顶部P与切点F所在光平面的距离固定,F点与D点相对位置不变,因此在凸点移动过程中P′D′的距离不会发生改变。根据不变量P′D′与凸点高度PO之间的几何关系可以精确计算出凸点的高度。
成像系统中P′D′的距离实际为QD的投影,找到PO与QD的关系就可以计算出凸点高度。PM为计算PO所作的辅助线,与凸点最高点P的入射光线重合,与EF相交于H点,其与QD和PO均存在几何关系,以PM为中间量可以推导出高度计算公式。图中PM=QD-QR-ND,QR和ND可以通过HF和入射角θ和凸点半径r计算出,HF=EF-EH,EF为凸点半径r。式(2)列出了部分参数的几何关系

图3(a)中QG=P′D′=x、PO=h,芯片凸点高度h与x和r之间的关系式为

式中,x为图3(b)所示的光斑中心至光条中圆弧顶部的距离,θ为入射光线相对芯片基板法线的夹角,r为凸点半径。式(3)中未考虑成像系统的放大倍率β,故将r=r′/β、x=x′/β代入式(3)后可得

式中,x′为加入放大倍率后凸点表面反射光图像中光斑中心与光条中圆弧顶部的距离,r′为加入放大倍率后光条图像中圆弧的半径,由于在实际试验过程中,投影装置和成像装置之间的角度θ很难标定,故考虑用其他参数进行间接标定的方法实现凸点高度的测量。将式(1)中的k=1/2βsinθ中的θ代入式(3)后得到

式中,光条中心位移与参考平面位移之间的系数k可通过一定标定流程得到,成像系统的放大倍率β也通过标定获得,r′和x′通过图像处理获得。以上参数的标定流程简单易行,从而避免了用式(3)进行凸点高度计算时θ值标定较困难的麻烦。
2 实验
2.1 实验装置搭建
实验装置如图4 所示,投影系统中LED 光源发出的白光经过狭缝和显微物镜后投射在待测物体表面,形成宽度为17~30 μm 的矩形光条。成像系统由无限远共轭显微物镜、无限远校正套管透镜和CCD 相机组成。相机为Basler 的piA2 400-17 gm,像元尺寸为3.45 μm、分辨率2 448×2 050。无限远共轭显微物镜能够实现平场成像,同时具有复消色差的功能,减小了镜头畸变对成像质量的影响。为了准确测量参考平面的位移,实验中搭建了基于激光干涉仪的载物台位移测量光路。

图4 芯片凸点高度测量实验装置Fig.4 Experimental device for measuring chip bump height
2.2 参数标定和计算
参数k的标定过程中使用垂直位移台沿Zw轴方向移动,以Agilent 激光干涉仪的测量结果作为位移台上参考平面在空间坐标系下Zw轴的坐标[22]。干涉仪的测量精度0.2 μm+0.1×10-6×L。标定时使用大恒光电的保护银平面镜作为参考平面[19],该平面镜的S1 面型为λ/4@633 nm。参数k采用最小二乘法拟合参考平面在Zw轴的坐标与图像上光条位移之间线性关系得到。
实验装置采用的显微物镜景深为14 μm,实验过程中光条偏离相机景深范围时容易出现图像模糊的情况。为了避免图像模糊影响标定精度,在标定之前采用基于Sobel 边缘算子的清晰度评价函数计算光条图像的清晰度,根据计算结果调整光条的位置,使得光条位于显微物镜的景深范围内[23]。
对采集的光条图像进行高斯滤波后使用灰度质心法提取光条灰度中心[25]。计算不同高度参考平面反射光条在图像坐标系下相对第一幅光条图像的位移Δx,表1 所示为干涉仪测量结果与图像中光条中心位移结果的对比,将Δx和ΔZw通过最小二乘法拟合后得到参数k。

表1 激光干涉仪测量位移与光条中心位移对比Table 1 Comparison between displacement measured by laser interferometer and strip center displacement
参数β是成像系统的放大倍率,标定时使用Halcon 圆点阵列标定板,标定板精度±1 μm,通过式(6)计算出像素当量K(μm/像素)[25]

式中,Pi是标定板上相邻圆点中心相距的像素数量,S是标定板上相邻圆点中心的距离(单位:mm),N是图像中参与计算的圆点的对数。已知相机像元大小为3.45 μm,成像系统放大率β=3.45/K。
本实验采用RANSAC 算法检测图像中的圆弧。该算法可使检测的圆弧更准确,随机噪声对检测结果的影响更小[26]。为了得到图像中圆弧的半径r,首先对图像进行高斯滤波,滤波后采用Canny 边缘检测算法提取圆弧区域的边缘,采用RANSAC 算法对获取的圆弧边缘进行圆拟合,并输出圆心坐标和圆的半径r′,图5 所示为沿光条方向截取的两个凸点图像,第一个凸点图像中,圆弧上绘制的圆即为RANSAC 算法的拟合结果。第1 节中凸点顶部反光点P′D′的距离x′的计算采用以下方法:首先在Canny 边缘检测的结果中挑选光条左侧远离圆弧区域的两个边缘点,计算两个点所在直线的斜率,根据反光点的几何中心与圆弧顶部点所形成的直线与光条垂直计算出x′。具体求解步骤如下:根据光条同一边缘的两个点计算光条的斜率,与光条垂直的直线斜率即可求解出,已知垂直于光条的直线的斜率和反光点几何中心坐标,在图像坐标系下求解该直线与圆方程的交点,反光点几何中心与该交点的距离即为x′。

图5 RANSAC 圆检测结果Fig.5 RANSAC circle test results
根据上述实验方案将图像处理的结果r′、x′代入式(4)即可计算出芯片凸点的高度,实验选取了16 个芯片凸点进行测量,芯片凸点的标称高度为50±5 μm。采用SENSOFAR 公司的3D 轮廓仪中白光干涉测量系统对上述16 个凸点进行高度测量,该测量系统的垂向分辨率为1 nm,测量10 μm 标准台阶的精度为0.5%,将此设备测量的结果作为凸点高度实际值,将本模型的测量结果与白光干涉仪的结果对比,得到图6所示的测量结果对比图,测量结果的均方根误差σδ=0.58 μm。

图6 芯片凸点高度测量结果Fig.6 Chip bump height measurement results
表2 为图6 中测量值与真值之差,从表中可以看出16 个凸点测量结果的误差均在±0.98 μm 范围内,仅有一个凸点的测量结果误差为1.071 μm,对测量图像观察发现,该凸点顶部存在灰尘颗粒导致阴影圆弧的边缘发生变化,影响了圆弧拟合的精度。由于是在实验室环境下开展的实验,无法避免灰尘对样品的污染,在实际生产现场检测设备均放置在百级洁净间中,因此可以避免灰尘对测量结果的影响。
2.3 精度评价
精确度反映了测量结果中系统误差和随机误差对精度的影响程度,可以使用测量的不确定度来定量评价[27]。本实验采用A、B 两类评定标准计算芯片凸点高度数学模型结果的不确定度。
根据式(4)可知不确定度的来源为:图像中反光点到圆弧顶部的距离x、检测的圆弧半径r、显微镜放大倍数β、系数k。采用A 类评定标准计算k的标准不确定度,对x、r、β的标准不确定度采用B 类评定标准计算。k通过最小二乘法拟合后得到,其95%置信区间的极限偏差为±0.001,故标准差σk=0.000 5,标准不确定度uk=1.67 ×10-4,自由度为9;由于Canny 算法的边缘提取精度是像素级别,因此图像的提取误差为3.45 μm。x服从均匀分布,其标准不确定度ux=3.45/ 3 =1.99 μm,自由度为∞;光条上圆弧半径r服从均匀分布,r的标准不确定度ur=1.99 μm,自由度为∞。β服从均匀分布,其变化量小于0.01,标准不确定度uβ=0.0058,自由度为∞。
由于r、x、β、k各个变量之间相互独立,测量结果的合成标准不确定度uc(h)计算公式为
式中,h对各个参数的偏导数通过式(4)得到,将r=90.30、x=292.09、β=3.83、k=0.1884 带入式(4)计算偏导数后得到uc(h)=0.378 μm。合成标准不确定度的结果h±uc(h)含被测凸点实际高度H的概率仅为68%。使用展伸不确定度U表征测量结果更加准确。

式中,包含因子n=tP(v),v是合成标准不确定度的自由度,计算公式为

将各个参数的标准不确定度和自由度代入上式后计算出v趋近于∞,根据t分布表查找显著度α=0.01时n=2.58,可得U=0.98 μm,即凸点高度的测量值h=49.78±0.98 μm,包含真值的概率为99%
3 结论
本文在光学三角原理的基础上提出了一种能够精确测量芯片凸点高度的数学模型,并通过实验验证了所提出的模型的准确性,测量结果的标准差和展伸不确定度均小于1 μm,相比于传统的光学三角法本文提出的高度模型的测量精度和速度有了进一步提升。若更换分辨率更高的显微物镜和相机,利用本文提出的数学模型测量结果的精确度将会进一步提高。本文研究结果对实现芯片凸点快速精确检测具有重要意义,对顶部是球形结构的微型物体的高度测量具有极强的参考价值。利用该测量方法结合高精度移动平台可以进一步实现对芯片或者全晶圆上凸点高度的测量,从而实现对凸点高度一致性的评价,本文方法对于工业在线凸点高度一致性测量系统的研究具有应用价值。
