纳弧度分辨的X 射线单色器布拉格转轴研究

刘孟廷，类维政，宋丽，夏思宇，凤良杰，董晓浩1，，王劼1，

（1 中国科学院上海应用物理研究所，上海 201800）

（2 中国科学院上海高等研究院，上海 201204）

（3 中国科学院大学，北京 100049）

（4 中国科学院西安光学精密机械研究所，西安 710119）

0 引言

基于加速器的先进X 射线光源具有高亮度、高相干性、高准直性等诸多优点，在物理、材料、化学、生命科学、微加工技术等领域展现出了优异性能，为科学研究和技术发展带来了重要的机遇［1-5］。把X 射线从光源点传输到实验装置的传输光路称为光束线，它是一个工作在超高真空中的高精度光机电设备，其X 射线的传输距离从几十米到几百米不等。利用不同功能的光学元件，如聚焦光学元件、分光光学元件等，光束线把光源点发出的X 射线选取出所需能量范围、能量分辨率、光斑尺寸、光束发散度等满足实验要求的光［6-8］。在光束线建设中，使用最多的就是大尺寸聚焦反射镜系统、光栅单色器、晶体单色器等，它们是保障光束线光学性能的核心设备。目前，同步辐射衍射极限环、X 射线自由电子激光装置等新一代光源在国内外不断涌现［9］，一方面对光学元件的性能需求有大幅提升，另一方面光学元件姿态的调整精度已普遍进入“微纳”范围，如光学元件的直线运动分辨率和转动角度的分辨率等要达到亚纳米和纳弧度量级。因此，研制超高真空或高真空兼容、具有纳米/纳弧度分辨、大负载的精密运动机械机构越来越成为国际上重要的发展方向，特别是在大转角范围内实现纳弧度角度分辨的运动机构，由于其要求高、应用场景多样，受到了广泛重视。

从机械原理上看，获得角度的方法通常有两种：1）利用高精度转轴直接转动，2）利用平移-角度转换机构，把平移运动转变为角度转动。在光束线单色器的应用领域中，前者的优点在于角度实现范围没有物理限制，但在大负载情况下，其角度分辨率基本在数百纳弧度量级，难以实现数十纳弧度的角度分辨率；后者可以获得很好的角度分辨率，但角度范围可能受限。

平移-角度转换机构的基本思想是所谓的正弦机构（sine-bar），如最简单的方法就是将一根刚性杆的一端固定在转轴上，推动另一端平动，从而得到角度。这种正弦机构的角度与平移是正弦关系，在实现角度-平移的高精度线性关系与使用的角度范围受到机械结构上的限制，所以多应用于X 射线光栅单色器［10］和反射镜的姿态调整［11］，晶体单色器和多层膜单色器等需要大角度工作范围的设备难以采用。解决这个矛盾的方法之一是在工程机械中广泛使用曲柄摇杆和正弦机构结合的曲柄滑块机构，如简单的对心式曲柄滑块和偏置式曲柄滑块机构等［12］。

类似机构在国际上已经有所发展。MARTEL K 等［13］为欧洲同步辐射装置（European Synchrotron Radiation Facility，ESRF）ID28 光束线设计了一种带有径向薄刀片的圆形车轮状柔顺机构，用于提升高分辨率背散射晶体单色器的性能，在线性驱动器驱动下可提供0.1 μrad 的角分辨率；SHU Deming［14］提出了一种新型高稳定多曲梁式旋转柔顺机构，并将其应用于晶体单色器和硬X 射线纳米聚焦Montel 镜系统，其角度分辨率优于50 nrad。近几年，Diamond 光源的ALCOCK S G 等［15］研发了一种超高精度角度发生装置，能够在7 000 μrad 范围内产生1 nrad 的步长。

本文设计了一种可用于X 射线晶体单色器布拉格角调整的偏置曲柄滑块机构，旨在利用纳米线性平动实现大转角范围内数十纳弧度的角度分辨。通常，角度的正弦与平移的线性关系对于晶体单色器的使用具有极大的便利性，通过建立连杆机构的模型，给出了偏置曲柄滑块机构的运动学关系，设计了大角度范围内的高精度角度正弦-平移的线性关系。该设计与机械柔顺机构相结合，在实验室得到了几十纳弧度的角度分辨率和十几纳弧度的角度稳定性。

1 物理设计

不考虑尺寸、变形、装配等误差时，偏置式曲柄滑块机构可简化为图1 所示的物理模型描述，r和l分别为曲柄和连杆的长度，L=r+l，e=LcosθBM为偏心距，Sc为滑块位置，分光晶体安装在曲柄处，入射到单色器晶体的X 射线沿Y的负方向入射，滑块沿X方向运动。该机构有3 个转动副，利用其中一处转动改变晶体法线方向与入射X 射线方向的夹角。图中θB为所需要的转动角度，即晶体的Bragg 角；当曲柄和连杆处于直线状态时，得到最大的Bragg 角θBM，对应的平移副位置标记为ScM，坐标轴的原点选取θB=0°时平移副的位置Scmin处，即Sc=0，因此平移副的净行程即为ScM。

图1 单色器晶体偏置式曲柄滑块机构示意图Fig.1 Schematic of the offset slider- crank mechanism for crystal monochromators

1.1 曲柄的转动范围和转动步长

晶体单色器的重要技术指标之一就是可输出的光子能量范围。根据X 射线晶体衍射的Bragg 方程式中，E为入射X 射线的光子能量，dhkl为衍射面的间距，则需要的光子能量范围由θB和晶体的衍射面（hkl）决定。在X 射线高能区，最经常使用的是单晶硅的高指数衍射面，如Si（422）衍射面。晶体的高指数衍射面由于Darwin 宽度较窄，需要极小的角度运动步长，本文按照Si（422）晶体单色器的基本要求，给出运动机构的设计。根据Si（422）的d422～1.108 Å（1 Å=0.1 nm）和ε=5.592 keV，在通常的10～50 keV 能量工作范围内，相应的Bragg 角为34°～6°（表1）。考虑到实际的一些因素，适当放宽运动范围是必要的，在本设计中我们取θB的设计范围为0～45°，优化的角度工作范围为5°～35°。

光子能量分辨率ΔE/E是晶体单色器需要达到的核心技术指标，可以由式（2）估算［16］。

式中，ωD为晶体衍射面的Darwin 宽度，Ψ0为入射X 射线光束的发散角。当不考虑热形变和其它应力导致的形变时，ωD可以在理论上给出计算值。为简单计，仅考虑平行入射X 射线光束情况，晶体Si（422）衍射面的主要物理参数和光子能量分辨率ΔE/E如表1 所示。

表1 硅晶体Si（422）衍射面的能量分辨率Table 1 Photon energy resolution of Si（422）

由于晶体的能量分辨率近似一个常量。换言之，在不同的能量点E处，能量分辨率对应的光子能量带宽ΔE是变化的，对于Si（422），由式（1）可得sinθB的分辨需求为

Δ(sinθB)≈1×10-6·sinθB（3）

对于晶体单色器的机械设计而言，其最小的角度运动步长δ（sinθB）应小于Δ（sinθB），根据晶体单色器的不同要求，一般地可以取δ（sinθB）在1/5～1/10Δ（sinθB）|min。由此，对于Si（422）晶体单色器，考察θB=5°时，由式（3）计算得Δ（sinθB）～87 nrad，取δ（sinθB）～15 nrad 是合适的。

综上所述，确定本文描述的偏置式曲柄滑块晶体调节机构的设计目标如表2 所示。

表2 偏置式曲柄滑块X 射线单色器晶体调节机构主要设计参数Table 2 Main design parameters of the offset slider-crank mechanism for crystal monochromators

1.2 偏置式曲柄滑块机构的几何尺寸

根据式（1），单色器选择的能量点与Bragg 角的正弦有关，若选择合适的几何关系，使得sinθB与Sc间形成高精度的线性关系sinθB≈A+BSc，将极大便于使用。

根据平移副和曲柄转动的几何关系，注意到在（0，ScM）范围内，始终存在直角三角形RtΔSPF 及其恒等式

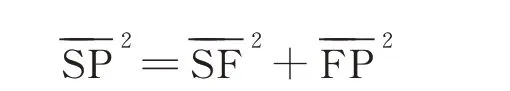
用前述定义的参数代入得

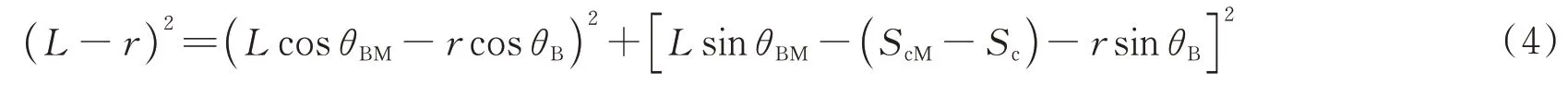
式中，L=r+l。利用式（4），将sinθB进行级数展开，并取前两项有

式（5）表明，在一定条件下，若可以忽略级数的高级次项，则偏置式曲柄滑块机构从线性距离转换为角度正弦的转换系数唯一地取决于曲柄长度，也就是说，对于同样的线性位移，曲柄长度越大，得到的角度正弦分辨率越小。但曲柄长度大，将使得机构的整体尺寸加大，转动惯量增加，需要根据应用需求平衡考虑。在晶体单色器的角度工作范围内，式（5）具有足够满足要求的精度是设计偏置式曲柄滑块机构的核心。

1）曲柄长度

对式（5）微分得到两种运动步长的传动关系

可根据sinθB的运动步长和平移步长的传动关系确定合适的曲柄长度。本设计中，δ（sinθB）～15 nrad，对于纳米滑动平台，若取运动步长为2 nm，由此得到

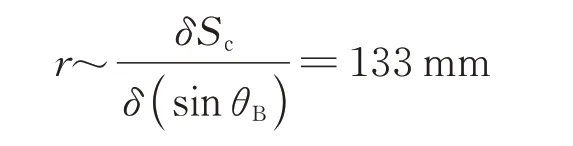
考虑到实际应用中存在的误差等因素，在设计中取r=140 mm。

2）连杆长度

性平移的传动比，和式（6）相比，计算出二者的偏差为

德城区位于北纬37°27′，东经116°18′56″，地处山东省西北部，德州市的中心城区，占地面积231 km2．北依京津，南靠济南，地处天津滨海新区和环渤海经济圈、济南城市群经济圈的重要节点．京沪高铁、太青高铁以及京沪铁路等5条铁路穿区而过，京福、衡滨等高速公路和多条国道、省道纵横交错，素有“九达天衢、神京门户”之称．

由于r是已知的，易推知式（7）是自由度θB和l的函数。图2（a）给出了在工作角度范围内式（7）表示的偏差曲线。可以看出，随着θB和l的变化，存在较为明显的变化。若在工作范围内，传动关系偏差值趋于0，可以认为式（6）具有足够高的精度。图2（b）中的实线为定义的平面与2（a）中曲面的交线，可以看出，随着θB的改变，只有当l是可变的，才能令式（7）在角度工作范围内均为0，这在实际设计中是难以实现的，也是没有必要的。一个合理的设计是选择一个固定的l值，使得在角度工作范围内，式（7）都有足够小的值，换言之，式（5）具有足以满足要求的精度。

图2 角度偏差模拟Fig.2 Simulation diagram of angle deviation.

考虑到偏离值取负值意味着分辨率优于要求值，因此，选择l时，以图2（b）中交线的左边部分为宜。即使如此，选择不同的l值，意味着优化的偏离不同。如当选择l为45 mm 左右时（交线的中点附近），则角度范围的两端均具有大的偏离值。我们希望在X 射线高能区，式（7）给出最好的线性关系，因此取l=55 mm，此时，Si（422）晶体单色器在其最常用的20～50 keV 内，优于3×10-5mm-1。

综上所述，根据Si（422）单色器的物理特性和应用需求出发，最终选取的曲柄滑块机械结构的参数见表3。

表3 偏置式曲柄滑块X 射线单色器晶体调节机构实际设计参数Table 3 Specifications of the offset slider-crank mechanism for the crystal monochromator.

2 结构设计

如图3 所示，此装置采用的是一种优化改良的曲柄滑块正弦机构，由直线位移平台、曲柄、连杆、连杆轴承和精密支撑轴组成。曲柄的一端装配在精密支撑轴的末端，该轴由精密加工的刚性外壳内的精密轴承实现光学元件稳定的角度旋转，而且为了在真空中运转，运动机构的转轴主要采用3 个陶瓷角接触球轴承支撑，采用背靠背的形式装配使转轴具有较高的刚度；曲柄与连杆由不锈钢制成，利用连杆轴承相连；连杆亦通过连杆轴承与线性位移平台上面的滑块相连。其中，选用的连杆轴承为C-Flex 圆柱形挠性轴承G-10，是一种零轴漂交叉簧片式柔性铰链，无摩擦无间隙转动，能够实现最大正负30°的角度旋转，具有较高的相对径向和轴向刚度。此外，根据大范围、高精度的应用需求，选择来自Micronix 的PPS-110 压电驱动直线位移平台。平台内集成了光栅尺，使其在闭环控制下具有2 nm的线性分辨率；利用MMC-103 控制器，行程范围可达到100 mm，以实现大的转角范围。

图3 偏置式曲柄滑块晶体布拉格角调节机构Fig.3 The offset slider-crank mechanism for the Bragg angle adjustment

与传统机构不同，该机构不仅精度高、可实现大范围的角度调节，而且位移与角度正弦的传动关系在几十度的范围内几乎保持线性；可以获得连续的纳弧度量级微角度输出；并且此装置在垂直于旋转面方向上同样具有较强的承载能力和刚度，能够扩展应用到垂直轴配置。

由于曲柄滑块机构优异的性能，将其结合高强度“Weak-Link”机构［17］应用到单色器中的双晶姿态调节。如图4 所示，正弦杆安装在平面转轴中心，是驱动机构的关键部件，用于第二晶体和第一晶体间的相对位置对准。两个平面形状的高刚度多曲梁式旋转柔顺机构模块分别安装在底板的两侧，外圈固定在底板上，内圈与第二晶体安装座和正弦杆的一端通过螺栓固定在一起，作为平面转轴的一对旋转轴承。同时，带有光栅尺的高精度压电陶瓷线性驱动器PPS-20 直接安装在底板上，在闭环控制下以2 nm 分辨率实现对第二晶体俯仰角的纳弧度量级微角度精密调谐。

图4 X 射线单色器晶体调节机构Fig.4 The mechanism for crystal’s adjustment of X-Ray monochromators

3 测量结果与讨论

3.1 角度测量方法

为了精确地检测此机构的性能，选用德国Attocube 公司的IDS 3010 激光干涉仪测量相对角位移，该干涉仪具有1 pm 的分辨率和10 MHz 的带宽，适用于超高压和低温条件，并且测量时不需要附加测量反射镜。测量原理如图5 所示，半导体激光器产生的红外激光束（波长为1 530 nm）在光纤端面被分成了两部分，一部分被直接反射用作参考信号，另一部分透射至由光纤端面和可移动测量目标形成的法布里伯罗腔，形成携带运动信息的测量信号。目标位移可以通过解调干涉信号的相位变化获得，关系为

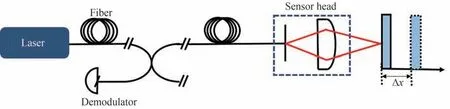
图5 F-P 激光干涉测量原理Fig.5 Principle of F-P laser interferometry

式中，λ为光波波长，ΔΦ(t)为相位变化量，ΔX(t)为测量目标的位移，p为F-P 腔的折叠次数。由于不同的传感头配置提供不同的F-P 腔结构，根据超高精度的测量需求，选取了聚焦型传感头（F=40 mm）。经更高精度测量设备的标定，结合聚焦传感头，干涉仪的测量精度优于0.1 ×10-6，测量距离约38.5～41.5 mm。

角度测量方法如图6（a）所示，使用两个传感头，分别测量测量目标不同端部的线性位移，则角位移为

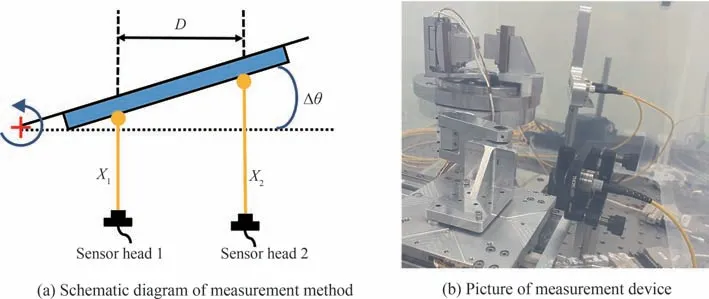
图6 角度测量方法Fig.6 The method of Angle measurement

式中，Δθ为角位移，X2-X1为目标两端的相对线性位移，D为两端测量位置间的距离。该方法计算简单，然而，测量误差会降低这种间接测量方法的准确性，这对于纳弧度尺度的测量尤为关键。为此，由式（9）估算测量误差有

对于第一项相对位移测量误差，引起的原因主要为两个传感头分别和初始测量平面的非正交性引起的余弦误差，使实际位移Xa与测量位移Xm间的关系为

β为测量轴与目标轴间的角度偏差。由于所选传感头容许的最大偏差为0.35°，D为40 mm，经式（9）～（11）计算得，在小于50 nrad 的角度测量步长下，此项测量误差极小，可忽略。对于第二项测量间距误差，引起的主要原因为传感头支撑架加工误差和两个传感头姿态调节误差。经式（9）、（10）推导得角度测量误差与测量间距误差关系为

由于传感头容许的偏离角度和设备加工精度的限制，δD小于1 mm。因此，由式（12）可推算得，在小于50 nrad 的角度测量步长下，此项测量误差也极小，可忽略。

分析证明，在使用聚焦型传感头，测量范围极小的情况下，测量误差引入的不确定度极小，均可忽略。因此，利用皮米分辨F-P 激光干涉仪可实现小于50 nrad 的角度分辨测量。

3.2 测量结果与分析

为了克服温度波动、湿度和振动等因素对测量结果的干扰，测量环境选为地下一层温度波动≤±0.1 ℃的千级光学洁净间，并将该机构置于光学隔振平台上，罩上简易罩防止气流扰动，如图6（b）所示。共有三个传感头参与测量，其中两个传感头用于测量传动角，另一个传感头用于测量位移台的线性位移。

1）传动关系

在行程范围50 mm 情况下，计算得传动角度范围约为21°。由于传感头限制角度测量范围至0.35°，为了更全面地验证曲柄滑块正弦机构的传动性能，分别在直线位移台所利用工作行程的不同位置处进行了传动关系测量，测量结果如图7 所示。蓝色实线为理论值，红色点为实际测量值，该值由直线位移台以6 nm 步长连续运动十个步长时，对每个步长稳定后的位置进行线性拟合得到的。结果显示，在每个位置测得的传动关系均接近理论值，误差均小于10%。

图7 传动关系测量结果Fig.7 Measurement results of the transmission ratio

2）最小步长

对于晶体分光元件的应用，最重要的参数之一是机构能够可靠地提供最小步长。位移台分辨率为2 nm，但在实际测量时发现2 nm 步长下位移台无法行走，推测可能是2 nm 情况下位移台的推力不足，故测量时选择了4 nm 步长。由图8（a）可见到4 nm 运动步长下监测到了明显的角度台阶。取各台阶面的平均值作为台阶高度，并将各台阶高度差取均值，此即Bragg 角度的最小分辨步长，计算得到此分辨为31.20 nrad，标准差为3.07。

在实际测量中发现，当步长大于6 nm 时，出现了明显的过冲现象，如图8（b）所示。我们认为这是由于当滑动步越大，最终达到的速度越大，当滑块突然停止后，由于惯性作用，使得滑动产生较大的过冲，从而在角度台阶上出现了此现象。角度过冲的平均值约为46 nrad，由此可以估算出滑块的过冲值δSc～r·δθB=0.139 5×46=6.41 nm，这与我们用激光干涉仪直接测量同样质量负载下滑块的过冲比拟。

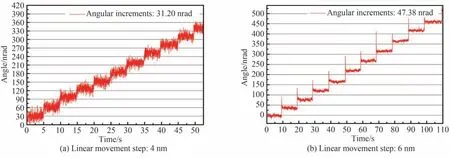
图8 角度运动步长测量结果（Sc=0 mm 处）Fig.8 Measurement results of angular increments（Sc=0 mm）

3）角度稳定性

为了保持光束线的性能，运动机构在给定角度时还需要保持一定的稳定性。图9 给出了Sc在0 mm 附近的稳定性测量结果。稳定性测量时长为800 s，振动采样率为50 Hz。计算得角度漂移量的均方根值为15.18 nrad。

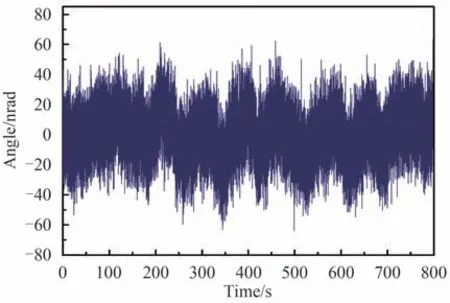
图9 角度稳定性测量结果Fig.9 Measurement result of angular stability

4 结论

为了满足新一代大科学装置的需要，研制了一套纳弧度分辨的偏置式曲柄滑块X 射线单色器布拉格角调节机构。分析了曲柄滑块机构的运动学关系，基于X 射线晶体单色器应用能量范围、能量分辨率和特殊的线性传动关系的需求，提出了设计指标，建立了连杆机构参数的优化模型，实现了大角度范围内的高精度角度正弦-平移的线性关系。最后，利用皮米分辨F-P 激光干涉仪结合高精度角度测量方法，对此装置的传动性能、分辨率和稳定性进行了测量。结果显示，此装置传动关系误差小于10%，并且可利用纳米线性位移台在实验室实现31.20 nrad 的最小步长和15.18 nrad 的稳定性。此装置中的柔顺机构和高精度角度测量方法将对未来集成精准调控反馈系统，实现先进光源中光学元件高稳定的实时精密调控，以获得高质量的X射线光束具有重要应用意义。