残差时间计数型InGaAs 脉冲频率调制数字读出电路研究

王绪泉，汪鸿祎，张永刚，黄松垒，方家熊

（1 中国科学院上海技术物理研究所传感技术联合国家重点实验室，上海 200083）

（2 中国科学院上海技术物理研究所中国科学院红外成像材料与器件重点实验室，上海 200083）

（3 中国科学院大学，北京 100049）

0 引言

近红外（Near-infrared，NIR）光谱分析技术具有快速、无损、高效率的特点，是物质成分分析的重要手段［1-2］。近年来，便携式微型光谱仪和光谱传感物联网的发展推动了光谱分析技术向野外现场分析和在线检测应用拓展［2-6］，这对红外光谱传感器的动态范围和抗干扰能力等性能提出了更高的要求。与传统模拟读出方式相比，数字读出电路通过在红外焦平面的列级或像素级位置集成模数转换器（Analog to Digital Converter，ADC），缩短了模拟信号通路，有益于增加信号传输的抗干扰能力［7］。数字读出电路是红外焦平面片上数字信号处理的前提，是红外智能传感器发展的关键技术环节，根据应用需求选择集成不同的数字化结构，可有效提升信号读出质量和焦平面性能。

脉冲频率调制（Pulse Frequency Modulation，PFM）型数字读出电路结构，又被称作电荷包计数型结构，可以在一个积分周期内对积分电容多次复位，将探测器的光电流转化为数字脉冲［7-10］。由于光电流大小与产生的数字脉冲频率成正比，因而可以使用积分时间内的脉冲累加计数值作为数字码值，实现探测器光电流的数字积分。传统结构的数字读出电路，如单斜率型、逐次逼近性和过采样型等，都是在对红外探测器的光敏电流进行模拟电压积分，因此难以突破电压摆幅和电容大小决定的“天花板”限制。PFM 结构通过多次复位打破了常规读出电路中积分电容和电源电压决定的满阱电荷容量限制，是一种实现超大动态范围焦平面信号数字读出的可行技术方案。PFM 结构较为简单，除输入级和比较器工作在模拟域，其余部分均工作在数字域，因此常被作为焦平面像素级数字化方案的选择之一［7］。PFM 结构的最小有效位（Least Significant Digit，LSB）取决于积分电容一次复位的最小电荷量。由于工艺限制，积分电容不可能做到无限小，因此最后一次复位后积分电容上的残余电荷会引起转换误差［8］。为了进一步提升转换精度和动态范围，基于粗略转换和精细转换相结合的多种两步式PFM 转换结构被研究者提出和应用［8-10］，通过两种转换方式相结合，强光下以粗略转换为主扩展动态范围，弱光下以精细转换为主提取信号细节，可以进一步满足多场景的光谱应用需求。此外，在对强光照环境下的探测器光电流进行积分时，PFM 数字化结构还存在转换结果线性度较差等问题［8］。

短波红外InGaAs 探测器多采用电容负反馈放大（Capacitance feedback Trans-Impedance Amplifier，CTIA）输入级结构［11］，目前关于CTIA 输入级的PFM 数字读出电路研究还相对较少。本文分析建立基于CTIA 输入级的PFM 数字化结构转换模型，针对残余电荷带来的转换误差和复位遗失电荷引起的转换非线性问题，进一步设计了一种线列光谱组件的双积分电容残差时间计数型两步式PFM 数字读出电路，实现了16 位粗略转换和最大16 位精细转换融合，为短波红外光谱组件的野外复杂场景应用提供了一种大动态范围的数字读出方案。

1 理论转换模型

CTIA 输入级PFM 数字读出电路的结构如图1（a），单元电路主要包括CTIA 输入级、比较器、复位电路、计数器和存储器等。探测器的光生电流信号在CTIA 输入级积分，当积分电容负端电压低于比较器参考电压时，比较器输出翻转对积分电容快速放电复位，此过程周期形成一个脉冲信号作为ADC 的LSB。在信号积分周期内，积分电容多次复位，通过计数器对脉冲个数的计数码值表征探测器光电流的大小。

CTIA 输入级PFM 数字化结构的转换过程主要存在两个比较重要的非理想因素，一是最后一次脉冲复位后积分电容上存在的残余电荷，由于该部分电荷未被纳入量化，因而会引起转换误差；二是实际复位过程中，复位脉冲和复位电流会导致部分积分电荷遗失，分别对其展开讨论。

首先分析积分电容残余电荷带来的影响，将电容的积分复位过程看作理想状态，一个积分周期的总积分电荷可以表示为

式中，Qint表示积分电荷；N表示脉冲计数码值，是光电流大小转换后的数字表征；Q0表示积分电容在两次复位之间的积分电荷量，其值由积分电容大小C和复位前后的电压差ΔV决定；Qres表示积分电容上的残余电荷，大小介于0 和Q0之间，可知残余电荷引起的误差最大为1 个LSB。由式（1）可得，积分电容残余电荷带来的转换误差ϵ可以表示为

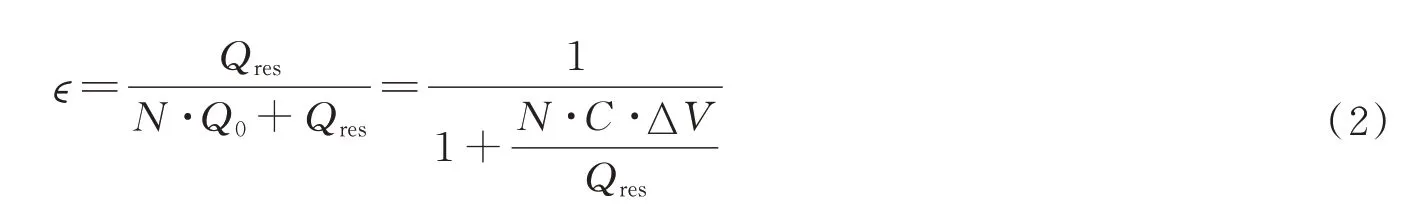
由式（2）可知，随着N增大，ϵ值不断减小最终趋向于0，说明残余电荷引起的误差仅在小积分电流情况下比较明显，随着积分电流增大，残余电荷的影响逐渐减弱。

对遗失电荷的分析需要着重关注电容积分复位过程的细节，因而将总积分电荷表示为

式中，Q′0表示电容在两次复位之间的有效积分电荷量；Qr表示单次复位过程中的遗失电荷，Qrst为总的遗失电荷。由以上分析可知，在大积分电流情况下，残余电荷Qres引起的转换误差可以忽略。采用注入电流与积分时间的乘积表示电荷量，则式（3）可表示为

式中，Ttotal代表总的积分时间，I为实际积分电流，Trst为复位脉冲的宽度，由比较器反转速度和整形电路的延迟时间共同决定。对式（4）进行变换，可得转换后的数字化码值N为

Ttotal、Trst、C在特定的电路参数和应用环境下为常量，着重分析I和ΔV的非理想变化趋势。因为PFM结构留给积分电容的复位时间极短，复位结束时电容上的复位电流Irst不会立即消失，由电路知Irst与探测器电流Id反向，故积分电流并非在所有时刻都与探测器电流相等，其与时间的函数关系可表示为

式中，τ为CTIA 电路复位时的响应时间常数，与CTIA 运放、探测器电容、复位开关和负载等有关。进而可推出ΔV的函数关系式为

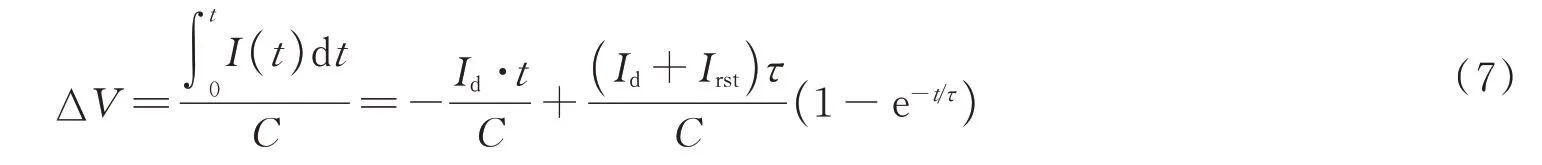
由式（7）可知，在非理想条件下，由于复位电流的影响，运放输出端信号如图2，在复位过程（阶段1）结束后先非线性上升（阶段2）再线性下降（阶段3）。此外，ΔV还会受到偏置电压Vref和Vcm引入的噪声影响，因此在实际应用中需要尽量为这个两个偏置电压选择高精度、高稳定性的解决方案。由于ΔV和I均受到复位电流的影响，为了简化数学模型，使用指数因子p表征复位电流引入的非理想因素，将N表示为

图2 CTIA 输入级PFM 数字读出电路的非理想复位Fig.2 The non-ideal reset of pulse frequency modulation digital readout circuit with CTIA input stage

式中，N与积分电流I成典型对数关系，而理想转换值与I成线性关系，故在强光照条件下，随积分电流I增大，转换值N线性度逐渐恶化。在同样的应用场景下，一个较小的积分电容有较高的转换精度，与之同时会导致更多的“积分-复位”循环，因而常规PFM 结构需要在转换精度和转换线性度之间进行设计折衷。

2 电路设计与验证

短波红外InGaAs 探测器在常温下的响应波长可达1.7 μm，通过调节铟的组分可以将截止波长扩展到2.5 μm。由于所探测的波段含有丰富的光谱特征信息，InGaAs 探测器被广泛应用于近红外光谱分析设备之中。以目前短波红外光谱传感物联网中微型光谱仪常采用的256×1 线列光谱组件为例［3-5］，为了提高能量利用效率，256 个50 μm×500 μm 长条形光敏元呈“一字型”排列，响应波段0.9～1.7 μm，峰值探测率≥1.0×1012cm·Hz1/2/W。根据探测器的R0A因子估算得出探测器零偏微分电阻约4 GΩ，探测器电容约10 pF，光电流输出约在nA 到μA 量级。基于上述探测器条件，针对256×1 线列光谱组件开展了双积分电容残差时间计数型两步式PFM 数字读出电路的设计和仿真验证。

2.1 单元电路结构设计

基于第1 节分析，可知当脉冲计数值较小时，CTIA 输入级PFM 结构的转换误差主要由残余电荷引起；随着注入电流增大，遗失电荷成为导致转换非线性的主要原因。针对CTIA 输入级设计了两步式PFM 数字读出电路单元，对残余电荷和遗失电荷引起的转换误差进行改善，其结构如图1（b）。

针对残余电荷引起的误差，采用脉冲计数粗量化加时间计数精细量化校正的两步式转换方法予以改善。如图3，在常规积分时间结束后，继续积分过程直至产生一次额外脉冲，采用高速时钟对INT 信号下降沿和脉冲上升沿之间的时间计数，残差时间计数值作为精细量化结果与脉冲计数值进行融合得到最终数字码值［9］

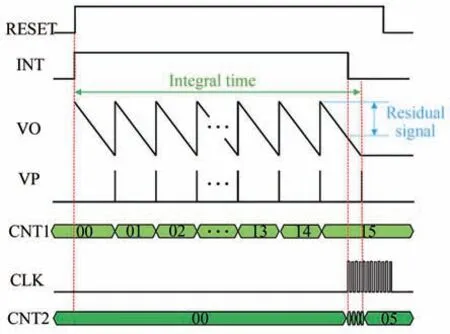
图3 残差时间计数型两步式PFM 数字读出电路时序图Fig.3 The timing diagram of two-step residual-time-counting pulse frequency modulation digital readout circuit

式中，Tc为从粗略转换时间，即INT 高电平时间，N为粗略转换码值，n为精细转换码值，f为时钟频率，Tc+n f为总积分时间。

为了改善遗失电荷导致的转换非线性，最直接的措施就是减少复位次数。如图1（b）所示，电路采用50 fF（Cmin）和1 pF（Cmin+Cmax）两档积分电容。在弱光模式下使用小积分电容提升转换精度，在强光模式下使用大积分电容控制“积分-复位”次数，保证焦平面在强弱光环境下均有较好的线性度。与此同时，残差时间计数型两步式结构可以保证在采用大积分电容情况下仍有较高的分辨率性能。

2.2 电路实现与仿真验证

256×1 线列光谱组件的封装方案为两条128×1 电路在光敏芯片上下布局，通过引线互联叉指读出。电路采用0.18 μm CMOS 1P6M 模数混合工艺设计，其中模拟部分采用3.3 V 电源电压，数字部分采用1.8 V 电源电压。CTIA 部分采用常规的套筒式共源共栅结构运放，比较器是模拟部分的关键模块，采用了经典的自偏置互补差分比较器结构，如图4 所示。采用多级反相器级联进行脉冲整形。单元电路的数字部分和整体ALU 部分采用RTL 级硬件描述性语言设计，经过综合、自动布局布线后完成与模拟部分的版图集成。电路包括脉冲计数粗略转换精度16 bit 和残差时间计数精细转换精度最大16 bit，在VREF为2.5 V，Vcm为1.25 V情况下，采用50 fF 和1 pF 工作的理论满阱容量可达25.6 Ge-和512 Ge-。

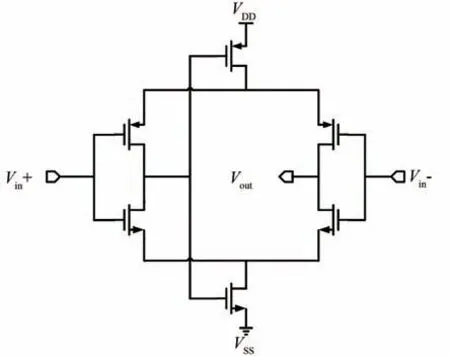
图4 自偏置差分比较器电路图Fig.4 The circuit diagram of complementary self-biased differential comparator

针对短波红外光谱组件应用，在探测器零偏微分电阻4 GΩ，探测器电容10 pF 的条件下，使用传输门作为复位开关，对图1（b）所示两步式PFM 数字读出结构进行仿真。其中，比较器输出脉冲经多级反相器整形后控制传输门开启，对积分电容两极短路完成放电，仿真结果显示脉冲宽度约1 ns。在INT 高电平时间设置为3 ms，时钟频率1 MHz 的情况下，结果如图5、图5（a）为理想情况下理论计算值与实际电路仿真转换码值对比。相比理想状态下的线性转换结果，实际转换值因为复位遗失电荷的影响呈现出非常典型的对数特性，与理论分析相符。图5（b）重点关注小积分电流情况下粗略转换和两步式精细转换融合后的结果对比，可以看到精细时间计数对于积分电容残余电荷引起的转换误差有较为明显的改善作用。针对常规PFM 结构的转换精度和转换线性度矛盾，采用两档积分电容予以改善，效果如图5（c），在大积分电流时分别使用小积分电容和大积分电容，转换值非线性度分别是0.62%和0.06%，线性度得到了显著提升。根据室温条件下1.7 μm 常规InGaAs 探测器的典型暗电流密度，计算得到50 μm×500 μm 光谱组件的典型暗电流约为百pA 量级，采用所提出的两步式脉冲频率调制数字读出电路，仿真结果表明，从ADC 量化角度，可实现远大于100 dB 的大动态范围光电流转换。同时，该数字读出电路可以兼容小光敏元探测器应用，通过提高精细时间计数的时钟频率，可以进一步提高精细转换的分辨率性能。

图5 残差时间计数型两步式PFM 数字读出电路仿真结果Fig.5 The simulation results of two-step residual-time-counting pulse frequency modulation digital readout circuit

所设计的残差时间计数型PFM 数字读出单元的电路版图如图6，尺寸约为90 μm×200 μm。形成的两个128×1 阵列单元中心距100 μm，尺寸约为15 mm×2.7 mm，256×1 光谱组件峰值功耗小于20 mW。通过对各模块分别进行功耗分析，发现主要功耗来自于比较器工作时的高速翻转。当光强固定时，比较器翻转的频率也是相对固定的，考虑到实际应用中的积分时间极短，一般将光注入电流看做定值。因此，可以在下一步的设计改进中尝试改变电路结构，通过对少数几次比较器翻转产生的脉冲进行频率测量，来避免比较器长时间多次翻转引起的功率消耗，进一步满足短波红外焦平面光谱组件野外应用的低功耗需求。

图6 残差时间计数型两步式PFM 数字读出电路单元版图Fig.6 The unit layout of two-step residual-time-counting pulse frequency modulation digital readout circuit

3 结论

建立CTIA 输入级的PFM 结构理论模型，分析积分电容残余电荷和复位遗失电荷引起的转换误差和线性度问题。提出了双积分电容残差时间计数型两步式转换方案，基于0.18 μm CMOS 工艺设计了针对256×1 线列InGaAs 光谱组件的CTIA 输入级PFM 数字读出电路，对残余电荷和复位遗失电荷引起的转换误差和线性度问题予以改善，仿真结果表明，该电路实现了16 位脉冲计数粗略转换和最大16 位残差时间计数精细转换相融合，为红外焦平面的野外复杂场景光谱应用提供了一种大动态范围数字读出方案。由于该电路结构在面阵焦平面的应用中会受到版图尺寸和功耗限制，后续设计中可以改用更小线宽的工艺制程，并进一步在电路结构和参数方面进行优化调整。