拓扑光子晶体与超构光子学（特邀）

张硕实，何辛涛，陈晓东，董建文

（中山大学物理学院光电材料与技术国家重点实验室，广州 510275）

0 引言

随着信息技术的发展，微纳光场的调控和处理技术逐渐受到人们的重视。集成光学是开展微纳光场调控研究的重要体系，研究人员在集成光学中展示了许多有趣现象，并提出了各种实际应用诸如全光开关、光逻辑门和集成光电路。但与此同时，一些基本问题也制约着光信息技术的进一步发展，其中一个重要问题就是由制造误差引起的不可忽略的光散射损耗。为了克服这一问题，人们除了改进制造工艺外，还尝试从物理原理上取得突破。而拓扑光子学是解决上述散射损耗问题的一种新方法。拓扑学起源于数学，它是研究几何图形或空间在连续改变形状后保持不变的性质的学科。例如，闭曲面是以“洞”的个数来分类的，定义为亏格。亏格在形变过程中保持不变，不会撕裂或合并。因此将拓扑学引入光子学可以描述对某些扰动具有抗散射特性的现象，有望实现对缺陷、无序免疫的光传输现象。

拓扑光子学启发自最初在固体物理学中理解物质拓扑相的思想，这个领域的研究始于1980 年KLITZING K V 等在实验上观察到的量子霍尔效应［1］。他们先对二维电子气施加周期性磁场再施加电场，观察到了类似传统霍尔效应的电流，实验发现霍尔电导率是磁场的函数且恰好是e2/h的整数倍，这就是整数量子霍尔效应。随后THOULESS D J 等给出了相应的理论解释［2］，霍尔电导率中的整数部分与系统的一个拓扑不变量有关，这个拓扑不变量就是陈数（陈省身数）。它是一个整数且与动量空间中布里渊区内的所有电子波函数有关，反映了整体的拓扑性质。为了将这一拓扑不变量和物理相联系，拓扑绝缘体的体边关系理论被提出［3］，即将两块具有不同拓扑不变量的材料拼接在一起，相接面一定会出现空间局域的模式，且能量处于周围材料的体态禁带内。关于体边关系有一个定性的理解，即两条不相交能带的拓扑不变量在微扰下不可能改变，除非微扰引入了能带的交叉。那么两块具有不同拓扑不变量的材料拼接在一起后，它们能带的拓扑不变量是不同的，所以能带必须要相交来改变拓扑不变量，且相交点一定处于上下能带之间，这就带来了体态禁带中的模式，这种模式表现为空间局域［4］。在量子霍尔效应中，边界态具有单向传输的特性，即电子不能向反方向移动，这种性质在凝聚态物理领域称作手性（这里与光学中的手性定义无关）。这种性质导致边界态对背向散射免疫，即结构缺陷无法耦合出反向传输的模式，带来电子传输的高抗散射性。这种现象的物理本质是时间反演对称破缺的必然结果。可以证明，陈数非零一定要引入时间反演对称破缺，因此对结构设计的要求较高。为了在时间反演不变系统中引入拓扑理论，量子自旋霍尔系统或Z2拓扑绝缘体被提出［5，6］。在这类系统中，陈数保持为零，为此人们定义了新的拓扑不变量（即Z2数），在时间反演对称下可以非零，相应地会出现自旋关联单向传输的边界态。拓扑理论的引入为边界态的设计开辟了全新的道路。2008 年，HALDANE F D M（2016 年诺贝尔物理学奖得主之一）和RAGHU S 首次将拓扑理论引入光学系统［7］。随后，类比固体物理中的拓扑理论，基于类量子霍尔、类量子自旋霍尔、类量子能谷霍尔效应的拓扑光子晶体理论被陆续提出并实验验证，开辟了拓扑光子学这条全新的道路。

超构光子学基于人工结构的设计实现多维度光场调控，因其结构的多样性丰富了光物理与光应用。依托超构光子学原理开发的微光学器件与系统，近年来逐渐在包括光子集成电路、显微成像、近眼显示、光量子计算、量子精密测量等国家关键科技领域展现出巨大的应用潜力，成为备受瞩目的变革性技术。人们借助拓扑光子学理论研究光子晶体、超构表面等超结构，提出并实现了大量新奇的光学现象且设计制作了各种高性能指标的光学器件，为超构光子学开启了拓扑光子学这一重要分支。超构表面是由许多亚波长微纳结构以特定的人工排列组合成的一种微纳平面光学元件，能够在亚波长尺度下实现对光场振幅、相位、偏振、频率等特性的精准操控，从而获得所需的光学元件性能。光子晶体是材料折射率在空间维度上呈周期性分布的人工亚波长光学结构，具有良好的光场约束、多自由度调节和集成能力。二者都是研究拓扑光子学的良好载体。本文将着重介绍拓扑光子晶体的发展历程与研究现状。

光子晶体（Photonic Crystal，PC）作为具有代表性的微纳光场调控体系，在多种拓扑相的实现和拓扑光子学器件应用中起着重要的作用。由于光在周期性光子结构中的布拉格散射，光子晶体具有光子带隙。如果光的频率位于光子晶体的禁带内，光就不能在光子晶体中传播，这与电子禁带的性质相似。由于拓扑物理最初用来研究周期势场中的电子传输行为，因此同样具有周期性结构的光子晶体被认为是研究拓扑光子学的理想系统之一。而近年来，研究者们通过在光子学中实现拓扑结构，的确可以揭示新的物理原理和解决实际问题。在拓扑光子晶体（Topological Photonic Crystal，TPC）中，许多物理原理和器件应用已经在理论上提出并在实验上实现，如单向传输［8］和抗散射传输［9］。由于光量子在量子计算和量子信息中的巨大潜力，近年来人们开始追求在实验上实现各种光量子行为。已有不少工作尝试用拓扑光学结构来实现拓扑保护的单光子源［10］、双光子态［11］和Hong-Ou-Mandel（HOM）干涉［12］。而后来研究人员发现，在拓扑光子晶体中也可以实现各种光量子行为，如HOM 干涉［13］。种种研究表明，拓扑光子晶体在微纳集成光子与光量子器件中拥有极大的潜力。本文将介绍拓扑光子晶体的发展历程和研究现状，概述类量子霍尔光子晶体、类量子自旋霍尔光子晶体和类量子能谷霍尔光子晶体的物理特性和设计方法，同时介绍拓扑光子晶体在光传输、无源器件、有源器件、光量子器件中的潜在应用。

1 拓扑光子晶体的物理特性和设计方法

1.1 基于类量子霍尔效应的拓扑光子晶体

量子霍尔效应是固体物理中的拓扑现象之一。在量子霍尔效应中，电子沿系统边界传输，从而产生手性边界态。手性边界态来源于体带的非平庸拓扑性质。它们具有独特的单向性，且对无序有很强的抗散射性。类比量子霍尔效应，可以在光子晶体中实现类似的现象，这种光子晶体被称为类量子霍尔光子晶体（Quantum Hall PC，QHPC），以下简称类霍尔光子晶体。作为霍尔光子晶体的开创性工作，HALDANE F D M 和RAGHU S 将拓扑物理引入光学系统［7，14］，研究了基于二维旋电材料的三角晶格光子晶体结构，在理论上预言了对特定结构外加磁场可以类比量子霍尔效应实现光的单向传输。在二维光子晶体中，一个体带的陈数定义为

式中，Ω(k)是贝里曲率，Ann′(k)≡iunk|∇k|un′k是贝里连络，unk是第n个体带布洛赫函数的周期部分。陈数表征了光子能带的拓扑性质。时间反演和空间反演对称性的结合允许在横向电场（TE）模式的第二和第三体带之间出现狄拉克点［图1（a）］。狄拉克点周围的等效哈密顿量具有二维无质量狄拉克方程的形式为

式中，δk是到布里渊区原点的距离，σ̂i是作用在对应于二重狄拉克简并的子空间上的泡利矩阵。在狄拉克点附近，等效哈密顿量对应于线性色散ω(δk)-ωD=±νD|δk|。当外加电场时，旋电介质的介电常数张量将具有非零的非对角元素，导致时间反转对称性被破坏，出现光子带隙。等效哈密顿量将添加一个质量项，并变为

式中，κ与旋电介质与背景材料的介电常数张量中非对角元素的虚部之差成正比。在狄拉克点附近的色散变为，它表现了一个宽度为2|κ|的频率带隙。在这个带隙之下，第二个带获得一个非零的陈数。根据体边对应关系，当这种拓扑上非平庸的光子晶体（陈数为非零）与平庸的绝缘体（陈数为零）形成边界时，禁带中将存在单向边态。

实验上，霍尔光子晶体最早由WANG Zheng 等在微波段实现［8，15］。结果表明，不受狄拉克点的限制，单向模式可以推广到二维旋磁光子晶体。他们在旋磁材料中设计了正方晶格光子晶体［15］。这种结构没有狄拉克点，但在M点发现了横向磁场（TM）模式的第二和第三能带之间的简并［图1（a）左图］。通过外加磁场打破时间反演对称性，导致能带分裂，得到了非零陈数的完整带隙［图1（a）右图］。在旋磁光子晶体（拓扑非平庸）与完美电导体（拓扑平庸）的边界处出现了无反射的单向边界态。实验样品为二维旋磁光子晶体，由铁氧体YIG 圆柱在空气排列成正方晶格组成［图1（b）］。在旋磁光子晶体与金属包层的界面上发现了手性边界态。即使在通道中放置长金属散射体［图1（b）］时，边界态也展现出了抗散射传输的能力。

图1 磁光光子晶体的能带与边界模式Fig.1 Band structure and edge states of magneto optic PCs

自从理论提出和首次实验验证以来，霍尔光子晶体在不同的结构中得到了广泛的研究，以实现新颖的光传输行为［16-21］。例如，AO Xianyu 等考虑了蜂巢晶格旋磁光子晶体结构，并在锯齿形带状边界显示了单向边界态［16］。在这种蜂巢状晶格中，即使边界暴露在空气中，边界态的单向传输对锯齿形边界上的缺陷也不敏感，称之为自引导拓扑边界态。随后，POO Yin 等对这种自引导电磁边界态进行了实验验证［17］。他们将周期性铁氧体棒排列成蜂巢晶格，在非平庸带隙中发现了拓扑手征边态。此外，多模单向波导被提出并在具有大禁带陈数（即陈数绝对值大于1）的旋磁光子晶体中实现［18，19］。根据体边关系，边界态的数量由陈数差决定，所以实现大禁带陈数，可以在空气边界处出现多条色散曲线，即多模单向波导。在蜂巢晶格的基础上，如果对一个原胞内的两个旋磁晶体柱分别施加不同方向的磁场，便可以实现反手性的边界态［20］，即上下边界的边界态手性方向相反。2021 年，WANG Mudi 等实验实现了支持单向边界模式的旋磁光子晶体［21］。

1.2 基于类量子自旋霍尔效应的拓扑光子晶体

在实现类量子霍尔效应的光学系统中，需要强磁光响应并外加磁场来打破时间反演对称性，获得拓扑非平庸带隙。这些条件限制了类量子霍尔光子晶体的进一步应用，特别是旋磁材料的磁光效应在光学波段上很弱，且吸收不可忽略。因此，需要时间反演不变的拓扑光子晶体。

类比量子自旋霍尔效应实现的拓扑光子晶体是类量子自旋霍尔光子晶体（Quantum spin Hall PC，QSHPC），以下简称自旋光子晶体，它是一种时间反演不变的光子晶体。根据Kramers 定理，电子系统的拓扑保护Z2相必然导致简并对的出现。电子系统中的Kramers 简并可以由电子的自旋向上和自旋向下态组成，然而在光子系统中并非如此。在光子系统中实现类量子自旋霍尔效应并不简单，因为光子不具有半整数自旋且不受费米统计的影响。因此，在光子系统中实现类量子自旋霍尔效应首先需要构造一对赝自旋。迄今为止，构造光子赝自旋的方法多种多样，如利用电磁对偶超结构［22-25］或光子晶体的晶体对称性［26-32］。

KHANIKAEV A B 等提出了在光子晶体中实现类量子自旋霍尔效应的早期工作［22］。一般而言，当光波在二维介质中传播时，由于介电常数和磁导率张量（即ϵ̂和μ̂）不同，含Ez分量的TM 波和含分量的TE 波具有不同的传播常数。若考虑ϵ̂=μ̂的电磁对偶超结构，光子赝自旋态可以由TM 波和TE 波的线性组合构成。这两个赝自旋态是双重简并的，互为时间反演对称关系。此时，三角晶格光子晶体中会出现具有四重简并的狄拉克点［图2（a）］，其等效哈密顿量的形式为

式中，σ̂i、ŝi和τ̂i是作用于二重狄拉克简并、赝自旋和能谷子空间上的泡利矩阵。最后一项ζτ̂z ŝzσ̂z打开了一个宽度2|ζ|的带隙。决定类量子自旋霍尔性质的量化拓扑不变量，自旋陈数，定义为Cs=(C+-C-)/2，其中C+（C-）是赝自旋向上（赝自旋向下）态的陈数，可推导出C±=±sgn（ζ）。KHANIKAEV A B 等在原胞内的圆柱中填充具有双各向异性响应的分裂环谐振腔［图2（a）］。这种超结构的双各向异性响应由本构关系描述：D=ϵ̂E+iχ̂H和B=μ̂H-iχ̂TE，其中χ̂是双各向异性张量。利用这种引入的非零双各向异性，将四重简并狄拉克点打开，最终得到一个具有非零自旋陈数的拓扑光子晶体。随后将拓扑平庸和非平庸的光子晶体拼接在一起，模拟得到拓扑保护的边界态，且对大转角传输有较强的抗散射性［图2（b）］。作为在光子系统中实现类量子自旋霍尔效应的早期工作，该工作使二维双各向异性光子晶体成为研究时间反演不变拓扑态基本物理的有力平台。

在自然界中，光学材料的双各向异性效应很弱，对自旋光子晶体的实验实现带来挑战。CHEN Wenjie等［23］利用单轴超构晶体波导获得了较大的等效双各向异性响应［图2（c）］，率先在实验上实现了自旋光子晶体并演示了边界态的抗散射传输。在超构晶体波导中，波导模式是自然耦合的，导致了等效的双各向异性响应，该响应与波导模式的阶数和波导厚度成正比。在实验样品中，他们设计了“陀螺形”和“星形”两种非共振、ε/μ匹配的单元结构，将它们排列成三角晶格，设计了光子拓扑绝缘体（Photonic Topological Insulator，PTI）和光子普通绝缘体（Photonic Ordinary Insulator，POI）。通过在PTI 和POI 之间形成一条边界，观察到了赝自旋极化的单向边界态。为了测试边界态的抗散射能力，他们在波导中引入了缺陷，用“陀螺形”单元代替了五个“星形”单元。虽然引入了缺陷，但Ez和Hz场仍维持了高透射率。

以上介绍的自旋光子晶体需要金属材料，由于金属在光学波段吸收较大，限制了其在更高频率下的应用。片上器件的应用与全介质设计方案更为兼容，为了实现这一点，WU Longhua 和HU Xiao 证明，具有晶体对称性的全介质PC 也可以实现类量子自旋霍尔效应［26］。他们通过将三角形晶格原胞中每个圆柱变为六个围绕中心均匀分布的圆柱，实现了类量子自旋霍尔效应［图2（d）］。在这种结构的光子晶体中，点K/K′处的狄拉克锥折叠到点Γ处，形成双重简并狄拉克锥。在这种C6v对称的光子晶体中，波函数角动量的正负充当了赝自旋的角色。通过求解麦克斯韦方程组，得到了简并的类轨道p 波和d 波本征场。通过收缩或扩大六角形圆柱簇，打开了双重简并狄拉克锥，获得了两个拓扑上不同的带隙［图2（d）］。等效哈密顿量可以体现出能带结构的演化和相关的拓扑相变为

图2 由双各向异性材料或全介质材料实现的自旋光子晶体Fig.2 Quantum spin Hall PC realized by bianisotropic materials or all-dielectric materials

它与Bernevig-Hughes-Zhang 模型的哈密顿量有相似的形式［33］。表征赝自旋向上和赝自旋向下的自旋陈数可以计算为C±=±［sgn（M）+sgn（-B）］/2。由于参数B通常为负，当参数M的符号为正时，自旋陈数将不为零。

上述光子晶体设计简单，是一种很有前途的光子应用平台。随后，DENG Weimin 等利用TE 偏振的全介质光子晶体实现类量子自旋霍尔效应，并揭示了其中存在的相位涡旋［27］。他们发现赝自旋极化的边界态携带相位涡旋，同时发现沿相反方向传输的边界态中相位涡旋的拓扑荷互为相反数。利用这一特性，他们证明可以用携带相反拓扑荷的相位涡旋激发源实现边界态的单向激发。YANG Yuting 等在微波段通过Al2O3圆柱周期排列也实现了这种自旋光子晶体，如图4（e）所示［29］。他们在拓扑光子晶体和普通光子晶体之间建立了一个大角度转弯界面，观察了赝自旋偏振边界态的传输。此外，他们设计了一个方形四天线阵列，利用相位涡旋-赝自旋极化锁定，选择性地激发了两种赝自旋偏振态，且在实验中观测到了拓扑边界态的单向激发。与基于金属材料的光子晶体相比，采用介质柱的C6v对称点阵结构简单，对集成光学器件更为友好，但在实际应用中仍存在一些困难。例如，为了抑制光子晶体的面外辐射，往往采用金属反射镜。BARIK S 等提出了一种具有类TE 模式带隙的悬浮硅光子晶体平板［30］，该方案可以一定程度上抑制面外辐射且没有金属成分。2018 年，他们在实验上展示了这种结构的拓扑特性，如赝自旋-路径锁定和抗散射传输［28］。这种纳米结构硅板构成了探索具有拓扑保护的多体量子物理的平台。近年来，自旋光子晶体的工作波长已达到了可见光波段。PENG Siying 等对三角格子的硅基圆柱进行了实验测量［31］，制作了周期性蜂窝纳米柱［图2（f）］。通过绘制深亚波长分辨率的局域光密度图，测量了可见光谱范围内的体能带。该工作所提供的硅基拓扑光子结构有望用于可见波段的平面硅基集成光子技术。

1.3 基于类量子能谷霍尔效应的拓扑光子晶体

自旋光子晶体是一种时间反演不变系统，有利于在光学频率领域的进一步应用，然而其光子能带工作于光锥以上，面外辐射损耗的抑制依然具有较大的难度。最近，光子晶体的另一个自由度“能谷”被开发，出现了基于类量子能谷霍尔效应的拓扑光子晶体，称为能谷光子晶体（Valley Photonic Crystals，VPC）。能谷光子晶体的能带工作于光锥以下，是实现具备低面外辐射损耗的拓扑光子结构的可靠方案。自提出以来，能谷光子晶体受到了人们的广泛研究［9，24，34-49］。2016 年，MA T 和SHVETS G 研究了全硅介质光子晶体中的类量子能谷霍尔效应［35］。C6v对称的光子晶体由于对称性在K点处出现必然简并，即狄拉克点，当空间反演对称性被破坏时，狄拉克点被打开，TE 模式体带中出现一个完整的带隙［图3（a）］。等效哈密顿量的形式为式中，σ̂i和τ̂i是泡利矩阵，作用于二重狄拉克简并和能谷的子空间。最后一项打开了宽度为2|λ|的带隙。拓扑指数CK/K′定义为接近K/K′的半布里渊区的贝里曲率的积分，能谷陈数CV=CK-CK′。λ的符号决定了能谷陈数，CV=sgn（λ）。由此得到的非0 能谷陈数表示非平庸拓扑。由两个具有相反能谷陈数的光子晶体构成的边界支持拓扑边界态，这种边界态能够大角度转弯保持抗散射传输［图3（b）］。

图3 能谷光子晶体的能带和边界模式，及其在各种波段下的实验实现Fig.3 Band structure and edge states of VPCs，and experimental realization of VPCs in various bands

同时期，DONG Jianwen、CHEN Xiaodong 等分别开展了基于类量子能谷霍尔效应的拓扑光子晶体系列工作，正式提出了“能谷光子晶体”概念［36，37］。DONG Jianwen 等设计了具有能谷依赖自旋分裂体带能带的能谷光子晶体［36］。通过使一个原胞中的两根介质柱具有相反的双各向异性，打破了空间反演对称性。在陈数、自旋陈数和能谷陈数为零的情况下，观察到了光子的能谷霍尔效应。能谷自旋锁定行为表现为相反赝自旋的光流传向了不同的ΓK和ΓK′方向。由于能谷自旋锁定行为，选择LCP 或RCP 源可以选择性地激发纯净赝自旋光流。CHEN Xiaodong 等［37］讨论了能谷光子晶体中的能谷对比物理。他们考虑全介质蜂窝形光子晶体中的TM 波，揭示了体态中存在相位涡旋，并且K和K′能谷处体态携带的相位涡旋具有相反的拓扑荷。他们通过数值模拟证明了利用拓扑荷为1 和-1 的激发源可以分别激发K和K′能谷处的体态。同时他们计算了贝里曲率分布，发现其局限于点K和K′附近。通过Z 形弯曲边界的后向散射抑制传输［图3（b）］，展示了能谷依赖边界态及其宽带抗散射传输的能力。此后，多个研究小组在实验中观测到了能谷光子晶体中的相位涡旋。GAO Zhen 等设计了一种表面波能谷光子晶体，利用微波近场扫描技术在实验中直接观测到了能谷光子晶体中的相位涡旋［39］。YE Liping 和YANG Yuting 等在微波频段利用携带相位涡旋的激发源实现了对K和K′能谷处体态的选择性激发［40］。以上提到的工作中激发源的拓扑荷都是±1，从理论上来讲，相位涡旋的拓扑荷可以是任意整数，不仅仅局限于±1 这两种情况。DENG Weimin 等研究了激发源的拓扑荷从-1 逐渐增加到5 时能谷光子晶体体态的激发情况，证明了高阶相位涡旋激发源激发体态所满足的选择定则［41］。利用该选择定则，他们发现可以根据电场的傅里叶谱反推出激发源的拓扑荷。

随着越来越多的理论研究，能谷光子晶体边界态的实验实现变得至关重要［9，38-40，43-47］。研究人员们首先在微波波段进行了充分的实验研究。例如，WU Xiaoxiao 等直接观察到表面等离子体晶体中的能谷边界态［43］。如果打破镜面对称性，这种表面等离子晶体就变成了能谷霍尔光子拓扑绝缘体，并且支持拓扑边界态［图3（c）］。CHEN Xiaodong 等用陶瓷圆柱组成了能谷光子晶体［图3（d）］，并在微波波段实验观察到了边界态的抗散射传输［44］。

拓扑光子学有望在片上集成光子学中得到应用。随着绝缘层上硅（silicon-on-insulator，SOI）微纳加工技术的进步，使得在实验上实现了工作于近红外波段的能谷光子晶体成为可能［9，45］。SHALAEV M I 等［45］制造了一种实现类量子能谷霍尔效应的光学拓扑绝缘体［图3（e）］。通过改变原胞中两个三角形孔的大小，打破了镜像对称性。通过直通道和梯形通道的透射光谱测量，发现结构支持边界态的拓扑保护传输。HE Xintao 等［9］在SOI 能谷光子晶体平板中也实验观测了急弯抗散射拓扑传输，这种结构在近红外波段处有类TE 模式的带隙［图3（f）］。不仅如此，HE Xintao 等［9］还发现了边界态传播方向与体态相位涡旋方向之间的联系，即边界态的能谷关联传输，从而可以人为控制相位涡旋的方向来选择性激发不同传播方向的边界态；利用这种特性，他们在实验上实现了能谷关联光子路由行为。另一方面，太赫兹技术因其在下一代通信技术中的潜在应用而受到越来越多的关注。YANG Yihao 等［46］在全硅芯片上实现了在太赫兹工作的能谷光子晶体，且支持抗散射传输［图3（g）］。

2 拓扑光子晶体的应用

拓扑光子学在理论上被提出并在光子晶体上实验后，研究者们进一步探索了拓扑光子晶体的潜在应用。基于拓扑光子晶体诸多新颖的光场调控能力（例如抗散射性），人们提出了许多无源和有源光子器件的原型。

2.1 拓扑光子晶体的抗散射传输

抗散射性是拓扑光子晶体最重要的特性之一。对于二维拓扑光子晶体，其边界态的抗散射性允许电磁波在存在无序、缺陷或大转角转弯的情况下抑制后向散射传输。例如，在霍尔光子晶体［7，8，15-17，20］中，当外加电场或磁场时，可以获得稳定的单向手性边界态；如图4（a）所示，这些边界态是单向的，并且对障碍物具有鲁棒性［20］；即使在路径中放置金属散射体，边界态也不会出现后向散射。与霍尔光子晶体中手性边界态的抗散射性类似，当缺陷不引起两个赝自旋模式之间的耦合时，自旋光子晶体中的边界态对缺陷具有抗散射性［22，23，25，26，29-32］；例如，在图4（b）中，两种自旋陈数的拓扑光子晶体界面支持的边界态，表现出对大转弯、空腔、无序等缺陷的鲁棒传输［32］。许多工作也讨论了能谷光子晶体中能谷相关边界态的抗散射性［9，35，37，39，45，46］。HE Xintao 等展示了SOI 能谷光子晶体平板中的能谷依赖边界态［9］，在亚波长尺度上沿Z 形和Ω 形弯曲的通道中观察到了通信波段光信号的抗散射传输，展示出平顶高透射现象［图4（d）］。同样利用能谷光子晶体边界态的抗后向散射传输能力，GAO Fei 等［38］通过抑制边界态的能谷间散射，实现了边界态与均匀介质的完美耦合［图4（c）］。YANG Yihao 等［46］构造了一个片上能谷光子晶体波导，并利用它于太赫兹波段传输未压缩4K 视频的信息［图4（e）］；实验证明了4K 高清视频即使在高度扭曲的通道中也能通过能谷光子晶体波导实时传输且保持极低的误码率。CHEN Xiaodong 等［25］通过调整蜂巢形晶格中介质的介电常数张量，使得TE 模式和TM 模式的狄拉克点发生偶然简并，后引入双各向异性打破简并出现带隙，理论提出了自旋陈数依赖双各向异性参数符号的拓扑光子晶体。拼接自旋陈数相反的拓扑光子晶体，在边界处出现了对大转弯传输抗散射的边界模式［图4（f）］。除了对大角度转弯的后向散射抑制能力，能谷光子晶体还具有脉冲无畸变传输的能力。SHI Fulong 等［50］利用能谷光子晶体边界态的低群速度色散，实现了脉冲的无畸变传输。实验证明脉冲在通道中呈现匀速运动且不同位置的半高宽没有明显变化［图4（g）］。

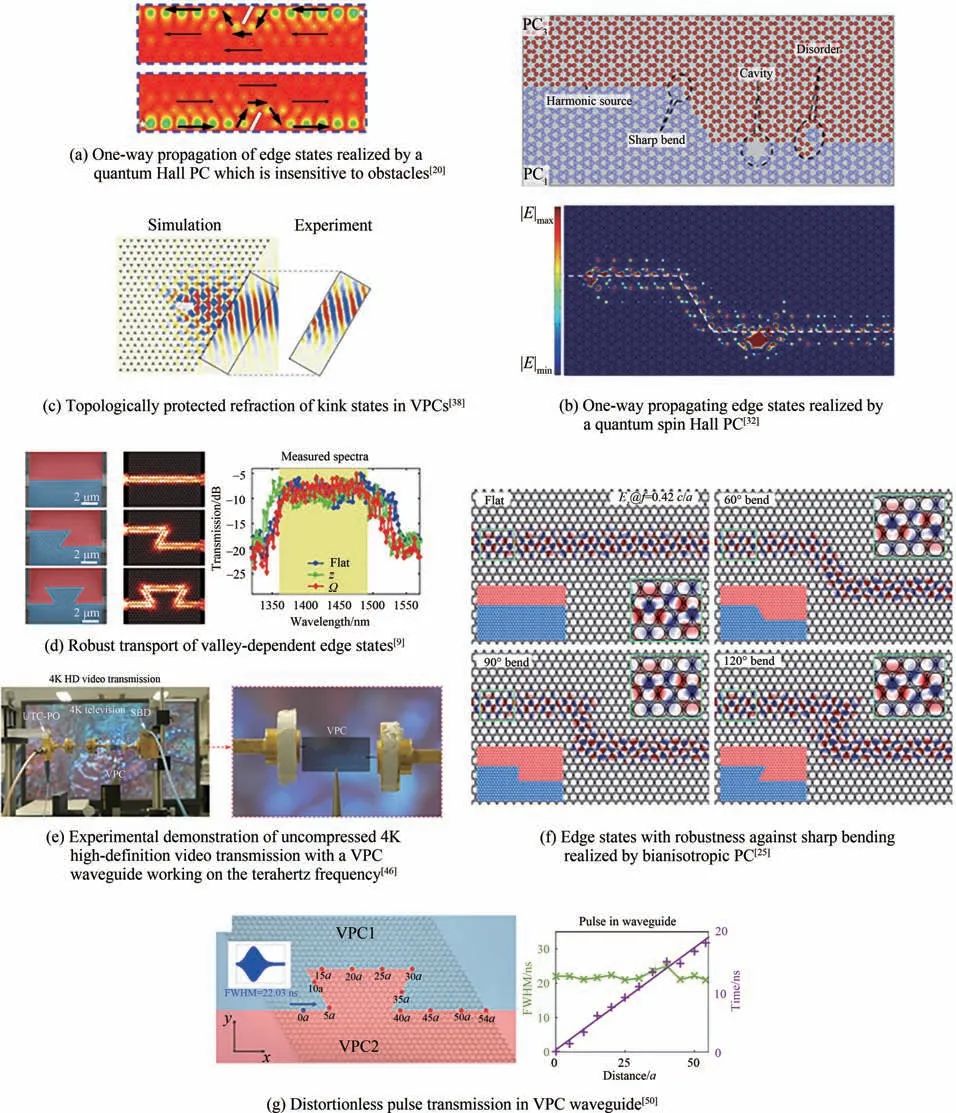
图4 由拓扑光子晶体实现的抗散射传输Fig.4 Anti scattering propagation realized by TPCs

2.2 拓扑光子晶体的无源器件

由于拓扑光子晶体在光场调控方面显示出了巨大的潜力，许多应用被提出并有望实现高性能的光学器件。路由器是光学集成线路的重要组成部分之一，它可以将信息引导到所需的方向。能谷光子晶体波导具有实现这一功能的潜力，利用它的能谷锁定传播模式，可以引导光的传播方向。利用能谷与相位涡旋的对应关系，HE Xintao 等提出了一种拓扑光子路由方案［9］。这种能谷光子晶体路由样品的结构如图5（a）所示，包括两条能谷光子晶体波导和一个亚波长微盘。当光从条形硅波导入射时，微盘中会产生顺时针或逆时针方向的相位涡旋。然后，具有不同相位旋涡的光根据手性耦合到不同能谷的边界态模式，它们具有不同的传播方向。除了利用能谷锁定传播，还可以同时利用能谷自由度和赝自旋自由度来实现光子路由［24，48］。图5（b）展示了由自旋光子晶体和能谷光子晶体共同组成的光子路由结构［48］。由于赝自旋边界态和能谷边界态不能互相耦合，它们只能沿各自的通道传输，实现光子路由。

在光通信中，波分复用是一种利用不同波长将多个光载波信号复用到单个光纤/波导上的技术。波分复用系统在发射端使用多路复用器将多个信号合并入一个通道，在接收端使用解复用器将它们分开。利用波导模式和微腔模式之间的耦合，可以在光子晶体平板上实现波分复用器和解复用器［53］。最近，TANG Guojing 等基于双带隙能谷光子晶体提出了一种频率依赖的光子路径选择效应［51］，在波分复用器中具有潜在的应用前景。他们设计了具有两个不同频率范围的带隙的能谷光子晶体，在两个带隙中发现了频率范围相关的边界态：如图5（c）所示，VPC1 和VPC2 之间的通道支持两个带隙的边界态，VPC3 和VPC2 之间的通道只支持第一带隙的边界态，而VPC1 和VPC3 之间的信道只支持第二带隙的边界态。因此，位于不同带隙中的边界态将沿着不同的路径传播并在路径上分离。

分束器是将一束光一分为二的光学装置。它是干涉仪等光学测量系统的重要组成部分，在光通信中有着广泛的应用。通过设计波导的拓扑结构或接口，人们提出了几种由光子晶体制成的分束器［54，55］。2021 年，CHEN Yang 与HE Xintao 等基于能谷光子晶体的急弯波导设计了鱼叉型片上分束器［13］。如图5（d）所示，由于能谷光子晶体的能谷依赖边界态的相位涡旋和选择性耦合，上方入射的光信号只向前后传输，不会向下通道传输，实现光信号的等分传输，并进行了拓扑保护光量子干涉实验演示。

光学谐振腔在物理和工程领域有着广泛的应用，包括相干电子-光子相互作用、低阈值激光、非线性光学等。由金属制成的腔体在高频段下会产生吸收损耗，因此很难在集成系统中使用。相比之下，由介电材料制成的光子晶体等全介质超结构能够为集成光谐振腔设计带来更多的可能性。利用光子晶体中的缺陷模式，研究人员提出了光学波长尺寸的高Q 纳米腔［56］。而拓扑结构的引入为谐振腔的设计带来了新的机制，研究人员在拓扑光子晶体中使用抗散射边界模式，提出了光沿着边界传播的微腔［16，57，58］，并且边界模式不易受到传输通道缺陷的影响。利用能谷光子晶体边界模式的单向传输，也可以实现光子微腔。例如，2020 年LI Yandong 等提出了一种基于能谷光子晶体中能谷自由度近似守恒的新型光子谐振腔［52］。当不存在能谷翻转扰动时，能谷相关模式将单向传播。因此，如图5（e）所示，当在能谷光子晶体波导的末端放置理想电导体时，光不会向后反射，且设定其频率处于光子晶体与理想电导体边界模式的禁带中，导致光局域于末端，实现光子微腔。此外，基于实空间拓扑［59］、扎克相位［60］、Jackiw-Rebbi 模型［61］、狄拉克涡旋拓扑［62］和最近的高阶拓扑［63，64］的几种拓扑光学微腔也被提出。

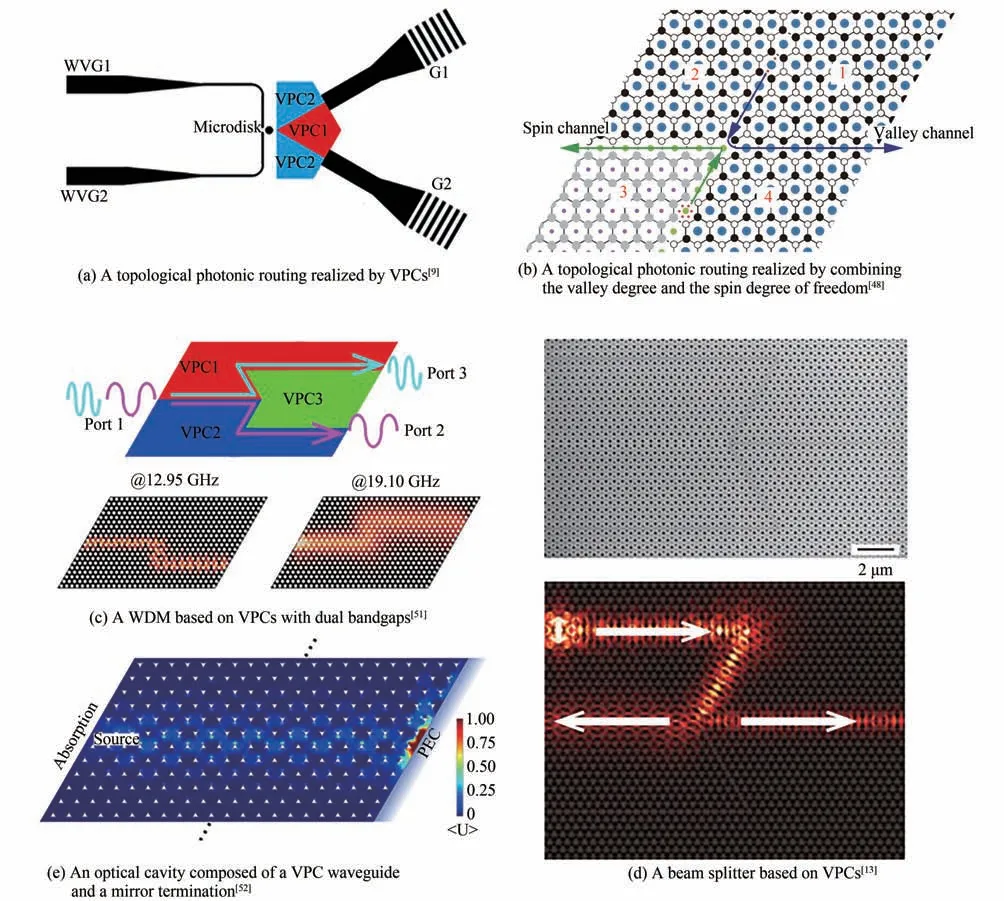
图5 由拓扑光子晶体实现的无源器件Fig.5 Passive devices realized by TPCs

2.3 拓扑光子晶体的可重构和有源器件

基于拓扑光子晶体波导新颖的传输特性，人们设计了多种高性能的光学元件。但上述结构或组件只能在固定波长范围内工作，不能主动调谐。对于许多光器件如调制器、开关和光缓冲器，可调谐性很重要且富有应用前景。可重构的拓扑光学器件是光学集成线路中必不可少的器件。为了克服这一挑战，研究人员提出了一些可重构拓扑光子晶体系统［42，65，66］。一种动态调谐拓扑光子晶体模式的方法，是通过光泵浦、电泵浦等常用手段改变光子晶体或背景材料的介电常数或磁导率来实现的。如SHALAEV M I 等利用硅的自由载流子光激发，通过紫外光束泵浦能谷光子晶体来调制其折射率［65］，折射率的变化导致了能带结构的变化及带隙的位置改变［图6（a）］。利用这种动态控制，有望实现开关时间为纳秒级的全光开关。除了利用泵浦光主动控制拓扑光子晶体系统外，还可以利用光电材料施加外部电场来调控。例如，图6（b）显示了由TiO2和电光材料BaTiO3组成的能谷光子晶体［42］。这种光子晶体平板嵌入SiO2层，夹在两层金薄膜之间。通过控制两电极之间的电压，即两层金薄膜，可以改变BaTiO3的折射率，从而动态改变了空间反演对称性的强度。结果表明能谷光子晶体的拓扑相可以随外加电压动态控制，再由于边界态的相位涡旋-能谷锁定，同一激发源产生的边界态会在不同外加电压中具有不同的传播方向，实现光开关。

图6 由拓扑光子晶体实现的有源器件和光量子器件Fig.6 Active devices and optics quantum devices realized by TPCs

片上光源是集成光子线路中重要的光学元件，可用于通信、信号处理、成像和传感等领域。能谷边界态的抗散射和手性使能谷霍尔拓扑激光器成为一种很有前景的器件［57，58］。借助能谷锁定传播模式，能谷光子晶体可以实现手征拓扑谐振腔［57］。能谷光子晶体谐振腔的示意图如图6（c）中插图所示。以量子点为激励源，用激光泵浦，激发了谐振模式。探测位置设置在谐振腔的三个侧面，图6（c）显示了相应的测量光谱。频谱分析表明，能谷光子晶体谐振腔支持三种谐振模式，且具有相似的强度分布，表明了能谷光子晶体谐振腔的抗散射特性。

2.4 拓扑光量子器件

最近，人们开始将拓扑光子学引入量子光学，从而实现拓扑保护的光量子行为［10-13，28，57］。2018 年，BARIK S 等基于拓扑光子晶体设计了单量子发射器和拓扑光子态之间的界面［28］。如图6（d）所示，单量子发射器有效地耦合到两个拓扑相不同的全介质光子晶体边界处的拓扑边界态。实验展示了拓扑边界态的手性性质。在面外方向施加磁场时，单量子发射器会产生塞曼分裂，激发态分裂成两个具有相反圆偏振的非简并态。这两个相反的圆偏振态沿波导的传播方向不同。实验证明拓扑边界态对通道弯曲具有鲁棒性。根据二阶相关测量结果，确定了路由光子为单光子。2021 年，CHEN Yang 和HE Xintao 等［13］将拓扑光子学和量子光学相结合，实现了片上能谷依赖的量子信息过程。他们基于能谷光子晶体的急弯波导设计和制造了鱼叉型片上分束器，并使用该器件实现了高可见度的双光子干涉［图6（e）］。该工作首次证明了能谷拓扑光子态可以用于光量子信息处理，而且有望实现更复杂的光量子电路，这为片上光量子信息处理提供了一种新的方法。

3 总结与展望

本文回顾了拓扑光子晶体的物理特性、设计方法和器件应用。首先，简述了基于类量子霍尔、类量子自旋霍尔、类量子能谷霍尔效应等类量子效应光子晶体的基本原理，并介绍了一些具体的工作中的设计思路和实验结果。然后，介绍了拓扑光子晶体在无源器件（如波导、谐振腔、光路由、分光器、波分复用器等器件）的潜在应用，以及在有源器件（如光开关、激光和光量子器件等器件）的潜在应用。

在微波领域的理论探索和实验实现的基础上，光学波段的拓扑光学片上现象演示和器件原型越来越多。支持全介质设计、与CMOS 工艺兼容的拓扑光子系统有望在实际的光子器件中得到应用。同时，集成光子学器件中的插入损耗和面外辐射等问题将是不可避免的挑战。由于因插入损耗和面外辐射带来的较高传输损耗，比起抗散射性传输，拓扑光子晶体器件的优势更体现于复杂光场调控能力和高制造容差等特性。充分利用拓扑光学理论引入所带来的优势，在特定功能上实现传统光学器件无法实现的拓扑光子学器件，是较为重要的研究方向。

探索新颖的拓扑物理是重要的研究方向，而光子晶体和超构表面等超结构是探索和实现拓扑物理现象的便捷平台。在理论方面，拓扑光子学可以很好地补足传统光学理论在分析超结构中光传输行为的不足之处；在应用方面，大量基于拓扑光子学设计的超结构展示出了良好的性能指标，体现了其在微纳集成光子与光量子器件中的潜在应用。由此可见，无论在光学原理方面还是在实际应用方面，拓扑光子学都是超构光子学的一个重要分支。本文主要介绍了拓扑光子晶体及其基于拓扑效应实现的抗散射光传输行为和各种功能的有源或无源光子与光量子器件。

另一方面，随着光学器件越来越高的集成化与微型化需求，作为超构光子学的另一分支，超构表面由于其设计自由度高、调控精度高和超薄超轻的特性，也受到了研究者的广泛关注。例如，在超构表面透镜与微光学成像方面有许多创新性成果，包括但不限于高数值孔径与高效率的亚波长薄透镜［67］、可实现可见光衍射极限聚焦和亚波长分辨率成像的超构透镜［68］、由超透镜阵列实现的多光子量子光源［69］、高数值孔径且厘米尺寸的超构透镜［70］、全可见光宽带消色差超构透镜阵列的3D 成像方案［71］、微型化的宽视场亚微米级分辨率的级联超构物镜［72］等。同时，借助拓扑光子学，不少研究面外光场调控的拓扑超构表面工作也被提出，如利用非厄米拓扑理论中的Exceptional point（EP 点）理论设计的拓扑超表面，可以实现将左/右旋光向不同方向反射［73］，或是将左/右旋光转换为右/左旋光［74］。以上成果在VR/AR、三维显示、生物医学显微检测等领域具有广泛的应用前景。

超构光子学基于人工结构的设计实现多维度光场调控，因其结构的多样性丰富了光物理与光应用。在拓扑光学、量子光学、非线性光学等基础物理研究中催生了一系列物理现象与原理的发现，推动了包括拓扑光子晶体、超构表面、光量子调控、非线性光学效应在内等前沿科学领域的发展。同时，这也将在新一代信息技术中发挥着至关重要的作用。依托超构光子学原理开发的微光学器件与系统，近年来逐渐在包括光子集成电路、显微成像、近眼显示、光量子计算、量子精密测量等国家关键科技领域展现出巨大的应用潜力，成为备受瞩目的变革性技术。未来，随着超构光子学的发展，超结构在光物理与光应用的深入研究将为军事、医疗、显示等军民行业带来一系列不可或缺的关键技术。