预应力混凝土连续箱梁桥LCPA法剩余使用寿命预测*
2022-06-27王继林夏叶飞袁微微宗周红
王继林 夏叶飞 袁微微 宗周红
(1.华设设计集团股份有限公司 南京 210014; 2.东南大学土木工程学院 南京 210096)
为了保障桥梁交通的安全畅通,迫切要求对既有桥梁全面评价全寿命周期技术性能。剩余使用寿命预测研究是一个复杂的课题,尽管已有大量学者开展理论实践研究,但依然存在许多值得探讨和研究的问题。如在桥梁体系的可靠度分析中,构件层次已经作了尝试研究,但在结构体系可靠性研究方面还需进一步深入。国内外众多学者对在役混凝土结构抗力影响因素方面进行了大量的理论和试验研究,目前建筑结构方面的研究成果较多,而桥梁结构方面研究成果很少。现今研究者多从考虑桥梁全寿命期内的耐久性能或安全性能来进行桥梁分析研究,较少综合考虑耐久性能和安全性能。
本文综合考虑结构服役寿命周期内桥梁实际耐久性能和安全性能,进行结构服役全寿命周期性能预测评估[1](life cycle performance assessment,LCPA),先计算结构功能函数时变可靠度,通过可接受可靠度界限进行桥梁剩余使用寿命预测研究。桥梁LCPA剩余使用寿命预测是在考虑寿命期荷载和耐久性因素对结构的极限承载力指标和正常使用状态功能可靠度影响的基础上,实现寿命预测。
1 桥梁LCPA剩余使用寿命预测内容
结构全周期寿命是指桥梁从交竣工验收至结构状况退化到临界危险水平的服役时间,桥梁服役期根据实际作用和结构损伤实时预测结构可靠度可以预测桥梁剩余的使用寿命。预测的剩余使用寿命与众多因素有关,如材料性能、结构形式、劣化机理、维修方式等。通常混凝土桥梁的劣化是诸多因素共同作用的结果,现今还是无法全面地量化这些影响因素。本文尝试通过随机过程的方法综合考虑结构安全性能与耐久性能,通过同时考虑安全性和耐久性来进行桥梁剩余使用寿命的预测。
对结构进行LCPA剩余使用寿命预测,需先进行结构各要素时变可靠度的研究。当前各类时变可靠度领域发展迅速,这些成果为预测结构剩余使用寿命理论奠定了坚实的基础。2011年Frangopol、Tong Guo等针对现存的预应力混凝土箱梁桥承受不断增加的交通荷载和处于恶劣环境下两方面问题,提出了多峰车载模型及箱梁桥的时变腐蚀模型,得出针对预应力混凝土箱梁桥的时变可靠度分析方法。
本项目以京沪高速(G2)新沂河大桥为工程背景,对连续梁桥进行LCPA剩余使用寿命的预测。主要步骤:①根据动态称重系统和统计分析,研究车辆荷载效应的时变可靠度模型,采用概率分布函数卷积的计算方法,研究总荷载效应最大值概率分布模型。②根据材料退化模型计算新沂河大桥的安全性和耐久性时变可靠度模型,依据LCPA对新沂河大桥进行剩余使用寿命预测。
2 LCPA剩余使用寿命预测
新沂河大桥位于京沪(G2)高速公路,跨越新沂河,桥梁上部结构采用30 m跨径先简支后连续的装配式部分预应力混凝土连续箱梁桥。2001年建成通车,2012年桥梁健康监测系统安装完成开始采集数据。本文以新沂河大桥状态识别研究为工程背景,立足于长期性能监测系统及动态称重系统,对连续梁桥进行LCPA剩余使用寿命的预测。本研究中主要是预测新沂河大桥的功能时变可靠度,结合目标可靠度指标对新沂河大桥的剩余使用寿命进行评估。主要内容如下:①依据动态称重系统数据得出既有桥梁的随机车载模型,结合恒载概率模型建立既有桥梁的荷载概率模型;②考虑构件耐久性参数随时间变化建立既有桥梁构件的抗力衰减概率模型;③计算箱梁抗力与效应包络时变可靠度,根据既有桥梁目标可靠度指标,预测评估既有桥梁的剩余使用寿命。
2.1 新沂河大桥荷载效应模型
2.1.1恒载效应概率模型
一般认为桥梁结构的恒载服从正态分布,恒载效应与恒载之间一般按线性关系考虑,恒载效应与恒载相同的概率模型,均满足正态分布,恒载弯矩效应概率分布函数FSG(x)和统计参数如式(1)、式(2)。
(1)
μSG=κSGSGK;σSG=μSGδSG
(2)
式中:SGK为单梁恒载弯矩效应标准值,SGK=3 434 kN·m;κSG=1.014 8;μSG、σSG、δSG分别为构件恒载效应的平均值、标准差和变异系数,μSG=3 485 kN·m,σSG=150 kN·m,δSG=0.043 1。
2.1.2车辆活载效应概率模型
新沂河大桥实际运行车辆荷载为一般运行状态与密集运行状态的综合,称为混合运行状态。按照2种运行状态下各自车队总数的比例,将一般与密集运行状态下的弯矩概率函数进行组合,得到混合运行状态下的概率密度函数,进而得到荷载重现期分别为1,5,10,30,50,70,100年时的混合状态下的弯矩概率分布函数。下面采用2013年4月份-2014年4月份动态称重系统采集的活载数据,取重现期1年,计算混合运行状态下1年梁体跨中截面活载弯矩效用最大值的概率分布函数F1年(M)[2],概率分布函数见图1。
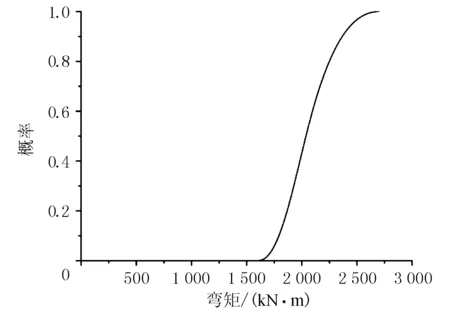
图1 1年重现期车辆活载弯距效应概率F1年(M)分布图
2.2 新沂河大桥抗力概率模型
通常假定构件抗力概率分布服从对数正态分布,在役桥梁构件的弯矩抗力衰减概率模型可按式(3)计算。
R(t)=KT(t)KP(t)RP[fcd(t),fsd(t),
δel(t),ky(t),kb(t)…]
(3)
式中:R(t)为构件抗力随机过程模型;KT(t)为考虑抗力参数测试及预测影响的随机变量;Kp(t)为抗力计算模式不定性随机变量;Rp(·)为规范中的抗力计算公式;fcd(t)、fsd(t)为材料强度退化随机值;δel(t)、ky(t)、kb(t)为第i根钢筋锈蚀深度屈服强度协同工作系数预测值。JTG 3362-2018规范中,箱梁正截面受弯抗力预测概率模型如式(4)。
(4)

具体在推导构件抗力预测概率模型时需要综合考虑混凝土的强度、钢筋锈蚀深度、钢筋黏结性能等耐久因素退化。本项目工程桥梁处于江苏淮安沭阳地区,相应参数时变模型选择牛荻涛[3]模型,包括混凝土强度经时变化模型、钢筋锈蚀率模型等。
1) 一般大气环境下混凝土强度劣化模型、混凝土强度经时变化模型,混凝土强度平均值μf(t)和标准差σf(t)的经时模型如式(5)。
(5)
式中:μf0为混凝土强度回弹实测推定值,本桥取21.7 MPa;η(t)为混凝土强度平均值随时间变化的函数;σf0为混凝土强度回弹实测换算值标准差,本桥取1.05 MPa。
2) 钢筋锈蚀深度(保护层胀裂前)计算采用牛荻涛[4]锈蚀深度预测模型如式(6)。
(6)
式中:δel(t)为混凝土保护层的钢筋锈蚀深度,mm;λel为锈胀开裂前的钢筋锈蚀速度,mm/年;kcr为钢筋位置修正系数;kce为环境条件修正系数;RH为环境相对湿度,%;d为混凝土保护层厚度,mm;fcu为混凝土立方体抗压强度,MPa。
3) 计算锈蚀钢筋屈服强度降低系数ky(t),屈服强度降低系数的计算采用惠云玲[5]模型,如式(7)。
(7)
式中:ηs(t)为钢筋锈损率;δe(t)为钢筋锈蚀深度,mm;D为钢筋直径,mm。
4) 锈蚀钢筋与混凝土协同工作系数kb(t)计算采用金伟良[6]模型如式(8)。
kp(t)=
(8)
2.3 连续梁桥LCPA法剩余使用寿命预测
桥梁结构的目标可靠指标受破坏影响程度、评估基准期、构件对结构整体安全的影响程度、结构的重要性等因素影响,目标可靠指标见表1。根据实际结构破坏类型特征,本次参照文献[7-8]将0.85%作为结构达到寿命终点标志,取新沂河大桥目标可靠指标3.995,对应目标失效概率为1.1×10-6。应用新沂河大桥荷载效应概率模型及抗力衰减概率模型,依据JC法及Monte-Carlo法计算新沂河大桥的弯矩时变可靠指标,依据目标可靠指标预测新沂河大桥的剩余使用寿命。

表1 结构破坏类型对应的折减目标可靠指标0.85β0和目标失效概率
2.3.1JC法计算结构可靠指标
设结构功能函数Z为随机自变量Xi(i=1,2…n)的函数,Z=g(x1,x2,…,xn)=R(x1,x2,…xn)-S(x1,x2,…,xn)。结构可靠度即为求函数Z可靠度。为避免中心点法中的误差,本文提出了验算点法计算函数可靠度。验算点法是将线性化点选在功能函数Z=0且为最大失效概率对应点(x1*,x2*,…,xn*)上,在P*点上用Taylor级数线性化展开函数求解结构的可靠指标β值,该方法被国际安全度委员会(JCSS)所推荐,简称为JC法。根据上述原理将功能函数用Taylor级数在P*点上展开,取一阶项得功能函数Z均值和标准差。
则函数Z可靠指标β计算方法如式(9)。
(9)
根据新沂河大桥的监测数据统计规律,交通量年增长按1%预测,可得出评估期内每年的总荷(活)载效应分布,评估期内的结构抗力概率分布由式(9)计算,得出新沂河大桥函数Z时变可靠指标β。JC法计算结果见表2和图2,由此可知2021年新沂河大桥的时变可靠指标降至4,而2022年时可靠指标降至3.9,小于目标可靠指标3.995。因此,从2012年JC法预测新沂河大桥剩余使用寿命为10年。
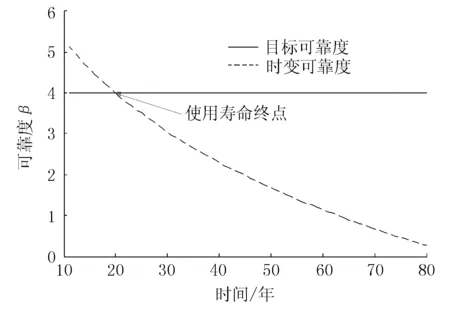
图2 JC法预测结构寿命可靠度曲线(2012年对应x=11)

表2 JC法预测结构安全可靠指标
2.3.2Monte-Carlo法计算结构失效概率
Monte-carlo法又称统计试验法,它是利用计算机进行大量抽样模拟随机变量的分布,反复进行试验观测取得服从相应分布的随机变量的子样,用子样的统计特征近似代表随机变量母体的统计特征,进而估计结构体系的失效概率pf。新沂河大桥目标失效概率为1.1×10-6,Monte-Carlo法计算结果见表3。由表3可知,2019年新沂河大桥的时变失效概率值达到6.3×10-6,首次超越目标失效概率。因此,通过Monte-Carlo法计算新沂河大桥剩余使用寿命为8年。

表3 Monte-Carlo法预测结构失效概率pf数据
2.3.3预测剩余寿命数据验证
对于新沂河大桥来说,JC法计算结果可作为Monte-Carlo法预测的剩余使用寿命结果的参考。JC法验证Monte-Carlo法预测剩余使用寿命结果是否可靠。JC法预测得出的新沂河大桥剩余使用寿命为10年,Monte-Carlo法预测得出的剩余使用寿命为8年,两者结果较为接近。剩余寿命预测数据表明新沂河大桥技术状况较差。
2013年6月利用在线监测系统进行静载试验数据分析。新沂河大桥右幅第九联中跨箱梁当加载至4级,相当于汽车超-20级荷载等级时,测试截面箱梁位移和应变均存在实测值大于理论值的现象,并出现箱梁裂缝大量增加和裂缝宽度大幅增大现象。试验表明,新沂河大桥相应结构强度、刚度和抗裂性能不能满足汽车超-20级荷载等级的使用要求。
3 结论与展望
3.1 结论
1) 本项目立足于安全性和耐久性角度计算LCPA时变可靠度,采用JC法预测新沂河大桥剩余使用寿命为10年,采用Monte-Carlo法预测剩余使用寿命为8年,2种方法寿命预测结果较为接近。
2) 本项目建立了混凝土梁桥LCPA剩余使用寿命的预测流程和公式,结合项目实际应用了荷载效应模型及结构抗力模型进行可靠度评估,可为同类桥梁的剩余使用寿命预测提供参考。
3) 本次LCPA剩余使用寿命预测结果与实桥荷载试验结果一致,2种不同评估结果均表明新沂河大桥劣化程度加剧,不满足现行荷载的需求,需要及时进行维修加固。
3.2 展望
目前桥梁LCPA剩余使用寿命预测养护需求强烈,但研究还在发展中,尚有一些问题待进一步研究深化。
1) 本次LCPA桥梁剩余使用寿命预测方法仅考虑了结构抗弯性能,可能的情况下还应考虑抗剪、抗扭等其他承载力性能指标。
2) 桥梁耐久性能劣化模型和车辆荷载(活载)效应模型可分别从长期监(检)测和动态称重系统来进行优化,进一步提高综合耐久性和安全性桥梁LCPA剩余使用寿命预测方法的精度。
3) 本次LCPA桥梁剩余使用寿命预测仍然基于规范静态抗力和静态作用效应力演变规律。后期还可以进一步研究桥梁LCPA剩余使用寿命的动态预测方法,例如基于神经网络算法、灰色系统模型、人工智能系统等各种预测方法。
