顶部开口对起火房间热释放速率影响的数值模拟

刘 杨，张红伟，李 强

1.内蒙古自治区消防救援总队，内蒙古 呼和浩特 010070； 2.沧州市消防救援支队，河北 沧州 061000；3.中国人民警察大学 教务处，河北 廊坊 065000

0 引言

当起火房间存在顶部开口时，顶部开口与侧壁开口相互耦合会对起火空间的气体流动规律产生影响，进而影响火灾发展进程。与仅有侧壁开口起火房间采用中性面分析气体流动模式不同，顶部开口流动模式更为复杂[3]。研究表明，顶部开口流动模式与开口厚度(L)和开口直径(D)的比值相关。通过模拟试验研究，Mercer等发现L/D在3.5～18时，顶部开口的交换流量随着L/D的增大反而减小[4]。Epstein用Froude数表示交换流量，并给出4个Froude数与L/D的经验公式，以及单向溢出流流率的经验公式[5]，奠定了水平开口流动研究的基础。Cooper采用压力和浮力驱动相结合的分析模型，发现冷热气体的无量纲交换量接近一个常数[6]。Wakatsuki进行顶部开口腔室内乙醇油火试验研究，随着开口变化观察到三种火灾状态：缺氧自熄、不稳定脉动和稳定燃烧[7]。

顶部开口流动模式的复杂变化规律会与侧壁开口流动相互作用，使得揭示此类受限空间火灾发展规律非常复杂。随着人们对居住和使用环境舒适性的不断追求，天窗等顶部开口结构广泛应用于建筑空间。建筑空间作为一种独特的受限空间，其火灾研究的边界条件具有一定应用价值。如：顶部开口厚度远小于开口直径，侧壁开口高度和宽度相同，火场温度一般在200～1 000 ℃等，均利于揭示顶部开口对室内火灾发展的影响规律。本文对同时具有顶部和侧壁开口起火房间的热释放速率进行研究，为建筑空间消防工程设计提供依据。

1 模型建立与场景设计

1.1 FDS软件

火灾动力学模拟工具FDS是采用数值方法求解一组描述热驱动的低速流动Navier-Stokes方程的计算模型，可用于计算火灾烟气流动和热传递过程。对于本文所涉及的同时具有顶部和侧壁开口起火房间，其发展过程主要受控于开口流体流动的影响，适于采用FDS进行研究。

1.2 模型建立

同时具有顶部和侧壁开口房间模型如图1所示，其内尺寸为2.5 m×1.6 m×1.7 m，4个侧壁和顶部壁厚均为0.1 m，材料导热性设为绝热。侧壁开口靠底部居中设置在1.6 m×1.7 m一侧壁面，在房间顶部中央处设置一正方形水平开口。火源为边长0.4 m的正方形，设置在侧壁开口对面的地面中心线，一侧贴邻侧壁。温度测点设置在侧壁开口与顶部开口边缘的中心线。

图1 房间模型示意图

1.3 独立性分析

FDS模拟结果的准确性受网格数影响。通常情况下，网格数越多计算结果越准确，但其运行所需时间也会大幅增加。因此，在考虑计算结果精确性的同时必须考虑计算机运行能力。本文采用折中方法，选取不同比例网格，考察其测量结果，如果两种网格运行结果相近，数据收敛基本一致，则可认为所选网格合适。如表1所示，采用特征火焰尺寸的1/8～1/12进行网格独立性分析，火源选择热释放速率1 800 kW·m-2、燃烧面积0.25 m2的固体，侧壁开口尺寸为0.6 m×0.6 m。由不同网格尺寸下温度变化情况可知，场景MESH5的网格相比场景MESH1的网格较为精细，其模拟结果更具有代表性。因此，选定场景MESH5对应的网格作为模拟网格设定。

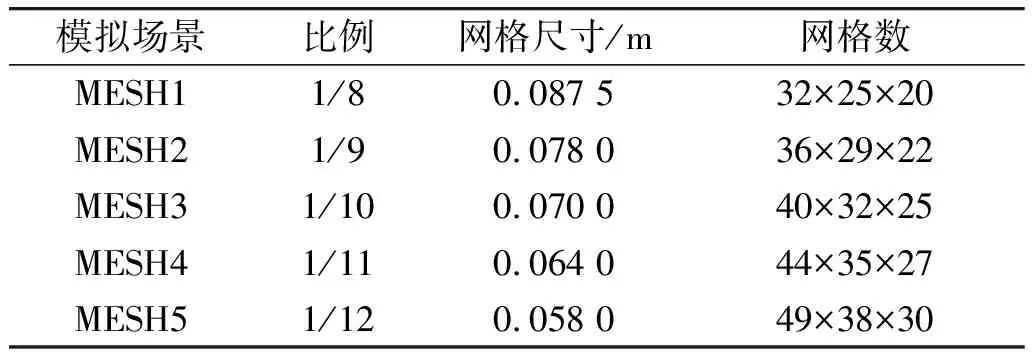
表1 独立性分析网格设置

1.4 场景设计

火源位置、开口位置见图1，火源热释放速率设为恒定值426 kW·m-2。为研究顶部开口与侧壁开口的耦合影响关系，选取不同开口尺寸设定模拟场景，如表2所示。

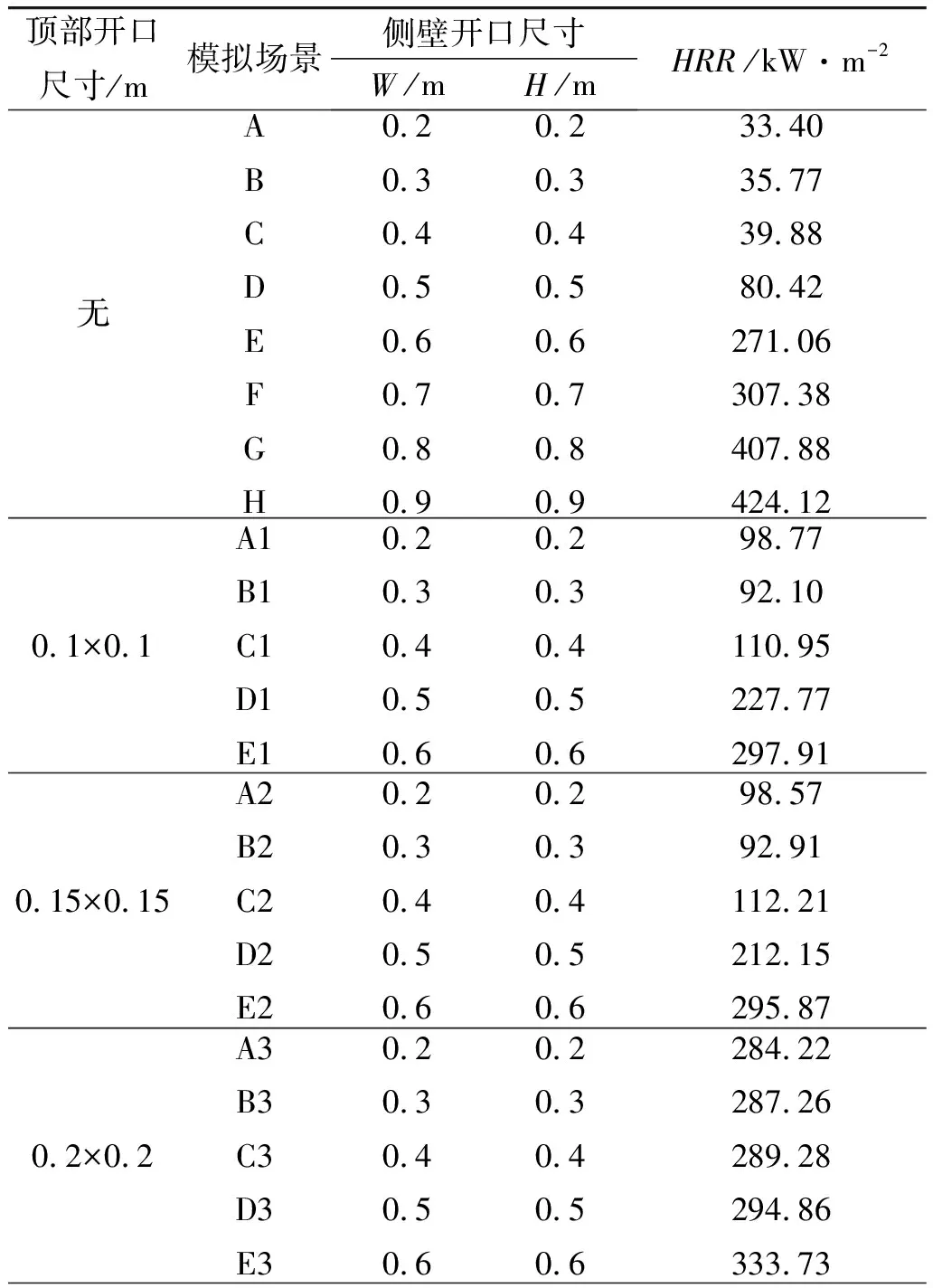
表2 模拟场景及热释放速率

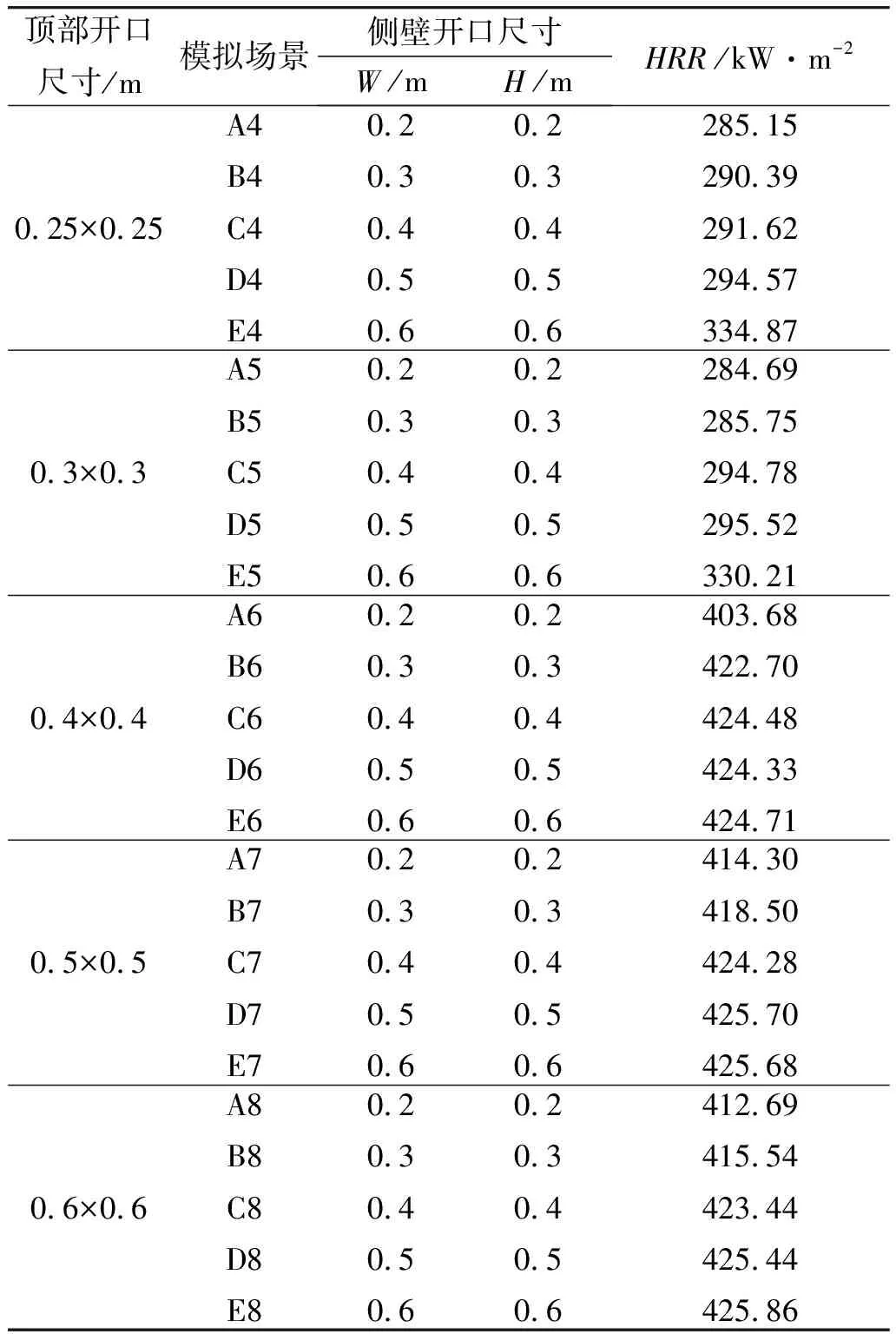
表2(续)

2 模拟结果与分析

2.1 无顶部开口场景

从图2可以看出，对于无顶部开口场景，热释放速率呈现出两种不同变化规律。如图2(a)所示，对于侧壁开口较小的模拟场景，热释放速率会在短时间内迅速升高，随后下降到近似为0。模拟场景A、B、C曲线基本重合，模拟场景D快速下降后呈现出一定程度振荡，最终降至近似为0。这说明，由于火源远离侧壁开口，通过较小侧壁开口流入的新鲜空气难以到达燃烧区域，导致后期火焰熄灭。如图2(b)所示，对于侧壁开口较大的模拟场景，热释放速率会在短时间内迅速升高，之后稳定在某一固定值附近振荡，趋于稳态燃烧状态。除场景H平均热释放速率(424.12)接近火源热释放速率设定值外，其余场景热释放速率均小于预设火源热释放速率，说明场景均处于通风控制阶段。

通过开口处烟气温度可以更直观地观察到房间内火焰变化趋势。图3和图4选取的是几种典型模拟场景的温度切片。可以看出，侧壁开口处烟气流动呈现双向流动和单向流动两种形式。如图3所示，场景A在火焰未熄灭时，火焰主要集中在开口处，气体流动形式以向外单向流动和向内单向流动为主，未出现双向流动现象，火焰熄灭后，冷热气体的交换主要集中在房间外，可认为外界冷空气无法进入房间。图4所示为侧壁开口稍大的模拟场景C、D、E，随着通风因子的增大，开口处气体流动形式从单向流动转变为双向流动，其混合区域也逐渐变大，并且出现游离火和溢流火现象。

(a)较小侧壁开口

2.2 侧壁开口的影响

如图5所示，对于无顶部开口场景，火灾热释放速率随侧壁开口通风因子(WH3/2)的增大而增加，二者近似成线性关系，这与前人研究结果一致。然而，随着顶部开口出现，火灾发展的基础水平(即侧壁开口较小场景的平均热释放速率)显著提升。与无顶部开口场景相比，在顶部开口尺寸为0.1 m×

图3 场景A的温度切片

图4 侧壁开口尺寸较大场景的温度切片

0.1 m、0.15 m×0.15 m，侧壁开口尺寸为0.2 m×0.2 m两个场景中，HRR提升了近2倍，说明顶部开口的出现促进了新鲜空间的流入，增强了火势。在所有顶部开口场景中，HRR与WH3/2依然具有一定线性关系。但随着顶部开口尺寸的增大，通风因子对火灾热释放速率的影响程度明显降低，特别是顶部开口尺寸0.3 m以上的场景，通风因子对HRR几乎无影响，而仅与顶部开口尺寸相关。这说明，利用侧壁开口通风因子预测具有顶部开口场景的热释放速率依然可行，但需要考虑顶部开口尺寸对HRR～WH3/2关系式初值和斜率的影响。

图5 侧壁开口条件对HRR的影响规律

2.3 顶部开口的影响

如图6所示，顶部开口尺寸对侧壁开口尺寸较小的场景影响较为明显。随着顶部开口尺寸的增加，HRR逐渐增加，最终达到火源HRR预设值，即可能达到最大热释放速率。对于通风受限火灾，HRR的增加表明进入燃烧区域的氧气在增加，顶部开口尺寸的变大使更多空气进入燃烧区域，促进火灾的发展。此外，顶部开口尺寸与HRR之间并非良好线性关系，存在一个临界开口尺寸使得HRR大幅提升。这说明，对于特定场景，当顶部开口尺寸增加到某一特定数值时，起火房间开口烟气流动模式将发生改变。

图6 顶部开口条件对HRR的影响规律

3 耦合开口通风因子的拟合分析

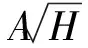
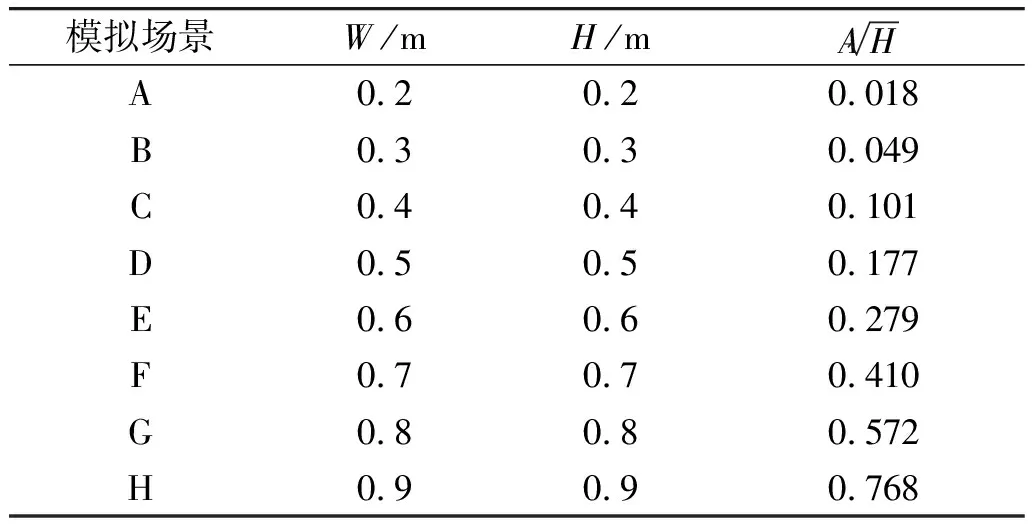
表3 侧壁开口尺寸及对应通风因子

由此可得，无顶部开口房间HRR(y)与侧壁开口通风因子(x)的拟合关系式为：

y=609.36x+19.1

(1)

当存在0.2 m×0.2 m顶部开口时，房间HRR和侧壁开口通风因子的拟合关系式为：

y=177.49x+275.72

(2)

最终得到，0.2 m×0.2 m顶部开口场景下折算通风因子与侧壁开口通风因子的关系，如表4所示。

表4 折算通风因子与关系

y=0.3192x+0.4106

(3)

通过校正，得出在有顶部开口情况下，通风因子的估算式为：

(4)

式中，As为顶部开口面积。

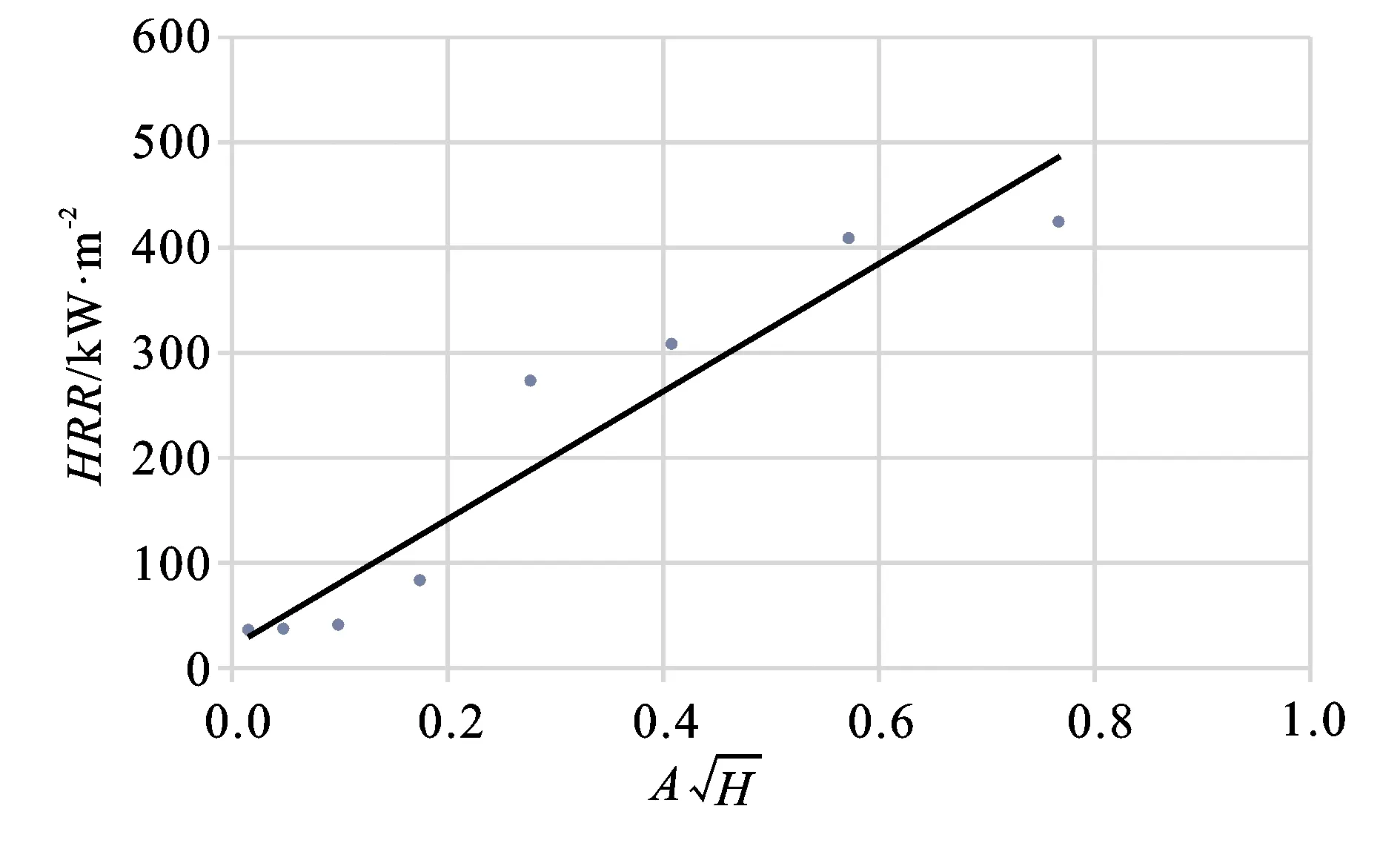
(a)无顶部开口场景

(b)顶部开口较小(0.2×0.2)场景

为验证公式的计算精度，对不同顶部开口尺寸下折算通风因子(见表5)与式(4)所得到的估算值(见表6)进行对比分析。可见，在顶部开口为0.1 m×0.1 m和0.15 m×0.15 m时，用式(4)计算出来的估算值与折算通风因子相差很多。分析原因，主要是模拟场景中火源远离侧壁开口，当侧壁开口尺寸较小时，开口处气体流动并未呈现出理论上下入/上出的流动模式，外界空气难以到达燃烧区域，导致火焰熄灭，这与理论上HRR与WH3/2存在线性关系相背。因此，估算通风因子明显高于折算通风因子，在工程应用上会使计算结果趋于安全。随着侧壁开口尺寸的增加，通风因子的估算值与折算值逐渐趋于一致。而在顶部开口为0.25 m×0.25 m和0.3 m×0.3 m时，通风因子的估算值与折算值较为相近。可以看出，随着顶部开口尺寸的增加，较大顶部开口在一定程度上弥补较小侧壁开口带来的计算误差，通风因子预测效果得以改善。此时，通风因子计算误差可能更多来自于复杂耦合开口烟气流动模式，以及顶部开口烟气流动对火源燃烧状态的影响。式(4)适于燃烧虽处于通风控制条件下，但火焰并未熄灭房间的通风因子估算。

表5 不同顶部开口下折算通风因子

表6 不同顶部开口下式(4)估算的通风因子

4 结论

采用数值模拟方法，对顶部和侧壁开口对起火房间热释放速率影响进行研究。结果表明：顶部开口和侧壁开口均会对起火房间的HRR产生影响，且为正相关。顶部开口会对起火房间通风模式产生影响，进而使HRR与WH3/2的线性关系发生改变。通过模拟分析耦合开口对火灾热释放速率的影响规律，建立有顶部开口情况与无顶部开口情况的通风因子换算关系式，得到适于计算同时具有顶部和侧壁开口起火房间通风因子的估算式。本文估算通风因子在一定程度上可以体现顶部开口尺寸对起火房间热释放速率的影响规律，且计算结果整体趋于安全，因此具有一定工程应用价值。