考虑微细超声加工系统动力属性的切割自校正控制
2022-06-27缪兴华高长水张熠飞夏华凤
缪兴华,高长水,张熠飞,夏华凤,3
(1.泰州学院 船舶与机电工程学院,泰州 225300;2.南京航空航天大学 江苏省精密与微细制造技术重点实验室,南京 210016;3.泰州学院 泰州市电能变换与控制工程技术研究中心,泰州 225300)
0 引言
随着我国工业制造技术的不断进步,高端制造业领域对微细零件、微细产品的生产工艺要求越来越高。超声切割技术的问世,使微细机械产品加工技术被广泛应用于电子、机械、通讯等高端制造领域[1]。
微细超声加工系统作为超声切割的重要载体,是微细切割中最常见的切割工具,其相关性能一度成为设计者们讨论的重要话题之一。对于微细超声加工系统来说,很多因素会影响切割刀的切割精度,从而降低生产效率。因此,需对系统割刀实施必要的精度控制,以此来缩减生产成本,提高生产质量。针对割刀切割精度控制方法中的精度失效问题,相关学者提出更加高效的精度控制方法,相关研究成为机械制造企业亟待解决的热门问题之一。
例如:文献[2]中针对切割的绝对尺寸展开控制,其分析了割刀的修整量、伺服进给速度、零件厚度对切割尺寸的影响,根据影响规律优化切割尺寸,并在修整量不变的情况下,对伺服进给速度的补偿量进行调整。文献[3]中将EtherCAT网络模型与计算机视觉技术相结合,对切割设备的位置和速度实施控制,降低了接线复杂度和调整不灵活的问题,并电控模块实现对待切割目标位置的调整。
然而在实际应用中发现,几乎当前所有的方法未对系统切割机器开展详细的动力学分析,且针对切割机加速度向量的分析也不够明确,导致其存在切割速度和精度低的不足。主要是因为相关动力学属性会使得控制条件复杂化,为解决上述精度控制过程中存在的问题,本研究提出了基于自校正模糊控制的微细超声加工系统切割精度控制方法。
1 微细超声加工系统切割过程的动力学分析
在研究微细超声加工系统切割精度控制过程前,本文需要对微细超声加工系统开展动力学分析,获取微细超声加工系统的加速度向量,从而依据向量分析结果,建立微细超声加工系统切割误差模型。
1.1 超声切割振动动力学属性分析
微细超声加工系统的割刀分为前后端块i1、压电陶瓷i2、变幅杆i3、电极片i4以及夹持件i5几部分。不同结构的位移向量用wli表述,即表示割刀i部分在l时刻的横坐标位置。获取割刀各个位置的振动动力学属性微分方程,过程如式(1)所示:
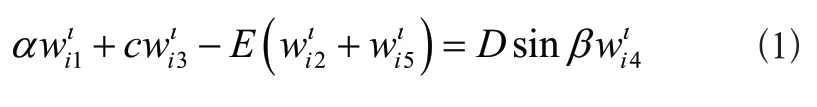
式(1)中,α表示割刀材质密度,E表示割刀材质弹性模量,c表示等效阻尼系数[4],D表示压电常数矩阵,β矩阵权重。
基于系统初始条件以及建立的振动微分方程,获取系统的割刀截面位移应力边界动力学属性约束条件,如式(2)所示:
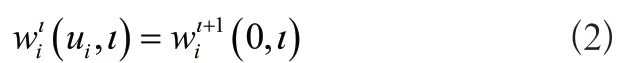
1.2 系统割刀加速度动力学属性分析
假设微细超声加工系统的割刀瞬时角速度为α,加速度为ω,依据系统结构分析结果获取系统结构坐标矢量投影,过程如式(3)所示:

式(3)中,r1表示系统结构横向坐标向量矢量,r2表示结构偏置距离坐标矢量,ra表示割刀曲柄角速度,rω表示连杆加速度,φ3、φ4表示夹角矢量,cos表示余弦夹角,sin表示正弦夹角。
由于割刀的套筒滑动杆的滑动距离较小[5],若割刀连杆与待切割目标夹角一致,可依据获取的运动学方程,获取割刀运动夹角,过程如式(4)所示:

式(4)中,割刀连杆与待切割目标夹角标记φ,安装角为,近似向量标记λ。
最后,依据上述计算结果,获取割刀连杆曲柄结构参数以及相关关系,并将其映射至η轴上,取得割刀得到加速度动力学属性向量,过程如式(5)所示:
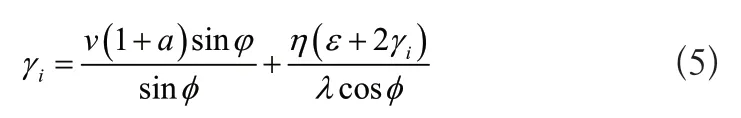
式(5)中,sin2φ表示割刀与目标的正弦夹角,cosφ表示割刀与目标的余弦夹角,ri表示获取的割刀加速度矢量,v表示割刀移动速度,ε表示映射因子。
2 考虑动力学因素的切割精度控制方法设计
基于割刀加速度矢量,通过相关计算分析获取微细超声加工系统切割的理想运动变换,建立系统的切割误差运动误差模型,再使用模糊自校正控制算法修正系统切割误差,提升系统切割精度,完成系统切割精度控制。
2.1 获取切割过程的理想运动变换模型
在上文分析的微细超声加工系统中,目标与割刀之间存在运动属性变换,基于上述计算出的割刀移动加速度向量,获取系统的理想运动变换。
假设微细超声加工系统割刀有若干部分,在坐标系Oi与Oj之间沿(X,Y,Z)方向移动。依据相关变换矩阵,获取系统各个方向的齐次矩阵Q(x)、Q(y)、Q(z),割刀平移方向标记x、y、z。将上述获取的各项齐次矩阵整合,取得最终的割刀理想变换模型,过程如式(6)所示:

式(6)中,Qw表示获取的最终理想平移变换矩阵。
由于割刀移动时,不仅存在平面移动,还存在旋转移动。因此,设定割刀旋转坐标为Oj(xj,yj,zj),轴转动系数标记θ、ϑ、ρ。在割刀旋转移动过程中,各个旋转方向的齐次矩阵分别为Qθ、Qϑ、Qρ形式。在经过参数整合后,得到理想的旋转变换模型如式(7)所示:

式(7)中,Q表示最终的割刀旋转最佳理想旋转模型。
2.2 建立切割空间误差数学模型
依据获取的割刀变换关系,获取割刀刀头的理想末端空间位置误差以及实际空间位置误差,设定理想刀头位置为d0,实际位置为d,则误差向量如式(8)所示:
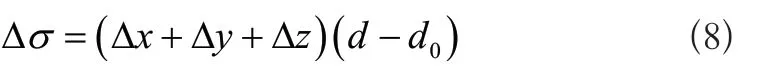
式(8)中,空间位置误差系数在X方向的系数值标记Δx,空间位置误差系数在Y方向的系数值标记Δy,空间位置误差系数在Z方向的系数值标记Δz,空间位置误差系数标记Δσ。
在此基础上,设定割刀刀头的坐标系位置为p=(0,0,c),齐次坐标位置用p`=(0,0,c,1),以此建立微细超声加工系统的切割误差模型,过程如式(9)所示:

式(9)中,R表示建立的切割误差模型,T0表示末端理想位置变换矩阵,[Os]p`表示实际位置变换矩阵。
根据上述建立的系统切割误差模型,计算系统割刀的末端切割误差,过程如式(10)所示:

式(10)中,e表示刀头末端切割误差,Ps表示刀头实际位置,Pl表示刀头理想位置,f表示逼近函数。
2.3 基于模糊自校正规则实现切割精度控制
以前两个章节的计算结果为基础,设定微细超声加工系统的待控制对象为d(u),获取过程以及选定的控制算法如式(11)所示:
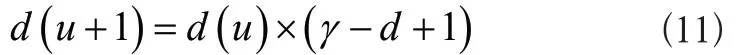
式(11)中,r表示待切割对象得到输入数据值,d表示输出数据,γ表示系统控制输入值。
依据上述确定的控制算法获取微细超声加工系统的模糊自校正约束规则,结果如式(12)所示:

式(12)中,δ表示模糊自校正规则,Ei表示输入动力学向量,E`i表示中心向量,r表示输入区域半径,y表示校正规则的模糊输出,c表示自校正规则数量,κ表示模糊校正系数,c表示常数系数。
为将精度控制问题简化,使用非零函数以及获取的校正规则,完成系统割刀的误差校正,实现微细超声加工系统的切割精度控制。具体的微细超声加工系统的切割精度控制流程如下:
步骤1:基于系统的动力学分析结果,获取系统的加速度向量。
步骤2:依据系统的理想运动变换,建立系统切割空间误差数学模型,完成切割误差的获取。
步骤3:最后通过迷糊自校正规则校正割刀位置误差,提高切割精度,完成系统的切割精度控制。
3 实验与结果分析
为了验证上述设计的微细超声加工系统切割精度控制方法的整体有效性,设计如下测试过程。实验场景如图1所示。

图1 实验场景图
实验中应用的是全自动双面微细超声切割设备,设备参数如下:切割宽度:4mm~1580mm;可切直径:250mm~500mm;安装割刀:Φ250~500mm;额定电压:220V/380V;机身尺寸:2800×1500×1500mm。控制算法以单片机拷入形式实现。
为避免实验结果的单一性,分别采用本文的微细超声加工系统切割精度控制方法(本文方法)、文献[2]方法、文献[3]方法开展对比测试。
在实验验证中,微细超声加工系统控制速度的高低、能耗的大小以及控制精准度的优劣,都是检测控制方法控制性能的重要检测指标。为此,采用本文方法、文献[3]方法以及文献[4]方法实施精度控制时,依据上述指标测试控制方法的控制性能。
实验1:检测应用不同方法控制后的切割速度
在控制系统切割精度时,切割速度的高低会影响切割效果。设定不同的待切割目标材料厚度,采用本文方法、文献[2]方法实施精度控制时,对两种方法的切割速度展开测试。切割速度越快,证明切割效率越高。测试结果如图2所示。
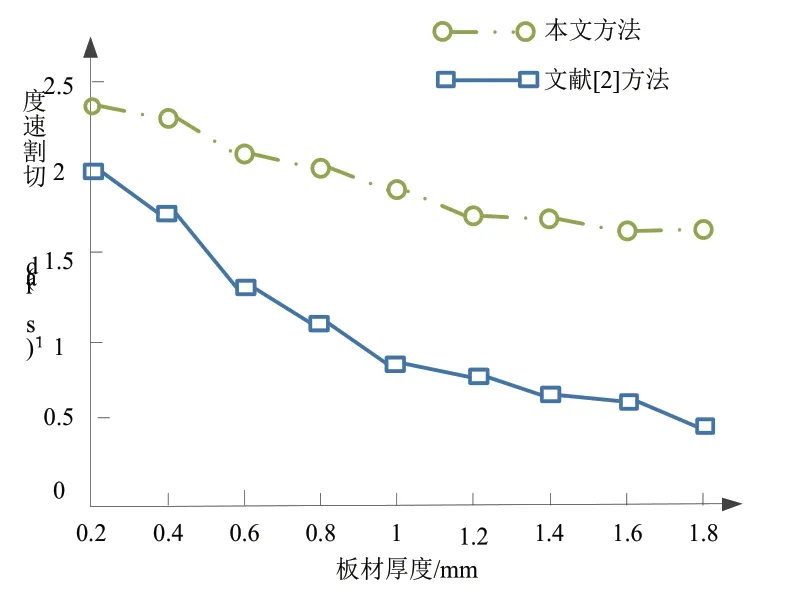
图2 不同方法的切割速度测试结果
分析图2所示的测试数据可知,待切割板材厚度不同能够影响系统的切割速度,待切割板材厚度越大,测试出的切割速度越低。应用本文方法控制后,微细超声加工系统的切割速度高于应用文献[2]方法控制后的切割速度测试结果。这主要是因为本文方法实施切割精度控制前,对切割系统开展了详细的动力学分析,所以本文方法在完成切割任务时的切割速度高。
实验2:检测应用不同方法控制后的切割能耗
在开展系统精度控制时,系统工具的能耗同样能够影响系统的控制精度。选取控制目标尺寸、振幅为控制能耗测试指标,以此测试不同控制方法的控制能耗。测试结果如图3、图4所示。

图4 不同工件尺寸下控制方法的控制能耗测试结果
依据图3所示结果可知,待控制目标的工件振幅越高,所测试出的控制能耗就越大。本文方法在工件振幅为40·10-5/min前,测试出的能耗未发生变化,直至工件振幅大于40·10-5/min后,测试结果逐渐增大。从整体来看,文献[2]方法与文献[3]方法的切割能耗测试结果远高于本文方法。
依据图4所示结果可知,随着控制工件尺寸的不断增大,所耗费的功耗随之增多。本文方法虽然会随着工件尺寸的增加而提高控制能耗,但是测试结果依旧低于其他两种方法的控制能耗测试结果。
由此可知,本文方法在实施系统精度控制时,能够有效降低系统的控制能耗,证明该方法存在有效性。
实验3:检测应用不同方法控制后的控制精度测试
设置理想的控制误差区域为[-0.5,0.5]mm,分别采用本文方法、文献[2]方法以及文献[3]方法实施精度控制后,测试三种控制方法的控制精度,结果如表1所示。
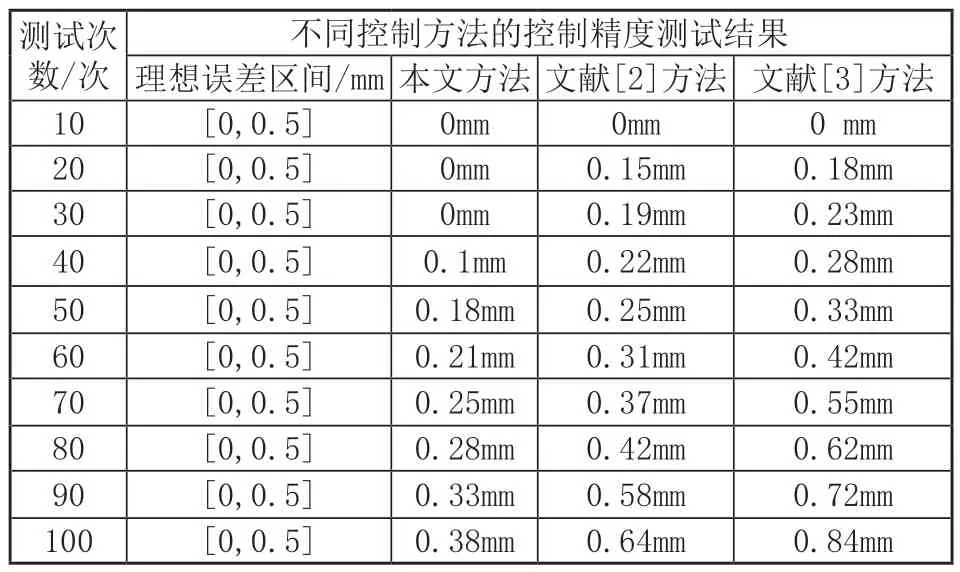
表1 不同控制方法的控制精度测试结果
分析表1所示的测试数据可知,随着测试次数的增加,三种控制方法误差测试结果均呈现不同程度的上升趋势。本文方法测试结果低于文献[2]方法以及文献[3]方法的控制误差测试结果,可由此证明本文方法的控制精度更高。
综上所述,本文方法在开展切割精度控制时,切割速度快、控制能耗低、控制精度高,证明本文方法控制效果更好。
4 结语
随着我国工业的高速发展,微细零件生产产量逐年增加。微细超声加工系统的出现更是提升了零件的切割效率。因此,针对传统系统切割精度控制方法中存在的问题,本研究提出了一种考虑动力学属性和自校正模糊控制的,微细超声加工系统切割精度控制方法。
该方法依据获取的系统割刀加速度向量建立割刀位置误差检测模型;并使用模糊自校正控制方法对检测出的误差实施校正修复;最后基于校正结果完成微细超声加工系统的切割精度控制。该方法由于在建立误差模型时存在些许缺陷,今后会针对该项问题,继续对该控制方法实施优化处理,直至方法完善。
