Sage-Husa自适应滤波在运动障碍物轨迹预测中的应用

孙立新，侯 阳

（河北工业大学 机械工程学院，天津 300130）

0 引言

随着机器人技术不断发展，人们对机器人与环境的交互能力的要求也不断提高。机器人在复杂的工作环境下，需要对接收到的障碍物的运动信息作出分析，从而安全准确地避开障碍物完成工作，因此对运动障碍物的轨迹预测是机器人智能化的关键技术。运动障碍物轨迹预测包含状态获取、多步迭代、矫正优化等机制[1]，卡尔曼滤波（KF）作为一种线性最优的滤波方法[2]，在目标预测方面具有计算量小、便于实时处理、预测效果较好等优点，近年来被广泛应用于各个领域[3～5]。

然而该算法没有考虑到实际情况下系统噪声的实时变化，因此随着研究的深入，出现了许多自适应卡尔曼滤波算法（AKF），如新息自适应估计卡尔曼滤波算法、模糊自适应滤波法算法、贝叶斯估计法、极大似然法等[6]。旨在滤波过程中对噪声的变化作出预估与更新，从而对预测值作出更加精确的修正，提高滤波精度。本文采用Sage-Husa自适应滤波方法实现对运动障碍物的轨迹预测，该方法计算简便、步骤清晰、更加满足实际需要，其实验结果具有普遍意义。

1 状态空间模型建立

建立被测物体离散时刻下线性随机系统状态空间模型，它由状态方程和观测方程组成。状态方程描述了物体在两个时刻间的状态变化，观测方程描述了实际观测量与状态变量之间的关系：

式中：k—离散时间；Xk—被测物体在时刻的状态向量；A—状态转移矩阵；B—控制增益矩阵；Uk被测物体在时刻的控制输入；Zk—被测物体在时刻的观测值；H—观测矩阵；Wk、Vk分别表示系统的状态噪声和观测噪声，它们都是互相独立的高斯白噪声，设噪声均值分别为qk、rk，方差为Qk、Rk，则可表示为：

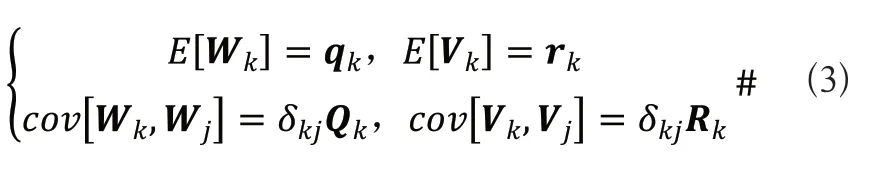
2 Sage-Husa自适应滤波

如果噪声均值为qk、rk为0，且噪声方差Qk、Rk均为已知，则卡尔曼滤波公式如下所示，它是一种基于递推线性最小方差估计准则的最佳估计，其过程分为预测过程和修正过程，预测过程是根据上一时刻的被测物体的状态与协方差进行推测，以此预测出这一时刻的状态，得到被测物体状态的先验估计；修正过程以观测数据作为反馈，对预测值进行修正，获得被测物体的后验估计。

预测过程：

修正过程：

然而在实际情况下，噪声均值qk、rk并不一定为0，且qk、rk、Qk、Rk部分或者全部未知并随时间不断变化，这对于卡尔曼滤波的预测结果产生了干扰。Sage-Husa自适应滤波在卡尔曼滤波预测-修正过程的基础上，增加了实时运用观测更新的数据对状态噪声和观测噪声进行动态的统计估计[7]，更新噪声均值与方差qk、rk、Qk、Rk，从而减少噪声的变化对预测结果带来的影响。其基本算法如下所示：

使用Sage-Husa自适应滤波预测物体运动轨迹的基本步骤如下：首先对被测物体建立状态空间模型，根据运动学方程确定状态转移矩阵A和观测矩阵H，根据控制输入变量确定控制增益矩阵B；其次经过自适应滤波的预测过程，根据上一时刻的状态向量Xk-1和协方差Pk-1预测这一时刻的状态向量Xk|k-1和协方差Pk|k-1；再加入被测物体的观测数据Zk，将预测出的Xk|k-1，Pk|k-1修正为Xk，Pk；最后将状态噪声和观测噪声的均值与方差qk-1、rk-1、Qk-1、Rk-1，更新为qk，rk，Qk，Rk，为下一次迭代做准备。完成上述一个周期的迭代，可得到被测物体在时刻位置的单步预测。只要将所得到的Xk，Pk，qk，rk，Qk，Rk，作为下一时刻的初始值，进行多次迭代，最终可以得到被测物体运动的预测轨迹。

3 运动障碍物轨迹预测

3.1 运动障碍物状态模型建立

模拟障碍物在XOY平面内运动，运动中的位移，速度，加速度记为p，v，a，它们随时间的变化不断变化。在任意一个时刻内可将障碍物的运动分解为沿X方向和沿Y方向的直线运动，其位移记为px，py；速度记为vx，vy；加速度记为ax，ay，其运动学分解如图1所示。

图1 障碍物运动学分解

建立障碍物的运动状态变化：状态向量Xt-1从t-1时刻到t时刻间的时段Δt内沿X，Y方向分别以加速度ax(t-1)、ay(t-1)转变到下一个状态向量Xt，则运动障碍物在Δt内运动的状态方程可描述为：

因最终要实现轨迹预测，应选取X，Y方向的位移作为观测值，所以观测矩阵H为：

状态噪声Wt与观测噪声Vt为实际预测过程中引入的噪声，其均值qt、rt和方差Qt、Rt根据实际情况确定。

3.2 运动障碍物轨迹预测仿真

设运动障碍物起始位置为（0，0），初始速度vx=3m/s，vy=6m/s，传感器采样时间间隔为Δt=0.5s，采样次数为120次，运动总时长T=0.5×120=60s。则初始状态向量为：

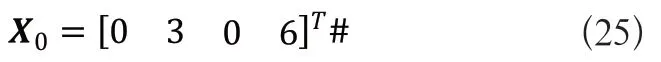
该模型的控制输入为ax，ay。为检验在障碍物的运动状态不断变化过程中Sage-Husa自适应滤波的预测效果，取ax，ay，为振幅、频率互不相同的弦函数输入，其图像如图2、图3所示，横坐标代表采样次数：

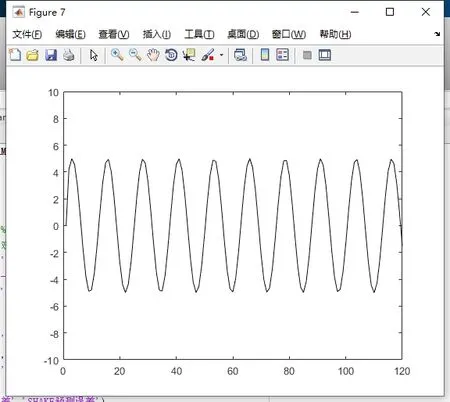
图2 X方向加速度输入

图3 Y方向加速度输入

仿真给出了障碍物运动过程的理想轨迹，传感器传回的观测轨迹，卡尔曼滤波预测轨迹和Sage-Husa自适应滤波的预测轨迹。综合以上四条轨迹的比较与分析，即可得到对Sage-Husa自适应滤波预测效果的评价，取遗忘因子b=0.99。

图4中显示了观测轨迹和两种算法预测轨迹都能以理想轨迹为中心进行波动。从图上可以看出，不加入滤波算法的情况下，仅靠传感器传回的数据拟合运动轨迹受噪声影响较大，轨迹呈不规则锯齿状，预测精度很低。而卡尔曼滤波算法和Sage-Husa自适应滤波算法对障碍物运动状态的变化都具有很高的预测精度，其预测轨迹更加光滑、平整。证明了两种算法不仅在理论上能很好的对运动障碍物进行轨迹预测，而且具有实际的可行性。图5展示了运动轨迹曲线的局部放大图，对比卡尔曼滤波算法和Sage-Husa自适应滤波算法预测轨迹可知，Sage-Husa自适应滤波预测轨迹更加贴合理想轨迹，其预测效果更好。

图4 运动障碍物轨迹预测

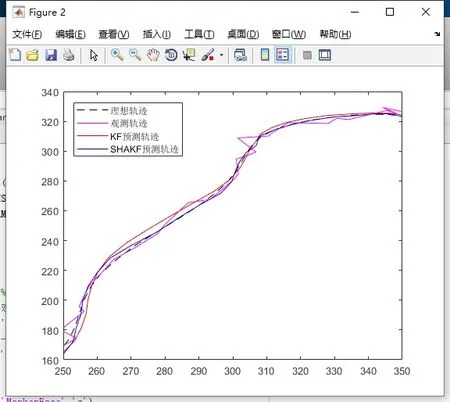
图5 局部放大图

3.3 误差分析

为定量分析Sage-Husa自适应滤波的预测精度，引入同一时刻下观测轨迹点、卡尔曼滤波预测轨迹点、Sage-Husa自适应滤波预测轨迹点到理想轨迹点的几何误差[9]，对误差进行比较，得到并分析误差分布的统计特性。该误差采用欧式距离计算公式求出：

其中(x，y)为t时刻理想轨迹点的坐标；(x′，y′)为t时刻观测轨迹点的坐标；(x"，y")为t时刻卡尔曼滤波预测轨迹点的坐标；(x'''，y''')为t时刻Sage-Husa自适应滤波预测轨迹点的坐标；RMS1表示观测误差；RMS2表示卡尔曼滤波预测误差；RMS3表示Sage-Husa自适应滤波预测误差，其结果如图6所示，横坐标代表采样次数：

图6 误差分析

三组误差的统计特性如表1所示：

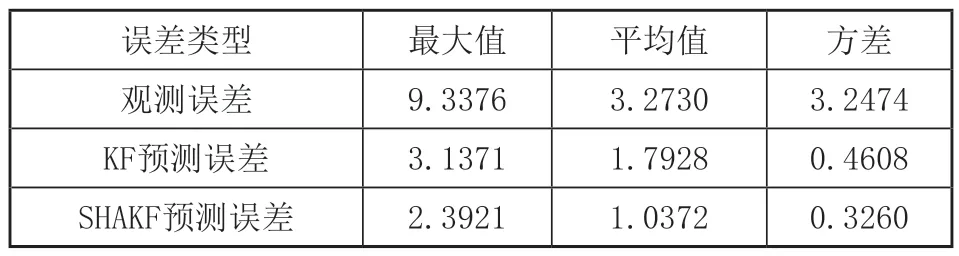
表1 误差统计特性

从表1可以得到，卡尔曼滤波预测误差与Sage-Husa自适应滤波预测误差最大值分别为3.1371、2.3921，相比观测误差最大值减少了66.40%、74.38%；误差均值分别为1.7928、1.0372，相比观测误差均值减少了45.22%、68.31%，说明Sage-Husa自适应滤波比卡尔曼滤波在降低噪声对预测过程带来的误差中有更显著的作用，其轨迹预测精度更高。而Sage-Husa自适应滤波预测误差方差为0.3260，小于卡尔曼滤波预测误差方差0.4608，说明Sage-Husa自适应滤波相比卡尔曼滤波预测过程更加稳定，不易产生突变，预测轨迹更加平滑。

4 结语

本文针对机器人在复杂工作环境下的避障和传感器的观测值存在噪声等问题，提出使用具有时变性能的噪声估计器的Sage-Husa自适应滤波对运动障碍物的运动轨迹进行预测。从理论分析、运动状态建模、仿真实验、误差分析等方面完整阐述了该方法的可行性。相比传统卡尔曼滤波，Sage-Husa自适应滤波具有噪声处理更好，预测精度更高，预测轨迹更平滑等特点。且对于障碍物运动状态的不断变化也具有很强的适应性，为机器人实现自主避障功能提供了可靠信息。但该方法仍有其局限性，例如该方法不适用于障碍物运动状态为非线性的系统等，这些问题有待进一步的研究论证。