基于卷积神经网络的地铁牵引电机轴承剩余寿命预测

赵朋飞，徐彦伟,2，颉潭成,2*，李 琛

（1.河南科技大学 机电工程学院，洛阳 471003；2.智能数控装备河南省工程实验室，洛阳 471003）

0 引言

随着服役时间的不断增加，机械设备性能逐渐衰退，剩余寿命逐步缩短，设备中任何一个关键部件失效，均易造成恶性事故，导致经济损失，甚至人员伤亡[1]。轴承作为机械设备零部件的一种，研究其寿命退化趋势并对轴承剩余使用寿命（Remaining useful life，RUL）做精准预测，能为机械设备的预测性维护提供指导[2]。

近年来，轴承的剩余寿命预测已成为国内外学者研究的热点[3]，张成龙、刘小勇、武千惠[4～6]等在轴承寿命预测方向获得了不错的成果，但他们将单一特征值输入到模型中进行训练，提取到的轴承寿命信息有限，没考虑采用多特征值进行信息融合，使用多特征值信息融合技术可以提高预测的精度。随着信息融合技术的发展，越来越多学者加入其中进行研究，杨彦宇、王付广、蒙志强[7～9]等使用信息融合技术在轴承剩余寿命预测方向的研究得到不错的成果，并在信息融合技术上提供有益的借鉴，但他们采用了单一类传感器，采集到的信息不能全面反映轴承寿命信息，会影响对轴承寿命的预测。

基于此，本文提出了一种基于多信息融合与卷积神经网络的轴承剩余寿命预测的方法。首先，使用振动传感器与声发射传感器在轴承疲劳试验台上采集轴承寿命信号；其次，使用小波包分解[10]对采集到的原始信号进行降噪并提取多特征值，在此基础上对多特征值进行归一化处理并分析轴承退化趋势；最后，将处理好的多特征值进行融合，并输入到卷积神经网络中进行训练来预测轴承的剩余使用寿命。

1 信号预处理与退化指标选取

1.1 信号采集和预处理

本文确定研究轴承的型号为NU216，它作为地铁牵引电机轴承，对地铁安全运行起着至关重要的作用，所以预测该轴承的剩余使用寿命显得尤其重要。为了减少试验周期，模拟轴承实际运行中产生的早期缺陷，采用大族YLP-MDF-152型三维激光仪在滚动体上进行缺陷预制，缺陷预制过程当中使用30%的激光能量，预制点蚀直径为20μm，裂纹宽度为15μm的早期故障缺陷，在此基础上探究其剩余寿命，进行剩余寿命试验，所选用的试验台为T40～120，位于智能数控装备河南省工程实验室，该试验台由液压系统（提供加载、冷却和润滑）、温度测量系统、压力测量系统和数据采集系统等组成。在数据采集系统中传感器有声发射传感器（型号为R50S-TC，测量范围50KHZ-700KHZ，最高采样频率为10M/S）和振动传感器（型号为LC0151T，量程为33g、灵敏度为150mv/g）。该试验台如图1所示。

图1 轴承疲劳寿命试验台

试验按照GB/T24607-2009国家试验标准进行，在径向当量动载荷为40kN，转速为2400r/min的工况下对轴承进行120小时的疲劳寿命强化试验。每10min采集一次轴承状态数据，试验完成后共采集到720组轴承性能衰退试验数据。在采集到的原始信号中包含着大量的噪音，为了对原始信号进行滤波降噪处理，本文对原始信号进行小波包分解。小波包分解是一种更为细致的时频域分析方法，对原始信号的高频和低频同时进行多层分解，保证了信号在不同频段都有较高的分辨率，极大提高了信号分析能力[11]。

使用小波包分解对信号进行n次分解，每一次分解都会对上一次分解得到的信号进行高频与低频信号的分解，分解之后的信号在不失真的同时也保留轴承寿命信息。假设从单个传感器提取得到的特征向量为Zi(i=1，2，…，k)，故多传感器综合得到的特征向量为W×Zi，其中Zi的展开式如式(1)所示：

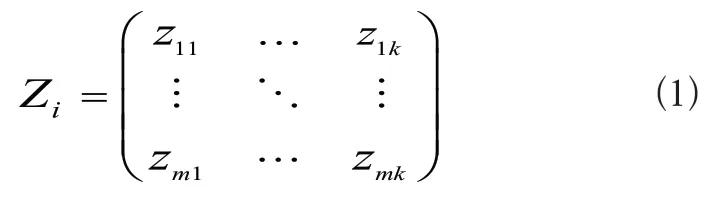
其中，W为传感器个数，k表示提取的特征值个数，m表示样本的个数。本文选用db4小波基函数，并对原始信号进行八次小波包分解，对得到的各个频率段进行多特征值的提取。

1.2 轴承剩余寿命退化指标选取

提取性能衰退敏感的特征对准确预测轴承剩余寿命尤为重要[12]，对原始信号进行小波包分解之后，需要对得到的高低频信号进行特征值提取。本文采用傅里叶变换对原始信号进行频域分析，用小波包分解对原始信号进行处理，以此来提取时域信号的特征值。时域特征分为有量纲和无量纲，其中有量纲的时域特征有标准差（SD）、均方根值（Root mean square，RMS）等，无量纲的时域特征有峭度（Kr）、裕度（C）等。它们的公式如下：

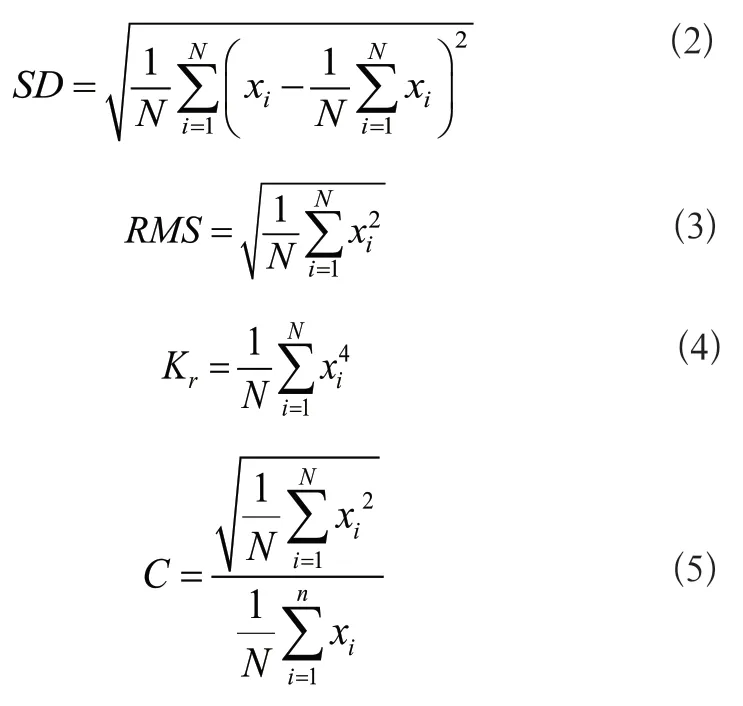
根据上面的公式计算得到标准差、均方根值、峭度和裕度，部分计算结果如表1、表2所示。

表1 振动传感器采集轴承寿命的特征值

表2 声发射传感器采集轴承寿命的特征值

从上述表1、表2中可以看出同一传感器在不同特征值之间由于数值的量级不同不能直接进行融合；同时同一特征值在不同传感器之间数值单位也不一样，也不能直接进行融合，因此需要我们进行归一化处理把它们映射到同一区间，在同一区间内进行融合。

2 信息融合与模型搭建

2.1 特征值的融合

在工程实践中，滚动轴承往往通过振动信号来反映其寿命衰退过程，从而进行寿命状态识别和寿命评估[13]，但为了应对单一类传感器带来的不足，本次试验采用振动和声发射传感器对轴承寿命信息进行采集，对采集到的信号进行预处理、特征值提取之后不能直接进行融合，因为不同传感器采集到的数据的物理意义不一样，需要进行归一化处理。

归一化是指从一个区间映射到另外一个区间，假设我们提取的原特征值区间为(X1，X2)，归一化之后的区间为(Y1，Y2)，设归一化之前数据为G，归一化之后的数据为H，那么G与H之间存在的映射关系为：

这个映射关系为线性关系，经推导可得：

信息融合技术是以归一化为前提，具有多传感器测量结果互补的特点，信息融合可对其参数重要程度进行评估和决策[14]，信息融合按照融合的方式分为数据层融合、特征层融合和决策层融合三种，数据层融合属于最原始的融合[15]，丢失的信息最少，但是由于声发射传感器和振动传感器存在探测技术的差别，因此不采用数据层融合，特征层融合属于把提取到的特征值进行融合，虽然丢失了部分信息但是可以通过归一化处理，来消除传感器之间的差别进行融合，而决策层融合会丢失大量的信息，所以本次实验采用特征层融合。

将采集得到轴承寿命信息进行特征值提取，从表2可知提取得到的特征值不能直接进行融合，需要进行归一化处理，然后进行特征值融合。将融合好的720组数据，抽取其中120组作为测试组，剩余的600组作为训练组，并把测试组与训练组划分5个阶段，将划分好的测试组与训练组进行打标处理，并输入到搭建好的神经网络中进行训练。

2.2 基于多信息融合与CNN的轴承剩余寿命预测模型

卷积神经网络是由多层网络构成的前馈神经网络，借鉴于LeNet-5结构，对卷积神经网络进行改进，初步确定卷积核大小为3×3，随后选择激活函数，卷积神经网络的激活函数有Sigmoid、tanh和relu等，激活函数初步选择relu，在卷积层进行特征信息提取然后传递给池化层之后，池化层进行特征选择和信息过滤，初步确定池化矩阵为2×2，需要全连接层对提取的特征进行非线性组合以得到输出，输出层选择Softmax分类函数进行分类。其卷积神经网络结构如图2所示。

在归一化之后，需要训练卷积神经网络，将归一化处理过的数据输入到神经网络，并对卷积神经网络模型中的卷积层与池化层的层数进行调整，最终确定为两个卷积层-池化层，全连接层为2层，其中卷积核大小为3×3，其滑动步长设置为1，池化矩阵为2×2，池化层的池化矩阵的移动步长为2，第一层激活函数为relu，第二层激活函数为tanh，使模型达到最佳状态训练次数（Epochs）为100。流程图如图3所示：

图3 模型搭建流程图

在上述工作完成之后，将各个传感器得到的归一化的特征值输入到调试好的神经网络中得到的识别率如表3所示。

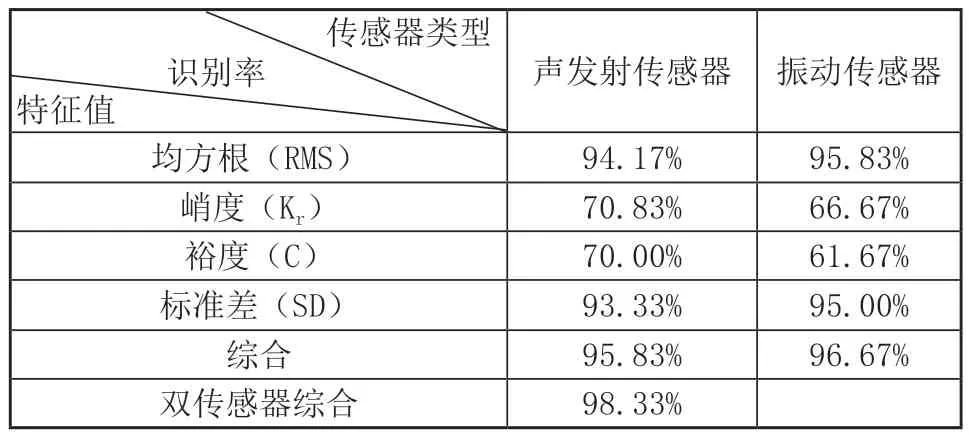
表3 各归一化的特征值识别率

从表3来看，不同特征值识别率不尽相同。其中均方根值的识别率最好，说明均方根提取到轴承寿命信息最多，标准差、峭度、裕度依次降低，说明它们提取到轴承寿命信息依次减少。通过表3可以看出将处理好的特征值进行融合，就单一传感器来说，不同特征值之间融合能提高预测剩余寿命的准确率，表明不同特征值提取到轴承寿命信息有共性也有差异。通过不同传感器之间的融合，可以看出预测轴承剩余寿命的准确率也得到了提高，说明不同传感器之间可以通过互补来提高轴承剩余寿命预测的准确率。

3 数据的分析

通过对归一化后的特征值进行分析，得到轴承寿命趋势如图4、图5所示：

图4 振动传感器采集的轴承寿命曲线图

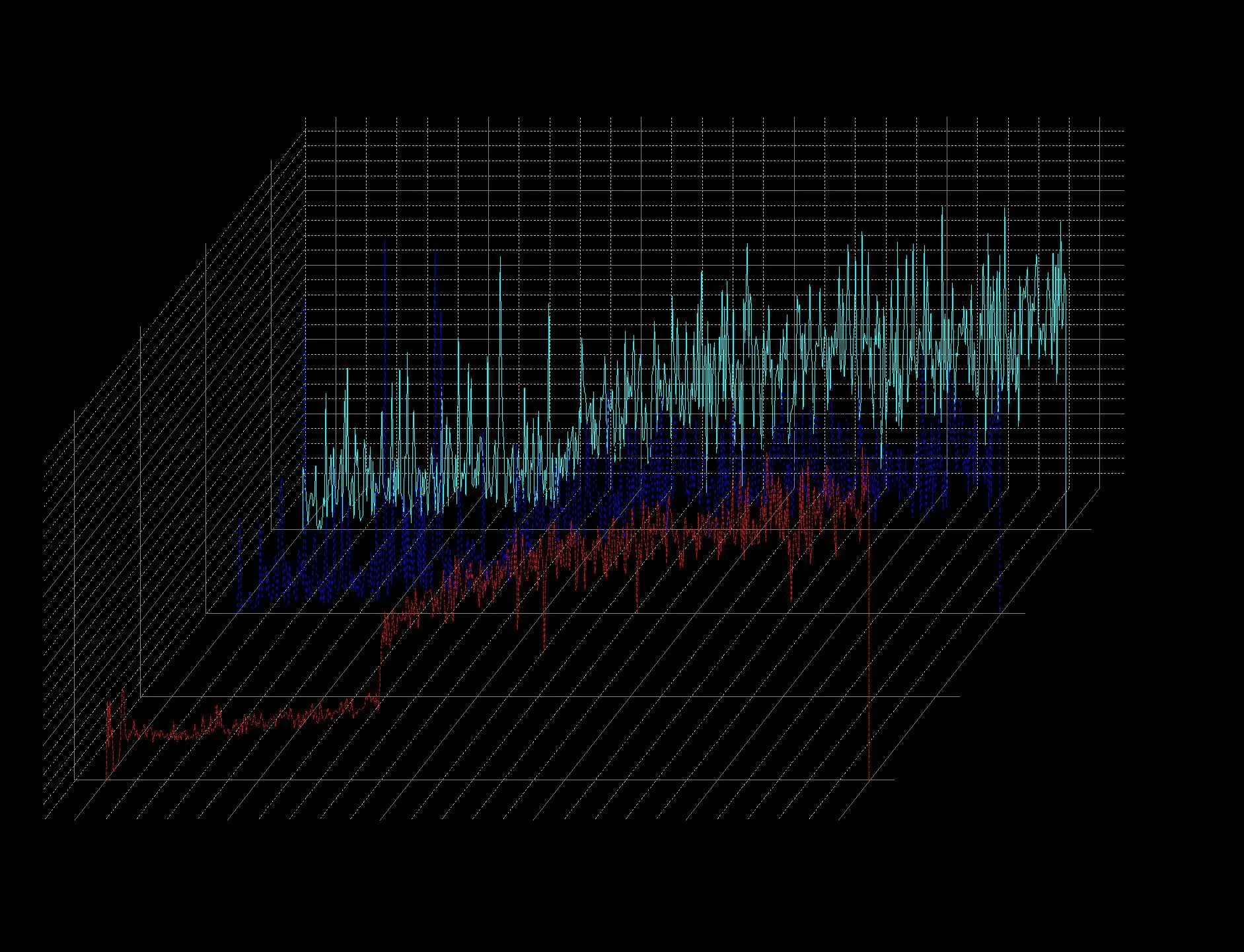
图5 声发射传感器采集的轴承寿命曲线图

从图4中可以看出除了峭度指标的趋势向下，其他指标的趋势都是向上，这表明峭度指标提取到轴承寿命信息最少，而均方根与标准差这两个指标提取到的轴承寿命信息比裕度多。图5为声发射传感器采集到的轴承寿命趋势图，从图5中可以验证上述的结论。

从图4、图5中可以直观看出，随着轴承运行时间的增加，轴承的寿命指标越来越大。通过分析可以得到无量纲的峭度、裕度作为轴承寿命指标不如有量纲的均方根与标准差。综合两种传感器来看，振动传感器在均方根与标准差方面比声发射传感器好，声发射传感器在裕度和峭度方面比振动传感器好。

从图4、图5中可以看到都是同一轴承寿命指标，上下波动量不同。为探究上下波动量对准确率的影响，以均方根为例，将从两种传感器得到的均方根输入到卷积神经网络中得到各个阶段的准确率的色阶图，如图6所示：

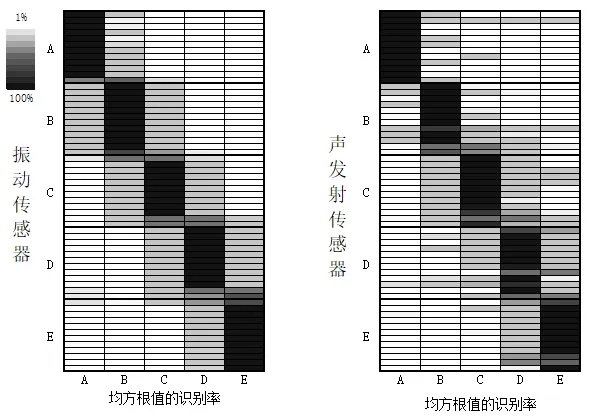
图6 均方根值识别率的色阶图

上述图中A、B、C、D、E代表轴承寿命的五个阶段，A代表第一阶段、B代表第二阶段、C代表第三阶段、D代表第四阶段、E代表第五阶段。本实验是在发现轴承出现早期缺陷之后进行的试验，第一阶段为轴承早期缺陷，第五阶段为轴承寿命采集最后的阶段。总共采集了720组数据，把采集到的数据分为测试集与训练集，其中测试样本为120组，训练样本为600组。在训练过程中对每一组的测试样本，神经网络都会输出这五个阶段的概率值，120组的测试样本输出120×5个概率值，将120组每两组求一个平均值作为新的概率值，将得到新的概率值制作成图6色阶图，在该色阶图中颜色越深代表着概率越高。

从图6中我们可以看到振动传感器在第一阶段、第二阶段表现得不如声发射传感器，但在其他阶段比声发射传感器好，这表明将这两种传感器得到信息进行融合有利于提高轴承剩余寿命预测的准确率。同时在图6中我们可以看出两个相邻阶段的准确率比阶段中间部分要低。

以均方根值为例，从图4、图5与图6中可以得到，在第一阶段声发射传感器采集到的寿命曲线的波动量比振动传感器的小，此时我们看到声发射传感器在第一阶段准确率高。对比其他阶段可以发现轴承的寿命曲线的波动量越小，轴承寿命所处阶段的准确率越高。整体来看振动传感器采集到的轴承寿命曲线波动量比声发射传感器的小，因此振动传感器在轴承寿命预测方面比声发射传感器更好。

4 结语

本文研究了深度学习与信息融合技术在地铁牵引电机轴承剩余寿命方面的预测，试验结果表明：

1）针对采集轴承寿命信号进行小波包分解并提取特征值进行归一化，发现振动传感器在有量纲方面表现的比声发射传感器好，而声发射传感器在无量纲方面表现要比振动传感器好。

2）经过对比可以得出，振动传感器在轴承寿命曲线上波动比声发射传感器小，同时采用两种类型传感器要比采用单一类型传感器识别率高。

3）通过使用特征层融合实现了不同类型传感器信息融合并且结合卷积神经网络能有效预测轴承剩余寿命。