地理空间信息扩散技术实证研究*——以四川省三台县洪水灾害为例

黄崇福，张馨文

(1.北京师范大学 环境演变与自然灾害教育部重点实验室，北京100875；2.北京师范大学 地理科学学部灾害风险科学研究院，北京100875)

在世界格局发生急剧变化的今天，人们只有超越以往的经验化模式，才能更好地认识世界，包括形形色色的地表现象。自然灾害，是一种综合自然和人文特征的地表现象，用以往案例形成的成灾经验，很难正确认识环境和社会均发生了显著变化的自然灾害。

以重大自然灾害灾情快速评估为例，以往的经验化模式，是用历史灾害资料建立经验公式，一旦发生自然灾害，根据致灾因子强度和灾区的自然和社会数据，用这些公式对灾情进行快速评估。例如，一旦发生破坏性地震，可根据震级对灾情进行粗估[1]。这类远隔千山万水的快速评估，我们称之为“隔空判灾”[2]，缺点是精度较低，大多只能保证不出数量级错误(相差在10倍之内) ，而且只能对县及县以上地理单元内的灾情进行评估[3]，很少细化到乡镇，更无法细化到村庄，评估结果支撑不了精准救灾。

现代信息技术的发展，为较高精度地快速评估灾情和救助需求，提供了一条新路径：由基层灾害信息员、卫星遥感和无人机等观测得到的局部数据，推测全灾区的情况。已观测地理单元是采点，空白单元是信息孤岛。外推的依据，是从观测得到的数据中总结出的因果关系。这类借助实时数字化技术进行的快速评估，我们称之为“采点外推”[4]，优点是自然和人文的变化已经在采点数据中体现，推测出的空白地理单元中的灾情精度较高，可细化到村庄，助力精准救灾。推测，是一种判断各种各样情况的行为，甚至于有纯主观性的层次分析法[5]，半主观的模糊综合评价[6]，常见的则是统计回归[7]。

当我们灾后第一时间采集灾区数据时，受信息员数量少、卫星扫描时段不凑巧、天气多云、投送无人机耗时长、灾区部分通讯中断等不利影响，2 h内获得灾情数据，只能覆盖灾区的部分地理单元，覆盖不了信息孤岛。只有推测出信息孤岛中的灾情，才能对整体灾情有较全面的认识，才能科学地制定出精准救灾方案。

在地理学中，有很多种数学插值法被用来研究推测问题。然而，除温度、降雨量等物理场外，多数地理特征值在空间上的分布，并不连续，数学插值的结果，误差较大。于是，统计回归方法(Statistical Regression Method)和人工神经网络(Artificial Neural Networks，ANN)等，被用来研究地表现象中的推测问题。但是，当观测数据提供的样本较小且样本点间有矛盾冲突时，这些方法的精度都不高。

理论和仿真实验证明，由于地理空间信息扩散技术，对被插值的参数，既没有连续性的要求，也没有与自变量间线性关系假设的约束，还具有优化处理小样本的功能，矛盾冲突也不影响总结学习因果关系的收敛性，所以能明显提高推测精度[8]。本文通过对四川省绵阳市三台县洪水灾害的实证研究，演示地理空间信息扩散技术在推测精度方面的优势。

1 地理学中的插值法

插值(Interpolation)是一个数学概念：给定函数f(x)在n个互异点的值f(xi)，i=1,…,n,寻求函数φ(x)逼近f(x)，若要求φ(xi)逼近f(xi)，则称之为插值问题。φ(x)称为f(x)的插值函数，xi称为插值节点。用φ(x)推测插值节点间任一点的函数值，称为插值；φ(xi)对f(xi)的逼近，称为似合。

直观地讲，用离散数据估算出其背后的函数在其它点处的近似值，就是数学插值。基本的数学假设是离散数据产生于一个连续函数。插值的目的是填充离散数据，形成较完整的函数图像。

物理空间中的插值，是人们试图对尚未实际测量场的连续场的值进行合理估计。空间插值用于地理学，则是指人们试图对尚未观测的地理单元的某个地理特征值进行合理估计。与数学插值较大的区别是，数学上的插值节点没有几何大小，而地理学中的插值节点是有几何大小的地理单元，从极细的栅格点，到行政单元，都是有几何大小的地理单元。

正如人们在地理制图中，利用有限个点处的取值，使用插值算法，计算丢失的信息，填充图像一样，人们在地表现象研究中，也利用有限个地理单元上的取值，使用插值算法，推测没有取值单元上的情况。所不同的是，制图插值涉及的单元通常很小且形状规则，能近似满足插值函数对连续性的要求；而地表现象中的单元，通常较大且不规则，其上的地理特征数据分布，并不连续。

人们在GIS中使用的插值技术，分确定性方法和地统计方法两种，例如，全局多项式、局部多项式、样条插值、反距离加权等，是确定性方法；而克里金法(Kriging)、地理加权回归(Geographically Weighted Regression，GWR)是地统计方法(Geostatistical Method)。即使是对连续表面的定量评估，这些插值方法的准确度也存在较大差异。研究表明，地统计方法优于确定性方法[9]。

确定性插值方法，又称“内插法”，也就是前述的数学插值。确定性是指，观测值只有测量误差，随机性可忽略不计。最简单的确定性插值方法，是求解由比例关系建立的方程，并由此衍生出多项式插值方法。为了让构造的函数既穿过观测点，函数图又形像，人们可将全部数据分割成若干部分，分段插值，再通过最高三阶的多项式，将插值用到的多个函数，尽可能平滑地连接起来。这些用到的函数，就是所谓的“样条”。

确定性插值方法中的反距离加权法，则是假定每个观测点都会存在局部影响，距离较近的事物更相似，因此对于被插值点，距离其越近的观测点影响越大。这种影响的大小，用权值来量化。通过加权求和，进行插值。权值计算方法不同，插值差异很大。最简单的取权值方法，是归一化距离倒数计算权值[10]；复杂一些的，则用到软化参数等[11]。

虽然确定性插值方法的精度不高，但由于简单、易操作，并能起到数据光滑作用，其在地理学中被广泛使用。

地统计方法，不仅仅是将空间坐标点和其地理特征值组成的空间分布，视为一个具有因果关系的随机场，而且认为空间中两个不同点处的取值具有相关性。借用随机过程理论，人们发展出了克里金插值，也译为克里格插值。如果仅仅考虑地统计方法中样本点的随机性，认为样本点具有空间独立性，则可用地理加权回归法来估计空间坐标点和其地理特征值间的因果关系。而通过随机样本训练的后传神经网络(Back Propagation Artificial Neural Network,BP-ANN)，也是一种统计关系。

为本文研究的方便，下面我们简述协同克里金(CollaborativeKriging,CK)插值、GWR和BP-ANN的基本原理和数学模型。为保持这三个模型的传统表述，在不引起混乱的情况下，各模型中的数学符号相对独立。也就是说，同一个符号，在不同模型意义可能不同。

1.1 协同克里金插值

克里金插值是依据协方差函数对随机场进行空间建模和插值的回归算法[12-13]。该方法20世纪60年代产生于地质学界，是一种地质统计学方法，后来被大量用于地理学中，才有了地统计方法的统称。

令集合X由一些空间点x组成。x的三个直角坐标通常记为xu，xv，xw，即，x=(xu，xv，xw); 空间点集合记为{x}，即，X={x}。当一个空间变量Z在x点的取值Z(x)是一个随机数时，称{Z(x)|x∈X}是一个随机场。克里金插值的思想，是将空间参数x视为随机过程中的时间参数t，从而可以使用随机过程中的统计方法，实现插值。

当随机过程的统计特性不随时间的推移而变化时，称为平稳随机过程。具有相应性质的随机场，称为平稳随机场。在平稳随机场中，Z(x)的数学期望E[Z(x)]与其位置x无关。此时，可推导出空间变量Z在某方向上相距h处增量Z(x)-Z(x+h)的方差：

γ(x,h)=Var[Z(x)-Z(x+h)]=E[Z(x)-Z(x+h)]2,

(1)

称γ(x,h)为变异函数，如果与位置x无关，只与距离h有关，此称随机场是二阶平稳的，γ(x,h)可记为γ(h)。

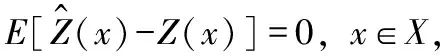
(2)

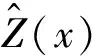
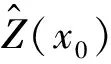
γij=γ(xi,xj)=E[Z(xi)-Z(xj)]2,i,j=0,1,2,…,n。

(3)

使用拉格朗日乘数法[14]求解式(2)，得一个求权向量(λ1,λ2,…,λn)和拉格朗日乘数φ的线性方程组：

(4)

于是，二阶平稳假设下的估计值是：

(5)

式(4)-式(5)称为普通克里金法。外观上看，克里金插值公式(5)与反距离加权法[10]的插值公式完全一样，都是加权求和，但权向量的来源完全不同。克里金法建立在随机过程理论上，而反距离加权法并不考虑随机性。对随机场性质和点之间距离影响程度的理解不同，衍生出了大量的克里金方法。

如果我们不单单考虑空间位置x对随机场的影响，还考虑了其它因素y的影响，但将影响的主次分开，就拓展为特殊的多变量模型[15]，称为协同克里金插值法。例如，水灾灾情，不仅仅是地理空间上的随机场，而且灾情还与地理单元内的GDP、地理单元距河流的距离、地理单元的坡度等众多因素有关。在水灾随机场中，理论上空间位置是主因素，GDP、河流距离和坡度等是次因素，但由于它们紧密的相关性，这些次因素能充分地体现空间位置的随机场属性。

(6)

求解式 (7)的线性方程组：

(7)

被插值点x0的估计值：

(8)

虽然克里金法在地学多领域中有大量成功应用的例子，协同克里金法显著改了精度，ArcMap等软件系统提供了工具模块，但是，通常只在很局部的空间，随机场才满足二阶平稳条件，且一系列弱化条件的改进，也只在很特殊的情况下才有效。因此，协同克里金法并非普适性的空间插值方法。对于空间异质性的问题，地理加权回归更适于空间插值。

1.2 地理加权回归

在统计学中，“回归”是指依据观测样本，对两个或更多变量之间关系性质进行描述，并用于推测。任一回归方法用于地理学问题的研究，都称为地理回归。考虑到样本在各局部空间的统计性质常有明显差异，人们提出了地理加权回归，改进了全局回归。

设x1,x2,…,xm和y分别是空间位置(u,v)观测到的自变量和因变量。对于从n个空间位置(ui,vi),i=1,2,…,n,得到的样本，我们记为：

X={x1,x2,…,xn}={(x11,x12,…,x1m,y1),(x21,x22,…,x2m,y2),…,(xn1,xn2,…,xnm,yn)}。

(9)

当随机变量x的总体是一个m+1维正态分布时，地理加权回归模型是[16]：

(10)

式中：β0(ui,vi)是空间位置(ui,vi)处的截距系数，βj(ui,vi)是(ui,vi)处第j个自变量的局部回归系数，εi为随机误差项。

y服从正态分布时，随机误差ε的期望值为0。此时，对插值点(u0,v0)，从自变量x01,x02,…,x0m，推测因变量，只须根据(u0,v0)与(ui,vi)的远近程度，定义(ui,vi)与(u0,v0)适当的空间权重wi，用它们和X，计算适用于y0的局部系数列矩阵：

(11)

则地理加权回归的推测值由式(12)给出：

(12)

本文中，我们采用式(13)的自适应双平方(Adaptive bi-square)公式[17]来定义wi：

(13)

式中：d0i为(u0,v0)与(ui,vi)之间的欧氏距离。令：

(14)

(15)

(16)

则局部系数列矩阵的计算公式为：

(17)

式中：XT是X的转置矩阵，(XTWX)-1是(XTWX)的逆矩阵。式(12)，式(13)和式(17)构成了自适应双平方GWR插值法。

人们曾用Logistic回归和泊松回归等来探讨改进地理加权回归[18]，试图超越线性回归的限制，但不过是从正态分布假设变为另一种假设而已，并不具有普适性。

1.3 回传神经网络

人工神经元网络能以任意精度逼近任何一个连续函数[19]，为改进地理学中的插值提供了一条新途径。

神经元网络是一个从p维实数空间Rp到q维数实空间Rq的一个映射f:Rp→Rq,并且定义为y=f(x)=φ(Wx)，此处x∈Rp是输入矢量，y∈Rq是输出矢量。W是一个p×q权值矩阵，且φ是一个非线性函数，常称为激励函数。典型的激励函数是S形函数：

(18)

映射f可以分解为多个映射；结果是一个多层网络：Rp→Rm→…→Rn→Rq。

计算W的运算法则是训练算法。最常用的神经网络之一是BP-ANN，算法的基本思想是，学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时，输入样本从输入层传入，经连接各神经元的初始权值矩阵W0处理后，传向输出层。若输出层的实际输出与期望的输出不符，则转入误差的反向传播阶段。误差反传是将输出误差以某种形式通过隐层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正W的依据。周而复始地修正W,直到网络输出的误差减少到可接受的程度，或进行到预先设定的学习次数为止。这种方法也称为自适应模式识别[20]。BP-ANN可视为是用最小期望平方误差作为条件期望函数的一致性估计。

虽然ANN是一个黑箱，但对训练样本不需要任何假设，拟合函数时将空间位置作为输入的一部分即可，避免纠结空间相关性，在地理学中有较好的适应性。例如，可以较大程度地避免生态质量评价时人为主观假定对预测结果的影响[21]，构建植被指数对气候因子响应的复杂关系时拟合优度较高[22]，用于细颗粒物(PM2.5)的估算时短期预测结果更加稳定[23]。然而，ANN却很难成为地理学中通用的插值法，因为宏观数据中有太多的随机、非随机因素干扰，并不存在一个可以逼近的，理论上的连续函数。大多数情况下，训练样本中存在明显冲突，调整权值矩阵W无可适从，训练进入死循环，导致训练后的ANN预测精度并不高[24]。

地理空间上的信息扩散模型，不须对观测样本作任何人为假设，并且能较好地处理样本点之间的冲突矛盾，较好地解决了地理学中常用插值法存在的问题，能有效提高插值精度。

2 地理空间信息扩散技术

在现实中，插值是因为缺失需要的信息。换句话说，只有插值节点间的空白处，才需插值，而插值节点上并不需要插值。拟合并不等于插值。人们对插值模型进行的精度检验，通常是对拟合度的检验。上述CK、GWR和BP-ANN的背后，都是将最小二乘法施于节点处，进行拟合。显然，拟合结果用于推测时，效果都会与拟合点处不同。为了使模型更具说服力，一些研究人员用“训练样本”用来训练模型，留出“验证样本”来展示预测准确性。由于“训练样本”和“验证样本”的选择不同，检验结果很不同，而研究者声称的“随机选择”，很难查实，结果仍然可疑。地理空间信息扩散技术，将插值节点处的信息，向插值点外扩散，直接面对插值需求构造模型。

通信工程中的“信息”，是消除随机不确定性的东西，只有波形的形式因素，没有内容因素，也没有价值因素。现代人工智能理论中，将信息分为客体信息和感知信息。前者是指客体所呈现的关于其自身的“状态及其变化方式”; 后者是指主体从客体信息所感知的客体状态及其变化方式的形式、内容和效用[25]。地理空间信息扩散技术中，插值节点处的观测值，是人们已经感知到的信息；模型试图推测的，是插值点外的客体信息。

信息扩散，是将观测点的感知信息，扩散到非观测点，力图对非观测点有所认识。信息扩散，是人类用有限的知识，认识无限世界的本能。信息扩散不同于联想，并不是由于某人或某种事物而想起其他相关的人或事物；信息扩散，也不是信息传播，并非是个人、组织和团体通过符号和媒介交流信息。近年来，许多文献将“信息传播”称为“信息扩散”，旨在借用大量的数学工具，但内涵并没有变化。

地理空间信息扩散技术来自于优化处理小样本的信息扩散原理[26]：当我们用一个不完备数据估计一个关系时，一定存在合理的扩散方式可以将一个没有几何大小的观测值变为一个集值(例如，模糊集)，以填充由不完备性造成的部分缺陷从而改进非扩散估计。该原理不仅在概率空间中成立，而且在几何空间中也成立[27]。这就意味着，我们可以将信息扩散技术，拓展到在地理空间上去，以填补地理单元上的数据空白，使不完整的空间数据集，变为完整的数据集。

然而，概率空间中的信息扩散方法，并不能直接用于地理空间，而须借助在观测点和非观测点都有的同类背景数据作为桥梁[2]，才能将观测点的感知信息，扩散到非观测点。为此，我们先界定两个基本的概念：“空白单元”和“背景数据”。

2.1 空白单元和背景数据

定义1：设g和o是研究区域G中的两个地理单元。如果在识别G上的地表现象F时，g被观测并被赋值，而o没有，则对于识别F而言，称g是一个被观测单元，o是一个空白单元。

例如，在洪水灾区，灾情是一种临时的地表现象，已经被调查过灾情并获得数据的地理单元，是被观测单元；没有被调查过灾情的地理单元，是空白单元。

对地理单元g的观测值(或向量)wg称为一个已观测数据；对空白单元o的相应值(或向量)wo，称为一个待观测或待推测数据。设bg1,bg2,… ,bgt和bo1,bo2,… ,bot分别是g和o的t个同类地理特征的属性值。记向量bg=(bg1,bg2,… ,bgt),b0=(bo1,bo2,… ,bot)。

定义2：设g1,g2,…,gn是n个被观测单元，o是一个空白单元，它们的属性值向量集合是B={bg1,bg2,…,bgn,bo}。如果能用B依据观测数据wg1,wg2,…,wgn推测wo，称B为背景数据集，简称背景数据。

例如，用“人口”、“人均GDP”和“相对暴露度”等数据，依据被观测单元的灾情，推测空白单元的灾情时，“人口”、“人均GDP”和“相对暴露度”等就是背景数据。此时，空间位置已经在计算“相对暴露度”时发挥过作用[28]。

任何能用背景数据，由多个被观测单元的观测值，推测空白单元上相应值的方法，都具有将被观测单元的信息扩散到空白单元的功能。例如，CK、GWR和BP-ANN等插值方法，都具有某种信息扩散的功能，但并不明显，因为这些模型的控制规则，不是为了填补空白，而是为了最佳拟合。

设研究区域G由n-q个被观测单元g1,g2,…,gn-q，和q个空白单元gn-q+1,…,gn组成，即，

G={g1,g2,…,gn-q,gn-q+1,…,gn}。

(19)

设背景数据由t个地理特征的属性值组成。记地理单元gi第j个特征的属性值为bij，i=1,2,…,n;j=1,2,…,t。将wgi简记为wi，i=1,2,…,n，于是，关于G上的信息可由表1示之。

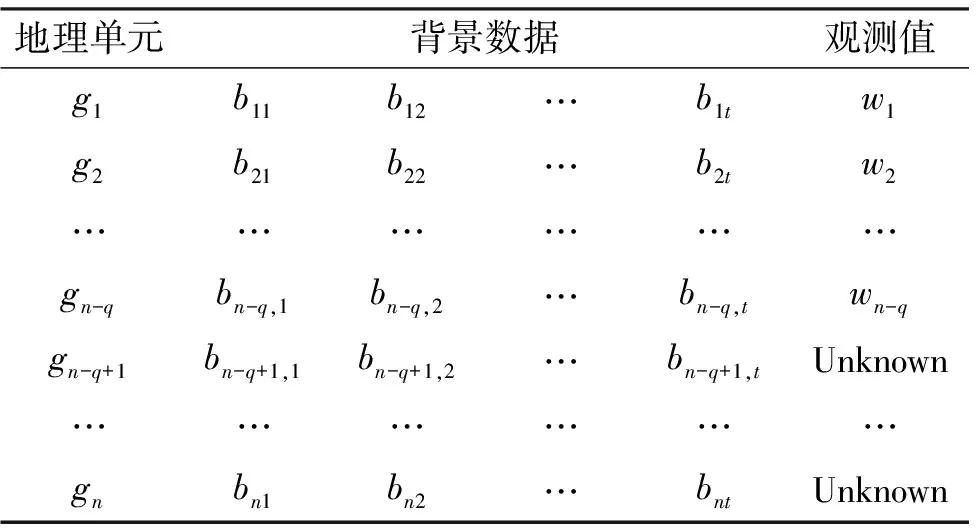
表1 研究区域G上的观测值和背景数据

以背景数据bij为桥梁，在地理空间G上进行信息扩散的方法，由构建因果关系矩阵和模糊近似推理两部分组成[2]。

2.2 用背景数据和已观测数据构建因果关系矩阵

令τ=n-q，λ=t+1，我们从表1中得到容量为τ的λ维样本X：

X={(xi1,xi2,…,xiλ-1,xiλ)|i=1,2,…,τ}。

(20)

式中：xi1=bi1,xi2=bi2,…,xiλ-1=bit,xiλ=wi,i=1,2,…,τ。

设Uj,j=1,2,…,t,是用于扩散背景数据中第j个地理特征属性值的监控空间，而Ut+1是用于扩散已观测数据的监控空间。令λ维笛卡尔空间：

U=U1×U2…×Uλ。

(21)

式中：Uj={uj1,uj2,…,ujmj},j=1,2,…,λ。理论上，对不同的分量j，监控点的个数mj可以不同，但由于监控点的密度达到一定程度后，用不同的mj并不影响插值的精度，因此，我们取一个m作为所有分量监控空间中监控点的个数。

对于任意一个样本点，

xi=(xi1,xi2,…,xiλ)∈X,

(22)

和任意一个监控点，

u=(u1k1,u2k2,…,uλkλ)∈U,kj∈{1,2,…,m},j=1,2,…,λ。

(23)

我们用式(24)的λ维初级扩散公式，将x的信息扩散到u。

(24)

根据表1中的背景数据和已观测数据，分别用式 (25)计算扩散系数hj,j=1,2,…,λ。

(25)

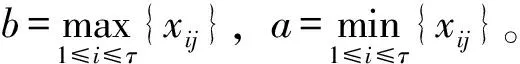
令：

(26)

此数值表征了样本X在监控点u处的密集程度，可用于改进扩散模型，得到适应性扩散模型[29]：

(27)

于是，我们获得了一个U1×U2…×Uλ上的，关于X的信息矩阵：

Q={Qk1k2…kλ-1kλ}m×m×…×m。

(28)

∀j∈{1,2,…,λ}，kj∈{1,2,…,m},令：

(29)

和

(30)

此为针对分量j的归一化信息矩阵中的元素，此矩阵记为：

(31)

我们可由X构造出一个背景数据与观测数据之间的因果关系：

(32)

此因果关系矩阵中的元素为：

(33)

式(29)-式(32)的关系矩阵生成法，来自于模糊蕴含理论，适用于由小样本生成，离散性较大的原始信息矩阵Q(式(28))。如果样本较大，Q的元素值呈现出一定的统计规律，可直接将Rλ作为关系矩阵使用。对所有归一化信息矩阵进行的取小运算，具有滤波的作用，也会丢失少量的统计信息。

2.3 用背景数据推测空白单元中未知数据

设b=(b1,b2,…,bt)为表1中一个空白单元的背景数据，λ-1维笛卡尔空间U1×U2×…Uλ-1中的一个点记为uλ-1=(u1k1,u2k2,…,uλ-1kλ-1)。用式(24)中用到过的扩散系数h，由式(34)将b变为论域U1×U2…Uλ-1上的一个模糊集，并用式(35)进行归一化处理。

(34)

(35)

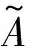
(36)

(37)

最后，使用式(38)的信息集中法[32]，我们获得了一个分明值w：

(38)

当Rλ可以作为关系矩阵使用时，用重心法[8]替代信息集中法，精度更高。

由公式(24)-式(38)组成的模型，称为自学习离散回归(Self-Learning Discrete Regression,SLDR)模型，是一种地理空间信息扩散技术。式(38)中的w是使用此技术，由空白单元的背景数据b和从被观测单元学习到的因果关系R，对空白单元的插值。

一个由“人口”、“人均 GDP”和“洪水相对暴露度”推测“洪水损失”的计算机仿真实验证明，在拟合精度上，SLDR模型明显优于GWR和BP-ANN，误差分别降低了60%和33%左右[8]。对空白地理单元“洪水损失”的推测，SLDR和BP-ANN通过了平均基准误差小于平均预测误差的检验，证明了SLDR和BP-ANN插值的效性，而GWR无效[30]。此检验中，基准误差是指，给定样本除去一个测试点后模型的均方根误差；预测误差是指，测试点的实际值与估计值之间的误差。样本中的每一个点均担任一次测试点任务，形成的平均误差用于检测插值的有效性，避免了使用主观“验证样本”存在的问题。

本文将以2018年和2020年发生在四川省三台县的两次大洪水的水灾灾情为例，实证研究地理空间信息扩散技术的可靠性，为从理论走向实践，进行必要的探索。

3 研究区概况

我国三分之二以上的国土面积受到洪涝灾害威胁，主要分布在长江、黄河、淮河、海河、珠江、松花江、辽河7大江河下游和东南沿海地区。这些大区域的水灾，相邻的较小地理单元上，灾情的同质性很高，只有进行大范围的调研，获得的数据才能支撑水灾插值模型的研究。为此，我们选用小范围内差异较大的四川省三台县涪江流域麦冬主产区作为实证研究区域。由于发生在当地的洪水具有一走一过的特点，涝灾并不明显，所以本文只研究洪水灾害的插值问题。

四川省绵阳市三台县位于四川盆地中部偏北，30°42′34″～31°26′35″N，104°43′04″～105°18′13″E；属于亚热带季风气候区，年平均降水量为876.2 mm，降水在年内和年际变化大，年降水集中在夏秋两季，其中6—9月降水量占全年降水量的72.4%；境内地质构造简单，全部由褶皱构造组成，无地质断层，海拔高度307 m至672 m。属川中丘陵地区，地势北高南低。县境内大小江河溪流46条，均属于长江支流嘉陵江水系，其中涪江、凯江、梓江、郪江为四条大江。涪江由绵阳市涪城区丰谷镇进入三台县境内，经永明、芦溪、老马、刘营、里程、灵兴、新德、潼川、北坝出境至射洪县香山镇。

三台县历来易受洪水灾害影响。据历史资料记载，从唐贞观十八年(644)到民国三十八年的1 300年中，三台发生严重的暴雨洪涝灾害计38次，其中有19次县城被淹。1949年 10月新中国成立后，共计出现洪水灾害31次，其中特大洪灾6次。截至2018年，近30%的涪江沿岸地段还暴露在无堤防状态下。

三台县幅员面积2 659 km2，丘陵面积占94.39%，2021年辖31个镇、2个乡，总人口139.12万，其中农业人口123万。2020年，生产总值407.45亿元，经济发展程度较高，是我国最大的生猪产地县。三台县享有“中国麦冬之乡”的美誉，麦冬产业带覆盖了芦溪镇、永明镇、老马镇、建设镇、刘营镇、灵兴镇、新德镇等乡镇，气候、湿度、土壤均适合麦冬生长，有500多年种植麦冬的历史，其“涪城麦冬”居全国麦冬之上品，目前三台全县常年种植麦冬面积达3 333 hm2，年均产量1.2万t，占全国的70%以上，麦冬出口量占全国的80%以上。

2018年7月和2020年8月，三台县发生了大洪水，涪江流域的永明镇、老马镇、刘营镇、灵兴镇受灾尤其严重，当地民众对灾情记忆犹新，为此，我们选择了这四个镇作为实证研究区域，其地理位置由图1所示。

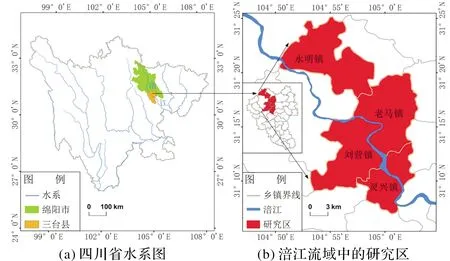
图1 实证研究区域的地理位置(基于自然资源部标准地图服务网站审图号为GS(2019)1821号的标准地图制作，底图无修改)

4 近年两次大洪水概况

4.1 2018年“7·11”特大洪水

2018年7月9-11日涪江流域上游县市区的强降雨和局地的大暴雨使得涪江、凯江、梓江、魏城河、郪江遭受了建国以来最大洪峰的洗劫。尤其是三台县涪江、凯江水位极速大幅上涨，流量均为历史最大峰值。

洪水期间，永明镇和花园镇(2019年划归芦溪镇)等40个镇乡受灾，受灾人口达25.1万人，实施紧急转移安置21 562人，集中安置1 612人、分散安置19 950人，由于沿江的镇乡党政对于群众的疏散转移有效及时，无人员死亡。

涪江流域“7.11”特大洪水，导致三台县境内的道路、堤防、水库、渠系、电力、供水、通信、能源等基础设施毁损严重。洪水冲垮了2 000 m多的土堤造成决堤，有50 km多的基础设施需维修加固或重建，有3条县内公路中断，3座大桥临时交通安全管制。全县水利工程2 324处受损，直接损失4.2亿元。江河干流堤防决口9处、损坏工程护岸145处，有14座水库管涌产生新的病险。2条电力干线受损，导致19个镇乡突然停电。基础设施毁损5亿余元。其中，芦溪工业区殷家壕堤防、花园镇涪城村护堤、里程镇回龙村堤防和刘营镇下渡口堤防瞬间决堤导致洪水灾情最为惨重。芦溪工业区的大量厂房被淹，物料、机器、设备被洪水浸泡，损毁惨重，造成24户重点工业企业毁损、停产，直接工业损失达6.3亿元。

此次洪水共造成社会经济损失近18亿元，其中，农林水产受灾19 442 hm2，其中绝收2 077 hm2，农田(含鱼塘)毁损198 hm2，农业直接损失3.8亿元。

4.2 2020年“8·12”大洪水

2020年8月11—12日，涪江流域普降大到暴雨，上游的安州、北川、平武局地降下特大暴雨，洪灾压力加之疫情防控的重担，为三台县带来了70年来最为严峻的大考。

三台县于8月11日启动并迅速提高至Ⅲ级防汛预警响应，16日启动II级防汛应急响应。期间，涪江中下游超保证水位1.8 m，13 000 m3/s的洪峰冲击导致明台库区尾段的新德镇马脊防洪堤基脚被洪水掏空100 m左右，出现了560 m迎水面“垮方险情”，省县部门紧急加固抢修，最终保证了洪峰顺利过境。

由于人员转移安置及时，抗洪抢险行动到位，全县此次洪灾并无人员伤亡情况。但极端降水重创了交通基础设施，造成三台县境内道路路基垮塌、山体塌方严重，出现1 433处灾毁险情，其中：国道16处、省道199处、县道75处、乡道193处、村道950处。中立路永明镇涪建村段受灾最为严重，车辆、群众出行受阻。因灾损毁道路于当月月底全部抢通。水路设施方面，共计受损5个渡口以及两岸码头。

5 灾区背景数据和灾情数据

为了研究三台县的洪水和地震灾害综合风险，2017年北京师范大学与三台县合作建立了“安全科学与工程”教学实践基地，2018年和2020年，分别对“7·11”特大洪水和“8·12”大洪水进行了一些调研。2021年6月17—20日期间，本文作者前往研究区，对研究区的25个村庄进行了野外考察和入户调查，获得了第一手资料。根据调研村庄的海拔与水文特征(图2a)、土地利用情况(图2b)及坡度计算结果(图2c)，经过整理和分析，我们得到了对地理空间信息扩散技术进行实证研究所需的背景数据(表2)和灾情数据(表3)。每一个地理单元g获得3个背景数据“与河流距离”、“GDP”和“坡度”，其中，“坡度”(bg3)，是用拟合曲面法[31]由ArcGIS平台计算而得。

图2 调研区域水灾背景数据分析资料及调研村庄的地理位置注：海拔来源于ASTER GDEM V2 全球高程数据；水系数据由全国1∶25万地理信息数据库与县水利局河流水系平面图整理得到；土地利用资料来源于Esri提供的2020年10 m分辨率土地利用数据(https://www.geoscene.cn/)。

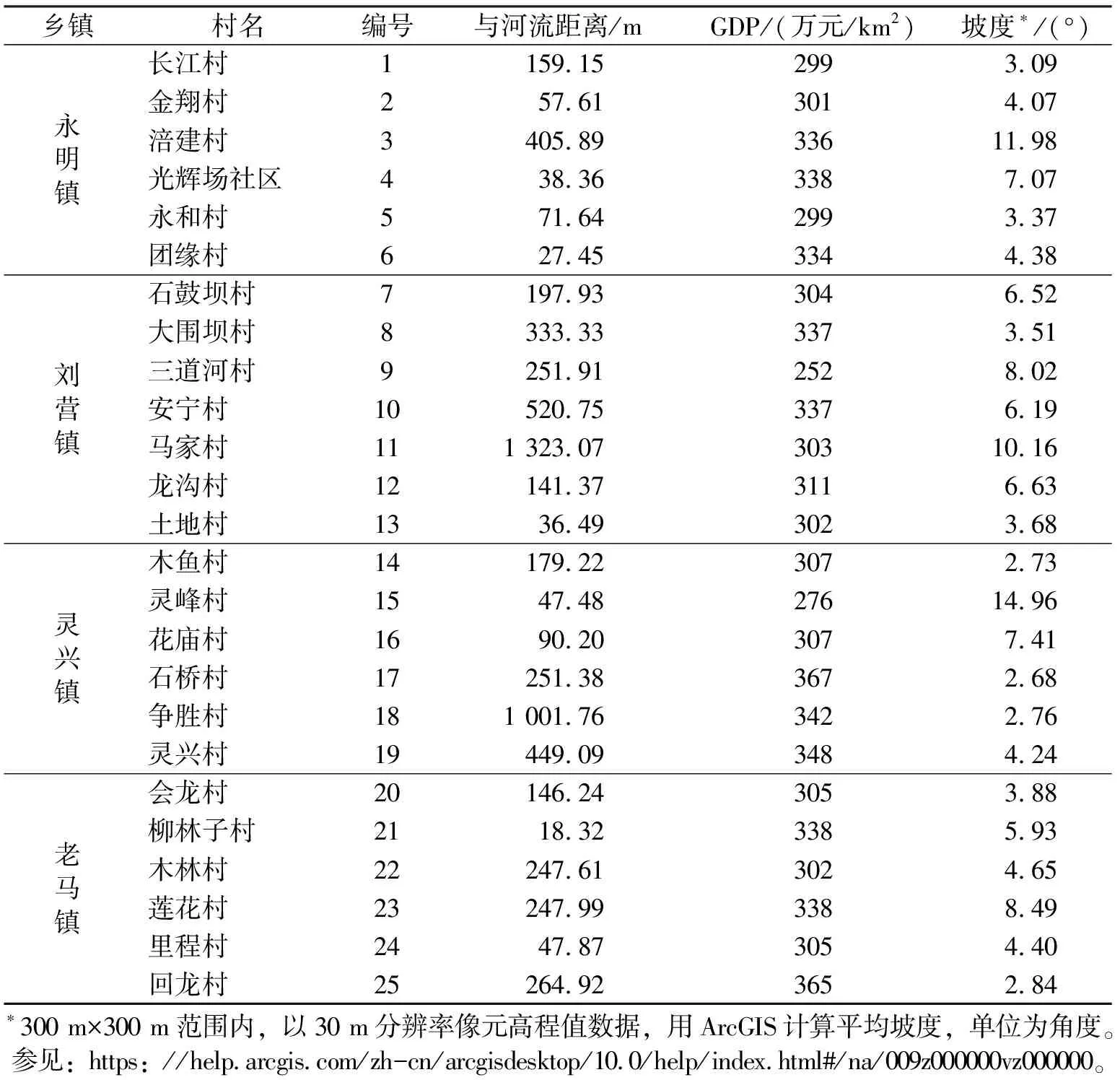
表2 研究区25个村庄的背景数据

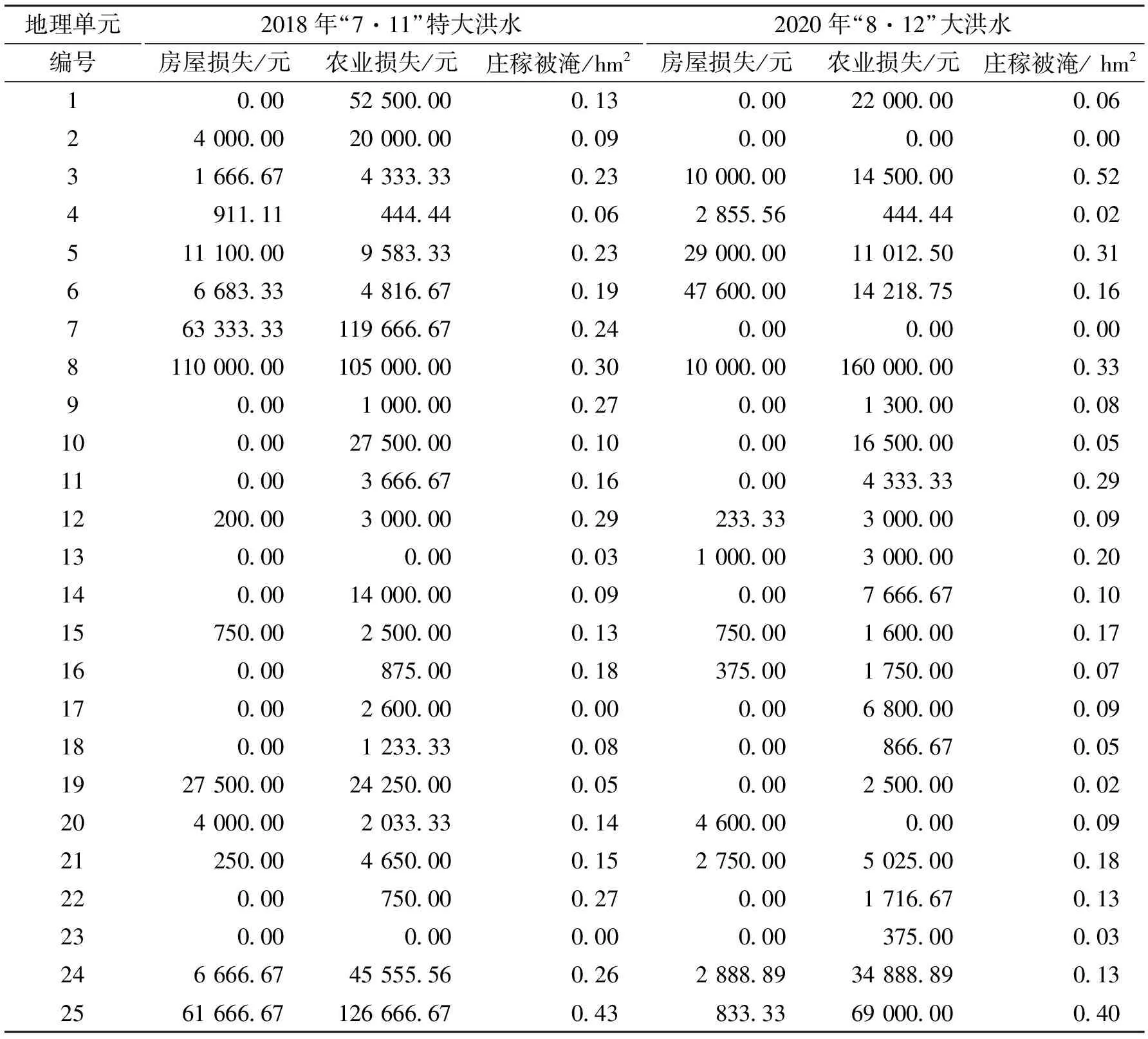
表3 两次大洪水的灾情数据

6 用信息扩散技术推测灾情

我们以2018年“7·11”特大洪水中农业损失为例，演示如何用信息扩散技术构建因果关系矩阵，由背景数据推测灾情。然后，通过模型对全部3种灾情的预测误差分析，说明其插值是有效的。

6.1 构建因果关系矩阵

由表2中的背景数据和表3中的第3列数据，我们得到容量为τ=25，维度λ=4的样本X：

(39)

根据表2中河流距离、GDP、坡度和表3中农业损失的最大值和最小值，并依据样本容量大小，我们以等步长方式，各取20点构成它们的监控空间，即：

(40)

我们以式(39)中的第1个样本点

x1={x11,x12,x13,x14}=(159.15,299,3.09,52 500)

(41)

为例，演示如何将其信息扩散给4维笛卡尔空间U1×U2×U3×U4中，与其距离较近的两个点：

u18407=(u13,u27,u31,u47)=(155.66,288.32,2.68,40 000);

和

u18408=(u13,u27,u31,u48)=(155.66,288.32,2.68,46 666.67)。

笛卡尔空间点的编号，是按矩阵元素的序号排法所得。首先，由式(25)处理式(39)的样本数据，可得各分量的扩散系数h1,h2,h3,h4分别是145.974,12.866,1.374和14 171.362。于是，

=1.000×0.708×0.956×0.678

=0.459;

(42)

=1.000×0.708×0.956×0.919

=0.622;

(43)

将式(39)中的所有25个样本点，在U1×U2×U3×U4上完成初级扩散并累加后，我们得到一个初级信息分矩阵S={Sk1k2…k4}20×20×20×20，例如u18407和u18408上获得的初级信息扩散总量分别是S3,7,1,7=0.841,S3,7,1,8=0.868。由式(37)进行适应性扩散，我们得到一个原始信息矩阵Q={Qk1k2…k4}20×20×20×20例如u18407和u18408上获得的适应性扩散总量分别是Q3,7,1,7=0.813,Q3,7,1,8=0.838。对X的信息矩阵Q，我们从第1分量到第4分量，分别进行归一化处理，得到相应的归一化信息矩阵。例如，对第4分量，即“农业损失”，k4=7和k4=8时，我们分别有：

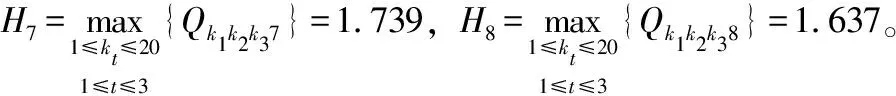
(44)

于是，

(45)

由式(32)对4个归一化信息矩阵进行“取小”运算，可得该地区此次洪水事件中，得到“农业损失”与“与河流距离”“GDP”、“坡度”因果关系的一个估计R。例如，在此因果型关系矩阵中我们有：

(46)

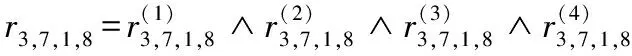
(47)

比较这两个元素的值可知，输入u=(u13,u27,u31)时，“农业损失”是u47(=40 000元)的可能性比u48(=46 666.67元)的小。

6.2 用背景数据推测灾情

我们以背景数据b=(b1,b2,b3)=(159.15,299,3.09)为例，用6.1节中构建的因果关系矩阵，推测农业损失。选用的背景数据是式(41)中x1的前3个分量。推测的是长江村2018年“7·11”特大洪水中的农业损失。

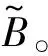
(48)

(49)

式中:uk1k2k3是U1×U2×U3中点(u1k1,u2k2,u3k3)的简写。例如：

=1.000×0.708×0.956

=0.677。

(50)

(51)

例如a371=0.677/0.979=0.692。使用近似推理公式(37)，我们得到模糊输出：

(52)

需注意上式并非分数求和，而是模糊集的扎德记法。该模糊输出表达的是：损失为0元，6 666.67元，…,126 666.65元的可能性分别是0.885,0.952,…,0.161。使用式(38)对此模糊集进行信息集中处理，我们得到由背景数据(159.15,299,3.09)推测的农业损失是：

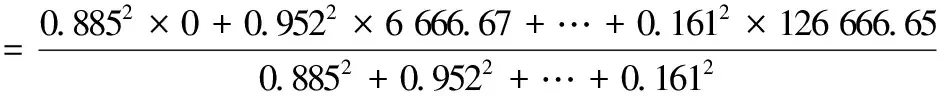
=22 053.27(元)。

(53)

6.3 预测误差分析

由背景数据 (159.15,299,3.09)，用地理空间信息扩散技术的SLDR模型推测的，长江村2018年“7·11”特大洪水中的农业损失，是22 053.27元，与表2中观测值52 500有较大的出入，这是由于25个样本点的灾情标准差高达37 448.98所致。通常，我们用均方根误差，来比较两个模型拟合插值节点的误差。但拟合得很好的模型，不一定适合于节点以外的插值。只有节点以外的预测误差，才能体现插值精度[30]。

为了区分样本点中的自变量和因变量，我们将式(20)中的样本改写为

(54)

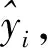
(55)

令：

E={1,2,…,τ}。

(56)

∀η∈E，令：

(57)

称XLη为训练样本(有τ-1个样本点)，称Xη为测试样本(只有一个样本点)。显然X=XLη∪Xη。由XLη训练模型f，其均方根误差称为f的一个基准误差，记为σLη；f对yη的预测误差，称为f的一个预测误差，记为eη，即

(58)

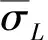
(59)

对表2和表3给出的数据，SLDR模型的均方根误差、基准误差和预测误差见表4。

根据文献[30]的研究，一个模型的预测是否有效，须通过两个准则来检验。

准则I：平均基准误差必须小于平均预测误差，确保模型能从此样本中总结出规律。

准则Ⅱ：平均预测误差较小，确保模型的精度。

如果基准误差大于预测误差，就相当于说，你游历了欧洲而不是非洲，但是你对非洲的描述比欧洲更准确，这显然是荒谬的。如果基准误差明显大于预测误差，说明模型不符合逻辑，对给定样本的学习无效；或者说，使用的模型与给定的样本不匹配。表4中，3个案例的基准误差小于预测误差，另3个案例的预测误差没有明显小于基准误差，说明SLDR用于学习相应6个样本是有效的，具有普适性。至于SLDR的预测误差是否较小，须同别的模型进行比较，才能显现出来。

7 与CK、GWR和BP-ANN模型的比较

分别用CK、GWR和BP-ANN模型对表2和表3给出的数据进行处理，所得结果列入表5、表6和表7。由表4比较这三个表可知，就本文的实例而言，只有SLDR模型能够通过预测有效性两个准则的检验。CK模型的预测误差均明显小于基准误差，通过不了准则I的检验，插值无效。在5个案例中，GWR模型的预测误差，均明显小于基准误差，也不合逻辑，插值无效。

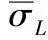
表4 自学习离散回归模型(SLDR)均方根误差σ、基准误差和预测误差

表5 协同克里金模型(CK)均方根误差σ、平均基准误差和平均预测误差

表6 地理加权回归模型(GWR)均方根误差σ、平均基准误差和平均预测误差

表7 回传神经网络模型(BP-ANN)均方根误差σ、平均基准误差和平均预测误差

表7中，BP-ANN采用3×9×1拓扑结构，学习系数0.9，惯性系数0.7，系统误差0.000 9。例如，用2018年“7·11”特大洪水时25个村庄的背景数据和农业损失组成的样本，训练出的神经网络，拟合的均方根误差是6 678.87元(见表7第3行第3列)。而从25个村庄中随机地取24个的数据组成样本训练网络时，一些样本的训练进入死循环，拟合的均方根误差较大；一些样本能顺利完成训练，均方根误差较小，平均基准误差为12 645.68元(见表7第4行第3列)。用24个村庄的数据训练出的网络对没有参加训练的村庄进行插值(预测)时，平均预测误差高达82 681.68元(见表7第5行第3列)。

对所有6个案例，BP-ANN模型的基准误差均小于预测误差，通过了准则I的检验，但没有通过准则Ⅱ的检验，因为其预测误差远远大于SLDR、CK和GWR模型，精度太低，是一个无效的预测模型。这一现象说明，能够高度拟合训练样本的回传神经网络模型，并不适用于复杂地表现象的插值。

8 结论和讨论

由于成本和时效等诸多原因，用插值来完善地理空间数据，具有重要意义。在满足相应条件的情况下，许多插值模型都可以使用。但是，常用的插值模型，都不具有普适性。

虽然内插式的数学插值模型精度很高，但只适用于空间连续场；克里金法和地理加权回归等地统计方法考虑到了空间数据的随机性，但只适用于有大样本支撑的插值；回传神经网络模型能够高度拟合训练样本，但插值精度可能并不高。

模型的拟合精度高，并不等于插值精度也高。插值是因为缺失需要的信息，只有插值节点间的空白处，才需插值，节点上拟合并不是插值。插值是对空白处有关数值的预测。因此，一个模型是否可通过某样本的训练有效地进行插值，可通过两个准则来检验，一是平均基准误差必须小于平均预测误差，确保模型能从此样本中总结出规律；二是平均预测误差较小，确保模型的精度。

本文以2018年和2020年发生在四川省三台县的两次大洪水，造成25个村的房屋损失、农业损失和庄稼被淹等三类水灾灾情数据组成的6个案例，实证了地理空间信息扩散技术能通过两个准则的检验，是普适性插值模型。协同克里金模型在所有案例中，都没有通过准则I的检验，不合逻辑，说明插值无效；地理加权回归模型在5个案例中没有通过准则I的检验。虽然回传神经网络模型通过了准则I的检验，且基准误差很小，但预测误差却比基准误差高出近一个数量级，也比自学习离散回归模型、协同克里金模型和地理加权回归模型的预测误差都大很多，没有通过准则Ⅱ的检验。这说明，回传神经网络模型并不适用于复杂地表现象的插值。

信息扩散的自学习离散回归模型，是一种以离散数学表达的数学模型，能充分发挥现代计算机大容量存储、高速度运行的功能，具有某种人工智能的属性，如果能在扩散方式和近似推理等方面进一步完善，有望为地理空间插值提供一个重要的工具。