变截面隧道与典型缓冲结构气动效应缓解效果对比分析
2022-06-26李文辉刘堂红周苗苗郭子健夏玉涛
李文辉,刘堂红,周苗苗,郭子健,夏玉涛
(1.中南大学交通运输工程学院,轨道交通安全教育部重点实验室,湖南长沙,410075;2.中南大学轨道交通安全关键技术国际合作联合实验室,湖南长沙,410075;3.中南大学轨道交通列车安全保障技术国家地方联合工程研究中心,湖南长沙,410075)
当列车高速进入隧道时,由于空间受到隧道洞壁和车身的限制,所诱发的马赫波在洞内不断传播、叠加而形成复杂波系[1]。这种空气动力学效应将诱发一系列问题,如:司乘人员耳膜不适引起乘车舒适性体验变差[2];长期交变压力载荷导致车辆、隧道产生疲劳破坏[3-4];隧道内列车风、阻力、隧道内热量积聚和温升等[5]。上述隧道气动效应是影响新建高铁隧道或既有线提速改造的瓶颈问题之一,因此,亟待寻求新型措施以便有效缓解隧道气动效应。减缓隧道气动效应问题的工程措施主要包括车体优化和隧道改造2 个方面[6]。前者包括提高列车密封性及增强车头流线化设计,如周细赛等[7]对不同主型线头部列车隧道交会气动效应进行模拟,发现单拱型列车隧道交会气动性能比双拱型的列车隧道交会气动性能略优。KU等[8]以减小隧道微气压波为目标,通过数值仿真和优化算法对高速列车头部形状进行了优化。潘美风[9]以CRH380 型高速动车组气密性为例,提出了等效泄漏面积顶层指标的金字塔分解方法。隧道改造方面则包含增设洞口缓冲结构、洞内辅助设施等。如闫亚光等[10]比较了10 种缓冲结构对初始压缩波峰值和最大压力梯度的减缓效果,发现缓冲结构减缓初始压缩波峰值并不明显,长度为20 m、开2 个孔的缓冲结构的减缓效果最佳。HOWE 等[11]基于声学理论分析了多开口缓冲结构对隧道气动效应的缓解效果,并对其布置位置、尺寸等参数进行了优化。王英学等[12]采用三维数值研究了横通道设置对压力波传播特性的影响,对不同位置设置横通道缓解微气压波的效果进行了比较。列车流线型优化设计对减缓隧道气动效应程度十分有限,而提高列车气密性标准将大幅增加运营成本,故在保证列车运能和运营成本不变的情况下,最为经济、有效的工程措施是采用洞口缓冲结构[13]。缓冲结构可以从源头上减小列车突入隧道时形成的马赫波的强度与梯度,但缓冲结构受隧道口地形等条件的限制(如桥隧相连等地形不适宜或无空间修缓冲结构)。另外,受隧道外环境条件的限制,缓冲结构的长度等参数必须控制在一定范围内,因而,对隧道气动效应特别是隧道内压力变化的缓解效果有限[10]。
从以上分析可知,国内外对隧道气动效应的研究大部分是针对等截面隧道,而针对隧道截面变化时气动效应问题的研究主要集中在以下几个方面:在隧道增设缓冲结构[14-15]、横洞或竖井等辅助设施[16-17];隧道内有分支;隧道内有开口或隔墙[18];病害防治增设衬套[19];地铁隧道遇到站台等引起截面变化[20]。列车通过隧道断面突变结构形成环状空间内部,流体的流动形态和压力波的传播更加复杂[21]。刘峰等[22]采用三维、可压缩、非定常求解N-S方程的数值计算方法,对8车编组的高速列车以300 km/h 时速通过带有衬套的隧道内瞬变压力进行了分析,发现加装衬套对于隧道气动效应影响较小,最大压力幅值差异在2%以内,因此,在隧道病害防治中可采纳衬套技术。程爱君等[19]对动车组以300 km/h 和350 km/h 速度通过长度为800 m、中间断面由100 m2减为93 m2的变截面隧道的工况进行研究,发现瞬变压力和洞口微气压波能满足相关标准要求。LIU等[23]采用实车试验、数值模拟、动模型试验等,对8车编组的高速列车以不同速度通过不同位置带有衬套结构的隧道时洞口微气压波进行分析,发现衬套改变了隧道断面积,对洞口微气压波有较大影响。
综上可知,国内外对隧道气动效应减缓措施研究多集中于等截面隧道,而变截面隧道的已有研究主要是针对隧道病害防治、隧道施工通风等被动改变隧道截面的情况,其初衷并非专门减缓气动效应。为此,本文设计一种保持隧道出入口断面积不变而在内部采用较小断面的隧道形式,并将其与典型缓冲结构对隧道气动效应的缓解效果进行对比研究,以期为桥隧相连、地形复杂等无法外置缓冲结构的环境提供新型隧道形式的设计思路,从而达到缓解隧道气动效应和降低线路工程造价的目的。
1 数学模型
列车以时速U=350 km/h 高速进出隧道,由于洞内空气受到壁面限制和列车车头挤压,尽管马赫数略小于0.3,仍需将洞内气流视为三维可压缩流动[24],同样遵循质量守恒定律、动量守恒定律和能量守恒定律,因此,整个流场采用三维、可压缩、非定常雷诺时均方程(URANS)和工程上应用广泛的RNGk-ε双方程湍流模型求解[25]。采用流体计算软件ANSYS FLUENT 19.2对场景进行模拟计算,时间步长取0.005 s,采用SIMPLE算法求解速度压力耦合方程,对流项和扩散项则采用二阶迎风格式离散,时间项采用二阶隐式。流体控制方程及湍流模型见文献[26]。
2 数值方法
2.1 计算模型
变截面隧道设计思想为:进出口两端保持较大断面,中间段主隧道采用较小断面,见图1(a)。扩大段的净空有效断面保持我国既有高速铁路最大断面S1=100 m2不变,扩大段延伸长度L1=100 m;中间段主隧道根据我国200 km/h 速度等级客货共线双线隧道断面标准,采用较小截面S2=80 m2,隧道总长度Ltu=1 000 m。动车组模型采用8 车编组CRH380A 即头车、六节中间车与尾车的常规编组,忽略受电弓、道砟和轨道并合理简化底部转向架结构,如图1(b)所示。其具体几何参数为:车宽W=3.38 m,车高H=3.7 m,总长度Ltr=203 m,平直段横截面积Str=11.2 m2。线间距为5.0 m,轮对最低点离地间隙0.2 m,车速U=350 km/h。模型采用大地参考坐标系,原点位于隧道入口处,其中x轴沿隧道纵向,y轴和z轴分别代表横向和垂向。
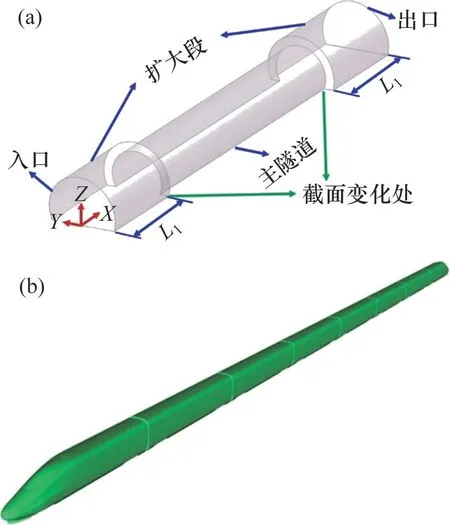
图1 隧道及列车模型Fig.1 Models of tunnel and train
为减小列车/隧道耦合空气动力学效应,工程设计人员经常采用洞门缓冲结构(如棚洞、明洞),其净空断面积大于隧道净空有效面积。本文基于Ltu=1 000 m的80 m2等截面隧道,分别在隧道入口设置断面扩大型、断面扩大开孔型共2种典型缓冲结构,缓冲结构断面积为隧道断面积的2 倍即160 m2,缓冲结构长度为20 m[4],开孔型缓冲结构在顶部开了2个大小一致(长×宽均为4 m×3 m)的泄压孔(开孔率为0.3),将这2种缓冲结构与上述变截面隧道气动效应缓解效果进行对比分析。图2所示为2种缓冲结构的三维模型示意图。
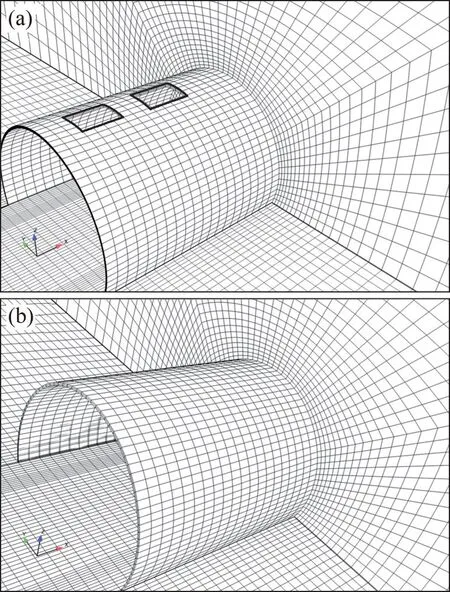
图2 隧道缓冲结构模型Fig.2 Models of tunnel hoods
2.2 计算域、网格及边界条件
采用滑移网格法模拟列车与隧道之间的相对运动[21]。如图3所示,采用2个相同的长×宽×高为500 m×120 m×60 m 的立方体模拟隧道外域。列车放置于运行方向的左侧轨道,初始位置距隧道入口50 m。为保证列车突入隧道流场的稳定性,列车鼻尖在隧道外运行时间为t0=0.51 s。将整个计算区域划分为滑移区域和固定区域,滑移区域包裹着整个列车以车速运动。在固定区域中,隧道表面和地面均设置为无滑移壁面,其余均设置为压力出口。滑动区与固定区的接触面设置为交界面以交换运动过程中二者的流场信息。
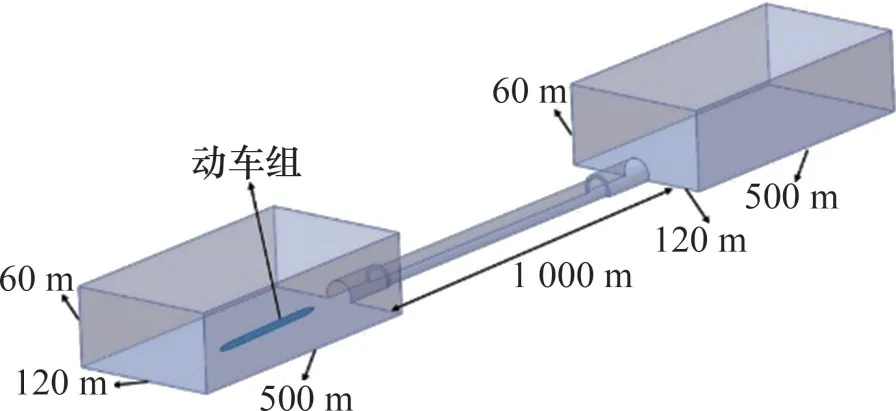
图3 数值模拟计算域Fig.3 Computational domain
由于列车模型包含流线型曲面及转向架等复杂结构,因此,选择混合网格对计算域进行离散。y=2.5 m 时计算域的切片网格分布如图4 所示,其中,列车的滑移区域采用四面体网格进行离散,剩余滑移区域采用棱柱网格离散,固定区域则以六面体网格离散。整个计算区域网格单元总数约为3 900万个。明线运行的前10步计算设定为不可压缩流动,之后改变空气属性为可压缩流动,列车在隧道内运行时间约为t=t0+(Ltu+Ltr)/U=13 s,由于网格数量较大,采取并行计算,计算数据通过FLUENT用户自定义函数(UDF)输出,所有计算都在国家超级计算中心(NSCCWX)完成。

图4 计算域切片网格分布Fig.4 Plane mesh distribution of the domain
2.3 测点布置
由于列车运行在左侧轨道,洞壁左侧更靠近列车车体,瞬变压力变化比右侧压力变化更加剧烈[21],因此,本文隧道压力测点均布置在距离地面4.2 m处的左侧洞壁,共13个,如图5所示,以全面研究列车通过变截面隧道洞壁压力时空分布情况。
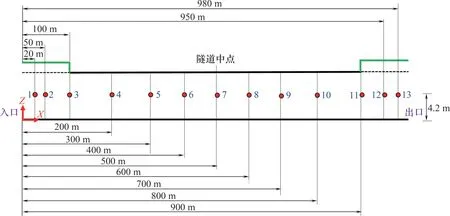
图5 隧道洞壁压力测点分布Fig.5 Distribution of monitoring points on tunnel wall
3 算法验证
在中南大学轨道交通安全教育部重点实验室的动模型试验平台上进行单车试验验证,如图6所示。选择缩尺比为1∶20 的3 车编组CRH380A,即流线型头车+中间车+流线型尾车的组合。变截面隧道总长度为40 m,以模拟总长为800 m的全尺寸隧道,其中中间段的主隧道有效净空面积为70 m2,长为400 m,然后,在两端各设置长为200 m、有效净空面积为100 m2双线隧道。隧道入口为直墙式无缓冲结构,设定车速为300 km/h。在试验前,进行严格的隧道气密性测试,保证隧道段内密封不漏气。

图6 列车通过变截面隧道动模型试验Fig.6 Moving model test of train passing through tunnel with variable cross-section
基于前面所确定的计算条件对试验工况进行模拟,图7所示为动模型试验和数值计算隧道洞壁中部x=400 m 处测点和中间车侧窗测点的压力-时程曲线对比结果。从图7可以看出:在动车组通过变截面隧道过程中,对于车体表面和隧道表面压力变化趋势与其峰值特征,仿真计算结果和动模型试验结果都较吻合,数值计算和动模型试验所得到的压力波动曲线基本重合,压力开始变化和达到峰值的时间基本接近,变化规律一致,压力峰峰值最大相对误差不超过4.2%,从而验证了本数值模拟计算方法的准确性和有效性。
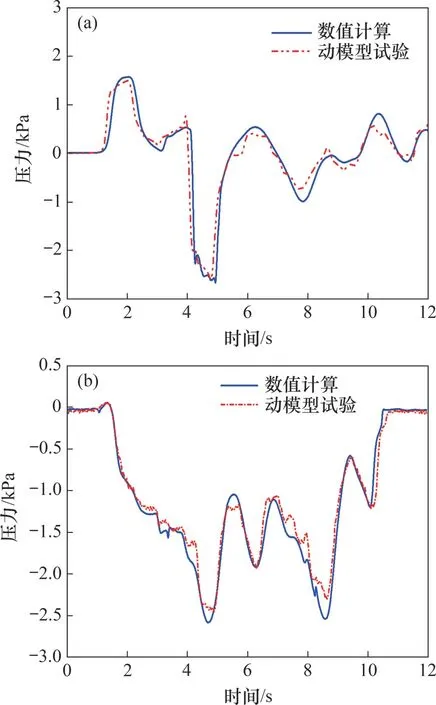
图7 数值计算和动模型试验时程压力对比Fig.7 Comparisons of time-pressure histories between numerical simulation and moving model test
4 结果分析
4.1 隧道洞壁压力
图8所示为变截面隧道、等截面隧道与不同缓冲结构隧道在隧道中部x=400 m(测点6)处初始压缩波形和对应压力梯度变化曲线,表1所示为该测点初始压缩波与压力梯度的峰值。在隧道口增设一定长度的缓冲结构,洞壁初始压力开始上升时间要比等截面隧道和变截面隧道的上升时间早,上升过程也变得更加平缓;初始压缩波峰值并无太大差异,等截面隧道的初始压缩波峰值最大,变截面隧道的初始压缩波峰值最小,设有缓冲结构隧道的初始压缩波峰值则介于二者之间,其中开孔型最大初始压力比不开孔型最大初始压力小13 Pa,变截面隧道的初始压力峰值比断面扩大型、断面扩大开孔型缓冲结构、等截面隧道的初始压力峰值分别小1.6%,2.1%和5.0%。由于列车穿越缓冲结构和变截面隧道,相当于存在二次进洞过程,延长了初始压缩波上升的时间,所以,最大压力梯度比等截面隧道的小,但由于缓冲结构断面积比变截面隧道入口扩大段的断面积大得多,因此,压力梯度也相应较小,变截面隧道最大压力梯度比断面扩大型、断面扩大开孔型缓冲结构分别增大7.3%和21.0%,而比等截面隧道减小25.0%,因此,可以推断缓冲结构对于洞口微气压波的缓解效果要比变截面隧道更好。
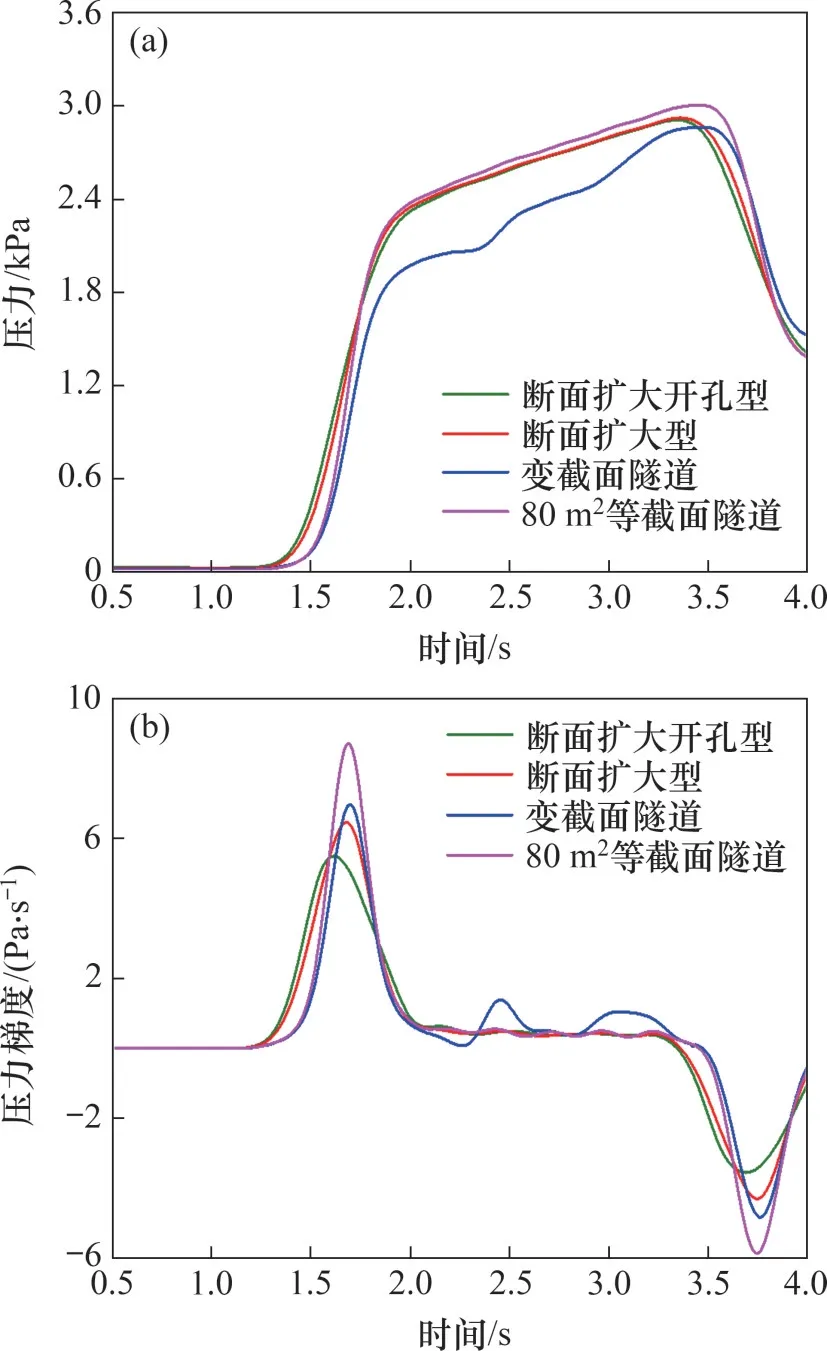
图8 x=400 m处初始压缩波和对应压力梯度Fig.8 Initial compression waves and corresponding pressure gradients at x=400 m
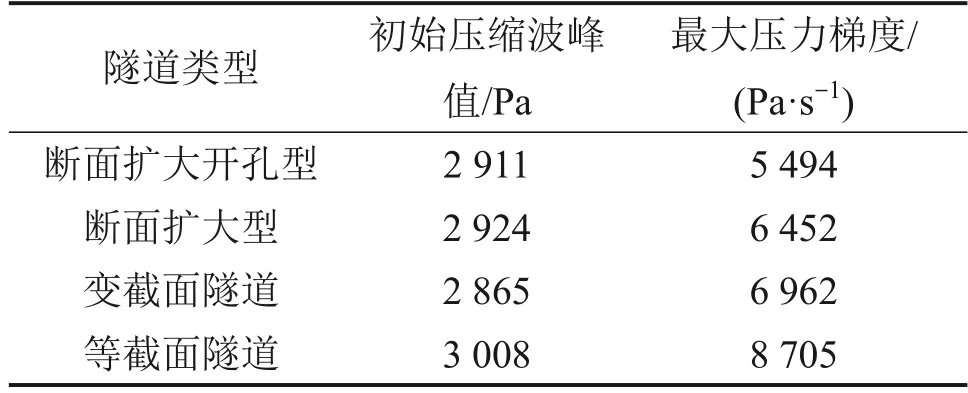
表1 x=400 m处初始压缩波峰值与最大压力梯度Table 1 Peak values of the initial compression waves and the corresponding pressure gradients at x=400 m
图9所示为不同隧道配置下洞壁测点沿隧道长度方向的压力幅值分布。变截面隧道洞壁压力变化幅值整体上比断面扩大型、断面扩大开孔型这2种典型缓冲结构的压力变化幅值小,也比80 m2等截面隧道的压力变化幅值小。设置洞口缓冲结构的主要目的是延长初始压力上升的时间从而缓解隧道洞口微气压波,因此,对于隧道壁面压力的缓解效果有限。与80 m2等截面隧道相比,断面扩大型缓冲结构隧道、断面扩大开孔型缓冲结构隧道、变截面隧道均在一定程度上减缓了隧道洞壁正、负压峰值和压力峰峰值,洞壁x=400 m处测点压力变化峰峰值分别减小152,177 和582 Pa,减幅分别达2.0%,2.3%和7.6%。变截面隧道对隧道洞壁面压力的缓解效果比典型缓冲结构的缓解效果好,增设缓冲结构对于减缓隧道内瞬变压力的效果则不显著。
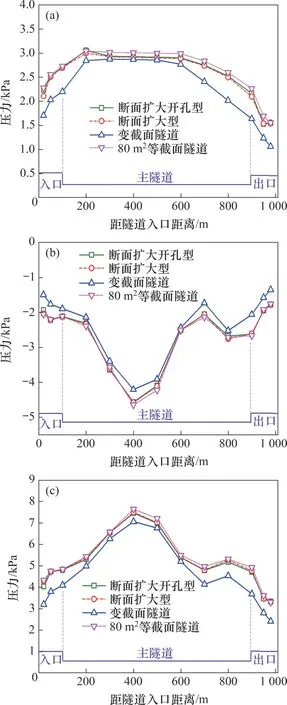
图9 不同隧道配置下隧道洞壁压力变化幅值Fig.9 Pressure amplitude on tunnel surface under different tunnel configurations
4.2 车体表面压力
图10 所示为不同隧道配置下车体表面测点沿车身方向的压力幅值分布。从图10 可见:变截面隧道车体表面压力正峰值、负峰值、峰峰值曲线均比断面扩大型、断面扩大开孔型这2种典型缓冲结构的低,也比80 m2等截面隧道的低,而缓冲结构的开孔对压力变化的影响很小。图11 所示为不同隧道配置下头尾车车体表面测点压力时程曲线。从图11 可见:设有缓冲结构隧道与等截面、变截面隧道相比,在标记1 处车体表面压力上升时间早,因此,压力上升过程较平缓。由于缓冲结构相当于额外延长了隧道长度,车尾进入缓冲结构的时间比车尾进入等截面、变截面隧道的时间早,所产生的初始膨胀波提前向洞内传播,导致标记2处缓冲结构隧道压力提前下降,从而减小了压力正峰值。变截面隧道由于扩大段的作用,从车头进隧道时削弱了初始压缩波和1~3 s 时的摩擦效应强度。与80 m2等截面隧道相比,断面扩大型缓冲结构隧道、断面扩大开孔型缓冲结构隧道和变截面隧道对于头车鼻尖处测点压力峰峰值分别减小177,204 和516 Pa,减幅分别为3.2%,3.7%和9.3%,可见变截面隧道对车体表面压力缓解效果比典型洞口缓冲结构的缓解效果好。
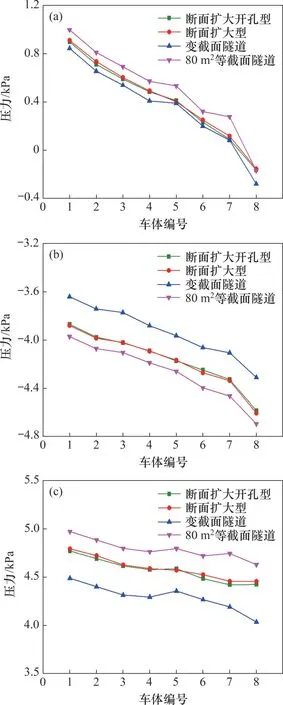
图10 不同隧道配置下车体表面压力变化幅值Fig.10 Pressure amplitude on train surface under different tunnel configurations
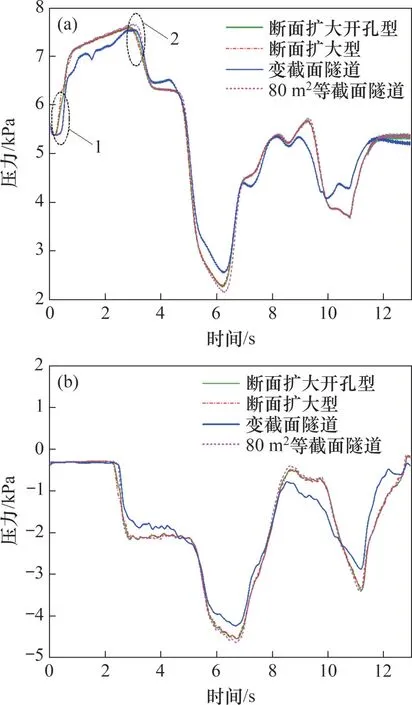
图11 不同隧道配置下车体表面压力时程曲线Fig.11 Time-pressure histories of monitoring points on train surface under different tunnel configurations
4.3 洞口微气压波
高速列车车头突入隧道所形成的初始压缩波以音速向前传播,小部分以脉冲压力波形式在隧道出口向外辐射,并伴有爆鸣声,简称微气压波。该现象将对隧道出口附近环境构成不良影响,亟待防治[27]。据文献[28]可知,不同隧道结构洞口微气压波波峰基本上与方向无关,近似以球状向外辐射,因此,测点布置选取隧道中心线,距离轨面高度为1 m,距离隧道出口分别为20,30,40和50 m。图12 所示为不同隧道配置下洞口微气压波时程曲线,表2所示为不同隧道配置下洞口微气压波峰值随出口距离的变化。从图12 和表2 可以看出:断面扩大型、断面扩大开孔型这2种典型缓冲结构洞口微气压波比变截面隧道的小,因为变截面隧道扩大段的隧道净空断面(100 m2)比典型缓冲结构净空面积(160 m2)小得多,而微气压波主要是流线型车头突入隧道时产生的压力首波造成的。隧道入口处净空断面积越大,初始压缩波压力梯度越小,辐射的微气压波也越小,因此,在变截面隧道扩大段断面有限的情况下,对洞口微气压波的缓解有限,设计变截面隧道的初衷主要是为了缓解隧道内的气动效应,若大幅减缓洞口微气压波,则还需采用洞口缓冲结构或者采用扩大段更大断面的变截面隧道。与相同配置的等截面隧道相比,变截面隧道对于洞口微气压的减缓效果仍较明显,距离出口20 m 处,微气压波峰值最大减小25%。若变截面隧道洞口微气压波峰值不满足要求,则推荐变截面隧道与洞口缓冲结构一起配套使用,这可进一步减小隧道洞口微气压波。
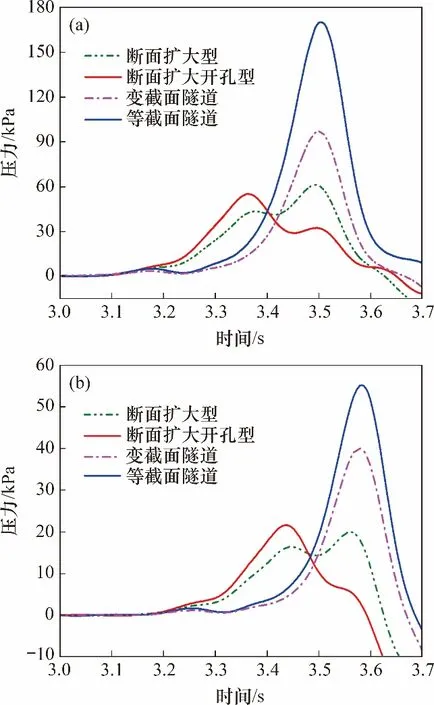
图12 不同隧道配置下洞口微气压波时程曲线Fig.12 Time histories of micro-pressure waves under different tunnel configurations
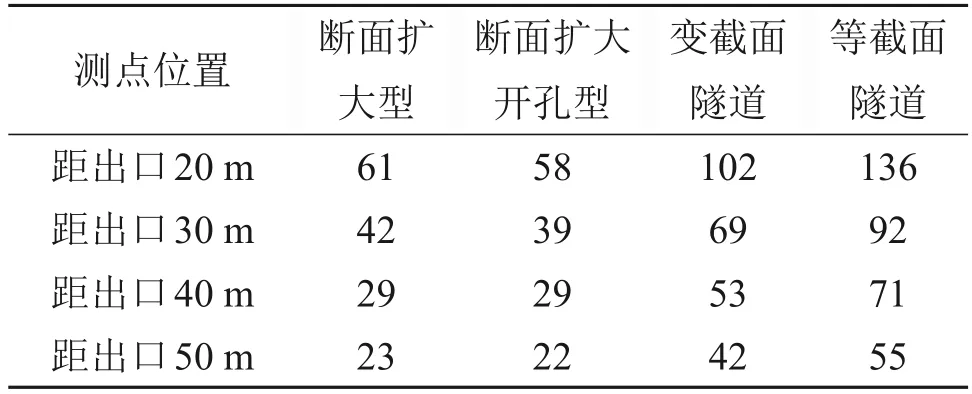
表2 不同隧道配置下洞口微气压波峰值随距离的分布Table 2 Peaks of micro-pressure wave at the tunnel exit under different tunnel configurations Pa
5 结论
1)在相同工况下,变截面隧道动模型试验结果和数值模拟结果较吻合,压力峰峰值最大误差仅为4.2%,验证了数值计算方法的可靠性。
2)变截面隧道与增设缓冲结构的等截面隧道相比,其对车体表面、隧道洞壁压力的缓解效果比典型洞口缓冲结构的缓解效果好,而对微气压波的缓解效果比典型缓冲结构的差。
3)断面扩大型缓冲结构隧道、断面扩大开孔型缓冲结构隧道、变截面隧道与等截面隧道相比,隧道洞壁最大压力峰峰值分别减小2.0%,2.3%和7.6%,车体表面最大压力峰峰值分别减小3.2%,3.7%和9.3%。增设缓冲结构对于减缓洞内压力效果不显著。
4)若变截面隧道洞口微气压波峰值不满足要求,则可推荐变截面隧道与洞口缓冲结构一起配套使用,或者仅采用两端更大断面的变截面隧道,这2种方法均可进一步缓解隧道洞口微气压波。
