地铁隧道壁面压力特性实车试验研究
2022-06-26王凯文熊小慧张洁李小白那艳玲江崇旭
王凯文,熊小慧,张洁,李小白,那艳玲,江崇旭
(1.中南大学交通运输工程学院轨道交通安全教育部重点实验室,湖南长沙,410075;2.中南大学轨道交通安全关键技术国际合作联合实验室,湖南长沙,410075;3.轨道交通列车安全保障技术国家地方联合工程研究中心,湖南长沙,410075;4.中国铁路设计集团有限公司城市轨道交通数字化建设与测评技术国家工程实验室,天津,300308)
随着城市快速轨道交通的普及[1],中国多条地铁线路的最高速度达120 km/h,发展高速地铁线路已成为一种新的趋势。然而,随着列车速度的提高,地铁列车在经过隧道洞口或中间风井等位置时将产生强烈的瞬态压力,直接威胁隧道内维修人员和附属设施结构安全[2-4]。目前,学者主要讨论高速铁路隧道的空气动力学问题[5-7],并通过设置洞口缓冲结构和优化列车头型等方法减缓隧道气动效应[8-9]。与相对顺直且结构简单的高速铁路隧道相比,地铁隧道具有地下段比例高、阻塞比大(地铁隧道阻塞比为0.4~0.6,为高速铁路隧道的3~4 倍)的特点,且隧道沿线通常设置有车站和通风竖井,在2条单线隧道之间还建有防火门的联络通道。独特的地铁隧道结构导致列车穿越地铁隧道引发的空气动力学问题与常规高速列车-隧道耦合空气动力特性有所不同。因此,为使高速地铁系统安全发展,单独研究地铁列车-隧道耦合气动特性十分必要。
近年来,国内外学者对地铁列车通过隧道的瞬态压力开展了研究[10-12]。XIONG 等[13]分析了地铁列车内外的压力波动规律,并研究了隧道洞口、通风井和列车速度对地铁列车空气动力学效应和乘客耳朵舒适度的作用机制;HUANG等[14]对比了不同隧道横截面形状下的隧道壁面压力;冉腾飞等[15-16]分析了不同风井尺寸下地铁列车和隧道壁面的瞬变压力,并获得了速度为140 km/h 的高速地铁隧道净空断面面积与列车密封指数的匹配关系。此外,学者们对地铁隧道内的活塞效应进行了相关研究,发现受限空间比自由空间具有更大的阵风幅值,活塞效应是导致该幅值增大的主要原因[17]。KE等[18]使用地铁环境模拟(SES)软件和计算流体力学(CFD)方法模拟地铁站的环境控制系统,发现活塞效应主要受隧道面积和风井的影响。而通风井同样会影响地铁隧道中列车的空气动力学特性[19-20]。由此可见,现有研究主要采用数值模拟和动模型试验方法,很难复现地铁隧道实际的复杂结构和特殊行车方式。实车试验作为最直接的测试方法,可为地铁隧道压力波理论和数值模拟预测的发展提供数据支撑,但目前相关研究鲜有报道。因此,本文作者采用实车试验方法对地铁隧道内的压力波开展研究,利用马赫图分析压力的传播机理,分析不同风井条件和车速等级下隧道壁面的压力分布规律。研究成果可为地铁列车的运营维护和隧道附属设施的设计提供参考。
1 实车试验方法
1.1 试验概述
实车试验区间全长4.525 km,其中隧道段长2.768 km(车站除外)。列车在2 个相邻车站之间运行,区间包括开放线路、隧道入口和通风井,见图1。隧道净空面积22 m2;风井的横截面长×宽为4 m×4 m,高度为15 m。列车采用6 节编组B 型车,总长为114 m,车宽为2.8 m,车高为3.8 m,横截面积为9.64 m2。列车与隧道断面的阻塞比为0.44。

图1 实车试验区Fig.1 Real train test area
列车自动防护(ATP)是列车自动化驾驶控制系统,目前,GB 50157—2013“地铁设计规范”[21]只适用于速度低于100 km/h 的地铁列车;而试验中地铁列车高速通过隧道区间的压力测试速度为70~95 km/h,因此,选择当前地铁系统的常用运行模式ATP 进行研究,车速分别为70,80,85,90和95 km/h。为研究不同速度等级、风井条件和运行方向对隧道内交变压力的影响,设置了11 组试验,试验的参数设置见表1。图2 所示为车速90 km/h 工况下的列车牵引图。列车在隧道内恒定速度运行,平均速度不确定度小于1%。试验中,列车的加速和制动在隧道外进行,因此,可忽略加减速对隧道内测量结果的影响。

图2 列车牵引图Fig.2 Experimental train traction diagram
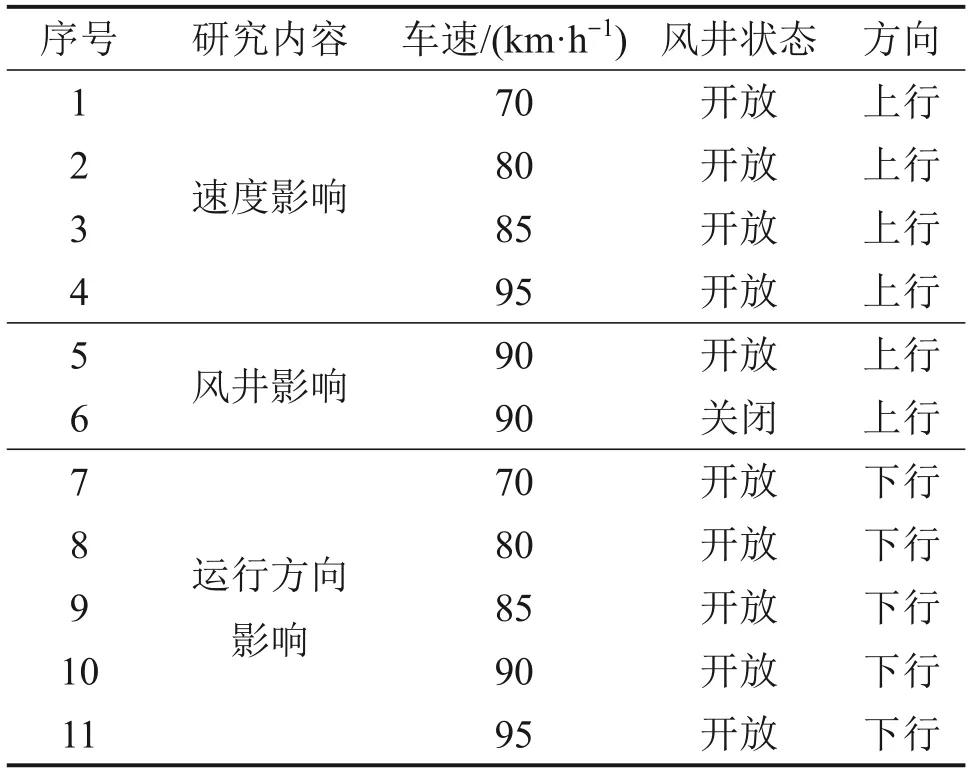
表1 试验的参数设置Table 1 Parameter setting in experiments
1.2 测试系统
试验系统由动态传感器、屏蔽信号线、数据记录系统和计算机处理器组成。数据采集采用多通道IMC设备,见图3。隧道内列车的气动效应呈现非定常、复杂湍流现象,因此,采用Honeywell差压传感器收集压力。霍尼韦尔差压传感器的测量范围为(-2 500,+2 500) Pa,全量程校正在±0.5%范围内。根据EN-14067-5 标准[22],采样频率应至少为Utr/LN的5倍(其中,Utr为车速,LN为列车流线型长度),滤波器截止频率为采样频率的1/4。本试验列车最高速度为95 km/h,车头流线型长度LN约2 m。经计算可知:试验最小采样频率和最小截止频率分别为66 Hz 和16.5 Hz。为保证数据覆盖范围,本试验的采样和截止频率分别选择200 Hz和50 Hz。
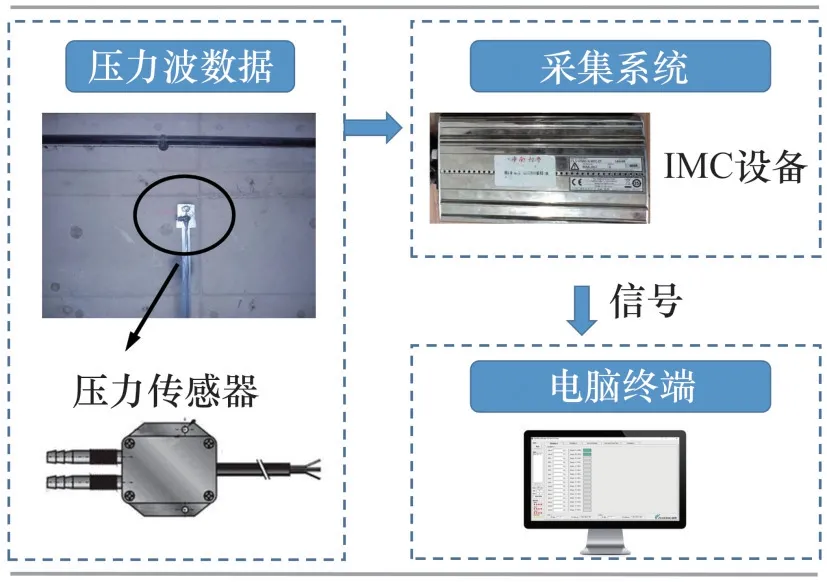
图3 数据采集系统Fig.3 Data acquisition system
1.3 测点布置
压力传感器安装在隧道沿线1.5 m 高的壁面上,在洞口和风井附近的壁面上共布置20 个测点(上下行测点对称),见图4。由于中隔墙门和横通道门的受力面积较大,易受隧道内压力波影响,因此,在距洞口110 m 和490 m 处分别布置测点;当通风井打开时,列车以5种不同的速度通过上行和下行隧道;当风井关闭时,列车以90 km/h的速度运行。

图4 压力测点布置Fig.4 Arrangement of pressure experimental points
1.4 数据处理方法
为便于比较和分析,数据采取量纲一化处理。气动压力采用压力系数Cp表示:

式中,q为动压力;q=ρ为空气密度,ρ=1.225 kg/m3;p为隧道壁面的静压;pref为参考压强。
2 试验方法验证
2.1 重复性分析
为了验证试验系统的可靠性,对车速90 km/h下测点TN-490 的压力系数进行3 次重复试验。试验结果如表2 所示,测点TN-490(距洞口490 m)的压力系数曲线如图5所示,其中,Cp,pp为正压力系数峰值,Cp,pn为负压力系数峰值,ΔCp为压力系数峰峰值;“Entry”垂直线表示列车进入洞口或站台2;“Exit”的垂直线表示列车离开洞口或站台2。从图5 和表2 可知:3 次重复试验测得的压力系数曲线基本一致,压力系数峰峰值的相对标准差为0.44%,因此,可以认为本文的测量方法具有良好的重复性和可靠性。

表2 列车90 km/h驶离隧道时的压力系数峰峰值重复性试验结果Table 2 Repeatability experimental pressure coefficient peaks of train exiting tunnel at 90 km/h
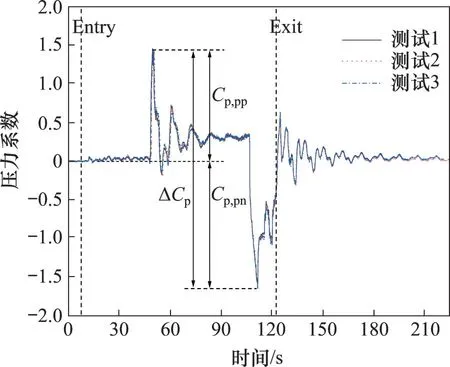
图5 测点TN-490压力系数曲线Fig.5 Pressure coefficient curves of at TN-490 position
2.2 不确定度分析
为了研究列车速度误差、测点布置偏差和环境因素对试验系统误差的影响,采用不确定度作为衡量依据。试验采用压力传感器直接测量隧道压力系数,测量模型为Y=X。
A类不确定度主要反映列车速度偏差、环境变化等因素的影响,可通过n次测量的算术平均值的试验标准差表示:

式中,sA(xˉ)为A 类不确定度评估值;n为试验样本数,本文取n=3;s(x)为标准差。
B类不确定度主要反映试验传感器、信号传输线等因素的影响。假设在区间内样本均匀分布,置信因子为,则传感器引起的不确定性为
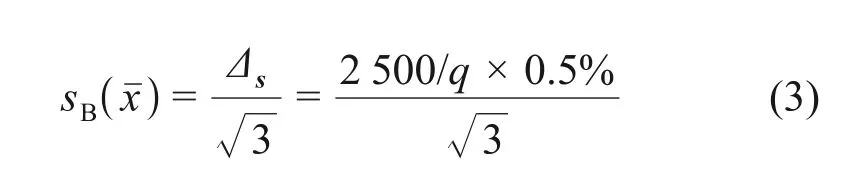
式中,sB(xˉ)为B 类不确定度评估值;Δs为由传感器导致的不确定度。
根据经验,采集器和信号传输线对不确定度的影响可以忽略,且不确定度分量相互之间没有影响,因此,综合不确定度s(xˉ)为
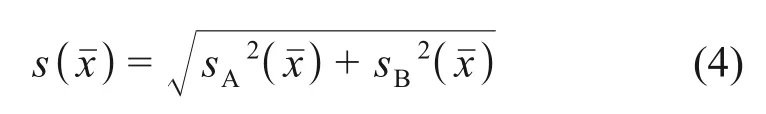
根据式(2)~(4)可得:s(xˉ)=0.020 3,因此,ΔCp=3.085 9±0.020 3。
3 结果与讨论
3.1 隧道内压力分布
地铁列车在隧道内运行速度对应的马赫数小于0.3,但受壁面约束,研究列车周围气流流动时必须考虑可压缩性。
3.1.1 隧道洞口附近不同位置的压力分布
在风井打开的条件下,列车以90 km/h的恒定速度运行,对不同测点的压力系数曲线进行比较分析。3 个测点TN-20,TN-110 和TN-69 分别距离洞口20,110 和690 m,其压力系数曲线如图6 所示。由于初始压缩波经历最小的能量耗散和受空气黏度作用,所有测点的压力系数均在初始压缩波处获得最大值。同时,测点TN-20的压力波动最小,测点TN-690 的波动最为显著。由于列车头部和尾部进入隧道和车体到达测点的时间并不同步,而测点TN-20主要受列车驶入隧道时的短时间扰动作用,因此,其初始压力上升较低,且存在波形抵消作用。

图6 不同位置的压力系数曲线Fig.6 Pressure coefficient curves of different positions
地铁隧道在纵向上的结构并不对称,使得列车进出隧道产生的气动效应不相同。列车以90 km/h运行时,沿隧道方向的压力系数峰值如图7 所示。从图7可知:列车进出隧道过程的最大压力系数峰峰值分别为4.55和4.01,前者比后者大13.5%。列车出隧道时,隧道洞口测点的波系经历更大的壁面摩擦,因此,压力波动相对较小。此外,在距离洞口110 m 范围内,压力系数幅值变化率较大,之后该变化率减小。由于压力波动与压力传播和列车通过扰动相关,而列车的长度为114 m,因此,在110 m之内,测点离洞口越近,压力系数幅值变化率越大;其他范围测点主要受波系传播影响,其幅值变化率降低。
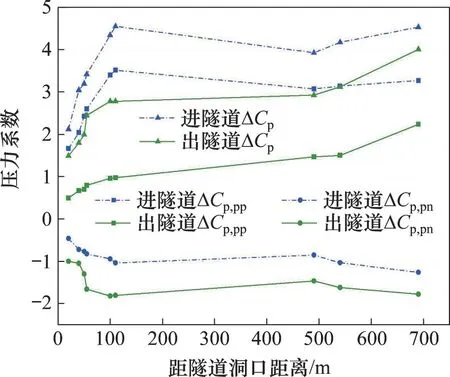
图7 列车90 km/h运行时沿隧道方向的压力系数峰值Fig.7 Peaks of pressure coefficient along tunnel during a train operating at 90 km/h
为了解释上述现象并揭示压力的传播机理,对测点TN-690 进隧道过程的马赫图进行分析。测点TN-690 马赫图和压力系数曲线如图8 所示。从图8可以看出:当车头和车尾进入隧道时,会产生一系列压缩波和膨胀波并以声速传播;当列车进入隧道时,车头进入隧道洞口产生的压缩波传播到测点(①点),压力开始上升。随后,车尾进入隧道引起的初始膨胀波到达测点(②点),导致较大压降。由于初始压缩波和膨胀波传播到风井并被反射至测点,使得压力呈现先上升后下降趋势(③点和④点)。而点⑤和点⑥则对应车头和车尾到达测点的时刻。虽然压力继续传播到测点位置,但多次反射后能量降低,可见随后压力波动较小。从上述分析可知:在列车到达风井之前,初始压缩波和膨胀波在风井处存在反射现象,且该波系随后在风井与入口之间不断传播,马赫图极好地吻合了压力系数曲线的变化趋势。而当列车在73 s经过风井时,由于风井与隧道的面积比为0.7,高速通过风井的列车相当于重新进入隧道,因此,产生另一系列压力波(⑦点),之后的压力波动逐步减小,并趋向于0。⑦点处产生的波系恰好验证了地铁隧道结构的特殊性,在后述的分析中,开放风井还极大地影响了风井区域的波形和传播方式。因此,探讨地铁隧道风井的作用对厘清其隧道内压力分布规律有着重要作用。

图8 测点TN-690的马赫图和压力系数曲线Fig.8 Mach diagram and pressure coefficient curve of TN-690 position
LIU[23]的研究中高速铁路隧道的常见压力波形如图9 所示。将上述TN-690 测点的压力系数曲线与图9对比可以看出:高速隧道的压力波形相对平滑且衰减较慢,其波形主要受初始压缩波和膨胀波的叠加作用;而地铁隧道内由于车站、风井和联络通道等而具有独特的内环境,导致隧道壁面压力衰减更快且压力的叠加更为复杂,需要强调的是地铁隧道的复杂波形并非传感器误差和滤波所致。可见:地铁隧道壁面的压力形成和叠加过程与传统高铁隧道的不同,因此,有必要讨论地铁隧道的独特结构(如风井等)对其空气动力特性的影响。

图9 高速铁路隧道典型压力波形(LIU等[23]图5)Fig.9 Typical pressure waveform in high speed railway tunnel(Fig.5 of LIU et al[23])
3.1.2 风井附近沿隧道长度方向压力分布
不同风井条件下风井区域的压力系数峰峰值如图10所示。从图10可以看出:风井无论处于打开或关闭状态下,其附近隧道壁面测点的压力系数变化幅值均是先减小再增大,在中间风井位置达到最小。开放风井有利于降低风井位置测点的压力系数变化幅值,但同时也会引起风井两侧测点压力系数变化幅值增大。风井的存在使隧道内压力波动更加复杂,并非完全有利于降低隧道壁面压力。列车驶入隧道时,风井右侧25~50 m的隧道壁面产生了增压效果;列车驶出隧道时,增大了风井左侧25~50 m隧道壁面的压力波动。
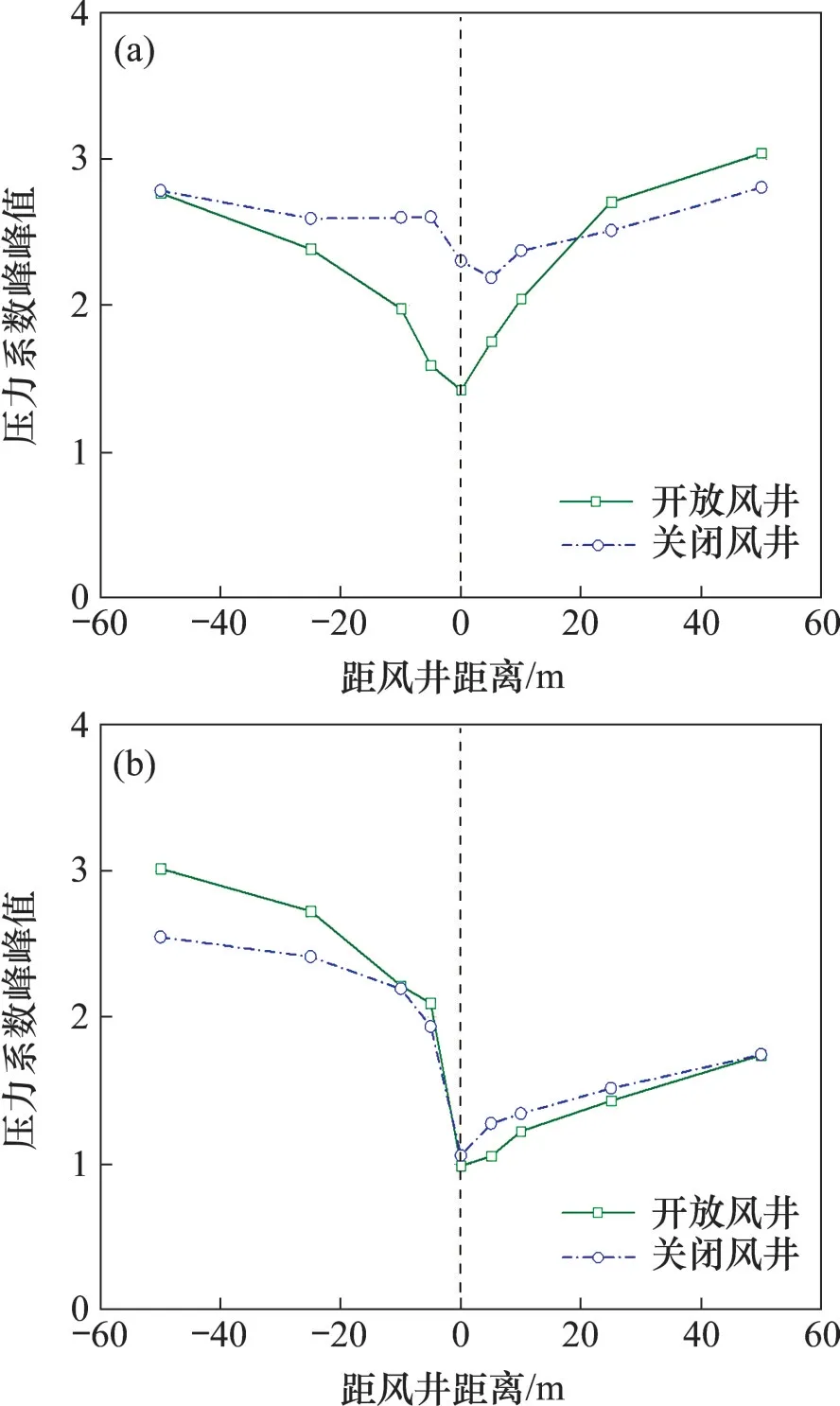
图10 不同风井条件下风井区域的压力系数峰峰值Fig.10 Peak values of pressure coefficient in airshaft area under different airshaft conditions
列车90 km/h运行时风井区域的压力系数幅值如图11 所示。从图11 可以看出:风井位置处隧道壁面的压力波动最小,测点越靠近风井,则泄压效果越明显,且泄压对正压幅值有更好的效果。同时,不同运行方向测点在风井区域的压力分布具有良好的一致性。
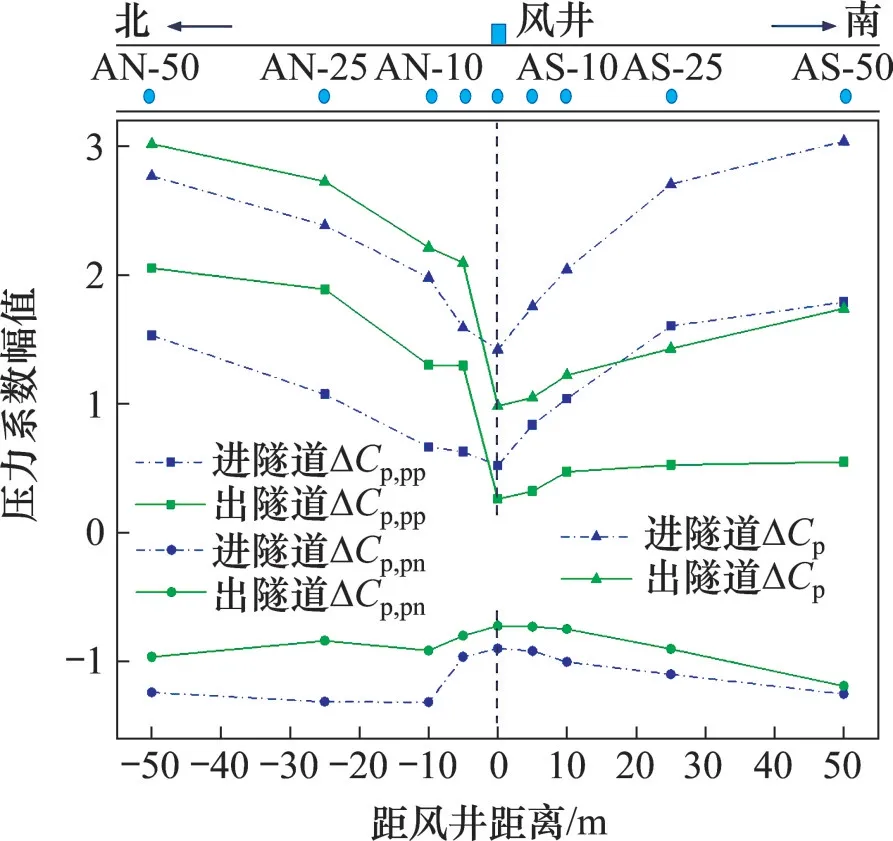
图11 列车90 km/h运行时风井区域的压力系数幅值Fig.11 Pressure coefficient peaks near airshaft during a train operating at 90 km/h
图12 所示为开放风井附近不同位置的压力系数曲线。从图12(a)可以看到:相较于洞口附近的测点,风井可以显著抑制初始压缩波所产生的压力上升幅度(如区域A所示),进而测点的压力系数变化幅值总是在中间风井位置达到最小。而当列车到达风井时,列车头部周围的流场代表负压,因此,风井左侧区域的压力呈现先降低后上升的趋势(如区域B所示),该过程使得风井左侧的大部分空气流向隧道外部,有利于通风和减压。同时,列车通过风井也导致波系更复杂[24],可在风井右侧测点AS-5(距风井5 m的南侧测点)的区域B中观察到。该波系与列车重新进入另一隧道引起的流场相似,使得风井右侧区域的波形与左侧区域的不同,由图12可见:测点AS-5的第二个峰值比初始峰值增大了91%。开放风井对于列车前进方向一侧距风井25~50 m 的隧道壁面反而产生增压效果。隧道壁面的增压区域相对较小,因此,在高速列车运营条件下,通风风井依然有利于隧道内的泄压通风,建议风井设置为开放状态。
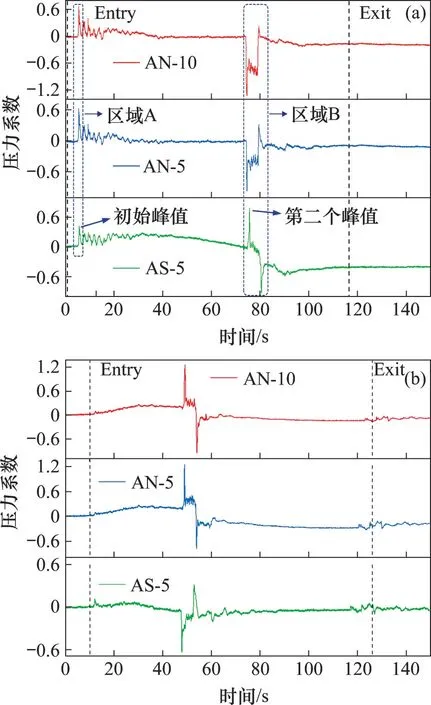
图12 风井区域不同测点的压力系数曲线Fig.12 Pressure coefficient curves of different measuring points near airshaft
3.2 风井条件对风井区域波形的影响
风井条件对其附近测点的波系形态及其传播方式造成影响,以车速90 km/h进隧道为例,不同风井条件下测点的压力系数曲线如图13 所示。从图13 可知:对风井区域测点而言,开放风井抑制了风井区域的初始压力上升幅度和循环周期,且在一定程度上降低了初始压力衰减。

图13 测点AN-5和AS-5的压力系数曲线Fig.13 Pressure coefficient curves of AN-5 and AS-5
风井与隧道联结处压力波传播示意图如图14所示。从图14 可知:当初始压缩波Pi传播到隧道和竖井的联结处时,压缩波小部分以膨胀波Pz的形式反射,另一部分被分成2 个压缩波Pi1和Pi2,Pi1沿风井向上传播,Pi2沿着隧道方向传播。由于风井的导流作用,初始压缩波经历了较大的能量损失和周期性变化,导致初始压缩波的振幅大幅减小;而风井的存在同样改变了测点的压力传播方式,导致初始压缩波的循环周期大幅缩短。初始压缩波压力系数正峰值及相应的循环周期如表3所示。从表3可知:与关闭风井相比,开放风井在测点AN-5(距风井5 m的北侧测点)处的初始压力正峰值降低了78.5%,初始压力循环周期降低了83.4%。
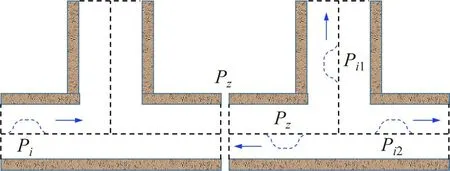
图14 风井与隧道联结处压力波传播示意图Fig.14 Schematic diagram of pressure wave propagation at junction of airshaft and tunnel
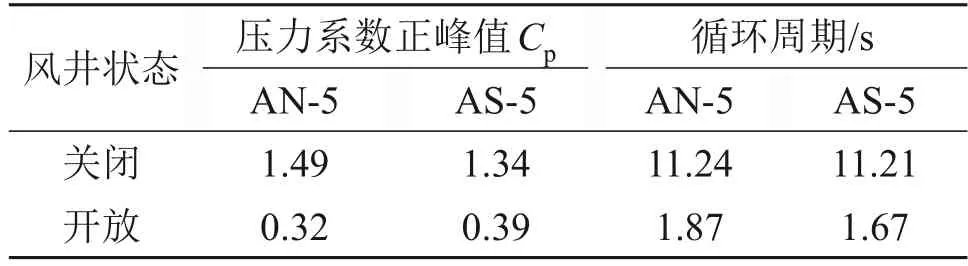
表3 初始压缩波压力系数正峰值及相应的循环周期Table 3 Initial pressure peaks and corresponding cycle periock
3.3 速度的影响
图15 所示为列车以不同速度行驶时沿隧道方向的压力系数峰峰值分布。压力波动主要由初始压缩波和膨胀波的反射和传播引起,因此,随着车速增加,反射波的强度也随之增加,列车运行引起的压力波动在较高速度下更加显著,尤其是车速为95 km/h时。同时,同一测点在不同速度下的气动压力系数差异较小,最大差异约为0.46。
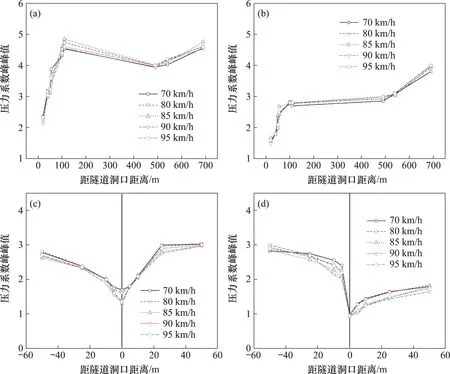
图15 不同车速下隧道内压力系数分布Fig.15 Pressure coefficient distribution in tunnel under different train speeds
不同车速下压力峰峰值的拟合曲线见图16。从图16 可知:最大压力峰峰值与列车速度的平方近似成正比。对于净空断面积22 m2的单线地铁隧道,当列车以95 km/h运行时,作用于隧道衬砌及附属设施的最大压力峰峰值为2.01 kPa。可直接利用拟合公式求得不同速度等级下地铁列车通过隧道时壁面的压力峰峰值。
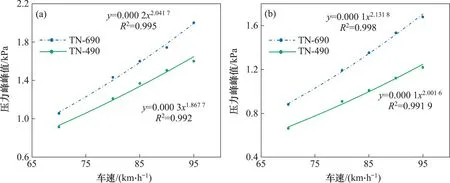
图16 不同车速下压力峰峰值的拟合曲线Fig.16 Fitting curves of peak-to-peak values at different train speeds
为验证上述压缩效应并评估压力,将试验测得的最大初始压缩波与HARA[25]和HUANG等[14]的计算结果进行比较。HUANG等[14]使用数值模拟方法获得了车速80 km/h 时的初始压缩波压力最大值。HARA[25]基于线形声学理论,提出初始压缩波压力最大值的计算公式:
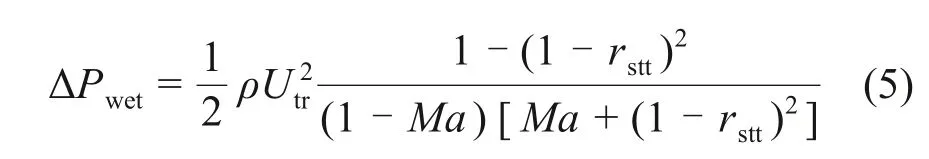
式中,ΔPwet为初始压缩波的最大值;Ma为马赫数,Ma=Utr/c,声速c=340 m/s;rstt为阻塞率,rstt=0.44。
初始压缩波压力最大值测试值与计算值[14,25]对比如图17所示。由图17可知:压力试验值曲线与计算曲线的趋势表现出良好的一致性。但是,与80 km/h 时的计算值[14]相比,进隧道的初始压缩波压力最大值增加了82.9%。其原因如下:在相同速度和阻塞率下,列车具有理想的外形和流线型头部设计,而最大初始压缩波压力随着流线型长度的减小而增大,测试地铁列车头部为钝头结构,流线长度较短,导致空气动力性能较差。

图17 初始压缩波压力最大值对比Fig.17 The maximum pressure of initial compression wave
为了使经验公式适用于该类型地铁隧道,定义气动外形修正系数k对其进行修正。k主要与列车流线长度和头部形状有关,修正公式如下:
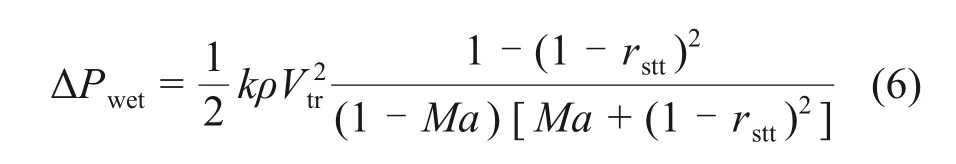
根据试验数据,气动外形修正系数k为1.80~1.85。
由于数值模拟具有较高的阻塞率并采用不同车型,与车速80 km/h时的计算结果相比,进隧道的初始压缩波最大压力降低了7.5%。因此,随着高速地铁的快速发展,地铁外形设计应被视作提高隧道气动性能的重要因素。
4 结论
1)隧道洞口和风井附近的压力变化幅值受列车运行方向的影响,列车进出隧道引起的测点最大压力系数峰峰值分别为4.55 和4.01。当列车以95 km/h 运行时,作用于隧道衬砌及附属设施的最大压力峰峰值为2.01 kPa。
2)与封闭风井相比,开放风井可减少风井位置处的压力变化,显著降低风井区域的初始压缩波压力系数正峰值和循环周期,测点AN-5(距风井5 m 的北侧测点)的初始压缩波压力系数正峰值和循环周期分别降低了78.5%和83.4%;但对于列车前进方向一侧,距风井25~50 m的隧道壁面反而产生增压效果;由于隧道壁面的增压区域相对较小,综合考虑风井的通风和泄压功能,建议风井设置为开放状态。
3)压力系数峰峰值与列车速度的平方成正比。与车速80 km/h时计算的理论值相比,列车进隧道的初始压缩波压力最大值增加了82.9%,需定义气动外形系数k来修正经验公式(k为1.80~1.85)。随着高速地铁的快速发展,地铁外形设计应被视作提高隧道气动性能的重要因素。
