基于热-流-固耦合分析的T型管道数值模拟

潘丽艳，叶 飞，万法林，蔡可文，丁晓培，赵骁冉，张经纬

（江苏东港能源投资有限公司，江苏 连云港 222000）

1 T型管道简介

在核工业、化工业及航天等领域中，T型管道在工作过程中经历冷热流体交混周期变化，引起反复自由膨胀或收缩受到约束而产生循环热应力或循环热应变[1-4]。随着温度的升高，金属材料的强度降低而变形增加[5]。过大的热应力和热应变及流体温度波动导致管道内部晶体错位、微观裂纹扩展，最终导致管道失效[6]，因此T型管道热应力研究受到越来越多的重视。

SELⅤAM等[7-8]利用大涡模拟针对T型管道冷热流体交混现象进行研究，认为浮力效应及低雷诺数流体是导致T型管下游区流体产生热分层的主要原因。BRAILLARD等[9]为了获取T型管道内冷热流体交混导致的流体温度波动设计了新的实验装置，针对主/支管接头部分分别设置为圆角和尖角2种情况分析T型管道下游区温度特性。HANNINK等[10-11]应用流-固耦合分析方法研究流体与结构变形之间的相互作用。XU等[12]采用流-热-固耦合方法分析“L”型管道的热应力，计算了不同工况下管道的等效应力，指出应力分布受温度和压力载荷的共同影响。

综上所述，国内外对T型冷热流体交混管道的相关研究主要集中在管道下游区部分，对上游区管道温度分布、热应力分布及流体速度分布研究鲜有涉及。而该位置同样受热应力影响，有形变发生。此外，管道结构压力受流体压力、温度共同作用，因此分析管道所受热应力的过程必须充分考虑热-流-固（温度、流体、固体管道）三者之间的耦合作用，提高仿真研究的准确性与适用性。

针对以上问题，本文以T型管道内冷热流体交混过程中上游区管壁及流体为研究对象，综合考虑温度载荷及压力载荷对管道热应力的影响，结合热-流-固耦合模型开展稳态计算。研究结果可为T型管道内冷热流体交混初期接口处上游区的安全裕度及结构设计提供依据。

2 数学模型

2.1 流体理论

本文中数值模拟采用标准的k-ε模型计算流体流动和传热情况。标准的k-ε模型以N-S方程为湍流运动基本方程，在紊流动能k（J）方程的基础上，引入紊流耗散率ε（%）方程。结合质量方程、动量方程和能量方程得到k-ε模型。

质量守恒方程为：

式（1）中：ρ为流体密度，kg/m3；ui为流体流速，m/s。

动量守恒方程为：

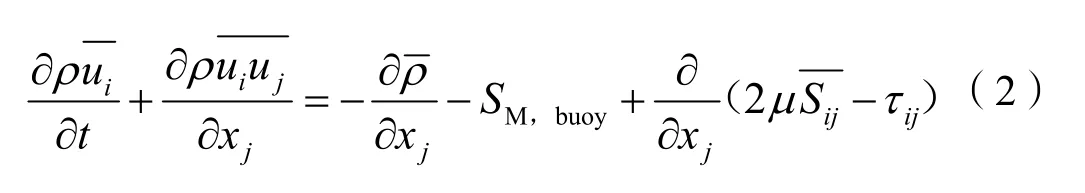
式（2）中：SM，buoy为浮力，N；为应变张量；τij为雷诺应力，N。

能量守恒方程为：

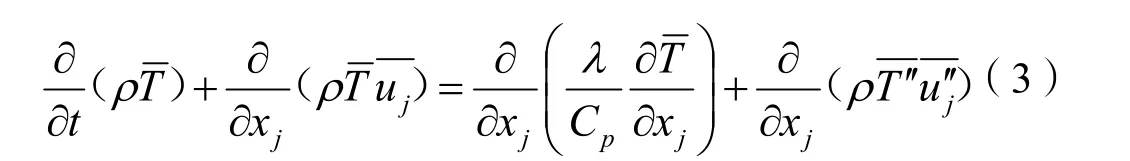
N-S方程在直角坐标中写成：

式（4）中：p为压力，N；X、Y、Z为外力的分量，N；μ为动态粘度，N·s/m2；Δ为拉普拉斯算子；u、v、w为流体在t时刻，在点（x，y，z）处的速度分量，m/s。

由于平均N-S方程的不封闭性，引入二方程湍流模型来封闭方程组，紊流动能k方程为：

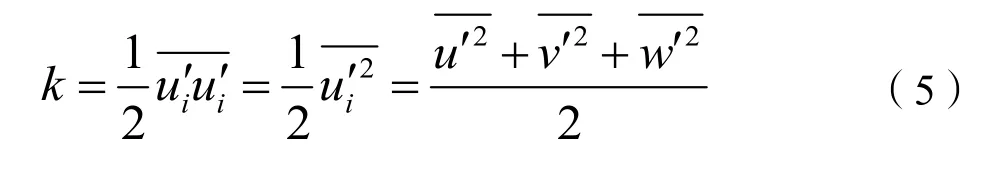
在k方程基础上引入紊流耗散率ε方程：

式（6）中：μe为湍流粘性系数，Pa·s；c1、c2为经验系数；Gk为剪切应力，N；k为紊流动能，J。

综合质量方程、动量方程和能量方程，得到含k-ε模型的紊流流动基本方程：

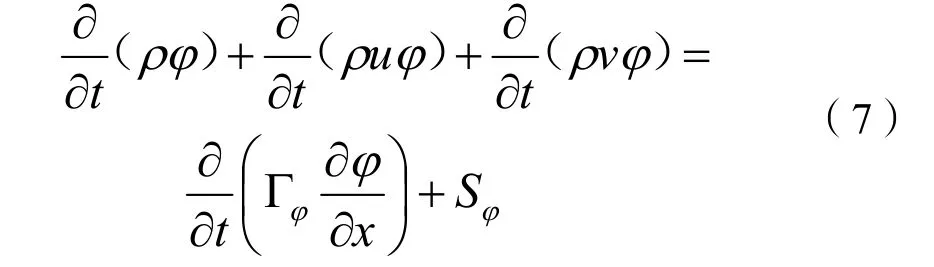
式（7）中：u、v为x、y方向动量，kg·（m·s-1）；φ为耗散率，%；Sφ为耗散项，J。

2.2 固体模型

通常，在固体分析中需满足以下假设[12]：K矩阵必须是连续的，相应的材料具备各向同性、均匀性，变形时应满足胡克定律。F矩阵为静态载荷，不考虑负载和惯性随时间变化的影响。基于经典力学原理，建立整体结构的运动方程为：

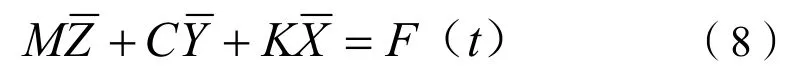
式（8）中：M为质量矩阵；为加速度矢量；C为阻尼矩阵；为速度矢量；K为刚度系数矩阵；为位移矢量；F为受力（自身的重力、流场压力等），N。

力学平衡方程为：

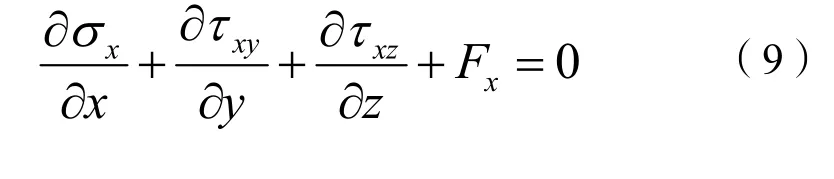
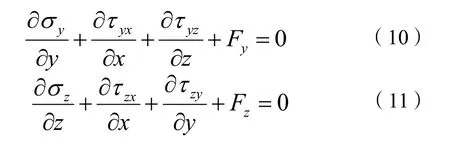
式（9）—（11）中：σi为法向应力（i=x，y，z），N；τj为剪切应力（j=xy，yz，zx），N；Fk为体积力（k=x，y，z），N。

3 数值模拟

仿真分析与实验数据分析对比如下。

利用冷、热流体间温差（ΔT=Th-Tc）将流体温度标准化，瞬时温度（T）标准化方程为：

归一化平均温度为：

式（13）中：N为数据采样点的数量。

通过在管道不同截面（5d、5.5d，d为管道直径），设置A（θ=324.5°）、B（θ=279.5°）、C（θ=234.5°）、D（θ=189.5°）4个监测点，求解各监测点的归一化平均温度，该结果与实验结果进行对比。监测点位置对应的管道位置如图1所示。如图2和图3所示，将本文算例中应用标准的k-ε模型计算得到横截面的归一化平均温度（）与斯图加特大学材料测试研究所实验数据（）[13]相比较，靠近管道下部区域（θ=189.5°）的值接近1，说明冷热流体交混现象越充分，温度波动越大。靠近管道上部区域（θ=324.5°）的值最低，说明该区域热混合很少。本文数值模拟后得到的归一化平均温度与测量数据相比，平均误差为4.15%，相比以大涡模拟为计算模型的数值模拟产生的平均误差减小约12.63%[7]。其中，本文中误差最小值达到1.46%，与实验数据非常吻合。

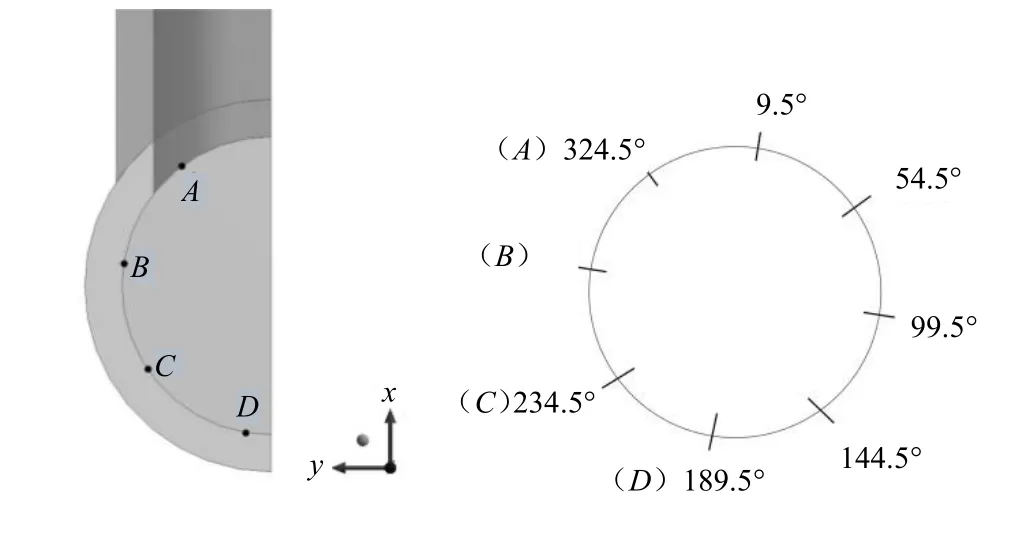
图1 对比点位置

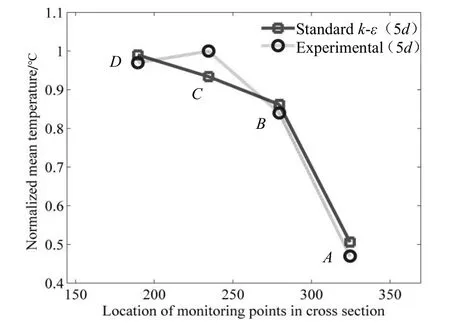
图2 5d处实验数据对比分析

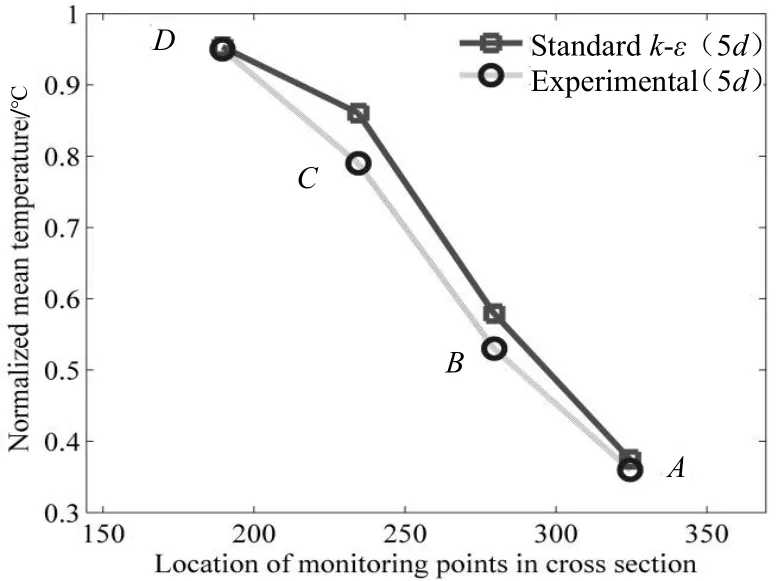
图3 5.5d处实验数据对比分析

图4给出在压力负载、温度负载和耦合负载分别作用下管壁受到的最大等效应力。图4中，不考虑温度负载的流-固耦合分析得到的热应力非常小。而增加温度负载后，热-固分析与热-流-固分析后得到的热应力相差很小，但随着流体压力的增加，二者之差越来越大。

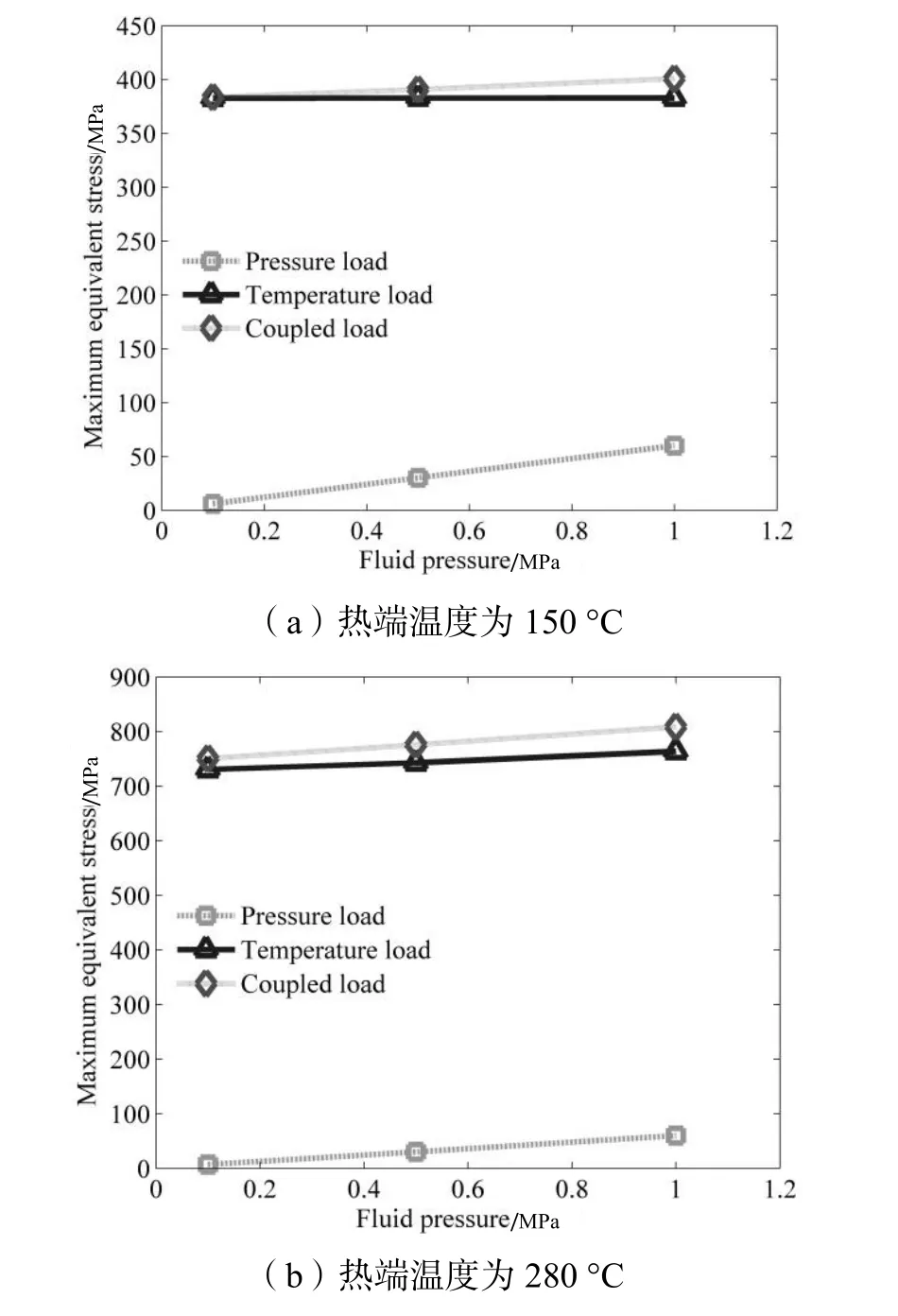
图4 不同负载类型作用下最大等效应力

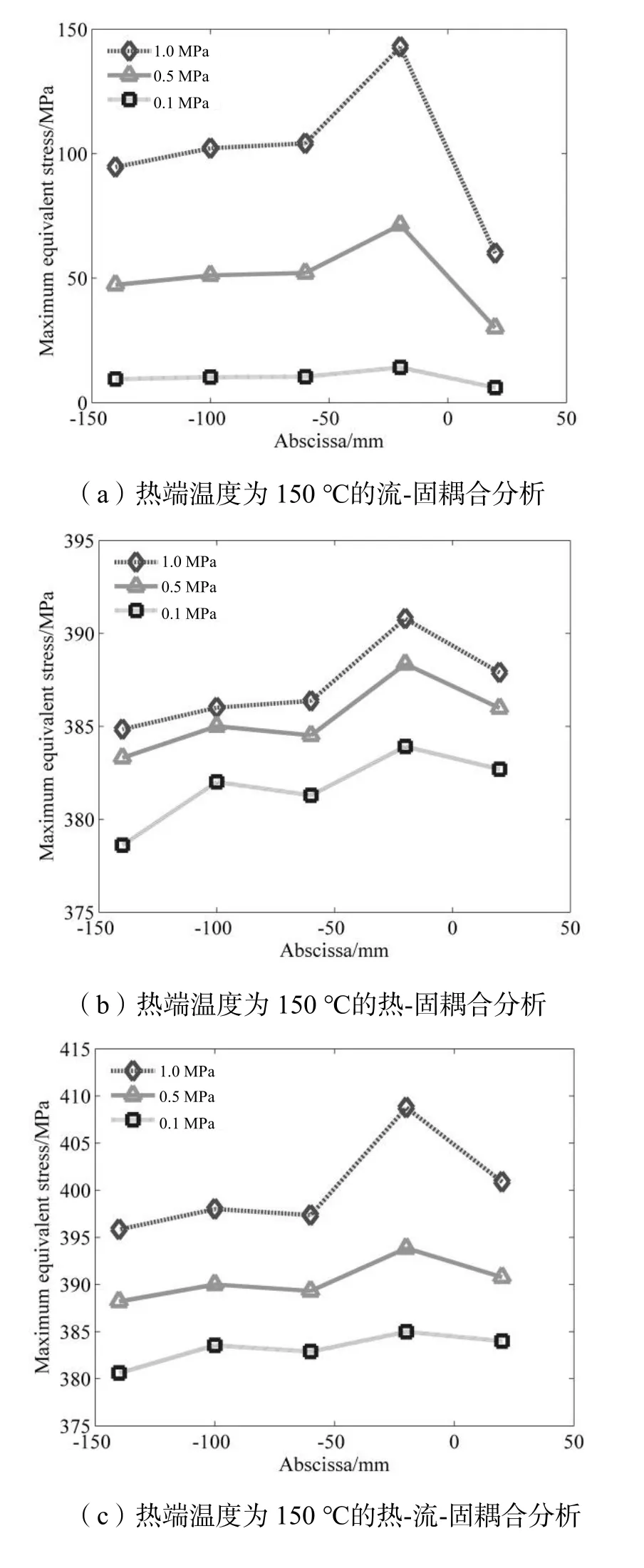
图5显示了热流体温度为150℃和280℃时管道上部不同监测点对应的最大等效应力。流-固耦合分析中流体温度从150℃增加到280℃，最大等效应力增量小于5%；对于热-固和热-流-固分析，最大等效应力增量达到192.5%和198%。因此在计算T型管道热应力时必须加入热分析模块，单纯应用流-固耦合分析得到的结果是偏离实际情况的。

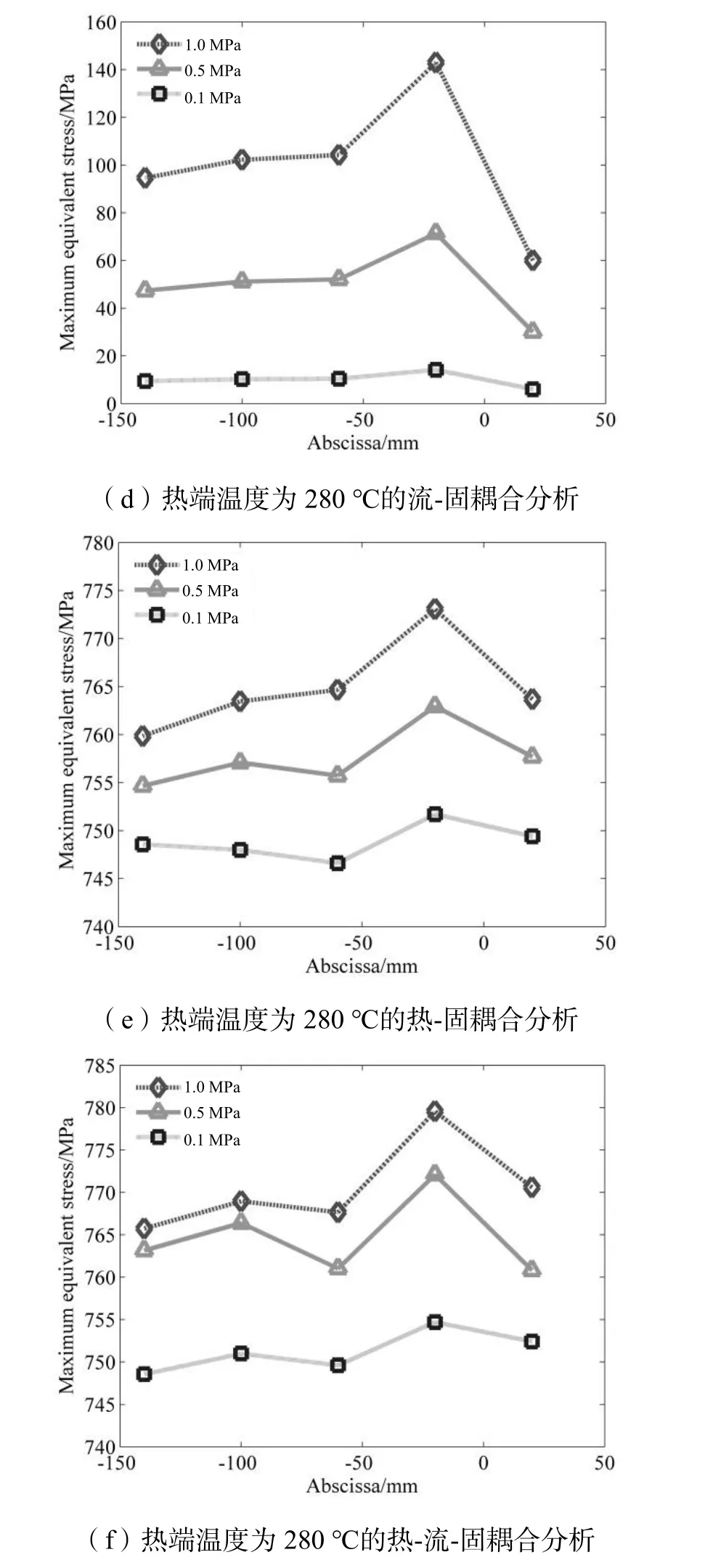
图5 不同负载作用和位置的管道最大等效应力分析

复合载荷作用下的应力不等于压力和温度载荷之和，对于管道应力，温度载荷的影响远远超过应力载荷的影响。温度越高，耦合作用越大，因此在分析管道所受应力时，不能忽视压力与温度之间的耦合作用。

耦合作用和非耦合作用下产生最大等效应力存在很大差异，通过比较两者之间的应力差来探索耦合作用的影响，复合载荷与非复合载荷作用下的最大等效应力差如图6所示。当流体温度在160～280℃之间，管道接口上游区在低压区（0.1 MPa）最大等效应力差值在2.3～8.8 MPa范围内，相对很小。

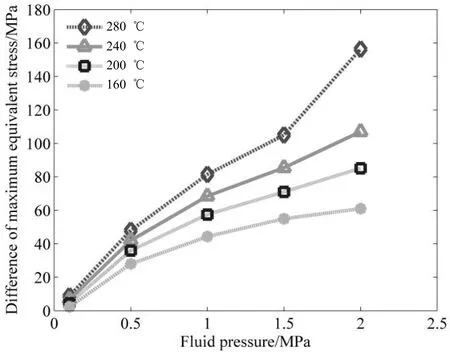
图6 耦合及非耦合作用下管道最大等效应力差

随着热端流体温度和压力的升高，差值逐渐增大，在高压区（2.0 MPa）达到61～156.3 MPa。由此可见，耦合作用随着温度和压力的增加而成非线性比例增加，并且最大等效应力差呈发散趋势，因此在计算T型管道热应力时必须考虑流体温度和压力的耦合作用对热应力的影响。

4 总结

本文利用热-流-固数学模型分析了冷热流体交混管道接口处上游区的速度场与温度场，综合考虑温度场和流场获得了不同工况条件下的热应力场，着重研究了耦合作用对管壁最大等效应力的影响。结果表明：①流-固分析中流体温度从150℃增加到280℃，最大等效应力增量小于5%；对于热-固和热-流-固分析，最大等效应力增量达到192.5%和198%。压力载荷和温度载荷同时作用于管道，最大等效应力主要受温度负载的影响，随着温度的升高，耦合效应变大。②耦合作用下产生的最大等效应力与各负载单独作用产生的应力之和呈非线性关系。因此，工程中计算管道热应力必须考虑压力与温度之间的耦合作用。