基于单幅图片的有效信息提取＊

王朋豪，张鹏程，杨滟涛，谢婷婷，杨祖恒，陈美松

（西南石油大学理学院，四川 成都 610500）

近10年来，随着相机的普及，视频图像分析不断发展。特别是在当前热门的移动机器人、无人驾驶、计算机视觉和无人机侦察等领域，应用需求较大。在设计未来智能交通系统时，科研人员使用双目视觉系统、多目视觉系统、特殊配置的单目视觉系统获取相关信息，但在某些特定条件下，分析人员所能利用的只有普通的图像或视频，其中的信息需要综合考虑各种影响因素，并利用适当的数学模型来提取。本文选择视频的关键帧——“单幅图像”作为研究对象，对单幅图片进行分析研究，提取视频中关键目标的大小、距离和速度等信息，具有很强的现实应用价值。

近些年，单幅图像建模的研究越来越受到人们的关注。由于单幅图像无法完全重构出对应的三维模型，众多研究者利用图像中已知的几何信息对目标物体进行三维重建从而得到想要获取的关键信息[2]。在国外，CAPRILE和TORRE首先提出利用灭点进行摄像机标定的思想[3]，在证明了灭点属性的基础上，根据灭点与摄像机内参数的关系，由单幅图像确定摄像机的内参数；同时结合特定模板计算摄像机的外参数；GUILLOU等提出了一种利用灭点实现单幅图像中三维物体重建的方法等将目标物体的几何形状作为相应参数，实现结构化场景的交互式建模[4]。在国内，对利用单幅图像进行建模工作的研究也很多，张祖勋通过分析灭点几何建立了影响直线段与方位元素的直接联系，根据最小乘二平差的有关理论给出迭代计算影像的内外方位元素的方法[3]。

本文将利用一种未定标相机构造三维模型的方法，该方法利用3个灭点确定相机的内部参数矩阵，通过分解基础矩阵求解出相机的外部参数，从而完成相机的定标过程，在此基础上，实现图片信息提取，且本方法更易操作实现。

1 坐标系介绍

常用的坐标系有像素坐标系、图像坐标系、相机坐标系和世界坐标系。

1.1 像素坐标系

像素坐标系用（u，O，v）表示，O为坐标原点，位于图象左上角。u，v分别表示横纵坐标轴并相互垂直，u与水平方向平行，v与水平方向垂直。该坐标系可以表示以像素为单位的图像，如图1所示。

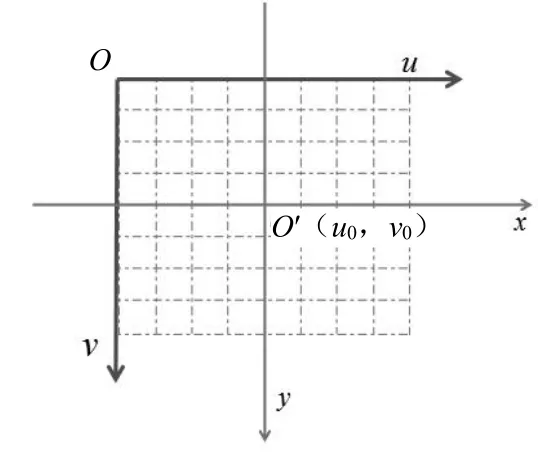
图1 像素坐标系

1.2 图像坐标系

像素坐标系中的坐标只表示存储位置，无法表示像素的物理位置。为了有效表示像素点在成像平面上的物理位置建立图像坐标系。将该坐标表示为坐标原点为光心在像平面的投影。图像中心的像素坐标是（u0，v0），dx，dy分别为物理尺寸及单个像素的宽和高，图像坐标系的坐标（x，y）与像素坐标系的坐标（u，v）之间的关系可以表示为：

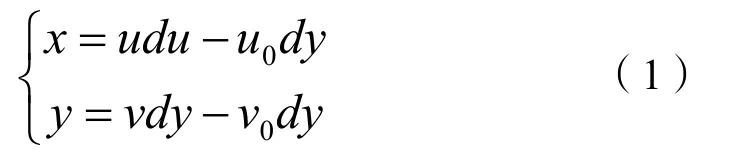
则：

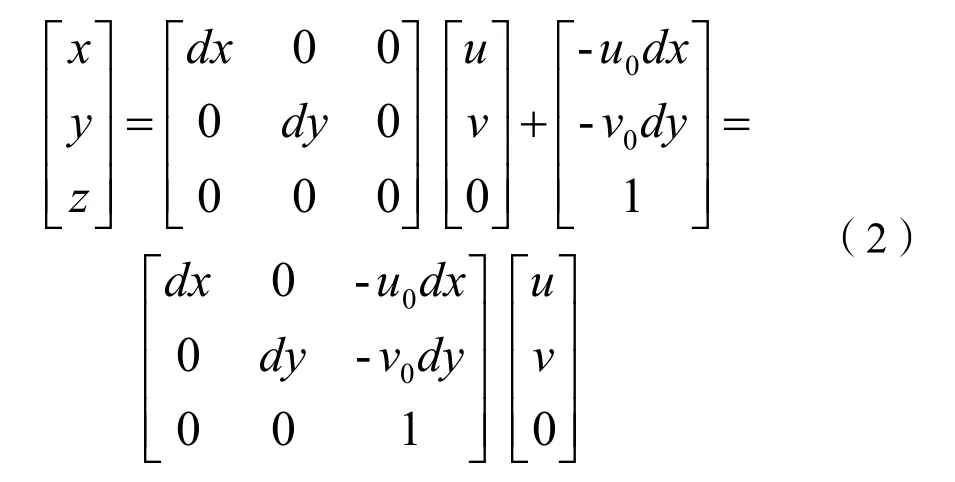
1.3 相机坐标系

图像坐标系、相机坐标系和世界坐标系的关系为：相机坐标系表示为（Xc，Yc，Zc），以光心为原点，Xc、Yc分别与图像坐标系的x轴、y轴平行，Zc轴和相机的光轴重合并垂直于成像平面。光心和与成像平面间的物理距离即为成像焦距f。对于相机坐标系下的任意一点P（Xc，Yc，Zc），图像坐标系下对应的点为p（x，y），由相机成像模型可知：

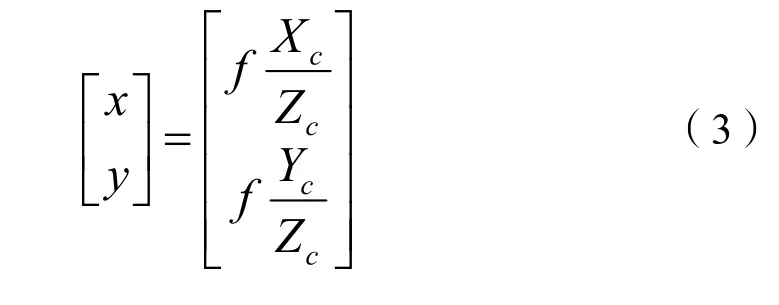
变换后得：

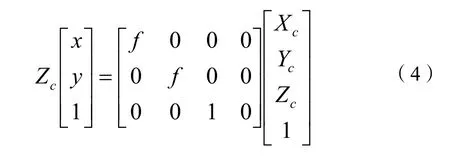
1.4 世界坐标系

世界坐标系表示为（Xw，Yw，Zw），也称为绝对参考坐标系，假设物理空间中一点在世界坐标系和相机坐标系下其次坐标分别为（Xw，Yw，Zw，1）T，（Xc，Yc，Zc，1）T，则它们之间的关系为：

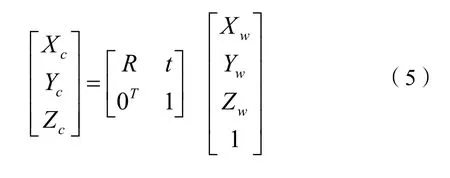
式（5）中：R、t分别为旋转矩阵和平移向量。

结合题意定义的世界坐标系是以光心为坐标原点，根据题目并结合自身分析需要，明确定义两坐标系之间不存在平移现象。将式（3）、式（4）代入式（5）可得世界坐标系与其他坐标系的转换关系：

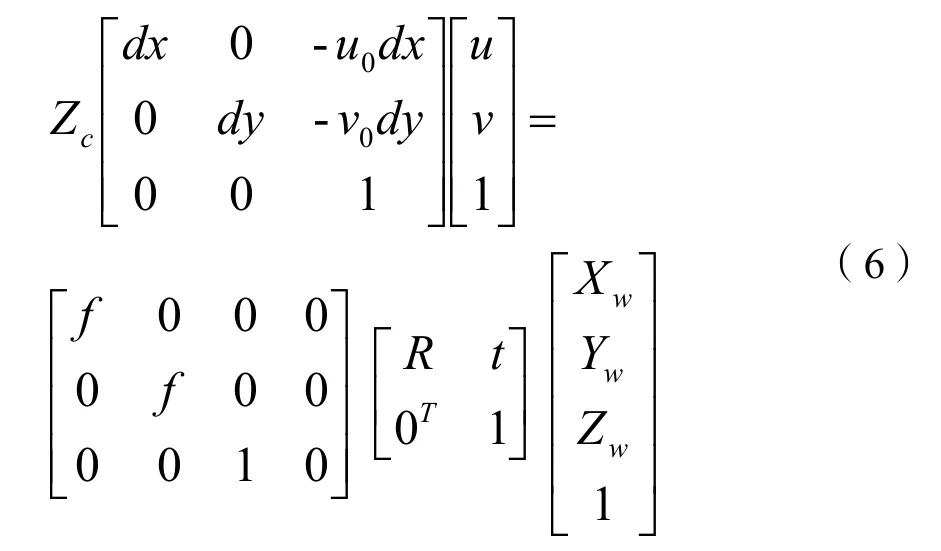
相机坐标系如图2所示。

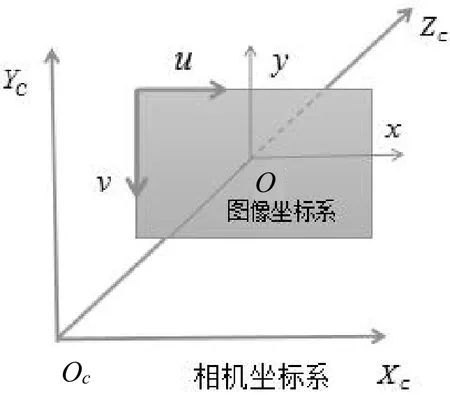
图2 相机坐标系

2 提取方法[5-7]

同一坐标系方向的平行直线的交点为图片的灭点，采用边缘检测算法，可以准确找到图片中所出现的直线，进而对直线上的关键点进行标定，从而计算出图片的灭点。Canny算法基于最优化算法的边缘检测算子，具有良好的信噪比和检测精度[6]，因此选取Canny算法进行图片边缘检测，然后用数学软件进行坐标标定，墙体部分边缘检测结果如图3所示。

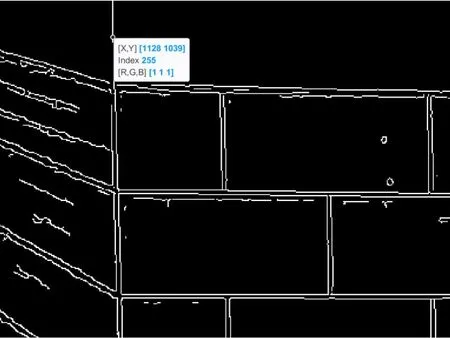
图3 墙体部分检测结果

通过边缘检测，在平行于坐标轴的3个方向上选取多个点进行标定，用数学软件找到点的坐标，然后联立直线的方程找图像的3个方向的灭点。

相机内参求取：根据灭点原理可知“连接灭点和垂心的相关的单位向量是两两正交”，假设3个灭点的坐标分别为（x1，x2，1）、（y1，y2，1）、（z1，z2，1），设O为3个灭点形成的三角形的垂心坐标O（u0，v0），VxP、VyP、VzP为相互正交向量，焦距f为OP的连线。则：

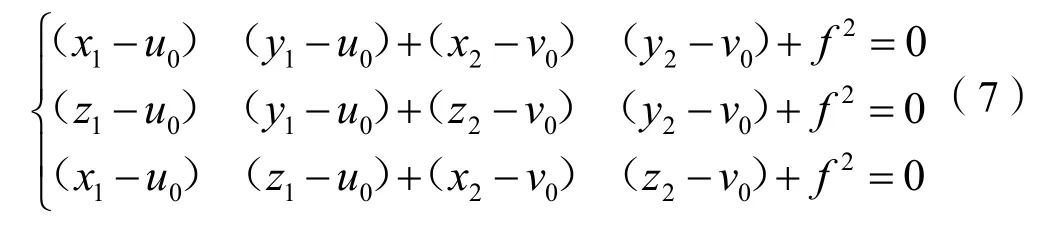
将已经求出的图片的灭点代入式（7）求取u0，v0、f。

旋转矩阵R求取：在世界坐标系下，令v1、v2、v3分别为与Fu、Fv、Fw这3个灭点相关的单位向量；V为由v1、v2、v3形成的3×3矩阵，其列向量分别为v1、v2、v3。在相机坐标系下，令分别为与Fu、Fv、Fw这3个灭点相关的单位向量；为由形成的3×3矩阵，其列向量分别为由灭点的属性可得，VRV＇= 。在世界坐标系中，灭点为3个方向上无穷远处的点，令这3个方向分别为世界坐标系的X轴、Y轴、Z轴方向，则有v1（1，0，0）、v2（0，1，0）、v3（0，0，1）。

因此，矩阵V为单位矩阵，又由VRV＇= 得：

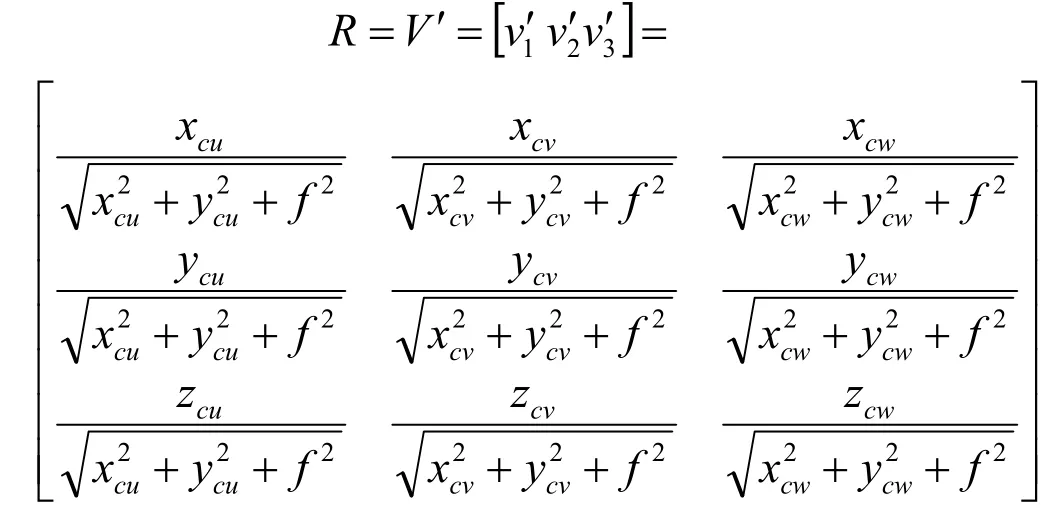
3 实验应用

热水器如图4所示，计算热水机的高度，先进行边缘检测。边缘检测如图5所示。

图4 热水器

图5 边缘检测

选取图片上与坐标轴平行的直线上面的点的像素坐标[8]，像素坐标如表1所示。

表1 像素坐标

表1（续）

计算灭点、内参、旋转矩阵，灭点如表2所示，内参如表3所示。

表2 灭点

表3 内参

旋转矩阵为：

点和距离如表4所示。

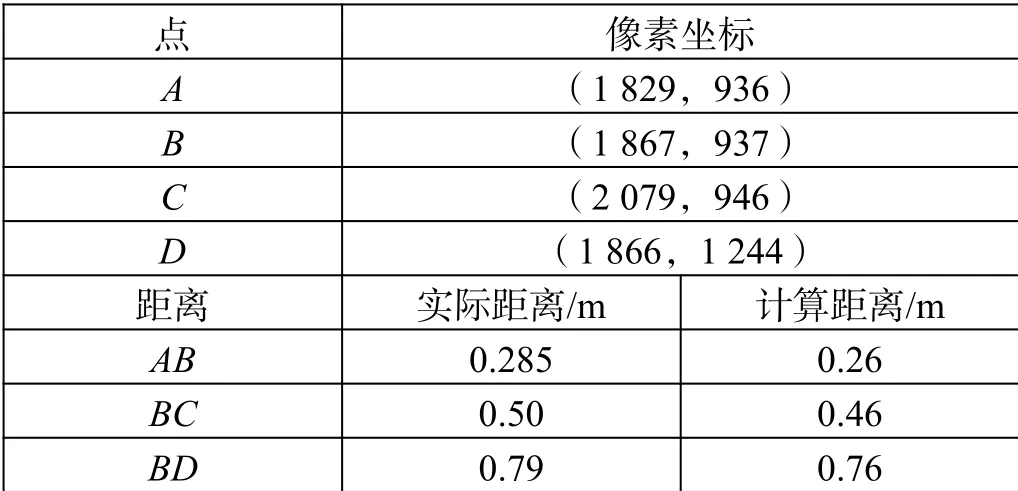
表4 点和距离

4 结论

基于单幅图片的信息提取，利用图像中的灭点进行相机标定，克服了传统图片信息提取过程中需要参照物来进行相机标定的复杂性；所采用的方法能够快速根据单幅图片中的直线寻找灭点，并求取图片灭点，进而得到相机内外参数，最终快速求取目标信息，具有很强的现实应用价值。