高速道岔轮轨力学行为研究
2022-06-26于淼
于淼
(中车大连机车车辆有限公司城铁开发部,辽宁 大连 116022)
高速道岔是高速铁路的关键设备,也是薄弱环节之一,近年来随着国内高速铁路的大规模建设,对其进行系统性研究显得更为迫切。目前,国内共铺设了5 000多组正线高速道岔[1],总体状态良好,但同样存在一些问题,例如道岔区几何参数超限导致车体异常晃动、尖轨心轨位移不足、曲尖轨磨耗以及表层接触疲劳、直尖轨非工作边裂纹、道岔区螺栓孔裂纹、扣件松动等[2]。
国内外对道岔轮轨动态相互作用方面的研究工作已开展很多年。SCHUPP等[3]研究了道岔区轮轨多点接触在多体动力学仿真中的实现方法。KASSA等[4]基于多体动力学软件GENSYS建立了列车/道岔动力学模型,研究关键参数随机输入情况下系统的动态响应。ALFI等[5]提出能够计算列车/道岔中频动态响应的数学模型,模型中考虑变截面钢轨及弹性轨道,并且根据现场试验实测数据验证了模型的正确性。SEBES等[6]运用多点赫兹接触理论建立道岔区的轮轨接触模型,结合多体动力学理论,分析列车通过可动心轨道岔时的接触斑位置、接触应力及等效应力等动态响应。王平等[7]基于轮轨系统动力学,结合道岔区轨道结构自身特点,研究了道岔区多点轮轨接触关系,建立了列车-道岔空间耦合动力学分析理论。任尊松[8]对车辆过岔时轮轨多点接触及车辆-道岔系统动态相互作用进行了研究。陈嵘[9]建立了完整的车辆-道岔-桥梁耦合振动模型,计算分析了列车通过桥上道岔时系统的振动响应,并进行了试验验证。全顺喜[10]分析了随机不平顺及实测不平顺对岔区轮轨耦合振动的影响,提出了岔区几何不平顺的控制限值和调整方法。
目前,利用列车-道岔耦合动力学理论分析高速列车与道岔动态相互作用仅限于低频时域范围[1]。本文将针对18号高速无砟道岔轮轨动力学行为进行研究,建立车辆-道岔刚柔耦合系统动力学模型,将轮对设为柔性体,利用功率谱密度和时频分析等方法分析列车过岔时的动态相互作用。
1 车辆-道岔系统动力学模型
选用某动车组及18号高速无砟道岔参数建立了车辆-道岔耦合系统动力学模型,如图1所示。
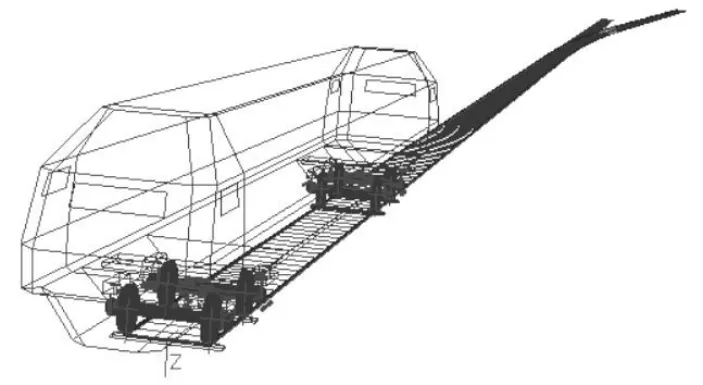
图1 车辆-道岔系统动力学模型
道岔区变截面模型由轨道纵向的若干特征截面通过线性插值得到,如图2所示。

图2 尖轨模型
尖轨区段轮轨静态接触几何如图3所示。

图3 转辙区轮轨静态接触几何关系
当尖轨宽0.02~0.03 m时,转辙区轮轨接触由基本轨过渡到尖轨。辙叉区心轨采用横向藏尖结构,分为长心轨和短心轨,基于同样方法获得辙叉区模型,如图4所示。

图4 辙叉区模型
护轨为分开式的33 kg/m槽型钢轨。道岔系统设有垂向、横向的刚度和阻尼。为了研究列车通过高速道岔时轮对的高频振动情况,将一位轮对设为柔性体,利用有限元软件进行联合仿真。取柔性轮对的前15阶模态,由于计算轮对模态时没有施加任何约束,所以前6阶为轮对的刚体模态,即刚体运动,所对应的固有频率为0,轮对振动频率如表1所示。

表1 柔性轮对各阶振动频率与模态
2 计算结果分析
本文主要研究道岔区轮轨接触几何改变对轮轨垂向作用力和轮对垂向加速度的影响,因此,分别对列车直向、侧向通过18号高速道岔时,轮轨间垂向作用力和轮对垂向加速度情况进行分析。
2.1 直向过岔
由于18号高速道岔的直向允许通过速度为350km/h,实际通过速度为300 km/h,所以,选取列车运行速度分别为270 km/h、290 km/h、310 km/h、330 km/h和350 km/h时的结果进行对比。不同速度下,列车直向过岔轮轨间垂向力如图5所示。
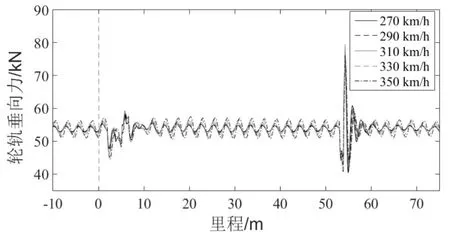
图5 直向过岔轮轨垂向力
由图5可知,由于车轴弯曲,在非转辙区和辙叉区段,轮轨垂向力出现周期小幅振动,随着速度增加,振幅略有增大。当速度为270 km/h时,振幅约0.8 kN;当速度为350 km/h时,振幅约2.7 kN,运行速度每增加20 km/h,轮轨间垂向作用力振幅增大不超过1 kN。直向过岔时,在转辙区,轮轨间作用力变化不明显,当距离尖轨尖端约7 m时,即尖轨宽度由0.02 m增大到0.05 m过程中,车轮完成了由基本轨到直尖轨的过渡,轮轨力先下降后上升,差值约14 kN;在辙叉区,在距离心轨理论尖端约1 m处,即心轨宽度在0.04 m左右,车轮完成了由翼轨到长心轨的过渡,轮轨力出现最大值,约为80 kN,是轮轨间静态垂向力的1.5倍,对心轨造成冲击。
不同速度下,列车直向过岔轮对垂向加速度如图6所示。
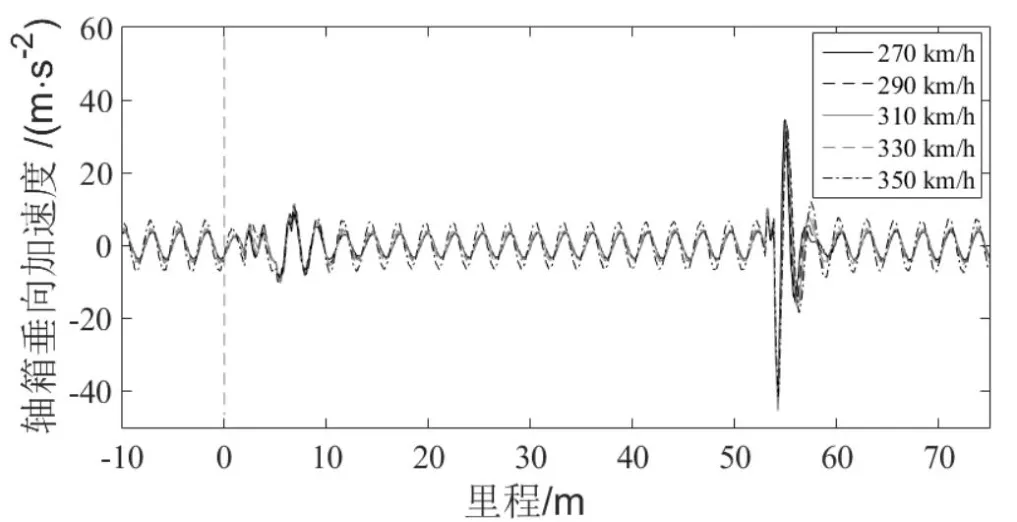
图6 直向过岔轮对垂向加速度
由图6可知,由于车轴弯曲,轮对垂向加速度出现周期小幅振动,振幅小于7 m/s2,随着速度增加,振幅略有增大,与轮轨垂向力的波动情况基本一致。直向过岔时,在转辙区,轮对垂向加速度变化不明显;在辙叉区,在距离心轨理论尖端约1 m处,即心轨宽度在0.04 m左右,车轮完成了由翼轨到长心轨的过渡,轮对垂向加速度达到最大值,取绝对值,约为45 m/s2,对心轨造成一定冲击作用。运行速度对道岔区轮对垂向加速度峰值的影响不大。因此,只选取310 km/h运行速度时的轮对垂向振动加速度结果,对其进行时频分析,如图7所示。

图7 直向过岔轮对垂向加速度时频分析
由图7可知,当以310 km/h速度直向过岔时,轮对垂向振动加速度的振动主频为31.9 Hz,同时在时频图中可以看到在30 Hz附近的一条光带,说明该频率存在于整个运行里程,与轮对转动频率基本一致,说明该主频是源于柔性轮对车轴的弯曲变形。直向过岔轮对垂向加速度高频段时频分析如图8所示。从图中可以看出,时频面能量在辙叉区较高,里程位置约为54 m,即轮轨接触由翼轨过渡到心轨的区段。该冲击引起轮对高频振动,而转辙区的冲击不明显。通过对轮对垂向加速度做200 Hz高通滤波,获取高频振动情况。

图8 直向过岔轮对垂向加速度高频段时频分析
由图8可知,轮对垂向加速度在高频区段,存在291 Hz的主频,且该频率覆盖了全部运行里程,而心轨对轮对的冲击主要激发了轮对300~500 Hz的高频振动,且能量主要集中在300 Hz左右。对照表1中柔性轮对各阶振动频率,其中,第12阶模态对应的振动频率为296.93 Hz,为轮对的对称伞型模态。第13阶和第14阶模态对应的振动频率为316.12 Hz,分别为轮对的3次水平和垂向弯曲模态。
车轮在心轨处的冲击引起的轮对振动加速度主频与这三阶模态对应的固有频率相接近,易引起轮对对称伞型和3次弯曲模态的复合振动,由于模态阶数较高,能量相对较小。
2.2 侧向过岔
由于18号高速道岔的侧向允许通过速度为80 km/h,所以,选取列车运行速度分别为60 km/h、70 km/h、80 km/h、90 km/h时的结果进行对比。列车侧向过岔时,轮轨接触情况相对直向过岔复杂。侧向过岔时,轮轨接触在转辙区由基本轨过渡到曲尖轨,在辙叉区由翼轨过渡到长心轨,接着由长心轨过渡到短心轨,最后通过短心轨末端的滑动接头。
不同速度下,列车侧向过岔轮轨间垂向力如图9所示,轮轨垂向力峰值如图10所示。

图9 侧向过岔轮轨垂向力

图10 侧向过岔不同速度下轮轨垂向力峰值
由图9可知,由于运行速度较慢,由柔性轮对车轴弯曲引起的轮轨垂向力周期振动不明显。侧向过岔时,18号道岔存在半径为1 100 m的圆曲线,且直线和圆曲线之间没有缓和曲线过渡,轮对冲角较大,所以位于圆曲线初始位置的曲尖轨部分会受到较大冲击。且随着运行速度的增加,轮轨接触由基本轨过渡到尖轨时的冲击力越大,由于离心力作用,圆曲线区段轮轨间作用力也逐渐增大。在辙叉区,轮轨间垂向力出现3个振动峰值,分别对应轮轨接触由翼轨过渡到长心轨,由长心轨过渡到短心轨,再通过滑动接头。
由图10可知,同一速度下,尖轨处的轮轨垂向力峰值大于长心轨、长心轨大于短心轨、短心轨大于滑动接头,尖轨处垂向力峰值较大主要是由于过渡区位于道岔圆曲线初始位置,车轮与尖轨发生接触时更接近于车轮轮缘。而长心轨、短心轨、滑动接头的尖端角度递增,使得过渡区的轮轨接触逐渐趋于车轮踏面中部,使得垂向力峰值降低,冲击减小。
不同速度下,列车侧向过岔轮对垂向加速度波形基本相似,当列车运行速度为80 km/h时轮对垂向加速度如图11所示,不同速度下轮对垂向加速度峰值情况如图12所示。

图11 侧向过岔轮对垂向加速度

图12 侧向过岔不同速度下轮对垂向加速度峰值
由图11可知,轮对垂向振动加速度基本上是以X轴为中心轴上下振动,不同于轮轨垂向力受曲线离心力的影响,振动波形存在趋势项。由于车轴弯曲,轮对垂向振动加速度出现周期小幅振动,振幅小于1 m/s2。侧向过岔时,在转辙区,同样由于离心力作用,当轮轨接触由基本轨过渡到曲尖轨时,即距离尖轨尖端约4 m处,轮对垂向加速度出现振动峰值,约为46 m/s2,振动方向向上;在辙叉区,出现的3个振动峰值分别在距离心轨理论尖端约0.4 m、2 m、9.5 m,冲击钢轨。由图12可知,随着速度增加,轮对垂向加速度峰值逐渐上升,且同一速度下尖轨处的峰值大于长心轨、长心轨大于短心轨、短心轨大于滑动接头处,与轮轨垂向力的规律一致。其中,在列车运行速度为60 km/h和70 km/h时,短心轨处的峰值略大于滑动接头。对列车运行速度为80 km/h时轮对垂向振动加速度进行时频分析,如图13所示。

图13 侧向过岔轮对振动加速度时频分析
由图13可知,侧向过岔时,轮对垂向加速度有多个振动主频,功率谱密度最大的主频为8.203 Hz,近似于运行速度为80 km/h的轮对转动频率8.225 Hz,该主频为轮对转动的固有频率,是由柔性轮对车轴弯曲引起。由于运行速度较低,在时频图中对应频率的能量不是很明显。从功率谱中可以看出在250~350 Hz之间,出现轮对振动加速度的高频振动主频,约为298.4 Hz,结合时频图可知,时频面能量在转辙区较高,里程位置约为4 m,即轮轨接触由基本轨过渡到曲尖轨。同样,该冲击引起轮对振动加速度主频与轮对第12、13、14阶模态对应的固有频率相接近,易引起轮对对称伞型和3次弯曲模态的复合振动。而辙叉区的冲击不明显,3个振动峰值对应的里程位置处的时频面能量较小。
3 结论
将轮对设为柔性体,可获得轮对高频振动情况,由于车轴两端在轴重载荷下弯曲变形,致使轴端的中心点不在轮对转轴的中心线上,在列车运行中,轮轨力和轮对振动加速度会出现幅值随列车运行速度变化的等幅振动,且振动频率与轮对转动频率一致。
直向过岔时,车轮在辙叉的区作用力相对于转辙区明显,对长心轨宽约0.04 m处冲击较大;侧向过岔时,车轮对转辙区作用力相对于辙叉区明显,对曲尖轨宽约0.02 m处冲击较大,且随着运行速度的加快,轮轨间垂向力和轮对垂向加速度均逐渐上升,同一运行速度下,尖轨处的峰值大于长心轨、长心轨大于短心轨、滑动接头处最小。
直向过岔时车轮对长心轨的冲击以及侧向过岔时对曲尖轨的冲击均激发了轮对垂向加速度300 Hz左右的高频振动,接近于轮对的固有频率,易引起轮对对称伞型和3次弯曲模态的复合振动。
