基于无迹卡尔曼滤波的海上风机叶片吊装控制

郭佳民　谢雨阳　 赵宇　侯先瑞　宋力

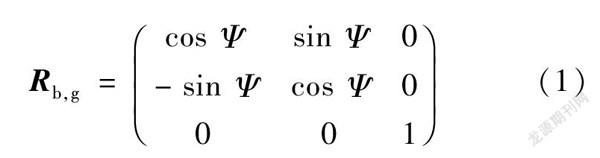
摘要：为提高海上风机单叶片在风荷载作用下的吊装效率与精度，构造单叶片的吊装运动系统。设计无迹卡尔曼滤波与PID控制相结合的主动闭环控制系统，模拟单叶片按照3种预期路线进行110 m的吊装控制。分析结果表明，引入无迹卡尔曼滤波不仅可以明显减少吊装过程中由风荷载所致的干扰振荡，有效提高吊装效率，还可以降低缆风绳控制力的变化率，降低硬件设备的速度响应要求。建议在吊装过程中降低缆风绳的控制力。

关键词：  海上风机; 叶片吊装; 运动方程; 无迹卡尔曼滤波;  PID控制

中图分类号：  P752; TK83文献标志码：  A

Blade hoisting control of offshore wind turbines

based on unscented Kalman filter

Abstract： In order to improve the efficiency and accuracy of hoisting a single blade of offshore wind turbines under wind load， a singleblade hoisting motion system is constructed. An active closedloop control system combining the unscented Kalman filter and PID control is designed to simulate a single blade to be controlled for 110 m hoisting according to three expected routes.The analysis results show that， the introduction of the unscented Kalman filter can not only significantly reduce the disturbance and vibration caused by wind load during hoisting and can improve the efficiency of hoisting， but also reduce the change rate of the control force of the tugger line and the speed response requirement of hardware devices.It is recommended to reduce the control force of the tugger line during hoisting.

Key words： offshore wind turbine; blade hoisting; equation of motion; unscented Kalman filter; PID control

引言

風能资源的开发利用是我国调整电力结构的重要举措之一。与陆上风电场相比，海上风电具有占用土地资源少、风速较大、持续时间较长、风能利用率高等优点[1]。海上风能发电作为一种安全稳定又环保的能源建设方式，近年来得到了社会各界的普遍关注。2020年7月，中国自主研发的容量为10 MW的海上风机正式下线，其叶轮直径达185 m。细长的风机叶片在吊装时极易受到风荷载的干扰[2]。为提高风电的产能，风场往往位于风速较大的海域，但叶片因其自身几何形状复杂、刚度较低、质量较轻，只能在风速低于12 m/s时才能吊装[3]，这将采用昂贵吊装设备（安装船、起吊机）和增加船员的吊装等待时间，导致吊装成本的增加。因此，在海上风场建设过程中如何降低叶片安装对风速的限制以及提高安装效率是研究人员与工程人员普遍关注的问题[4]。为解决叶片长度和体积的增加带来质量增加的问题，叶片的刚度进一步降低，但这让叶片更易受损[5]。因此，提高叶片吊装的稳定性是降低风速限制的关键内容。研究人员已在吊装辅助工具开发和吊装控制方法两个方面展开了研究。吊装方案设计者期望通过多个辅助工具的参与来减少叶片在风和吊索作用下的摆动，LT575 Blade Dragon和Boom Lock等叶片吊装辅助工具先后被开发出来。然而，传统的叶片吊装方法对人力依赖程度较高，吊装精度低，稳定控制效果差。研究人员借鉴起重机吊装作业时采用自动控制方法减少货物空中摆动的成功经验[67]，尝试通过自动控制方法来提高叶片的吊装精度，提高吊装效率。REN等[89]首次采用扩展卡尔曼滤波（extended Kalman filter，EKF）与比例积分微分（proportionalintegralderivative，PID）控制相结合的方法，达到了对叶片精准控制的效果，降低了叶片的对位难度。自动控制方法的引入推动了叶片吊装控制的进步。但EKF在计算时直接采用泰勒展开的一阶项对非线性系统进行线性化，引入了较大的截断误差，势必将导致计算精度下降。此外，REN等[89]设计的控制系统对缆风绳主动控制力的输出响应要求较高，这将增加控制系统中硬件设备的投入，不利于其推广应用。本文采用精度较高的无迹卡尔曼滤波（unscented Kalman filter，UKF）来构造叶片的吊装控制系统，提高吊装精度，并降低对控制系统中缆风绳主动控制力的响应要求。而UKF与PID相结合的控制系统目前已经在车辆自动巡航系统领域得到了广泛应用[10]。

本文首先建立单叶片吊装的运动方程，并以此建立UKF的状态方程和测量方程，然后构造出PID控制器，最后形成包含叶片吊装实际路径和受力情况的模拟系统、叶片观测系统、滤波器以及控制器的闭环控制反馈系统，并对单叶片的吊装进行模拟。研究结果表明，UKF与PID结合可精确控制叶片的提升过程，较EKF具有精度高、操作简便的优点，且UKF能够明显降低缆风绳主动控制力的变化率。这将降低对整个控制系统中硬件设备的响应要求，进而可降低整个控制系统的造价，方便其推广应用。

1单叶片吊装运动系统

单叶片起吊方法可提高运输船的甲板空间利用率，降低起吊机的载重能力要求，每个叶片从运输平台上水平起吊、提升、对位插入轮毂后将轮毂旋转120°再开始下一个叶片的吊装[11]。如图1所示：叶片通过夹具与吊索相连，并由卷扬机进行提升;夹具的夹点对称于叶片的重心布置;由铰机控制的两根缆风绳通过对其控制力的实时调整来减少风荷载导致的叶片摆动，确保叶片按预定路线和姿态进行提升。为便于描述叶片位置姿态，假定吊装过程中缆风绳、叶片和夹具同步上升，且在控制系统作用下缆风绳与水平面的夹角保持不变。吊装过程中叶片的受力情况和坐标系可简化为图2，其中：整体坐标系Ogxgygzg的原点位于卷扬机的顶点处，xg轴与主风向相同，zg轴竖直向下，yg轴由右手法則确定;随体坐标系Obxbybzb的原点设置在叶片的重心处，yb轴由叶片尾部指向顶端，zb轴竖直向下，xb轴由右手法则确定。由于夹具的应用，叶片可看作刚体[9]，吊装过程中叶片绕xg轴和yg轴的旋转可以忽略，仅需考虑叶片的3个线位移和绕zg轴的角位移。在随体坐标系和整体坐标系（1）式中：Ψ为xb轴与xg轴的夹角。

如图2所示，作用在叶片上的荷载有重力mg、风荷载τw、缆风绳的控制力U=（u1，u2）以及吊索的提升力T。其中，重力由叶片重力mbg、钩子重力mhg和夹具重力myg三部分组成。本文仅考虑叶片匀速提升的情况，因此只考虑风荷载垂直作用于叶片表面的水平力，而忽略其产生的竖向浮力。依据横流原理＼[3＼]，在随体坐标系中叶片上的风荷载fwx、

fwy、 fwz以及绕z轴的变矩Mw可由如下公式获得：

（2）

（3）

（4）

式中：i为叶片分割后的第i段;ρ为空气密度;ti、i、Cd（ti）分别是第i段的中心厚度、与横摇角度β相应的攻角、气动阻力系数;Ci为弦长;Ri为从第i段截面中心到叶片重心的距离;vw为作用在叶片上的风速。本文采用改良后的组合风模型＼[12＼]（即风速由基本风vba、阵风vgu、渐变风vgr、随机风vra四部分叠加而成），考虑到风速仪通常安装在夹具上，本文用高斯白噪声ww表示模拟位置与测量位置不一致所导致的风速测量误差，每一时刻的风速计算公式为（5）基本风速vba在实际吊装过程中随时发生变化，为此首先确定标准参考高度10 m处的基本风速，然后采用如下公式进行实时高度处基本风速的计算：

（6）

（7）

式中：kz为本海域的高度换算系数;v10为标准高度（10 m）处的基本风速;zg为实际高度;Z0为本海域内海面波浪的状态系数，其取值以7 m/s风速（风力4级）为界，当风速大于等于7 m/s时Z0=0.022，当风速小于7 m/s时Z0=0.023。

vgu在阵风存在的时间段内取0.5vgu，max（1-cos（2π（t-T1）/Tgu）），在其他时间段内取0，这里T1是阵风开始的时刻，Tgu是阵风持续的时长，vgu，max是阵风速度最大值，一般vgu，max=0.05vba。vgr通常在渐变风变化时间段（Tc1，Tc2）内取vgr，max（t-Tc1）/（Tc2-Tc1），在渐变风稳定时间段（Tc2，Tc2+Tc）内取vgr，max，在其他时间段内取0，一般vgr，max=0.08vba。vra=vn，maxRamcos （ωnt+φn）。本文中ωn=1.6π，φn为一随机变量，通常取（0，2π）之间的随机数，vn，max=0.1vba。Ram为（0，1）内的随机数。

如图2所示，缆风绳的平面投影与整体坐标系的xg轴平行，与Ogxgyg平面的夹角为θ，叶片重心到缆风绳1和2的力臂分别为r1和r2，则缆风绳控制力U简化到叶片重心处的等效合力在整体坐标系上的投影向量为（8）其中为叶片吊装系统中的主动控制输入值，其大小由控制器根据叶片的实际受力、姿态和期望姿态等确定。

当叶片匀速提升时，提升力T在zg轴上的分量为Tz=-mg+Fz，其中m=mb+mh+my。由于叶片的重心在吊索的轴线上，所以提升力T对叶片无任何旋转分量。吊索的提升力T在整体坐标系上的投影向量可表达为m为叶片质量mb、钩子质量mh和夹具质量my的总和，

（9）

式中：xcog、ycog、zcog为叶片重心在整体坐标系x、y、z轴上的坐标分量。

在整体坐标系下叶片4个自由度的刚体运动方程可表达为（10）式中：M=diag（m，m，m，Ib），Ib为叶片绕zb轴的转动惯量;b=（b1，b2，b3，b4）T，用来估计由预应力、模型不确定性、环境干扰等因素引起的叶片上荷载的偏差。b满足如下表达式： （11）式中：Tb=diag（Tb1，Tb2，Tb3，Tb4）是一个调整矩阵，其中Tb1、Tb2、Tb3、Tb4均为大于零的实数，在整个模型设计建立阶段可进行调整;wb=（wb1，wb2，wb3，wb4）T，用来模拟过程噪声，是b的激励矩阵。

叶片在不同坐标系下的速度向量关系为（12）则叶片的运动方程（式（10））在随体坐标系下可表达为

（13）

式（10）和（13）即为单叶片吊装运动系统方程。

2滤波系统设计

卡尔曼滤波理论主要用于过滤测量误差，并结合对下一时刻状态的估计（先验估计），得到一个相对于测量值更接近真实值的预测值（后验估计）。EKF算法在线性化过程中引入了截断误差，降低了滤波效果，也可能导致最终滤波结果的发散;UKF采用无迹变化的方法处理滤波器中均值和协方差非线性传递问题，能够避免EKF中忽略高阶项所带来的误差，对于非线性系统具有较高的计算精度＼[13＼]。本文采用这一算法处理强非线性的叶片吊装问题。

依据上文的吊装运动系统方程，假定叶片吊装过程中具有高斯白噪声W（k）的状态向量为X（k）=Xg，b，dXgdt，DwT，具有高斯白噪声V（k）=（vx，vy，vz，vΨ，vDw）T的观测向量为Y（k）=（Xg，Dw）T，则在k时刻可构造出如下的状态方程和测量方程：（14）其中，f为非线性状态方程函数。这里的X（k）为叶片吊装运动系统k时刻的真实输入值，而U（k）由控制器k时刻的计算值输入，W（k）和V（k）的协方差阵分别为Q和R，H为非线性观测方程函数。在叶片吊装过程中，仅观察叶片的位置姿态Xg和作用在叶片上的风速Dw，因此观测矩阵具体可表达为

（15）

假定式（14）中的状态向量X的维数为n，均值为X，方差为P。为处理滤波器中均值和协方差非线性传递的问题，本文采用无迹变化公式得到2n+1个sigma采样点Xi，也可求得状态向量的均值与方差对应的权值wm，i、wc，i。用头上带“^”的向量符号表示向量的预测值。

（16）

（17）

（18）

式中：λ为一个可调整的比例缩放参数，用来降低总的预测误差，λ=2（n+δ）-n;为控制采样点分布状态的控制参数;ζ为一个大于等于零的权系数;δ为待选参数，其取值须保证（n+λ）P为半正定矩阵。经过多次试验本文取=1，ζ=0，δ=2。

k时刻状态向量X的2n+1个采样点为

（19）

分别计算sigma点集和状态向量的一步预测，并求得协方差矩阵：

（20）

（21）

（22）

再次使用无迹变换，求得k+1时刻的采样点集Xi（k+1k）。

将上述点集代入观测方程，可求得观测量Y（k）的预测值及预测值对应的均值和协方差：

（23）

（24）

（25）

（26）

卡尔曼增益矩阵可依据下式进行计算：（27）状态向量和协方差矩阵的更新计算式为

（28）

（29）

式（16）～（29）即为进行叶片吊装的无迹卡尔曼滤波器。每一时刻计算得到的状态向量的预测值都将传递给下文的控制器，用于计算缆风绳的控制力U。

3控制系统设计

由式（10）和（13）可知，叶片吊装过程中的姿态主要通过缆风绳控制力U的实时调整实现。因此，需设计一个合理的控制器，依据叶片的实际位置Xg与预期位置Xd之差及叶片受力情况实时计算缆风绳的控制力并通过铰机实现，保证叶片沿预定路线吊装。本文采用PID控制叶片的吊装，具体思路见图3。

在吊装过程中假定各个方向上的变量均可被独立控制，由式（10）和（13）可知，整个叶片吊装系统简化模型是一个四自由度二控制输入的欠驱动系统。为此，本文仅考虑风荷载的水平分力和叶根处的水平运动。为了在控制系统中仅保留叶片的2个自由度，本文通过投影矩阵L=1000

0001对单叶片吊装运动系统中位姿Xg的4个自由度进行取舍计算。由无迹卡尔曼滤波器获得的叶片位置预测值的误差为e=Xg-Xd。利用投影矩阵L将四自由度模型转化为一个只有受控状态量的简化形式，其中e的二阶导数满足 （30）依据PID理论，假定系统的控制量计算式为 （31）式中：Kp、Kd和Ki分别为比例、微分、积分系数矩阵，主要进行平衡系统的动态性能和稳态性能的调整。设置合理的系数可得到一个稳定性强、响应速度快、调节时间少的控制器。Kp、Kd和Ki的公式如下：

其中λx和λψ为x和ψ方向上的控制参数特征值。由叶片运动方程式（10）和（13）及滤波器的叶片姿态预测方程式（28）和（29）可得出缆风绳的控制力计算公式：

（32）

反复利用式（10）、（13）、（28）、（29）和（32）即可主动控制叶片的吊装过程。

4数值模拟

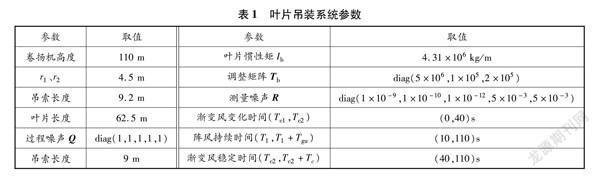
本文数值模拟在MATLAB/Simulink中完成。依据上文的叶片吊装运动系统、滤波系统和控制系统的基本理论建立单叶片吊装模拟闭环控制系统，叶片吊装模拟流程见图4。模拟系统包括模拟器、测量器、滤波器和控制器4个模块。模拟器模块根据叶片受力、运动方程模拟叶片吊装过程中的位置姿态的真实值，并输出到测量器。测量器通过添加噪声的方法模拟实际吊装中的观测值，并将结果输入滤波器模块。无迹卡尔曼滤波器对观测值过滤后得到预测值，然后将预测结果输入控制器计算所需的控制力。最后将控制力的计算结果反馈输入给模拟器模块，进行下一时刻的叶片受力分析。本文模拟一长度为625 m的叶片历时110 s的吊装过程，叶片质量mb=1774 t，钩子质量mh=1 t，夹具质量my=50 t。为防止缆风绳在吊装过程中松弛，确保其对叶片的有效控制，吊装模拟过程中叶片逆风向偏移25 m，即叶片的提升轨迹设定为xd=-2.5 m，yd=0，Ψd=0，同时叶片以-1 m/s的速度匀速上升。假定叶片对位时风机轮毂（即最终对位目标点）保持静止，在缆风绳的控制下叶片与卷扬机和吊索保持相对静止。本文所用叶片模型、滤波器和

控制器的部分参数见表1。控制系统中部分参数经过多次试算取值为：kp=0.534 2，kd=1，ki=1，λx=λφ=1。本模拟系统的参数选取来源于NREL 5兆瓦叶片＼[14＼]。

在整体坐标系下，叶片从甲板zg=110 m开始起吊，当叶片提升到zg=0时开始对位。假定标准高度10 m处的基本风速v10为10 m/s＼[15＼]，基于组合风速模型的基础理论依据式（5）模拟不同高度处的风速，在结果中加入方差为0.01的高斯白噪声来模拟此过程中风速的观测结果。吊装过程中垂直作用在叶片上的风速模拟结果见图5。第10 s时，作用在叶片上的风速vw=vba+vgu+vgr+vra=（10+0.25+0.2+0.210 4）m/s=10.660 4 m/s。

整个吊装模拟过程采用的时间步长为0.01 s，提升过程中由吊装模拟系统得到的缆风绳控制力和叶片姿态的变化规律见图6。

由图6可以看出，吊装过程中缆风绳的控制力随外部风荷载的变化而变化。当zg方向仅考虑叶片受风的影响在水平方向上振荡引起高度变化时，叶片可以以-1 m/s的速度在110 s时到达对位高度（zg=0），且叶片经过起吊开始阶段（0～5 s）的振荡后，其xg方向的姿态也基本穩定在-2.5 m的位置上。总体来说，本文设计的吊装控制系统可以保证叶片以预定的路径完成提升。由图6也可以看出，吊装起步时叶片从初始位置到达目标位置的过程中，其姿态与缆风绳的控制力会有一定的瞬态效应。

為详细了解UKF在控制系统中的效果，本文提取了100～110 s期间较为稳定的叶片姿态测量值、真实值和滤波结果进行对比，见图7。

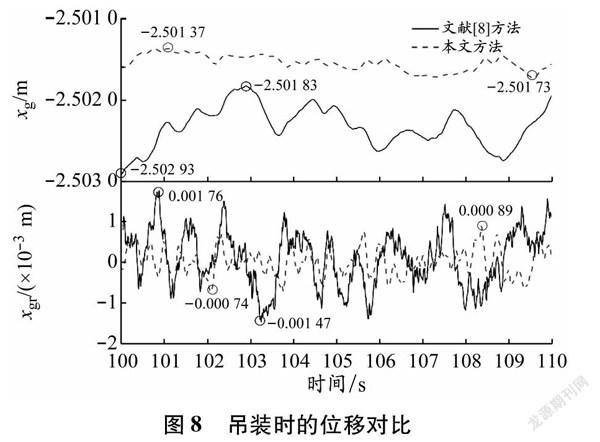
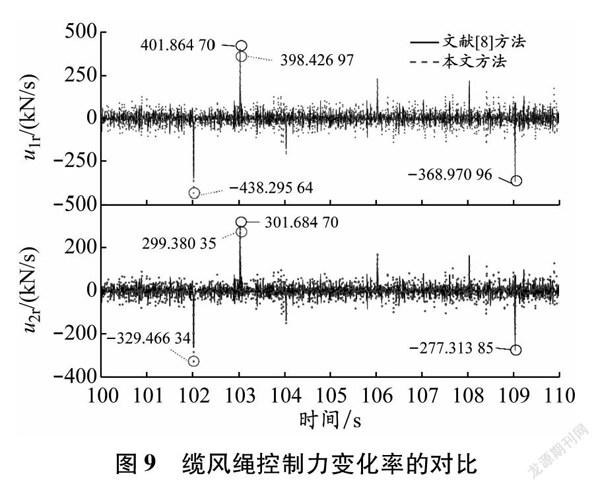
由图7可知，UKF对风荷载中添加的白噪声起到了很好的滤波效果，叶片姿态的实际值与预测值更为接近。同时可以看出，在稳定阶段，叶片在xg方向上基本以1×10-3 m的幅值在-2.5 m的附近振动，在yg和ψg方向上几乎没有振动（其振幅的数量级均为10-5 m），这说明上文在设计控制器时不考虑yg方向上运动的简化方法是合理可行的。外部风荷载和缆风绳控制力u1和u2均在xg方向上，这是导致叶片在xg方向上的位移振幅几乎为yg方向上或ψg方向上100倍的主要原因。在后续讨论中，本文仅取叶片振幅较大的xg方向上的位移来分析叶片的位置姿态。为进一步了解UKF与PID结合这一方法的控制精度及控制稳定性，本文将模拟结果与文献＼[8＼]的方法（EKF与PID结合）进行对比，结果见图8和9。此外，叶片振动速率的大小与叶片对位安装时的难度直接相关，而缆风绳控制力的变化率与控制系统的响应速度要求也直接相关。响应速率大的硬件系统造价高，其实际工程应用的推广难度高。为此将叶片姿态的变化率xgr与缆风绳控制力变化率u1r、u2r的结果进行对比，结果见图8和9。

对位前叶片与轮毂保持相对稳定是必要的。由图8可以看出，本文方法较文献[8]方法的精度明显提高，最大误差从0.002 93 m降低到0.001 73 m，降幅达41.9%，这说明UKF系统的控制精度更高。从xg方向上位移曲线及其变化率的计算结果可以看出，UKF系统的控制平稳性也更好，不但变化率的最大值由0.001 76降低到0.000 89，而且位移及其变化率的离散性也得到明显改善，这说明UKF系统的稳定性优于EKF系统的稳定性。

铰机等硬件设备的造价与其响应速度密切相关，为此本文对不同系统下缆风绳控制力的变化速率进行对比，从而了解不同控制系统对铰机响应速度的要求，以便评估铰机等硬件设备的造价。由图9可以看出，使用UKF系统时缆风绳控制力变化率的离散性也明显得到改善，这将降低对吊装控制系统硬件设备技术水平的要求，进而将降低控制系统的造价，有利于叶片吊装系统的推广应用。同时u1r的幅值也得到降低，但u2r的幅值在102 s时小幅上升，这可能与缆风绳控制力u2较小有关。总体来说，UKF与PID结合可圆满实现叶片的吊装控制，且控制精度和稳定性好。

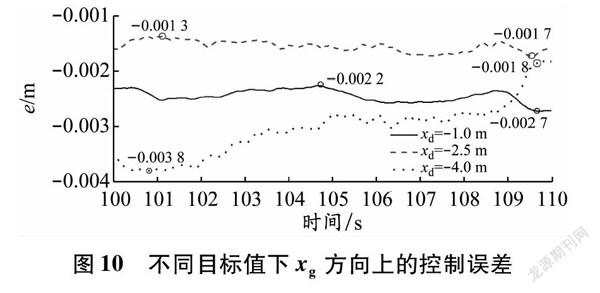
叶片在提升过程中的位置姿态与缆风绳控制力大小密切相关，缆风绳控制力较大时不易出现松弛失控的现象，但会增加缆风绳端部铰机的负担。为此本文选取xd分别为-1.0 m、-2.5 m、-4.0 m时的3种不同吊装目标路径，并对比xg方向上的控制误差e和缆风绳的控制力变化率，结果分别见图10和11。

由图10图可知：当xd=-1.0 m时，叶片的最大控制误差为-0.002 7 m;当xd=-2.5 m时，叶片的最大控制误差为-0.001 7 m;当xd=-4.0 m时，叶片的最大控制误差为-0.003 8 m。3种情况下的控制误差均为10-3数量级，说明在目标值发生改变时，整个控制系统依旧可以按照预期路线完成提升且保持稳定。

由图11可知，当目标值xd从-1.0 m降低到-4.0 m时，u1r最大绝对值由389.131 kN/s增加到426.966 kN/s，而u2r最大绝对值由292.288 kN/s增加到321.004 kN/s。当风速和上升速度保持一致时，随着目标值的降低，缆风绳的控制力增大。因此，在叶片提升过程中缆风绳控制力的增大不仅会增加铰机的负担，而且会提高对铰机响应速度的要求，提升过程中在保证缆风绳不松弛的条件下应降低其控制力的大小。

5结论

本文提出由UKF与PID相结合的闭环控制系统，并在模拟风场内验证了其可行性。结论如下：

（1）UKF与PID相结合的叶片吊装控制系统可依据预定吊装路线完成对叶片的提升控制。提升开始后叶片在5 s内即可基本稳定在预定姿态下，之后叶片在目标路径上小幅波动并到达目标位置。

（2）与EKF与PID的组合相比，UKF与PID的组合在控制精度与控制稳定性方面更好，叶片振动幅值有效减小，这使得叶片对位的难度大大降低。缆风绳控制力的变化率也得到了改善，这有助于降低对控制系统中硬件设施响应速度的要求，进而可扩大控制系统的应用范围。通过结果分析还发现，在提升过程中，叶片的目标姿态偏离竖直方向越大，缆风绳的控制力越大，且缆风绳的控制力变化率也越大，这将提高对铰机在负荷和响应方面的要求。因此，叶片目标姿态的设定，应在保证缆风绳不松弛的情况下，减少其偏离竖直方向的大小。

本文假定叶片对位时轮毂保持静止不动，在实际工程中轮毂随外部周期荷载会发生小幅振动，如何让叶片在对位过程中与运动的轮毂保持一致是需要继续研究的问题。本文提出的这一系统可直接写入单片机，与传感器相结合即可应用于实际工程，这也是日后需要继续研究的内容。

参考文献：

[1]史军， 徐家良， 穆海振. 上海近海海上最大风速的估算及数值模拟[J]. 太阳能学报， 2017， 38（4）： 991998.

[2]WANG Y F， LIANG M， XIANG J W. Damage detection method for wind turbine blades based on dynamics analysis and mode shape difference curvature information[J]. Mechanical Systems & Signal Processing， 2014， 48（1/2）： 351367. DOI： 10.1016/j.ymssp.2014.03.006.

[3]GAUNAA M， BERGAMI L， GUNTUR S， et al. Firstorder aerodynamic and aeroelastic behavior of a singleblade installation setup[J]. Journal of Physics Conference， 2014， 524（1）： 012073. DOI： 10.1088/17426596/524/1/012073.

[4]陶钢正， 王建国， 冯江哲. 1.5 MW风电机组单叶片吊装专用吊梁设计[J]. 风能， 2012， 11（1）： 9296.

[5]张兴伟， 陈严. 风力机大型化发展中的总体设计技术[J]. 新能源进展， 2013， 1（3）： 218223. DOI： 10.3969/j.issn.2095560X.2013.03.003.

[6]FANG Y C， WANG P C， SUN N， et al. Dynamics analysis and nonlinear control of an offshore boom crane[J]. IEEE Transactions on Industrial Electronics， 2014， 61（1）： 414427. DOI： 10.1109/TIE.2013.2251731.

[7]MASOUD Z N， NAYFEH A H， MOOK D T. Cargo pendulation reduction of shipmounted cranes[J]. Nonlinear Dynamics， 2004， 35（3）： 299311. DOI： 10.1023/B：NODY.0000027917.37103.bc.

[8]REN Z R， JIANG Z Y， GAO Z， et al. Active tugger line force control for single blade installation[J]. Wind Energy， 2018， 21： 13441358. DOI： 10.1002/we.2258.

[9]REN Z R， JIANG Z Y， SKJETNE R， et al. Development and application of a simulator for offshore wind turbine blades installation[J]. Ocean Engineering， 2018， 166（1）： 380395. DOI： 10.1016/j.oceaneng.2018.05.011.

[10]翟志強， 许进亮， 袁皓， 等. 自适应巡航系统车辆跟驰控制策略仿真[J]. 系统仿真学报， 2020， 32（5）： 885891. DOI： 10.16182/j.issn1004731x.joss.180646.

[11]韩志鹏. 风电机组单叶片吊具性能分析[J]. 科技经济导刊， 2019， 27（5）： 4243.

[12]谭婕， 汪学峰. 海洋风速动态仿真及其在平台模拟系统中的应用[J]. 中国造船， 2014， 55（1）： 150157.

[13]袁国刚， 陈鹏， 王永川， 等. EKF、UKF、PF混沌同步性能分析[J]. 计算机工程与设计， 2019， 40（7）： 18351839. DOI： 10.16208/j.issn10007024.2019.07.006.

[14]JONKMAN J M， BUTTERFIELD S， MUSIAL W， et al. Definition of a 5MW reference wind turbine for offshore system development[R]. US： National Renewable Energy Laboratory （NREL）， 2009. DOI： 10.2172/947422.

[15]时军. 海洋平台上的风载荷计算研究[D]. 大连： 大连理工大学， 2008.

（编辑贾裙平）

收稿日期： 20210122修回日期： 20210406

基金项目： 国家自然科学基金（51108259，52001198）

作者简介： 郭佳民（1979—），男，内蒙古呼和浩特人，教授，博导，博士，研究方向为索杆结构的施工建造，（Email）jmguo@shmtu.edu.cn