Orbifold Fundamental Group and Deck Translation Group
2022-06-25-
-
( School of Financial Mathematics and Statistics, Guangdong University of Finance,Guangzhou 510521, China )
Abstract: In this paper, we define the notions of orbifold loop and orbifold road, with which, we reformulate the definition of orbifold fundamental group and deck translation group. We show that, for each orbifold, the orbifold fundamental group is isomorphic to the deck translation group.
Keywords: Groupoid presentation; Orbifold loop; Orbifold road; Orbifold fundamental group; Deck translation group
§1. Introduction
The original definition of orbifold was given by Satake [4], who viewed an orbifold X as a topological spaceXwith an additional structure on it. The structure of an orbifold is an atlas of local charts, in the way that each chart is given by an open subset ˜U ⊂Rn, a finite groupGacting smoothly on ˜Uand aG-equivariant mapπ: ˜U →X, which induces the embedding ˜U/G→X. Afterwards, Moerdijk [3] reformulate the notion of an orbifold using the language of groupoids, which allows us to deal with ineffective orbifolds, and brings important technical advantages. For instance, under the language of groupoids, we can discuss the orbifold vector bundles, cohomology, and homotopy groups etc.
For an orbifold X, perhaps the most important invariant is the orbifold fundamental groupπ1orb(X,x˜0),which was introduced by Thurston[5]for the study of 3-manifolds. Given an orbifold X presented by the groupoidG=(G0,G1), Moerdijk [2] constructs its classifying toposBG, and then defines the fundamental group of X asπ1(BG,x0). IfG0consists of simply connected open subsets, the orbifold fundamental groupπ1(BG,x0) can be identified with the vertex group atx0of the groupoidπ0(G0). In [1], Adem, Leida and Ruan consider the classifying spaceBG,and define thenthorbifold homotopy group of X based atx0∈Xto beπn(BG,x0). According to Moerdijk [2],BGandBGare weak homotopy equivalent. So we have

is a disjoint union of finite open sets inG1, and each of which is homeomorphic toVαunder both two mapssandt.

§2. Groupoid presentations of I and S1
In this section, we give the groupoid presentations of I andS1, which will be used to define the notions of orbifold road, orbifold loop, orbifold fundamental group and universal covering space in next sections. We will also give the compositions, inverses and refinements of the groupoid presentations.
LetI=[0,1] andS1={z ∈C||z|2=1}. We giveIandS1presentations of topological groupoid. Consider 0=u0<u1<...<un-1<un=1.ForI, we define the object space as the disjoint union


Finally, we define the refinement of groupoid presentations ofIandS1.
(1) For two groupoid presentations (I0,I1) and (I′0,I′1) ofI, ifI′0is a ordinary refinement ofI0, then the injectionφ0:I′0→I0induces the mapφ1:I′1→I1. We say (I′0,I′1) is a refinement of(I0,I1) with the embedding (φ0,φ1):(I′0,I′1)→(I0,I1).
(2) For two groupoid presentations (S0,S1) and (S′0,S′1) ofS1, ifS′0is a ordinary refinement ofS0, we say (S′0,S′1) is a refinement of (S0,S1) with (ψ0,ψ1):(S′0,S′1)→(S0,S1).
§3. Orbifold fundamental group
In this section, we define orbifold loops, and using which we reformulate the notion of orbifold fundamental group.
Definition 3.1.An orbifold road inX=(X,G)is defined as an groupoid homomorphism



commutes up to a natural transformationα:φ→f ◦ψ.


§4. Orbifold universal covering space and deck translation group
We first define the homopoty between orbifold roads.

And then we also define the homopoty relation⋍in G as follows,



Supposed0([r~x0,1~x0])=[r1,g1,···,rn,gn].Becausep0◦d0=p0, thent(gn)=˜x0. This means that [r1,g1,···,rn,gn]∈πorb1(G,˜x0).
We continue to showD([r1,g1,···,rn,gn])=(d0,d1). For any[l1,h1,···,lm,hm]∈˜G0,Because
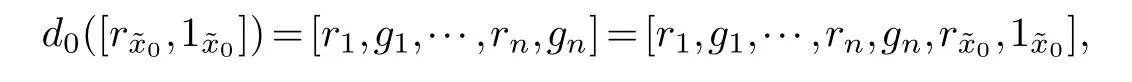

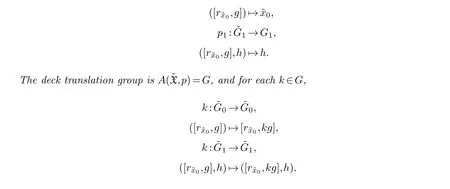
Example 4.2.Consider the teardrop WP(1,a), with the groupoid presentation G=(G0,G1)as the same as Example 3.2. For any[r1,g1,···,rn,gn],[l1,h1,···,lm,hm]∈˜G0, if[r1,g1,···,rn,gn]=[l1,h1,···,lm,hm], then t(gn)=t(hm).
On the other hand, if t(gn)=t(hm), according to Example 3.2,
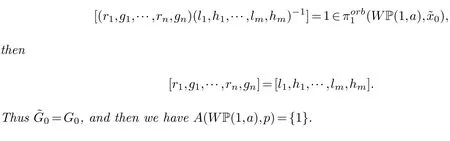
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Global Existence and Uniqueness of Periodic Waves for a Perturbed Combined Double-Dispersive Equation
- On the Factorization Numbers of a Class of Finite p-Groups
- Singular Integrals on Product Spaces with Mixed Norms
- Majority Coloring of r-Regular Digraph
- Asymptotic Property of Solutions in a 4th-Order Parabolic Model for Epitaxial Growth of Thin Film
- Majorization and Fekete-Szeg¨o Problems for Multivalent Meromorphic Functions Associated with the Mittag-Leffler Function
