Asymptotic Property of Solutions in a 4th-Order Parabolic Model for Epitaxial Growth of Thin Film

--

(College of Science, China University of Petroleum, Qingdao 266580, China)

Abstract: This paper deals with a homogeneous Neumann initial-boundary problem of a 4th-order parabolic equation modeling epitaxial growth of thin film. We determine the classification of initial energy on the existence of blow-up, global existence and extinction of solutions by using the potential well method and the auxiliary function method.Moreover, asymptotic estimates on global solution and extinction solution are studied,respectively.

Keywords: 4th-Order parabolic equation; Asymptotic estimate; Blow-up; Extinction;Initial energy

§1. Introduction

In the present paper, we study a continuum model for epitaxial growth of thin film, which is formulated as a 4th-order parabolic equation involving variable exponents,

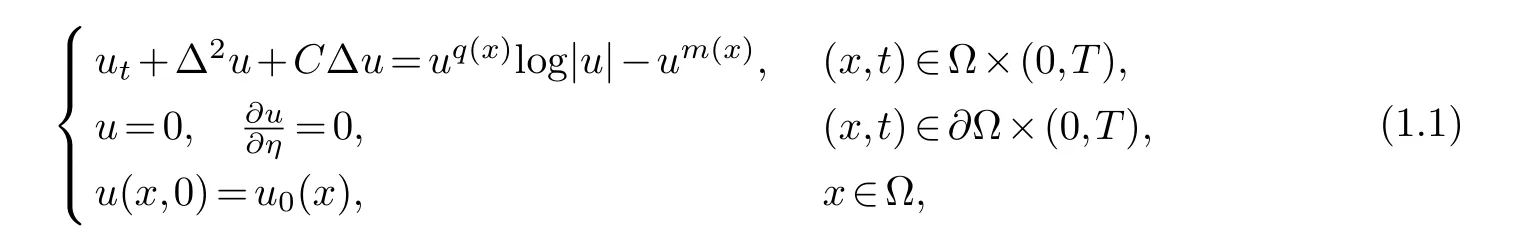
where Ω⊂Rn(n≥1) is a bounded domain with smooth boundary;T ≤∞is the maximal existence time of solutions;ηdenotes the unit outward normal vector on∂Ω; Initial datumu0∈H20(Ω). The process of building up a thin film layer on a substrate by chemical vapor deposition has now given risen to several descriptions and simulations by atomistic as well as by continuum models (see e.g., [5]). Particularly, Δ2udenote the capillarity-driven surface

CΔuis a diffusion term due to evaporation-condensation, where the positive constantCwill be determined later. For more information on background, the interested readers may refer to the works [9,13]. The equations involving variable exponents like (1.1) are the so called high-order parabolic equation with nonstandard growth conditions which have been rarely considered before(see [1]).

King, Stein and Winkler in [7] considered the initial-boundary problem of the equation

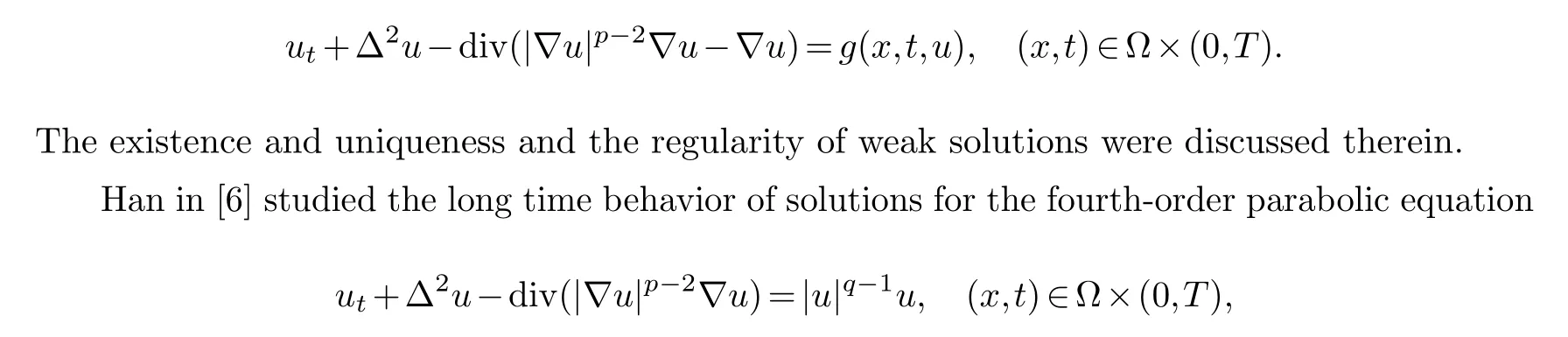
subject to homogeneous Dirichlet boundary conditions. The author gave a threshold result for the solutions to remain global or to blow up in finite time where initial energy is subcritical and critical, respectively. Moreover, the decay rate of weak solutions inL2-norm was obtained for global solutions. Some sufficient conditions for the existence of global and blow-up solutions were proved for the supercritical initial energy. For the more corresponding results, we referred the interested readers to the works [2,3,8,10,11,14].

Inspired by the work [6], we would give an optimal classification on the singularity of weak solutions to (1.1). The first difficulty needed to overcome is that the maximum principle and the comparison principle are invalid for the 4th-order parabolic problems. The second difficulty is caused by the variable exponents. Such as, self-similar transformation is failed; Most of the traditional embedding inequalities do not hold in the variable Sobolev spaces. For the subcritical and critical initial energy cases, we would combine the generalized Galerkin’s method with the improved potential well method to prove the existence of global weak solutions. In addition,combining the concavity arguments with the extended potential well method, we obtain the results of blow-up solutions under proper conditions on initial data. For the super critical initial energy, our idea comes from [4,12]. Moreover, we use the energy estimate and the auxiliary ordinary differential inequality to study the extinction and non-extinction of weak solutions.

This paper is arranged as follows. In the next section, we show the main results and show the classification of the initial energy by using Table 2.1 below. Sections 3, 4 and 5 will be devoted to the proof for the subcritical, critical and super critical cases, respectively.

§2. Main results

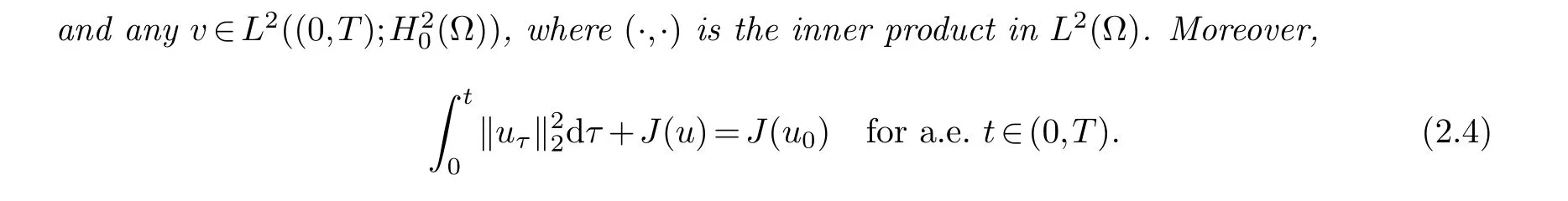
2.1. Subcritical initial energy J(u0)＜d

Theorem 2.1.Let(H), q-＞m+＞1and q(x)q′(x)＜4*+1be in force.

(i)If J(u0)＜d and I(u0)＞0, then problem (1.1) admits a global solution

2.2. Critical initial energy J(u0)=d

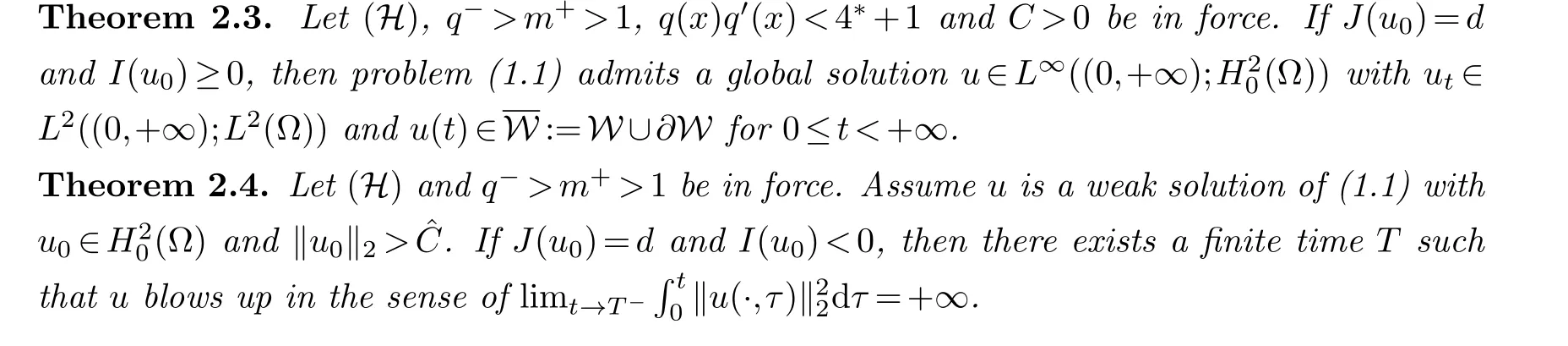
2.3. Super critical initial energy J(u0)＞d

Theorem 2.5.Let(H)and q-≥m+be in force and J(u0)＞d.

2.4. Extinction and non-extinction in finite time

2.5. Summarization

The main results of this paper could be summarized in Table 2.1. It could be checked thatI(u0)/=0 provided thatJ(u0)＜d. So the classification of initial data is optimal for the existence of blow-up or global solutions to (1.1).

Table 2.1 Classification of initial energy.

§3. Proof of Theorems 2.1–2.2

At first, we introduce seven lemmas as preliminary.

Lemma 3.1.The depth d of the potential well W is positive.

Next,we claimI(u)＜0 for allt∈[0,T). In fact,if it was false,it follows there would exist the first constantt0＞0 such thatI(u(t0))=0 andI(u)＜0 fort∈[0,t0). From Lemma 3.2 (ii), we have‖Δu(t)‖2＞r(1)＞0 fort∈[0,t0). By the continuity of‖Δu(t)‖2tot,we get‖Δu(t0)‖2≥r(1)＞0.Hence,u(t0)∈N. Then it follows from the definition ofdthatJ(u(t0))≥d, which contradicts to (2.4). Then from (3.12), one could getM′′(t)＞0 fort≥0. SinceM′(0)＞0, we haveM(t)≥M′(0)t. Therefore, for sufficiently larget, we have (q--1)C21λ1M(t)＞(q-+1)‖u0‖22.Consequently, there exists a suitably larget*such that for allt≥t*,

§5. Proof of Theorems 2.5–2.7

Lemma 5.1.Let(H)and q-≥m+hold. For any s＞d, we have0＜λs ≤Λs ＜+∞.

Acknowledgements

The authors would like to thank the Editors and the anonymous Reviewers for valuable and constructive suggestions improving the first version of this paper.