Majority Coloring of r-Regular Digraph

----

(1. School of Mathematical Sciences, University of Jinan, Jinan 250022, China; 2. School of Mathematics and Information Sciences, Weifang University, Weifang 261061, China)

Abstract: A majority k-coloring of a digraph D with k colors is an assignment c:V(D)→{1,2,···,k}, such that for every v ∈V(D), we have c(w)=c(v) for at most half of all out-neighbors w ∈N+(v). For a natural number k ≥2, amajority coloring of a digraph is a coloring of the vertices such that each vertex receives the same color as at most a proportion of its out-neighbours. Kreutzer, Oum, Seymour, van der Zypen and Wood proved that every digraph has a majority 4-coloring and conjectured that every digraph admits a majority 3-coloring. Gir～ao,Kittipassorn and Popielarz proved that every digraph has a-majority 2k-coloring and conjectured that every digraph admits a -majority (2k-1)-coloring. We showed that every r-regular digraph D with r ＞36ln(2n)

Keywords: Majority coloring; Regular digraph; -Majority coloring

§1. Introduction

We adopt standard graph theory notation and terminology. Digraphs considered in this paper are finite and simple(loopless,have no parallel edges,but are allowed to have digons). LetDbe a directed graph,for a digraphD=(V(D),A(D))and every vertexv ∈V(D). LetN(v)denote the neighborhood ofvinD, andN+(v) (N-(v)) denote the out-neighborhood (in-neighborhood) ofvinD,d+(v)(d-(v))is the size ofN+(v)(N-(v)), and is called outdegree(indegree)ofvinD.δ+(δ-) is minimum outdegree ofD(minimum indegree ofD). Δ+(Δ-) is maximum outdegree ofD(maximum indegree ofD). A digraphDisr-regular ifd+(v)=d-(v)=r, ∀v ∈V(D).

§2. Our results

A majority coloring of a digraph D with k colors is an assignmentc:V(D)→{1,2,···,k},such that for everyv ∈V(D),we havec(w)=c(v)for at most half of all out-neighborsw ∈N+(v).This concept was introduced recently by van der Zypen [1] in connection to neural networks,who showed that every digraph is majority 4-colorable. His team proved this result on the basis that every acyclic digraph is majority 2-colorable. And they proposed the following conjecture.Conjecture 1.[1] Every digraph is majority 3-coloring.

And they also gave the following result.

Theorem 2.1.[1] Every n-vertex digraph G with minimum outdegree δ+＞72log(3n)has a majority 3-coloring. Moreover, at most half the out-neighbours of each vertex receive the same color.

§3. Proof of our results

At first, we introducedBIN(n,p) is the sum ofnindependent random variables, each equal to 1 with probabilitypand 0 otherwise. The ChernoffBound [7] bounds the probability thatBIN(n,p) is far fromnp, its expected value. For any 0≤t≤np,

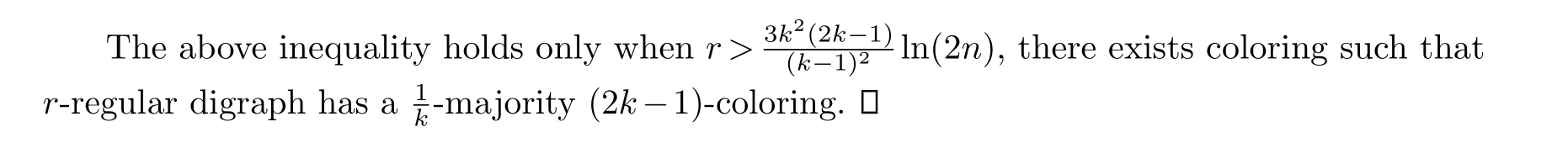
Acknowledgements

We would like to thank the referees for his(her) valuable comments and suggestions.