带精英集并行遗传算法的无人机干扰资源调度

邓 敏 伍志高 姚志强 陈永其

①(中国电子科技集团第36研究所通信信息控制和安全技术重点实验室 嘉兴 314000)

②(湘潭大学自动化与电子信息学院 湘潭 411105)

1 引言

近年来，无人机(Unmanned Aerial Vehicle,UAV)应用领域不断扩展，如何高效使用反无人机设备反制、干扰“黑飞”无人机，防护禁飞区域、防止重大事件现场信息泄露、打击利用无人机进行违法活动，成为行业热点，而通过电磁干扰使对方设备瘫痪是主要目标[1]。随着电磁环境复杂化、无人机行动方式协同化[2]，调度各种规模数量的干扰资源对无人机群进行协同干扰成为一种趋势。资源调度问题是一种NP(Nondeterministic Polynomially)问题[3]，至今没有最优的求解方法。已有研究集中在调度建模和求解算法两个方面。

在干扰资源调度建模与优化求解中，用最小的调度成本达到最大的干扰效益是主要目的。在模型构建方面，文献[4]将目标威胁等级、资源干扰样式以及目标雷达网的检测概率作为干扰效益，并对干扰数量、模式数量、被干扰数量和相同模式干扰机数量进行了限制。文献[5]以资源的协同规则构建了基于协同目标分配规则的模型，以反辐射杀伤收益为目标，并对是否攻击、单个无人机可攻击数量和目标可被攻击数量进行了约束。文献[6]根据干扰前后被拦截的雷达脉冲的幅度和数据速率变化，提出了一种从侦察和干扰系统的角度定量评估自我筛选干扰有效性和效果的方法。文献[7]从抑制功率、频率对准比、干扰覆盖空间和干扰模式分析收益，但仅对单个资源的可干扰数量和单个目标的可被干扰数量进行了限制。文献[8]以雷达网检测概率为评价指标，计算了单部雷达在多样式干扰下的检测概率，再映射到计算全网的受干扰影响程度。文献[9]将UAV的飞行距离作为效益，飞行时间作为成本，并对资源和目标的干扰数量以及被干扰数量、目标执行顺序、时间窗口、最大飞行路径和时间以及同时到达时间这几个方面进行约束。总体来说，现有单个干扰资源调度模型的评价指标类型较少，资源与目标的分配模式约束多为一对一或多对一，较少考虑完成任务数和资源使用情况的约束。而在一些应用中，只有当对方被干扰掉的无人机达到一定数量时，才能达到有效防护和反制目的，上述研究并未充分凸显出干扰无人机群的复杂环境。

根据资源调度优化问题的模型，已有研究提出了一些有效的求解算法。文献[10]提出了带动态交叉率与变异率的遗传算法，维持了群体的多样性，且避免了过早收敛。文献[11]提出了一种分层多代理优化算法，结合了多智能体优化算法和遗传算法(Genetic Algorithm, GA)，以提高资源利用率。文献[12]基于最佳动态反应设计了集中式迭代干扰策略选择算法，并基于学习自动机原理提出了分布式有限反馈干扰资源分配算法。文献[13]通过引入贪婪算法，增强了遗传算法的性能。文献[14]和文献[4]分别提出自适应蚁群算法、混合量子行为粒子群优化和自调整遗传算法，提高算法可靠性。文献[15]则利用人工免疫系统来求解问题。文献[16]聚焦于干扰抑制法的干扰能量比，将所提模型松弛为一个凸优化问题。文献[17]提出一种基于自举专家轨迹分层强化学习的干扰资源分配决策算法，解决跳频干扰决策难题。目前智能算法大多被用于求解小规模的资源调度问题，求解速度快于传统数学算法。文献[18]提出改进遗传算法，验证了大规模(如500:500)资源调度性能，但方案不能保证最少完成任务数等复杂情况。上述文献大多采用小规模、较少约束的干扰无人机群资源调度模型，对所用算法能达到的时效性和规模扩展后的适用性提及较少。而此类算法在中、大规模、多约束的情况下会有运行时间过长、局部收敛等问题，求解复杂度和耗时会增加，设计算法需要在时间和优化目标值之间折中。

并行计算因具有加速代码运行和避免算法过早收敛的特点，成为改进智能算法的一个方向[19]。并行进化算法有个体分布和维度分布两种类别。其中常用的个体分布有主-从模型、岛屿模型、细胞模型、混合模型以及池模型。基于并行进化模型的算法能够比非并行算法更快解决中、大规模的干扰资源调度问题，且能得到近似的优化目标值。

为了解决中、大规模复杂干扰资源调度问题，本文以干扰效益最大化、干扰成本最小化为目标，构建了资源调度优化模型，并提出一种基于主-从、岛屿混合模型的改进并行遗传算法。主要工作如下：(1)干扰效益从距离、频段、威胁等级以及功率压制比4个方面进行评价，干扰成本从资源占用，地理位置和被发现概率3个方面进行评价。(2)为灵活适应多无人机干扰环境，允许一个干扰资源最多能干扰K1个目标，一个目标最多可被分配K2个资源。(3)将资源被分配给某个目标与否建模为0-1规划，把某个目标被分配了干扰资源看作一个任务，提出最少完成任务数的约束，则需非线性约束来描述。与其他模型相比，所提模型的约束更复杂、对抗规模更大，在允许多对多的场景中保证优化调度方案能完成的最少任务数，并对闲置资源数量进行了限制。(4)针对中、大规模情况下，现有算法收敛过慢、耗时过长的问题，本文提出基于混合模型的改进并行遗传算法，并通过对比传统遗传算法、非支配排序遗传算法II[20]、修复遗传算法[18]、基于岛屿模型的并行遗传算法[21]和自适应模拟退火遗传禁忌搜索算法[22]，验证在迭代次数、耗时、目标值方面的性能。

2 干扰资源调度模型

2.1 干扰资源调度场景

假设在复杂通信场景中，多架无人机分布在海、陆、空3种地理位置中，由M个干扰资源和N个被干扰目标组成，每个干扰资源用序号i, i∈I={1,2,...,M}表 示，每个目标用序号j, j∈J={1,2,...,N}表示。具体干扰关系如图1所示。其中：单个干扰资源i最多可以干扰K1(1≤K1≤N)个目标；单个目标j最多可以被K2(1≤K2≤M)个干扰资源干扰；为了节约成本，这里限定未被调用的资源数 要 大 于 等 于K3M(0≤K3≤1)且 小 于 等 于K4M(0≤K4≤1) ；要 有K5N(0≤K5≤1)以 上 的目标被分配有干扰资源，即最少完成任务数为K5N。

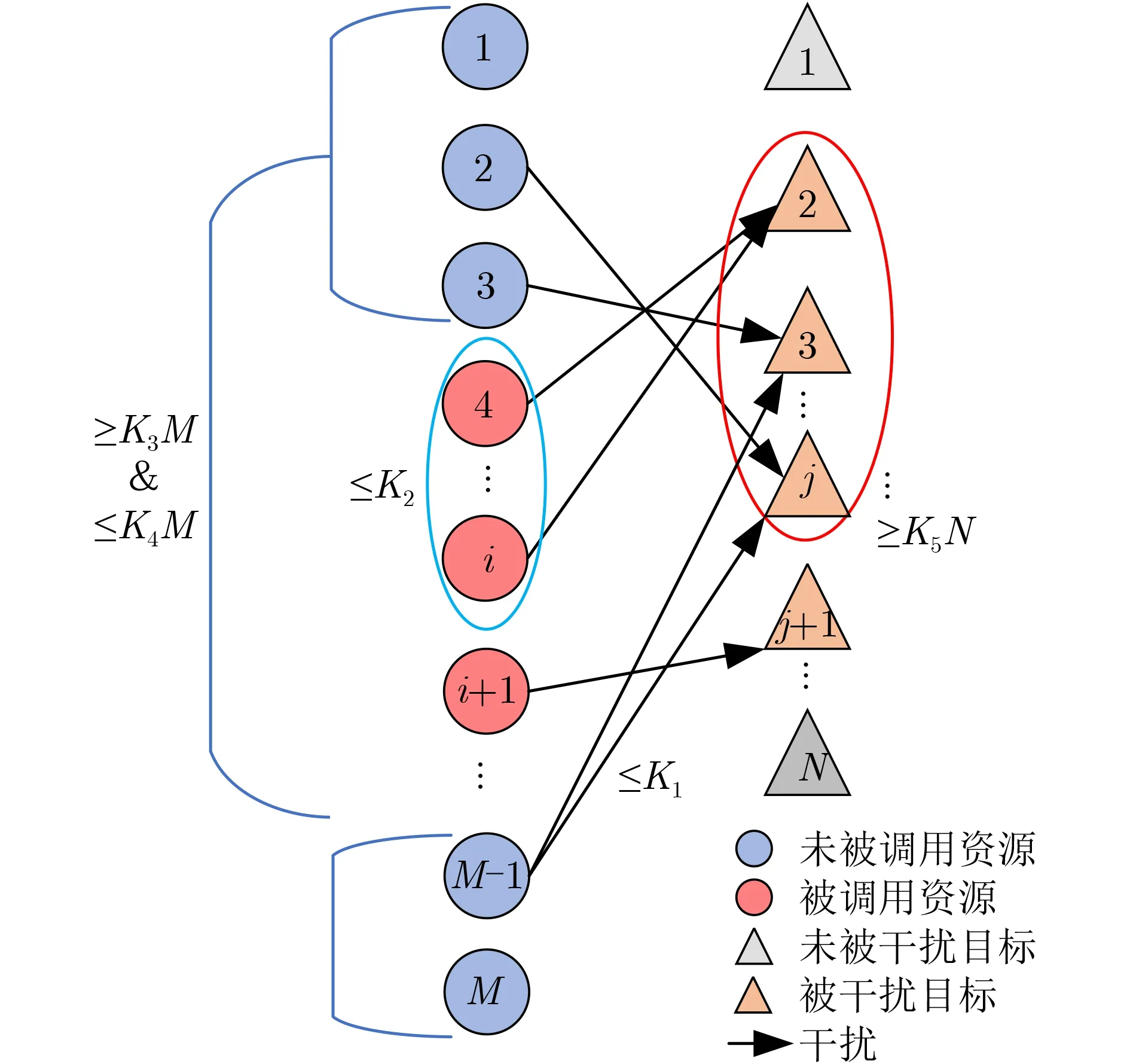
图1 干扰关系

假设目标的相关参数已通过侦察手段得到，则可通过分配干扰资源给合适的目标来得到干扰效益，同时支付相应的干扰成本。干扰效益和成本可根据双方参数计算相应的评估指标值来确定。其中，目标与干扰源通信的信道环境可根据实际场景设置经历信道衰落。在计算干扰效益和成本指标时，本文的接收功率和回波功率设置为空对空通信环境[23]中衰落后的功率。干扰效益和干扰成本则通过层次分析法(Analytic Hierarchy Process, AHP)进行加权整合，作为离散组合优化问题的目标函数，将双目标问题转化为单目标问题。2.2节将介绍干扰资源调度的评价指标，2.3节介绍干扰资源调度的数学模型。

2.2 干扰资源调度评价指标

2.2.1 干扰效益评价指标

(1) 干扰作用距离S1ij

2.3 数学模型

其中，K1, K2, K3, K4, K5的定义见2.1节场景部分，则K3M和K4M分别为未调用的资源数的最小值和最大值，以进一步约束调用资源的平均成本；K5N为被分配有干扰资源的最少目标数。

该资源调度优化模型的目标函数为非线性非凸的，约束条件中也含有非线性条件，难以用现有数学优化方法直接求解。

3 并行遗传模型求解算法

本文提出基于混合主-从、孤岛模型的并行遗传算法，来求解上述干扰资源调度问题。

3.1 基于主-从和岛屿模型的混合模型

主-从模式中，主处理器处理交叉变异和选择操作，随后把个体发送给从处理器。从处理器评估个体的适应度，且不需要与其他从处理器进行信息交流，从处理器之间相互独立。

岛屿模型与主-从模型不同之处在于将种群划分为不同子种群后，各子种群之间独立进化，只在固定的间隔与周围子种群进行随机的信息交流。岛屿模型的优点是节省时间，提高进化算法的全局收敛能力，但存在过早收敛的可能。

混合模型结构如图2所示，将种群划分为不同子种群，子种群独立进化一定次数后，将各自的最优个体上传至精英集。精英集将当前最优个体与全局最优个体进行比较后，更新全局最优个体，并通过信息交换将其发送给各子种群，继续进化。

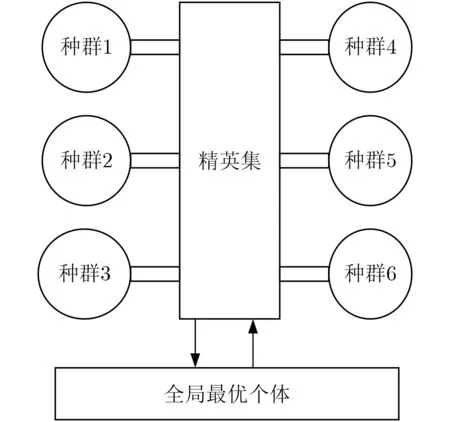
图2 混合主-从和岛屿模型结构

混合模型结合了主-从模型可以接收全局信息和岛屿模型提高收敛能力的特点，既增加了种群的多样性，又减少了过早收敛的可能。

3.2 基于混合模型的并行遗传算法

使用混合模型的关键是设置多个并行的子种群。并行的子种群在信息交流阶段之前各自并行进行遗传迭代，减少迭代耗时；在信息交流阶段产生精英集合G，保存全局最优个体的最优精英b0。S个子种群会在整个计算中进行多次信息交流。在信息交流阶段中，各子种群上传自己种群中的最优个体gk(k=1,2,...,S)到精英集合中，比较后将当前最优个体b1与全局最优个体b0比较，之后更新全局最优个体b0并将其发送回各子种群，进入下一阶段信息交流。干扰资源调度算法步骤如表1所示。

表1 基于混合模型的并行遗传算法(算法1)

遗传算法采取整数编码，每个个体表示为一个长度为干扰资源总数的向量，元素序号表示干扰资源的序号，向量中每个元素中的值为该干扰资源被分配的目标序号，若没有被分配目标则默认为0。

算法使用≥3个子种群并行进行遗传进化，随后输出各子种群的最优和最差个体，再通过信息交换，进行精英集更新等操作。

在算法运算中，通过多个子种群同时进行搜索，结合遗传交叉和变异操作，算法的搜索空间相对扩大，可以显著减少算法局部收敛的概率。同时，算法中的精英集收集和广播各子种群的最优个体，可以加快算法收敛速度。

4 仿真结果对比

假设干扰方有M个干扰资源(M默认为100)，干扰N个目标(N默认为50)，目标参数已通过侦察等手段获得。干扰约束条件同2.3节，K1=1，K2=2，K3=0.05，K4=0.5，K5=0.8。经多次遗传算法参数调整实验，并行遗传算法的交叉概率取0.8，变异概率取0.6，最大迭代次数为1500[11]，初始种群规模根据调度规模和子种群数量进行调整，在中等规模下初始种群规模为120。

本文将提出的基于混合模型的并行遗传算法，与遗传算法、修复遗传算法[18]、非支配排序遗传算法II[20]、基于岛屿模型的并行遗传算法[21]和自适应模拟退火遗传禁忌搜索算法[22]进行仿真比较。资源与目标的空间坐标随机变量服从均匀分布，包含海、陆、空地理属性，具体见2.2.2节干扰成本评价指标。

图3为单次中、大规模资源调度优化的目标函数值迭代趋势对比。其中，修复遗传算法在中间每次迭代中没有及时修正为满足多对一、最少完成任务数等多限制条件的可行解，虽具有最高的目标函数值，但迭代结束后的可行解目标函数值较低。为了便于对比，图中在修复遗传算法基础上，增加了每次迭代修复可行解的目标函数值统计。

由于本文算法通过3个子种群并行搜索，加大了可行解的搜索空间，减少了遗传算法局部收敛的可能性，而混合模型中精英集的引入，能够提高搜索速度。通过图3可以看出，本文算法的迭代收敛次数和收敛后目标函数值的性能。

图3 中、大规模资源调度优化目标函数值迭代趋势对比

表2为用改进的基于混合模型的并行遗传算法与其余5种算法进行不同规模下1500次迭代干扰资源调度优化的对比数据，取100次仿真的用时平均值与最终目标函数值平均值。由于非支配排序遗传算法II单次迭代运算方式与其余算法差异较大且耗时更长，其最大迭代次数仅取150。从表中可知提出的基于混合模型的并行遗传算法在指定迭代次数和计算至收敛两种情况都具有较短的计算时间和最高的目标函数值，且随着规模不断增大，优势越来越明显。

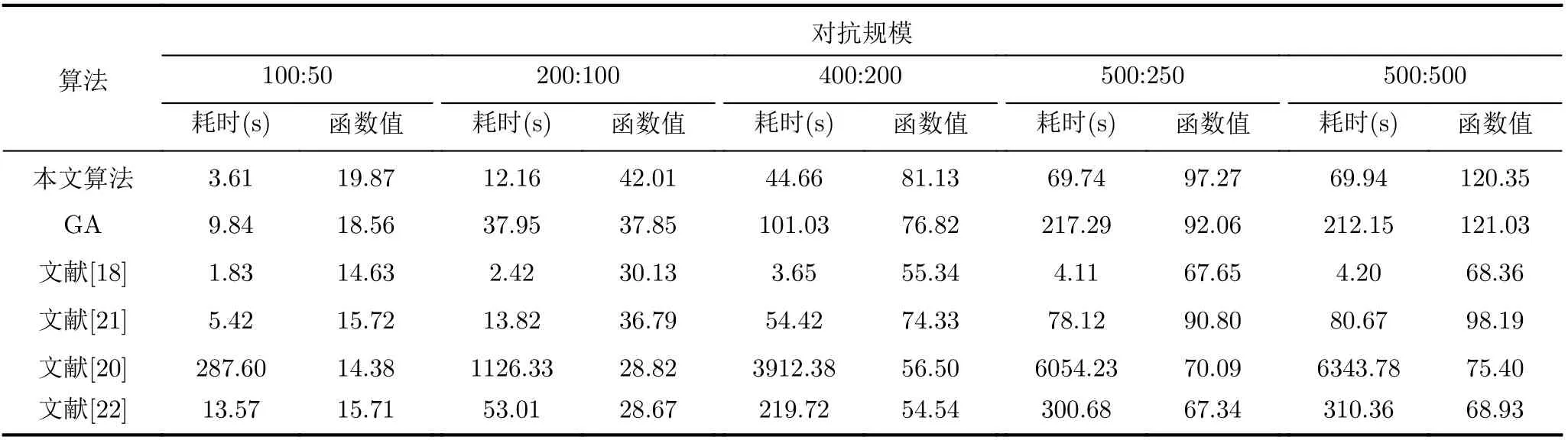
表2 迭代1500次所用时间/最终目标函数值对比(100次仿真平均值)

图4为判断收敛后停止计算的上述算法在100次仿真中用时平均值和最终目标函数值平均值对比数据，最大迭代次数取10000次，超出后停止计算。非支配排序遗传算法II由于上述原因取150次。时间方面，修复遗传算法虽然计算时间快，但没有在每次迭代后都修复不可行解，收敛之后再修复得到的满足约束条件的可行解的目标函数值并不高。

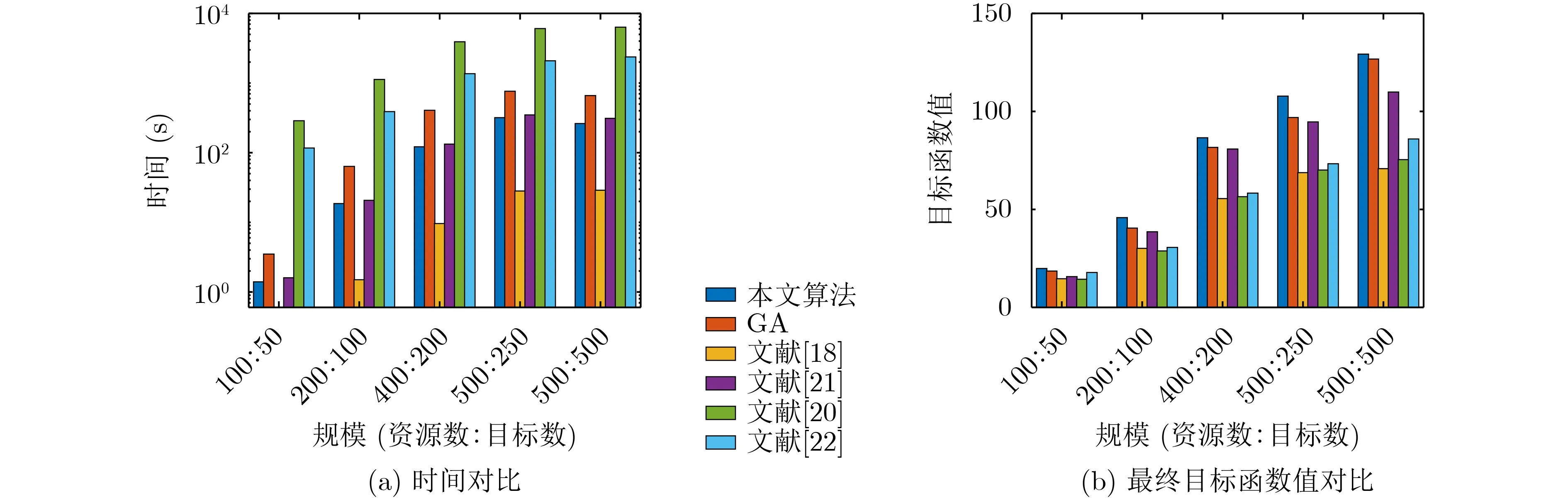
图4 算法收敛性能对比(100次仿真平均)

由于中、大规模资源调度问题中，启发式算法难以在多项式时间内取得最优解，为了对比各启发式算法取得最优解的稳定性，在小规模下，通过穷举法获得最优解，再将各启发式算法在同样的小规模情况下进行仿真实验。表3为在小规模(12:6)下，上述算法在100次仿真中达到最优的百分比统计，最优解的取值精度为1位小数。从表中可知，小规模的情况下基于混合模型的并行遗传算法达到最优的次数最多。

表3 在M=12, N=6规模下各算法在100次计算中取得最优解次数的百分比

为进一步研究所提算法在不同建模环境中的优化求解性能，本文在上述随机分布无人机干扰源、目标位置的基础上，考虑一种干扰源和目标群之间有一定空间界限的场景。图5为改变后的无人机干扰源和目标3维位置分布图。其中，最远目标离干扰源的距离为其信噪比达到最小可探测值时的探测距离。以中等规模资源调度问题为例，本文与5种对比算法得到的目标函数值迭代趋势如图6所示，可以看出本文算法仍能达到更优的目标函数值。当对抗场景中的资源或目标参数发生改变时，亦可将评估指标归一化，更新效益矩阵E后，使用本文算法优化调度方案。

图5 干扰资源与目标的空间位置

图6 中规模资源调度优化的目标函数值迭代趋势对比

5 结论

本文针对中、大规模干扰资源调度的时效和综合效益优化问题，构建了联合优化4种干扰效益和3种干扰成本的多目标优化模型，提出在允许多个干扰资源干扰单个目标、单个资源可同时干扰多个目标等条件下，保证最少完成任务数的约束，并提出基于混合模型的带精英集并行遗传算法来求解优化问题。

仿真结果表明，与基于岛屿模型的并行遗传算法、非支配排序遗传算法II和自适应模拟退火遗传禁忌搜索算法、修复遗传算法、经典遗传算法相比，所提算法在中、大规模下能够以较好稳定性在较短的时长内得到较高的目标函数值。

在其他领域的任务分配或资源调度应用中，可通过将分配、调度的对象处理成资源与目标对应关系，并采用合适的运算处理器，根据规模调整并行子种群数量后，将本文算法进行扩展应用，可提高时效性。后续研究将结合持续调度场景，根据不断变化的干扰场景，构建动态资源调度模型，引入新兴的侦干一体机，提出侦察干扰双层资源调度模型和算法，以适应各种规模资源调度优化。