道路土石方调配数学模型与方案精细度研究

刘广鑫，曾凡云，唐俊成

（中国电建集团中南勘测设计研究院有限公司，湖南 长沙 410014）

0 前 言

土石方调配是土木工程中的重要环节，尤其在水电工程、道路工程中土石方调配方案的优劣对工程的经济性产生了重要的作用。土石方调配问题主要针对工程项目在施工过程中产生的土石开挖、填筑量进行最优分配。过程中涉及土石料的利用率、各区域之间的运距、取弃土场的位置等一系列问题。

土石方最优调配的现有研究成果多针对于水电工程项目，道路工程方向研究较少，且多延续水电工程项目的做法，适用性不强。道路工程中的土石方调配由于其工程的线性特点，路线较长，土石方调配方案更为重要。同时，由于道路工程全线的土石分布情况较为复杂，对土石料的分类要求和利用要求更为严格，土石方的调配问题有其独特性。

国内外对土石方最优调配的研究侧重于水电工程的土石坝土方平衡问题，研究方法以线性规划建立数学模型为主。天津大学的胡程顺、钟登华等对土石坝的最优调配问题进行总结［1］，并提出了通用性较强的土石坝最优调配数学模型。申明亮等针对堆石坝施工中的料物分配做了深入研究［2］，并编写了调配软件［3］。郑霞忠等以实际项目为依托，研究建立了针对性较强的线性规划数学模型［4］，并在项目中进行了应用。曹生荣等从水电项目中的道路工程土石方调配问题切入，提出了数学模型和工程应用［5］。以上学者在研究过程中，针对土石坝的土方平衡均提出了数学模型，数学模型在总体一致的基础上，各有侧重。道路工程由于其特殊性，其土石方最优调配的线性规划数学模型也有其特殊性。

综合以上研究成果，道路工程中的土石方最优调配问题没有针对性强、适用性强的研究成果可以应用［6～10］，以上成果多源自水电工程项目，道路工程的特性不明显，其数学模型未能综合考虑道路工程中的土石分类、利用率等多种因素。研究成果多为书面形式，数学模型的求解部分未能提出重复利用的工具性成果，没有适用性较强的软件程序可以使用。

1 道路土石方调配数学模型

1.1 工程特点分析

为构建具有道路工程特点的土石方最优调配数学模型，首先针对道路工程土石方调配问题的特点进行分析。将道路工程土石方调配的特点转化为数学问题，考虑到数学模型中。

道路工程由于其线性的特点，在土石方调配的过程中，一般考虑的土石种类较多，会根据各种土石类别分别计算松方系数和土石利用率，除工程项目自身的填挖方量外，沿线布置的取土场、弃土场同样要考虑各类土石的松方系数和土石利用率。需首先将此类问题转化为数学问题。

本研究在建立土石方最优调配的数学模型时，部分摒弃了以往研究成果中的数学假定。例如，由于道路工程中在进行土石方调配之前取、弃土场的容量已经确定，所以摒弃掉以往研究成果中料场容量无限大的数学假定；道路工程中的土石料进行了详细的土石种类划分，确定了各类土石的土石松方系数和土石利用率，所以摒弃掉以往研究成果中关于料场可满足任意级配要求的数学假定；道路工程中要求整个项目满足填挖平衡，即所有的填缺区域需要填满，所有的挖余区域都要被使用或者弃置，所以摒弃掉以往研究结果中关于不考虑开挖料及中转料场的弃渣的部分。

综合道路工程土石方调配中的特点，结合道路工程中的土石方调配问题中各类土石的松方系数［11］、土石成分［12］、利用率等几个较为特殊的边界条件，建立了可应对各种情况的道路土石方调配数学模型。

1.2 建立数学模型

模拟一个完整的道路土石方调配过程：考虑路基设计方案中有m个挖方区域，其体积为W1～Wm；n个填方区域，其体积为T1～Tn；r个取土场，其可用体积为Q1～Qr；s个弃土场，其容量为D1～Ds（如图1所示）。在调配过程中考虑土石成分、松方系数等条件的挖方折减系数awij、填方折减系数atij。在上述边界条件下，已知土石调配的运距为cij，求解最优调配方案xij，以达到整个项目调配的总运距最小等优化目标。

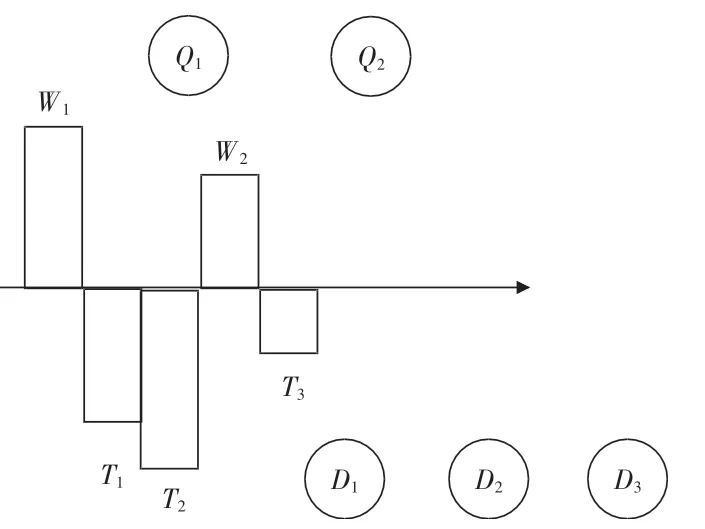
图1 土石方调配边界条件示意

这一问题可看成典型的产销平衡问题，适合利用线性规划的方法进行数学建模与求解，将此问题抽象为线性规划矩阵模型，如图2所示。

图2 土石方调配问题对应的线性规划矩阵示意

1.2.1 目标函数

本数学模型按照道路工程传统上运距最优的目标为例，目标函数如式（1）所示：

式中：Cij表示由第i个土石来源区域调配到第j个土石目标区域的运距；xij为第i个土石来源区域调配到第j个目标区域的土石总方量。

1.2.2 约束条件

根据道路工程土石方调配的要求可抽象出4个约束条件：为挖方约束、为填方约束、为取土场约束、为弃土场约束，如式（2）所示：

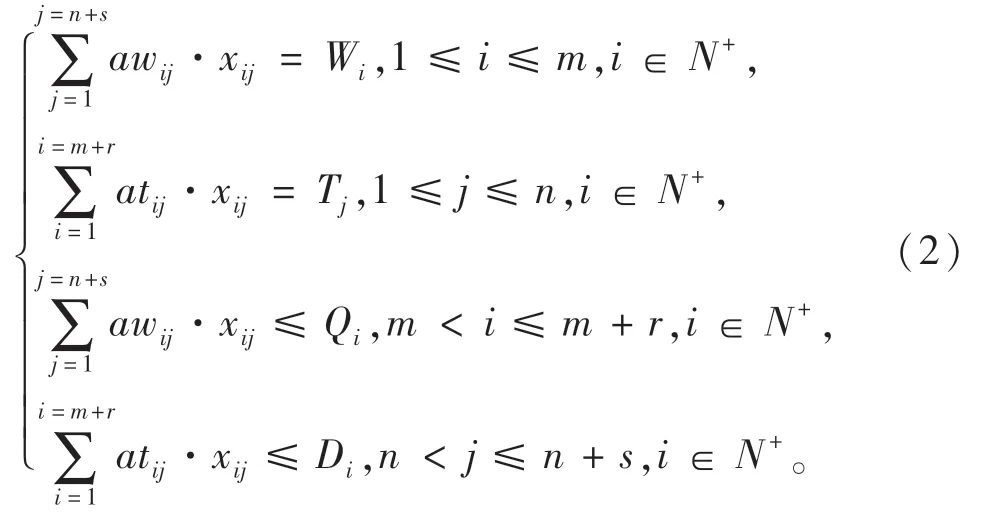
式中：aw、at表示土石体积修正系数；xij表示调配土石料的体积；Wi表示挖方区域土石料总体积；Tj表示填方区域所需的土石料总体积；Qi表示取土场的土石料总体积；Di表示弃土场的土石料容量的总体积。

1.2.3 软件设计

本研究同时编写了土石方自动调配软件，可以识别现有道路设计软件的土石方基础数据文件格式，软件核心算法采用的1.2中建立的数学模型，包含了数据前处理、求解、数据后处理3部分。

（1）数据前处理。根据道路工程项目信息，读取数学模型求解所需要的基础数据进行前处理，包括项目全线填挖区域的方量、各类土石的土石成分以及项目上已经确定的土石松方系数。

（2）求解。软件采用开源数学库glpk进行数学求解，通过求解器快速求解出方程组在可行域内的最优解，具体如下：

（3）数据后处理。根据数据前处理的运算过程解析出调配方案，将调配方案结存储到数据库，方便后期查看、出表等。

2 方案精细度优化

2.1 方案精细度分析

国内外现有的相关研究，几乎没有对土石方调配数学模型的最优解进行分析。本研究从实际项目出发，最终结果需要应用到实际工程中去，所以对数学模型求出的最优解进行了分析。

本节以某道路工程项目为例，采用本研究建立的数学模型进行最优解计算，进行分析。工程为某省道项目的一段，全长约4.8km，道路横断面采用公路二级标准设计。在数据前处理中，根据线性规划方程求得的最优解——二维数组xij绘制3D堆积条状图，如图3所示。i轴表示数学模型的下标i；j轴表示数学模型的下标j，xij表示土石方量，m3。由于全线范围内的解为474×478的数组，共有474个挖方区域Wi和478个填方区域Ti，数据量巨大。本节主要研究最优调配方案的实际项目可行性，注重最优调配方案的细节，所以图3仅截取其中的0～1.5km的结果进行局部分析。

根据图3所示，可以发现数学模型计算出的纯数学解具有明显的数学特点，即：碎片化。这种碎片化特点在图4的局部细节放大图中更易观察。

图3 自动调配方案3D堆积条状图（局部）

图4 局部细节放大示意

如图4所示，以0≤i≤15为例，每一处i区域的土石料被细碎的分散成0.1～1m3调配至多个j区域。这在数学角度是可以理解的，最优解的情况可以是离散的、碎片的。但从工程角度，这种最优解是不可取的，将某一挖方区域的土石方分成细散的几十个甚至上百个部分，分别调配到不同区域，这在人力物力调度角度是不现实的。

2.2 数学模型优化

为了利用本数学模型的最优解，同时解决最优解的离散性问题。本研究针对道路工程土石方调配的实际情况提出了方案精细度P的概念。

方案精细度P指实际项目中根据土石方调配使用的交通工具、人力等实际因素确定的调配方案xij精细程度。基于方案精细度P对本文建立的数学模型进行优化，采用整数规划。将计算所需的土方数据基于P整数化。

以2.1中的工程项目为例，首先根据项目实际情况确定方案精细度P（一般取项目使用运土车的容量，如10m3），对调配过程基于P进行优化处理，该处理仅对基础土石数据进行合并，未影响土石数据的精确性。采用glpk整数规划求解器进行求解后，得到与图3相同区域的优化后自动调配方案3D堆积条状图（局部），如图5所示。

由图5可见，优化后的调配方案不再有碎片化的缺点，调配方案的xij均为方案精细度P（本例为10m3）的整数倍，且调配方案更加整体化，可以直接应用于实际项目的土石方调配工作中，大大增加了最优调配方案的适用性。

图5 优化后自动调配方案3D堆积条状图（局部）

综合以上几点，证明方案精细度优化后的数学模型既可以快速地生成优于手动调配的最优调配方案，又可直接将调配方案应用于实际项目。

3 工程实例应用

为验证本数学模型的适用性，针对多个道路工程项目进行了传统的土石方手动调配，形成调配方案。同时采用优化后的数学模型，利用本研究编写的土石方自动调配软件进行自动调配，形成了自动调配方案。将手动调配方案和自动调配方案进行对比，对比结果见表1。

表1中6个道路工程项目道路包含了多种道路等级标准，项目均在可行性研究阶段确定了取弃土场的位置和容量。通过6个道路工程项目的手动调配与自动调配的方案对比结果得出结论：

表1 实际项目土石方调配方案对比

（1）本研究建立并优化的数学模型完美地适用于表中6个项目的土石方调配问题。

（2）相比于手动调配，自动调配无论在操作上还是用时上都大大地提高了效率，提高的效率在数量上与路线的长度呈正相关。

（3）本数学模型求得的最优解相比于传统手动调配方案更经济，降低了土石方调配的费用。

4 结 论

（1）结合道路工程特点，建立土石方最优调配数学模型。模型考虑了多个线性工程中特有的问题：土石分类、松方系数、土石利用率等。在道路工程领域适用性较高，可以处理现有工程中的各种实际问题。

（2）土石方自动调配软件是基于本研究建立的数学模型进行编写设计的，已经在多个道路工程实际项目中进行应用。通过与手动调配方案对比，大幅度减少了土石方调配的耗时，降低了土石方调配的成本。

（3）针对数学模型进行了方案精细度优化。未优化的原始方案是碎片化的，离散性较高，直接应用于道路工程项目的土石方调配中是不现实的。结合实际项目对方案精细性进行分析，提出了方案精细度P的概念，对原有数学模型进行了精细度优化。通过设置方案精细度P，提高了自动调配方案在实际项目中的适用性，使调配方案可直接应用于实际道路工程项目。