ABSOLUTE MONOTONICITY INVOLVING THE COMPLETE ELLIPTIC INTEGRALS OF THE FIRSTKIND WITH APPLICATIONS*

Zhenhang YANG (杨镇杭)

Engineering Research Center of Intelligent Computing for Complex Energy Systems of Ministry of Education，North China Electric Power University，Baoding 071003，China Zhejiang Society for Electric Power，Hangzhou 310014，China

E-mail:yzhkm@163.com

Jingfeng TIAN (田景峰)†

Department of Mathematics and Physics，North China Electric Power University，Baoding 071003，China

E-mail:tianjf@ncepu.edu.cn;tianjfhxm_ncepu@163.com

Abstract Let K (r) be the complete elliptic integrals of the first kind for r∈(0，1) and Using the recurrence method，we find the necessary and sufficient conditions for the functions (i=1，2，3) to be absolutely monotonic on (0，1).As applications，we establish some new bounds for the ratios and the product of two complete integrals of the first kind，including the double inequalities for r∈(0，1) and p≥13/32，where and θp=2Γ(3/4)4/π2-p.

Key words Complete elliptic integrals of the first kind;absolute monotonicity;hypergeometric series;recurrence method;inequality

1 Introduction

For real numbersa，bandc，with-N∪{0}，the Gaussian hypergeometric function is defined as

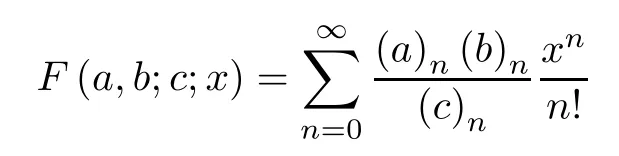
forx∈(-1，1)，where (a)ndenotes Pochhammer symbol defined by

forn∈N and (a)0=1 fora0;here(x＞0) is the gamma function (see[1，2]).In particular，the functionF(a，b;a+b;x) is called a zero-balanced hypergeometric function[3–5].

The hypergeometric functionF(a;b;c;x) has the simple differentiation formula

The behavior of the hypergeometric function close tox=1 is given by[6，Equations (15.1.20)，(15.3.3)，and (15.3.10)]

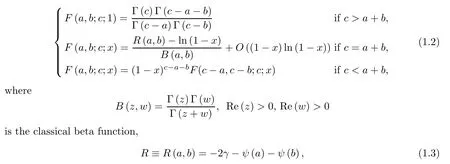
andψ(z)=Γ′(z)/Γ(z)，Re (z)＞0 is the psi function，andγis the Euler-Mascheroni constant.

The complete elliptic integrals K (r) and E (r) of the first and second kind are defined on (0，1) by

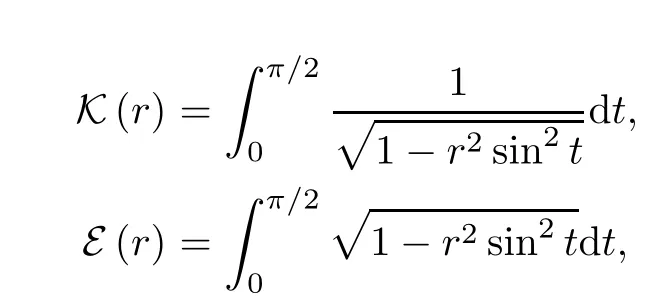
respectively (see[7]).They can also be expressed in terms of the Gaussian hypergeometric function as

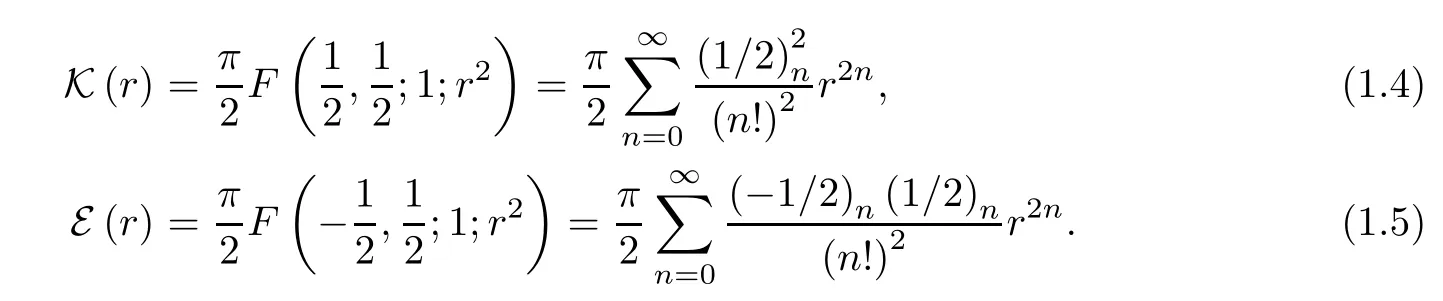
Using the asymptotic formula of (1.2)，we have

A functionfis called absolutely monotonic on the intervalIif it has nonnegative derivatives of all orders in the region;that is，

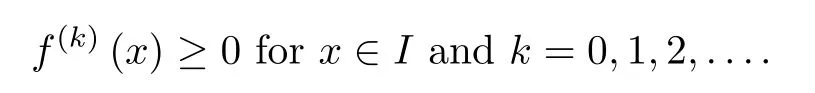
A functionfis called completely monotonic onIif it has a derivative of any order onIand satisfies that

(see[28]).For an even functionfdefined on (-a，a)(a＞0)，iffis absolutely monotonic on (0，a)，then it is completely monotonic on (-a，0)，and vice versa.

In 1990，Anderson，Vamanamurthy and Vuorinen[29，Theorem 2.2]showed that the function(r) is strictly decreasing from (0，1) onto (0，π/2);a generalization of this was presented in[30，Theorem 1.7].In[31]，the authors further proved that the functionr(r′)cK (r) is decreasing and concave ifc∈[1/2，2].Yang[32，Proposition]pointed out that the Macruain series of (r′)cK (r) has negative coefficients after a constant term ifc∈[1/2，2](instead of[0，1/2]，it is clearly a typo there)，without a strict proof.Recently，Richards[33，Lemma 2.3]claimed that this assertion also holds for the zero-balanced hypergeometric functions.

Motivated by these results，the first aim of this paper is to improve Proposition 1 in[32，Proposition]as Theorem 1.1，and then to give a strict proof by using the recurrence method.

Theorem 1.1Let

The function-is absolutely monotonic on (0，1) if and only if 1/4≤p≤1.

In 2019，Yang and Tian[34]conjectured that the functionfp(x) is log-concave on (0，1) if and only ifp≥7/32;this was recently proven in[35]by Wang et al.Inspired by this，the second aim of this paper is to study the absolute monotonicity of the function

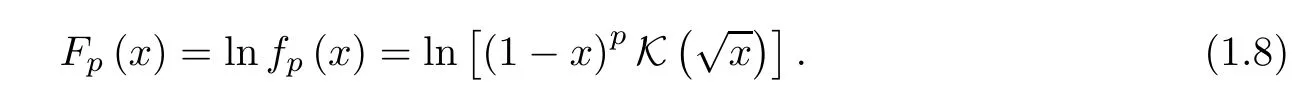
Our second result reads as follows:

Theorem 1.2Let the functionFp(x) be defined on (0，1) by (1.8).Then the following statements are true:

(i)Fp(x) is absolutely monotonic on (0，1) if and only ifp≤0;

(ii)-(x) is absolutely monotonic on (0，1) if and only ifp≥1/4;

(iii)-(x) is absolutely monotonic on (0，1) if and only ifp≥7/32;

(iv)-(x) is absolutely monotonic on (0，1) if and only ifp≥13/64.

For convenience，we useWnto denote the Wallis ratio:

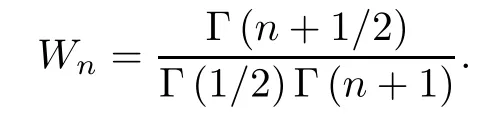
Clearly，Wnhas the following properties:

(i)Wnsatisfies the recurrence relation

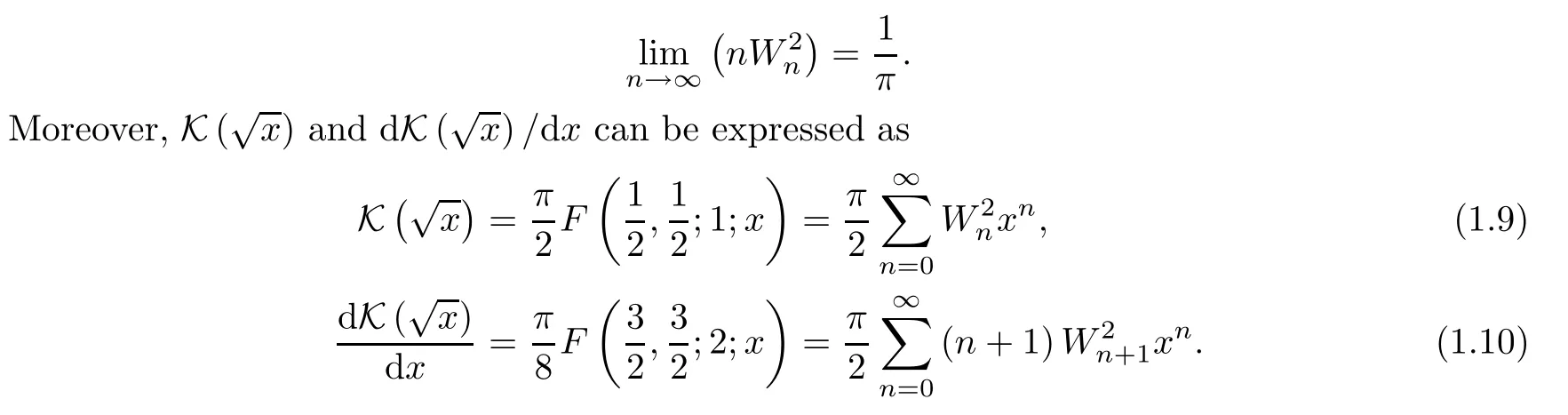
The rest of this paper is organized as follows:in Section 2，we prove Theorem 1.1 by using the recurrence formula given in[32，Lemma 2].In Section 3，we prove Theorem 1.2 by the recurrence method.As applications，we find，in Section 4，some new properties of ratios of two complete elliptic integrals of the first kind;this improves upon some known results.

2 Proof of Theorem 1

The following lemma comes from[32，Lemma 2]by replacing (r，p) by

Lemma 2.1([32，Lemma 2]) Forp∈R，the functionhas the power series representation

satisfying the recurrence relationa0=1，a1=1/4-pand

Before stating and proving the next lemma，we recall a class of special polynomials and their sign rule.A polynomial

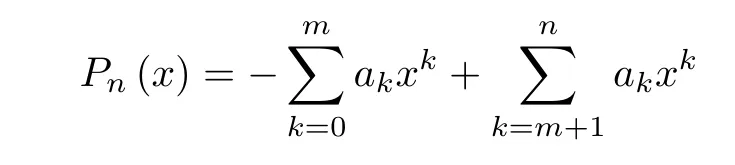
is called an negative-positive-type (NP-type) polynomial ifak≥0 for 0≤k≤nandCorrespondingly，-Pn(x) is called a positive-negative-type (PN-type) polynomial (see[36]).According to the sign rule for the NP-type polynomial (see[37，Lemma 2.2]，[38，Lemma 4])，there is a uniquex0＞0 such thatPn(x)＜0 forx∈(0，x0) andPn(x)＞0 forx∈(x0，∞).Consequently，for givenx1＞0，ifPn(x1)＞0，thenPn(x)＞0 for allx∈(x1，∞)，and ifPn(x1)＜0，thenPn(x)＜0 for allx∈(0，x1).

Lemma 2.2Letan=an(p) be defined on[1/4，1]by (2.2).Then the recurrence relation (2.2) can be written as

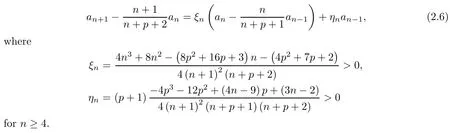
ProofAn elementary transformation yields

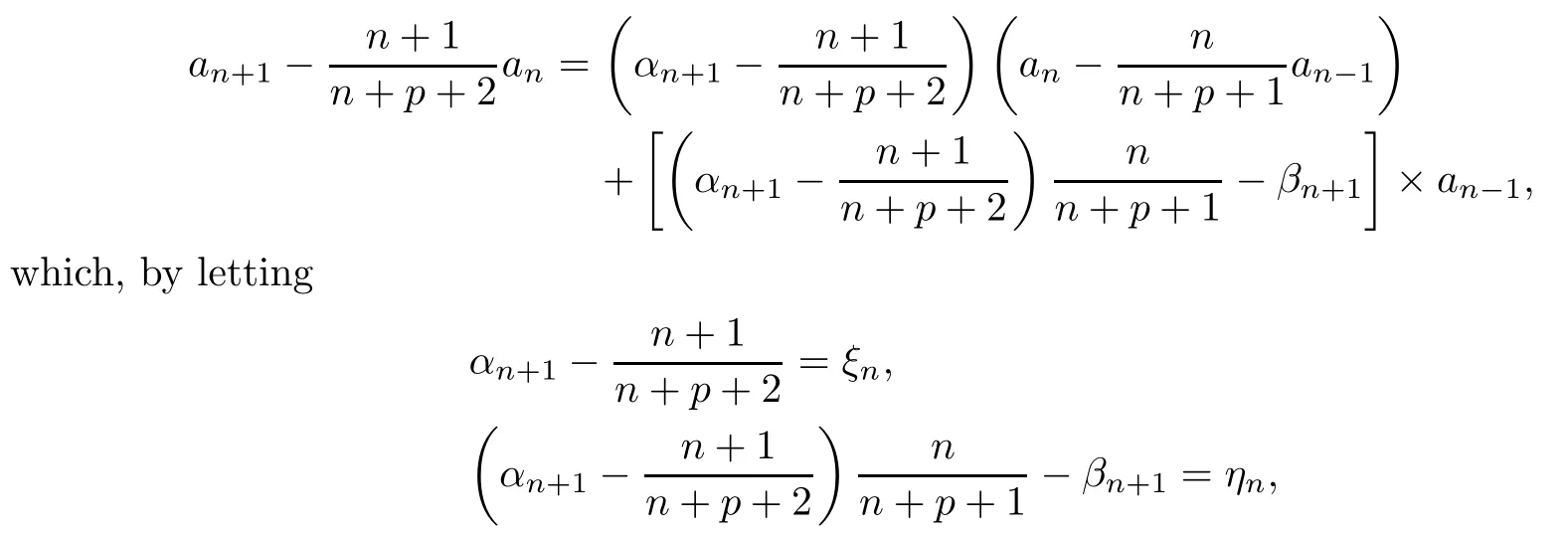
gives (2.6).It remains to check thatξn，ηn＞0 forn≥4.Since 1/4≤p≤1，the numerator of the expression ofξnis greater than

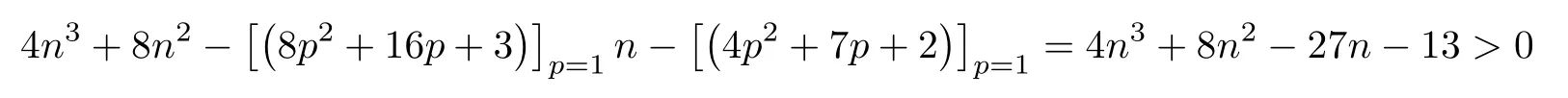
forn≥4.The numerator of the expression ofηn，denoted byln(p)，is greater than

Clearly，l4(p) is a PN-type polynomial，which is positive forp∈[0，1]，due to the fact thatl4(1)=1＞0.This completes the proof. □

We now give the proof of Theorem 1.1 by the recurrence method.

Proof of Theorem 1.1 Necessity.It is easy to see that the first necessary condition isa1≤0;that is，p≥1/4.To obtain the second condition，that isp≤1，we consider the sign of(x) asx→1.It is standard that

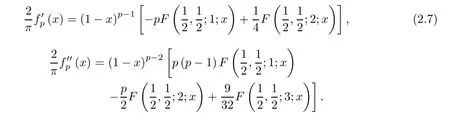
Since(x)＜0 forx∈(0，1)，we deduce that

which implies that 0≤p≤1.

Sufficiency.Suppose that 1/4≤p≤1.A straightforward computation gives that

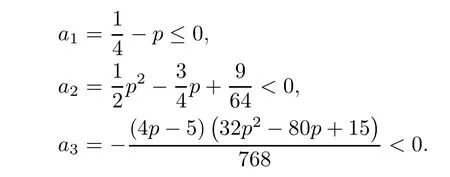
We show，by contradiction，thatan≤0 for alln≥1.Assume that there exists a positive term in the sequence{an}n≥1.Then all terms are positive after that.Let the first positive term bean0(n0≥4);that is，an≤0 for 1≤n≤n0-1 andan0＞0.We now provean＞0 forn≥n0by induction.We first show thatan0+1＞0 and

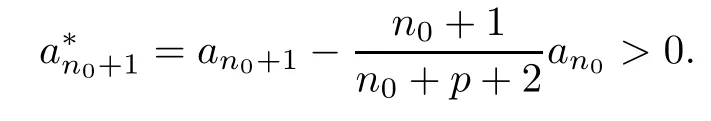
Due toan0＞0，an0-1≤0 andαn0+1，βn0+1，ξn0＞0 forn0≥4，and by the recurrence relation (2.3)，we obtain that

Assume thatan＞0 forn0+1≤n≤m.We now prove thatan+1＞0.Combining the relation (2.6) withξk，ηk＞0 fork≥4 andak-1＞0 forn0+1≤k≤nyields that

forn0+1≤n≤m.Thus，an＞0 for alln≥n0.It then follows that

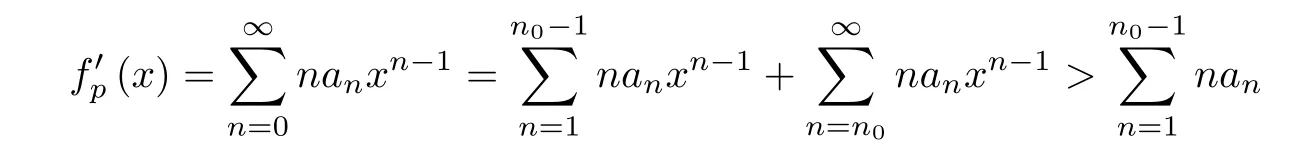
forx∈(0，1).On the other hand，from (2.7)，we find thatThis yields a contradiction.Consequently，there is no positive term in the sequence{an}n≥1;that is，an≤0 for alln≥1.This completes the proof. □

3 Proof of Theorem 1.2

To prove Theorem 1.2，we first give the power series representation of ln

Lemma 3.1We have

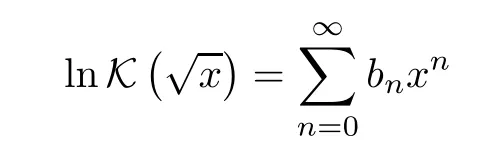
withb0=ln (π/2)，b1=1/4 and forn≥1，

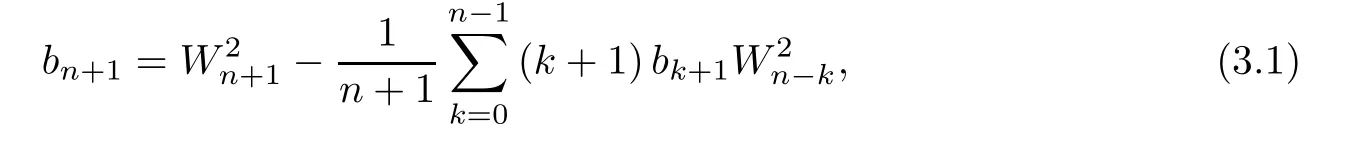
or，equivalently，

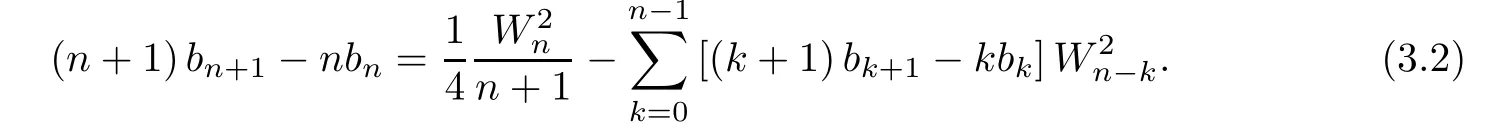
ProofWe have

Lettingx=0 givesb0=ln (π/2).Differentiation yields that

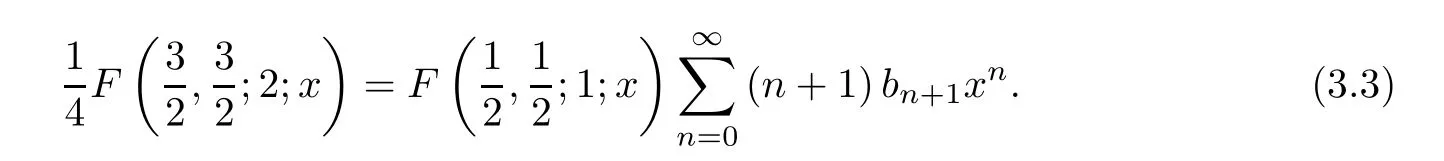
Using the Cauchy product and comparing the coefficients ofxngives

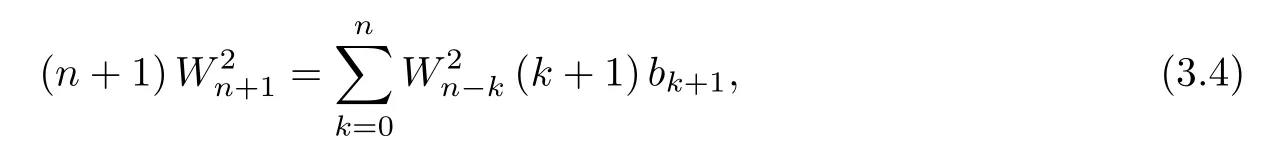
which implies (3.1) withb1=1/4.

Applying the third formula of (1.2) to (3.3)，we have that

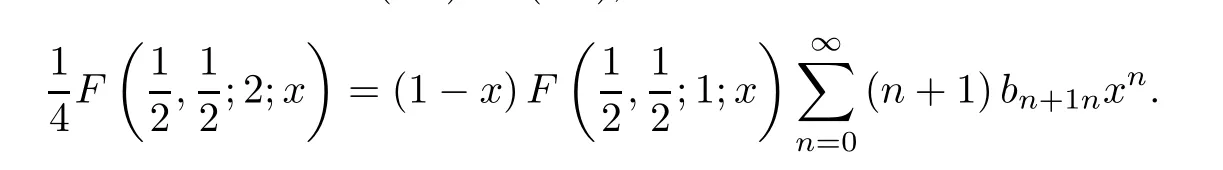
Using the Cauchy product and comparing the coefficients ofxnagain gives

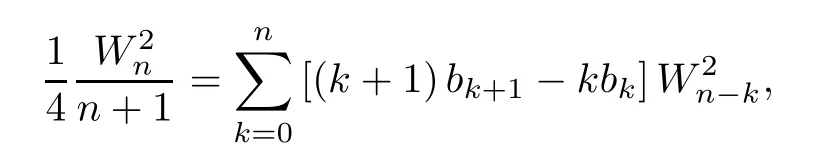
which implies (3.2)，thereby completing the proof. □

For later use，we list the values ofbnforn=2，3，4，5 by using recurrence formula (3.1):

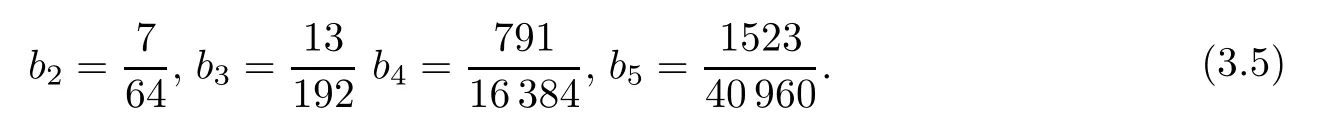
The following lemma reveals the positivity and monotonicity of the sequence{nbn}n≥1:

Lemma 3.2Letbnbe defined by (3.1).Then，(i)bn＞0 for alln≥0;(ii) the sequence{nbn}n≥1is decreasing with

Proof(i) By the recurrence relation (3.1)，we have that

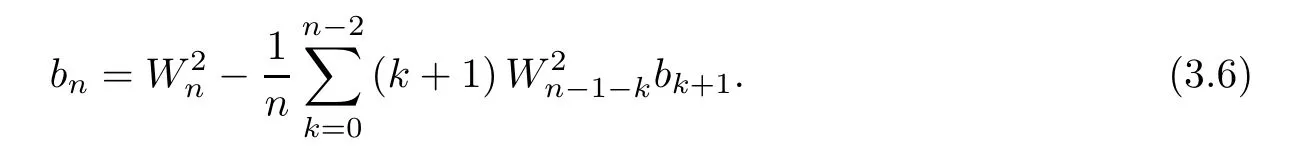
Eliminatingfrom relations (3.1) and (3.6) yields that

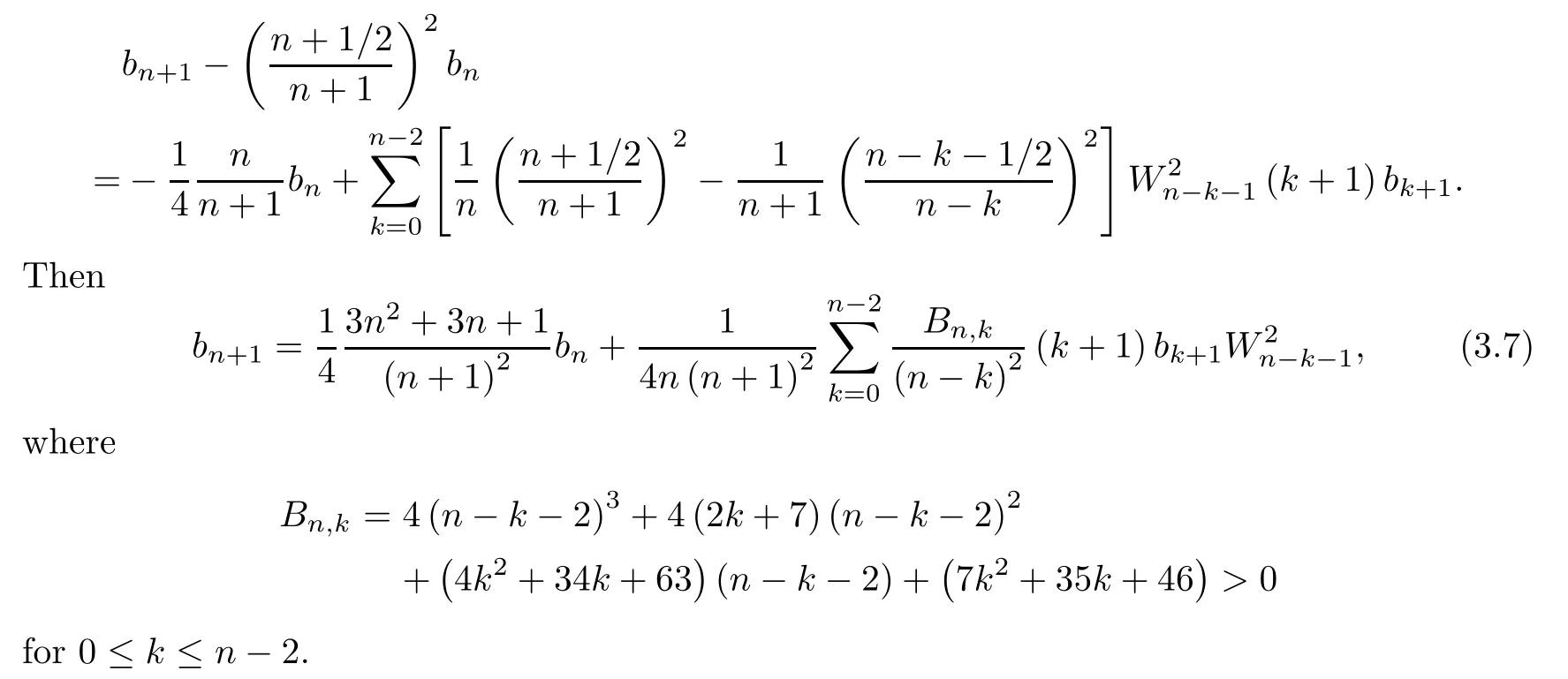
It is known thatb0=ln (π/2)＞0，b1=1/4＞0，and an easy verification yields thatb2=7/64＞0，b3=13/192＞0.Suppose thatbn＞0 for 1≤n≤m.Then，by (3.7)，we get at once thatbm+1＞0.By induction，the first assertion follows.

(ii) It suffices to prove thatb′n:=(n+1)bn+1-nbn＜0 forn≥1.To this end，we use the recurrence relation (3.2) to get that

Eliminatingfrom the above two relations，we get that

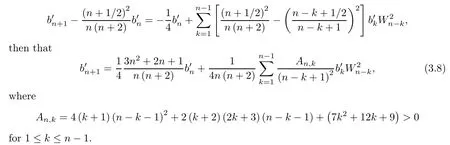
An easy verification yields that=-1/32＜0，and that=-1/64＜0.Suppose that0 for 1≤n≤m.Employing the inductive assumption to relation (3.8)，we immediately get thatBy induction，we arrive at0 for alln≥1.

it follows that 1/π≥ε×∞，which is，evidently，a contradiction. Thus there must bewhich completes the proof. □

With the aid of Lemmas 3.1 and 3.2，we are able to prove Theorem 1.2.

Proof of Theorem 1.2WriteFp(x) in the form of a power series:

It follows from Lemma 3.2 thatFp(x) is absolutely monotonic on (0，1) if and only ifp≤.Similarly，(x) is absolutely monotonic on (0，1) if and only if

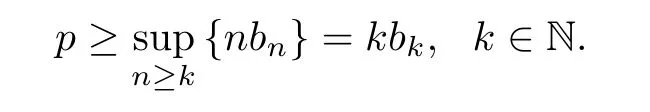
Then，due to the fact thatb1=1/4，b2=7/64 andb3=13/192，the second，third and fourth assertions follow，thereby completing the proof. □

4 Applications

As applications of our results，we will establish in this section some new properties of ratios and the product of two complete elliptic integrals of the first kind.

4.1 Monotonicity and inequalities for the ratio K (r)/K ()

In 1992，Anderson，Vamanamurthy and Vuorinenet[31，Theorem 3.11]proved that the inequalities

Recently，Alzer and Richards proved that the double inequality

is valid forr∈(0，1)，with the best constantsα=0 andβ=1/2.In this subsection，we will present several improvements to these above mentioned results.

Proposition 4.1Ifp≥1/4，then the function

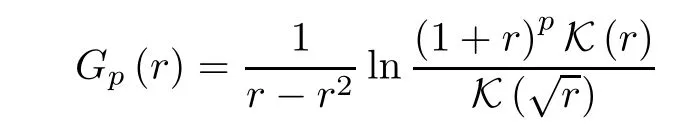
is absolutely monotonic on (0，1).Therefore，the inequalities

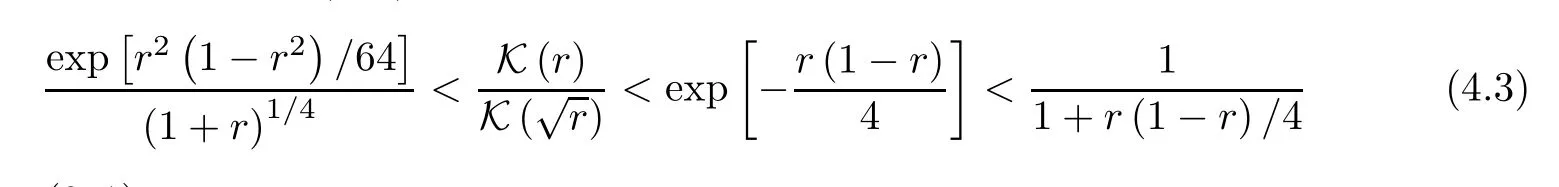
hold forr∈(0，1).

ProofUsing power series expansion (3.9)，we have that

This shows that-G0(r) is absolutely monotonic on (0，1).

The first inequality in (4.3) follows from

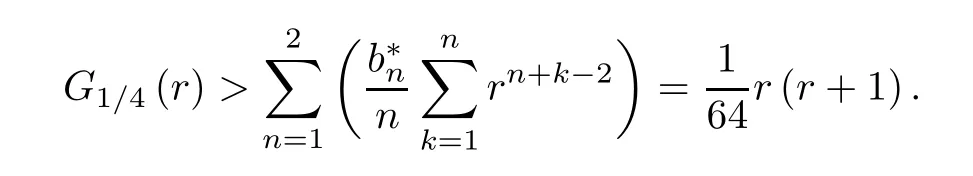
The second follows from-G0(r)＞b1=1/4，and the third holds due to a elementary inequalitye-x＜1/(1+x) forx＞-1.The required proof is completed. □

Remark 4.2We claim that our inequalities (4.3) are better than (4.1).First，our lower bound in (4.3) is clearly better than that in (4.1).Second，the inequalities

are obviously valid forr∈(0，1).Third，the inequality

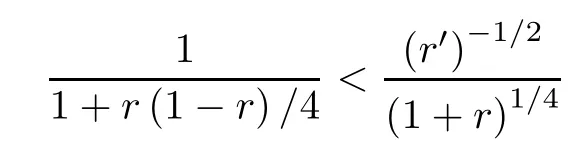
holds forr∈(0，1)，due to

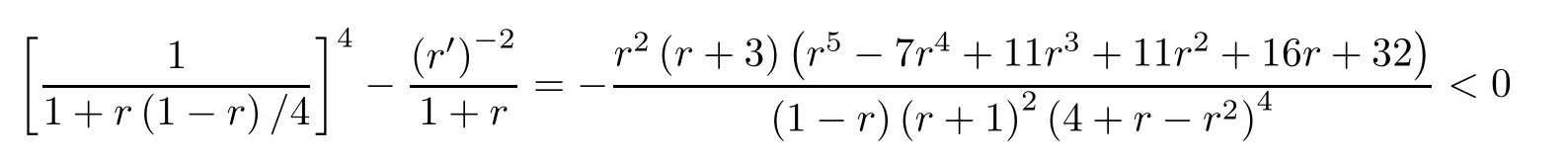
forr∈(0，1).Therefore，our upper bound in (4.3) is also superior to that in (4.1).

Proposition 4.3Letp≥13/64.The function

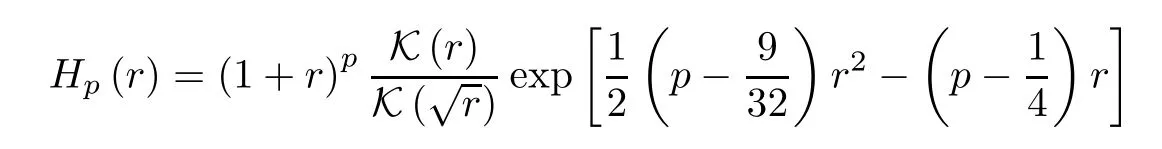
is strictly increasing from (0，1) onto (1，αp)，where

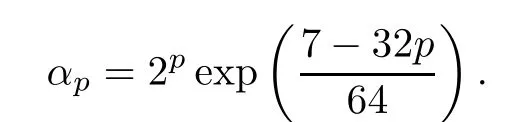
Consequently，it holds that

forr∈(0，1)，where

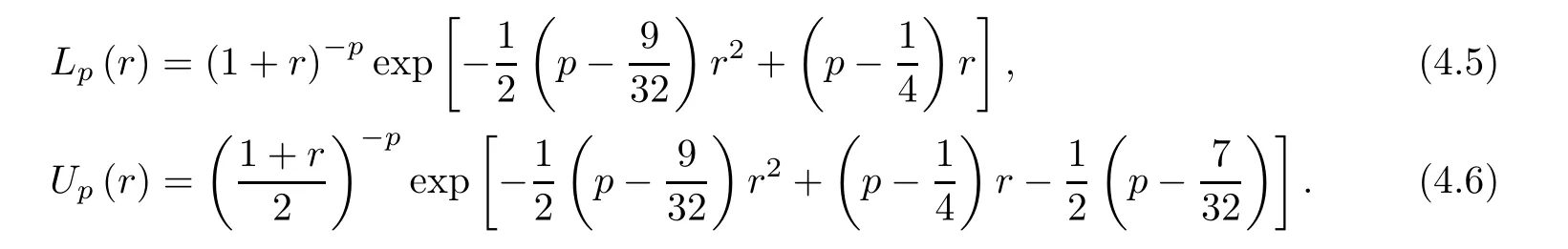
The lower and upper bounds in (4.4) are sharp.

ProofFrom power series expansion (3.9) we have that

Since，in view of Lemma 3.2 andthe sequenceis strictly increasing forn≥1，we have that

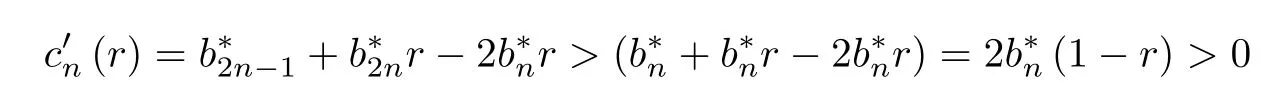
forn≥3.Also，it is clear that=p-7/32≥0，and if 13/64≤p＜7/32，thenhence，

We thus arrive at[lnHp(r)]′＞0 forr∈(0，1).The desired double inequality follows from the monotonicity ofHp(r) on (0，1)，which completes the proof. □

Remark 4.4We claim that the functionsLp(r) andUp(r)，defined by (4.5) and (4.6)，are decreasing and increasing，respectively，on R.In fact，differentiation yields that

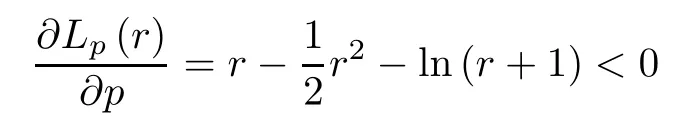
forr∈(0，1)，where the inequality holds due to the fact that

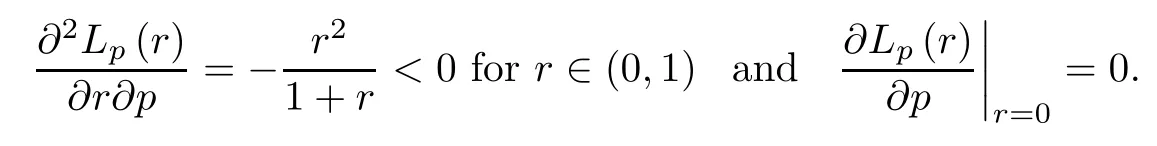
Similarly，we can prove that

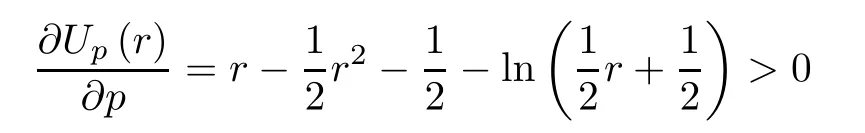
forr∈(0，1).Takingp=13/64，7/32，1/4in (4.4)，we obtain forr∈(0，1) a chain of inequalities:

Corollary 4.5LetLp(r) andUp(r) be defined by (4.5) and (4.6)，respectively.The inequalities

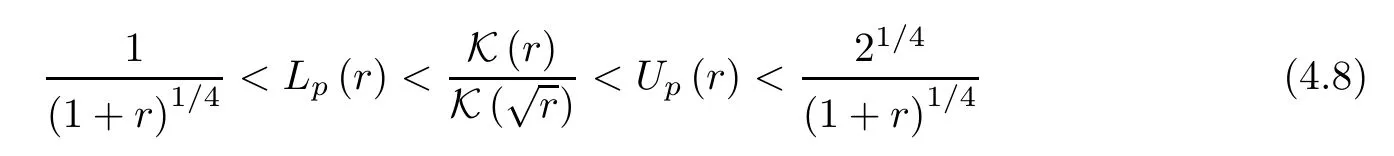
hold forr∈(0，1) if and only if 13/64≤p≤5/16.

Proof Necessity.From the proof of Proposition 4.3，we see that

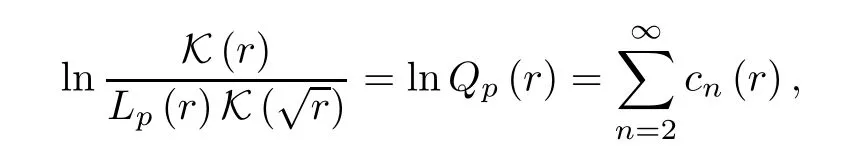
wherecn(r) is given in (4.7).Then the necessary conditions for inequalities (4.8) to hold forr∈(0，1) follow from the limit relations

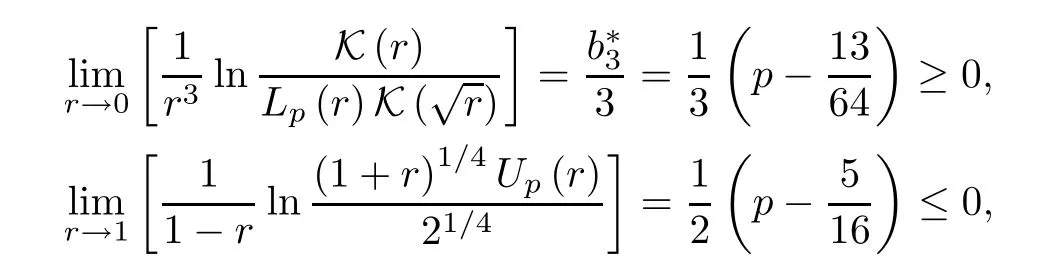
which implies that 13/64≤p≤5/16.

Sufficiency.The second and third inequalities of (4.8) follow from Proposition 4.3.Due to the monotonicity ofLp(r) andUp(r) with respect top(shown in Remark 4.4)，it suffices to show the inequalities

forr∈(0，1).Differentiation yields that

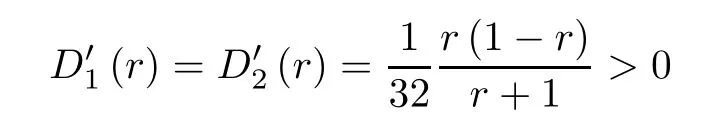
forr∈(0，1).This，together withD1(0)=D2(1)=0，gives thatD1(r)＞0 andD2(r)＜0 forr∈(0，1)，which proves the sufficiency.Thus the proof is completed. □

Remark 4.6By Proposition 4.3 and the proof of the above corollary，both of the functions lnQ5/16(r) andD1(r) are increasing on (0，1);so is

This gives a strict proof of Conjecture 3.1(2) in[31].

Finally，we give a refinement of inequalities (4.2).

Proposition 4.7The inequalities

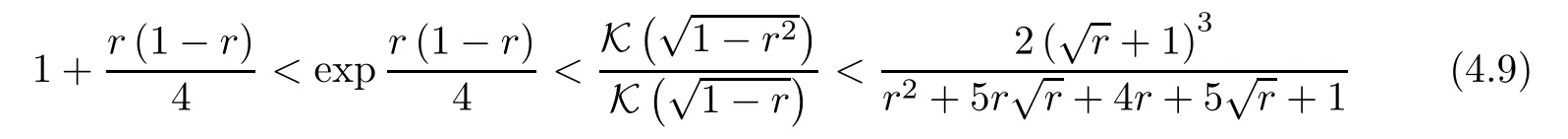
hold forr∈(0，1).

ProofUsing a power series expansion gives

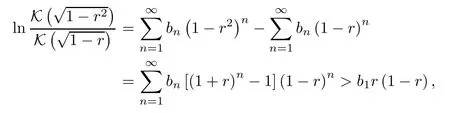
where，by Lemma 3.2，the inequality holds due tobn＞0 forn≥1.This implies that the second inequality in (4.9) holds forr∈(0，1).The first inequality is clearly valid.Applying the identity

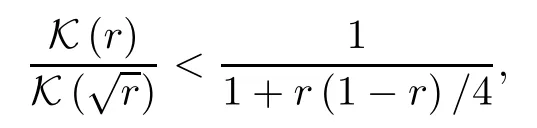
established in (4.3)，we arrive at

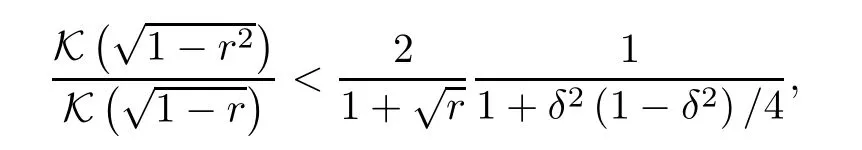
which is the third inequality in (4.9).This completes the proof. □

Remark 4.8It is easy to check that the inequalities in (4.9) are better than (4.2).

4.2 Absolutely monotonic and completely monotonic involving the ratio K (r′)/K (r)

The special function

forr∈(0，1) is called a modulus of the Grtzsch extreme ring，and it is indispensable in the study of quasiconformal distortion[42，43].

From Theorem 1.2，we see that the function(x)＜0 ifp≥13/64 and(x)＞0 ifp≤0.Using Hermite-Hadamard inequality，we have that

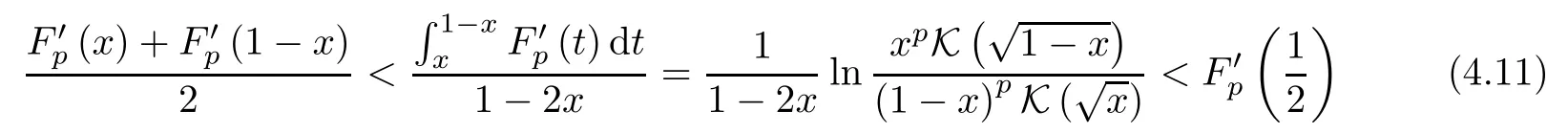
forx∈(0，1) withx1/2 andp≥13/64，which is reversed ifp≤0.By the derivative formulas

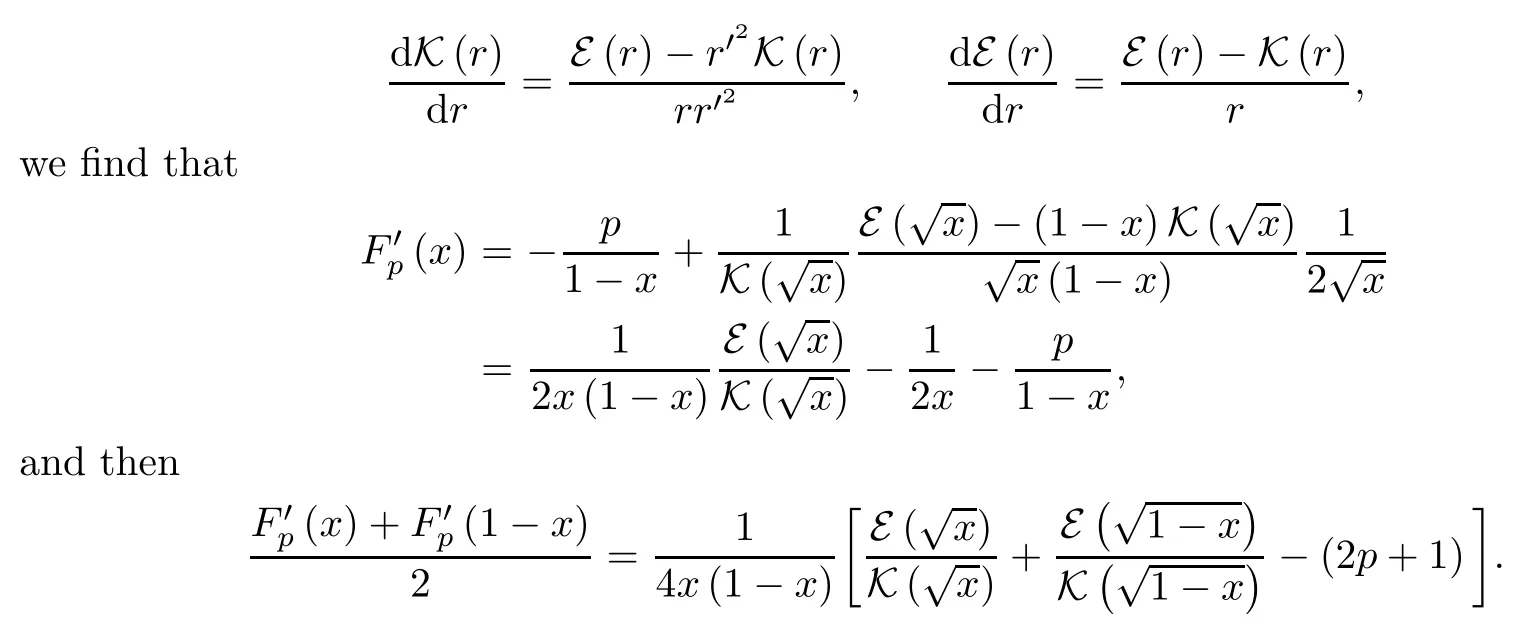
Also，it is known that

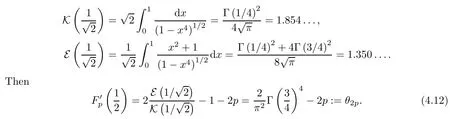
Replacing (x，2p) by（r2，p）in the double inequality (4.11)，we obtain

Proposition 4.9Ifp≥13/32=0.406...，then the double inequality

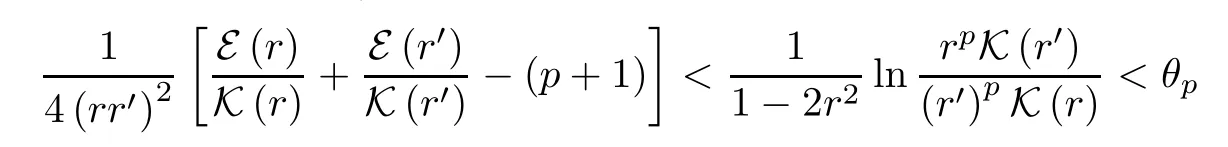
holds forr∈(0，1) withwhereθpis given by (4.12).This is reversed ifp≤0.

From the above proposition，we immediately get

Corollary 4.10Letμ(r) be defined by (4.10).Ifp≥13/32 andq≤0，then the double inequalities

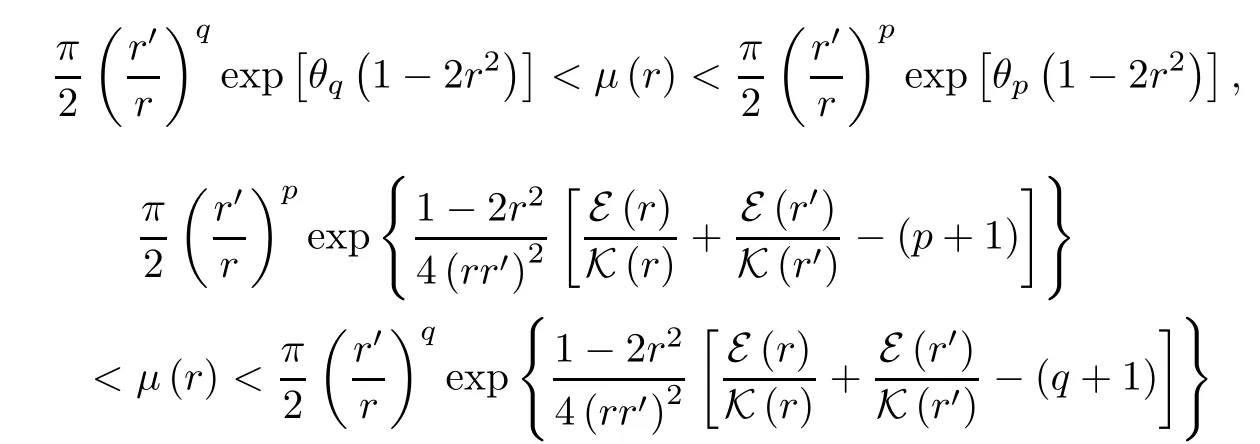
hold forr.They are reversed forr

Furthermore，we have the following interesting conclusion:

Proposition 4.11Ifp≥13/64，then the function

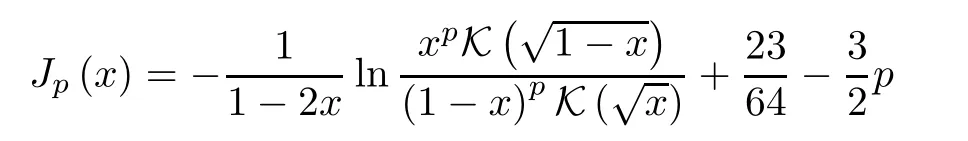
is absolutely monotonic on (1/2，1)，and completely monotonic on (0，1/2);so is-J0(x).

ProofUsing the power series expansion (3.9)，we have that

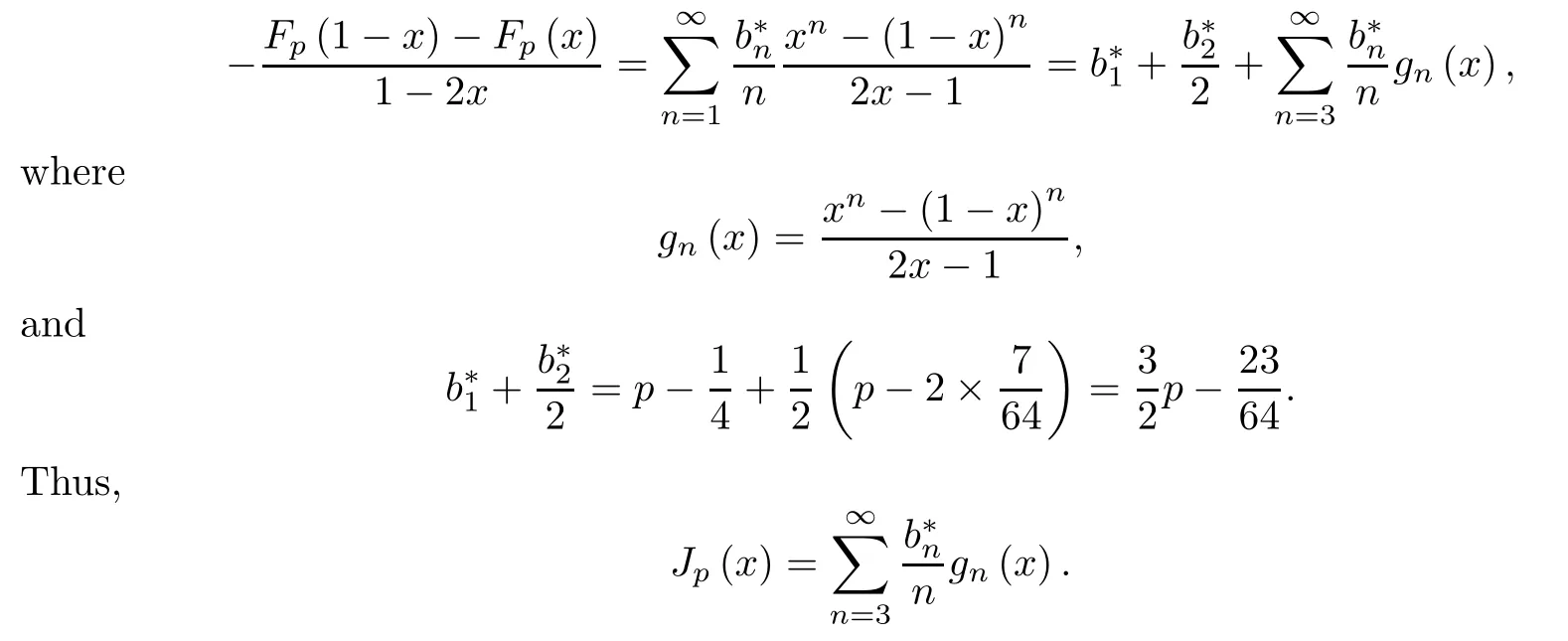
Making a change of variablex=(t+1)/2，namely，t=2x-1∈(-1，1)，gn(x) can be expressed as

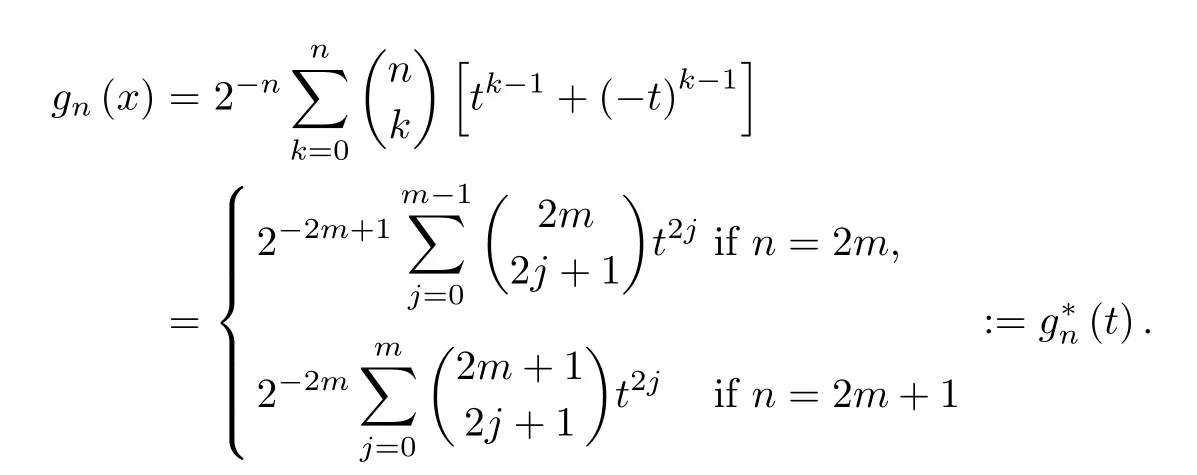
Then，(i) In the case ofp≥13/64，by Lemma 3.2，it is seen thatforn≥3.Since(t) is even on (-1，1) and(t) is clearly absolutely monotonic on (0，1)，so isgn(x) on (1/2，1).Then(t) is completely monotonic on (-1，0)，and so isgn(x) on (0，1/2).It then follows thatJp(x) is absolutely monotonic on (1/2，1) and completely monotonic on (0，1/2).

(ii) In the case ofp=0，we have that

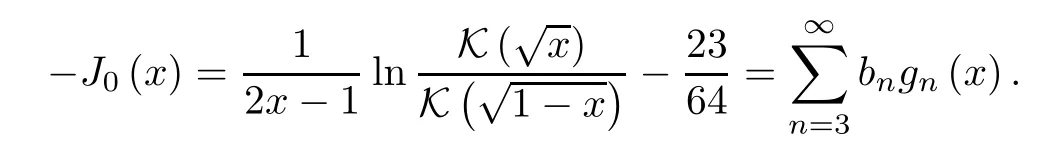
Sincebn＞0 forn≥1，by Lemma 3.2，clearly，the function-J0(x) has the same higher monotonicity asJp(x) forp≥13/64.Thus the proof is finished. □

Remark 4.12The complete monotonicity has many applications in the gamma，polygamma functions，as is shown in[44–46]，and it seems to be rare in hypergeometric functions;and Proposition 4.11 provides an example of precisely this.

4.3 Bounds for the product K (r) K (r′)

It was proven in[31，Corollary 3.13]that，forr∈(0，1)，

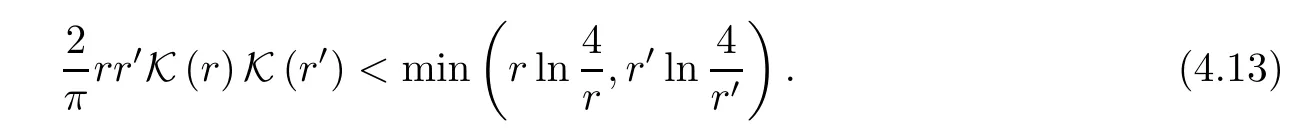
Another similar inequality，

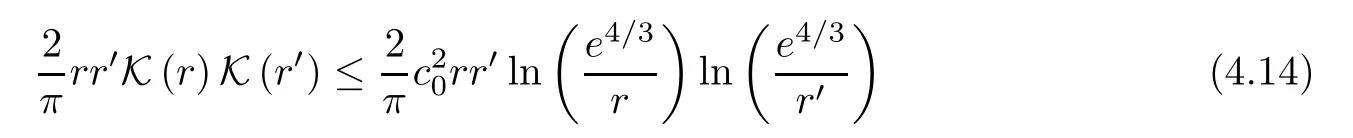
forr∈(0，1)，appeared in[34，Corollary 2]，whereWe now give a double inequality that arises by Theorem 1.2.

Proposition 4.13The double inequality

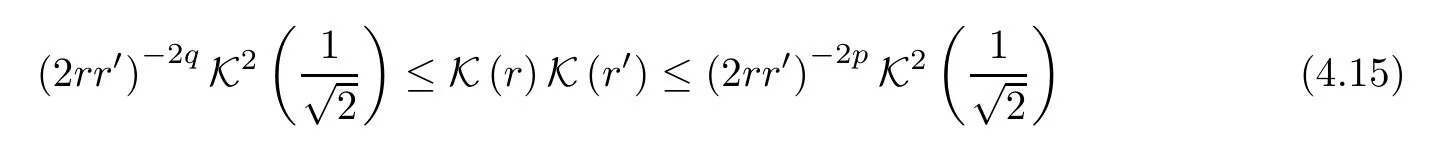
holds forr∈(0，1) if and only ifp≥7/32 andq≤0，where the equalities hold if and only if

ProofTheorem 1.2 shows thatis convex on (0，1) ifp≤0 and concave ifp≥7/32.By Jessen inequality，we have that

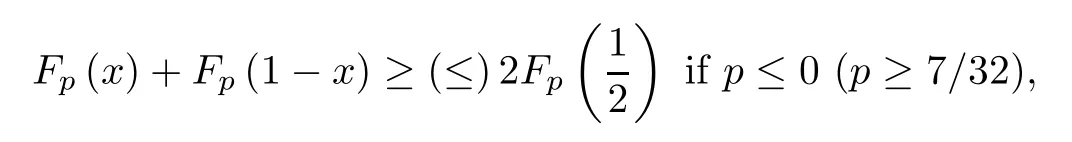
which，by lettingx=r2，implies that the double inequality (4.15) holds forr∈(0，1) ifp≥7/32 andq≤0.This completes the proof. □

Remark 4.14Takingq=0 andp=1/4 in (4.15) yields that

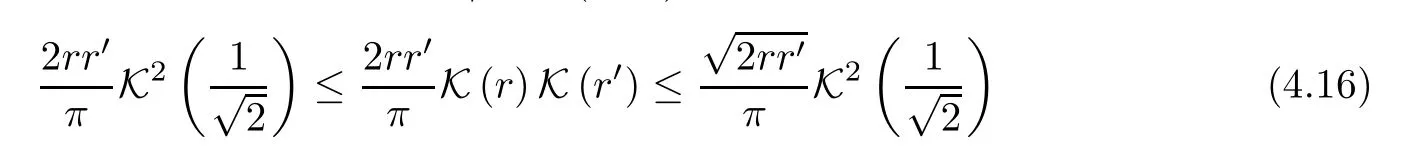
forr∈(0，1).The upper bound in (4.16) is not comparable with those in (4.13) and (4.14)，while the lower bound in (4.16) seems to be a newcomer.

A functionf:(a，∞)→R is said to be superadditive if

If-fis superadditive，thenfis said to be subadditive on (a，∞)(see[47]).It is known that every convex functionf:[0，∞)→R satisfies a functional inequality

by Theorem 1.2 we immediately get

Proposition 4.15The function

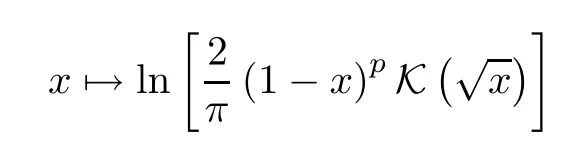
is superadditive (subadditive) on (0，1) ifp≤0(p≥7/32).Or，equivalently，ifp≥7/32 andq≤0，then

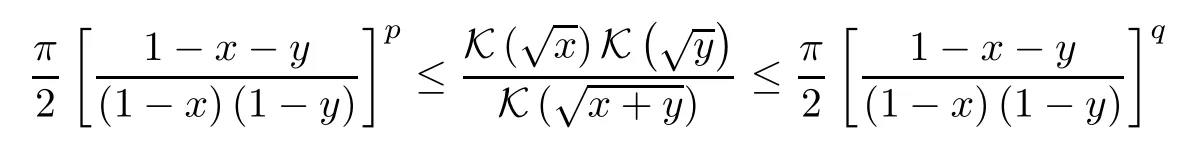
forx，y，x+y∈(0，1).

5 Conclusions

In this paper，we found the necessary and sufficient conditions for the functionsFp(x)，(x)(i=1，2，3) to be absolutely monotonic on (0，1) by using the recurrence method.Applying Theorem 1.2，we established some new bounds for the ratios and the product of two complete integrals of the first kind.These new bounds improved upon and refined some known results.