A COMPACTNESS THEOREM FOR STABLE FLAT SL (2，C) CONNECTIONS ON 3-FOLDS*

Teng HUANG (黄腾)

School of Mathematical Sciences，University of Science and Technology of China;CAS Key Laboratory of Wu Wen-Tsun Mathematics，University of Science and Technology of China，Hefei 230026，China

E-mail:htmath@ustc.edu.cn;htustc@gmail.com

Abstract Let Y be a closed 3-manifold such that all flat SU (2)-connections on Y are non-degenerate.In this article，we prove a Uhlenbeck-type compactness theorem on Y for stable flat SL (2，C) connections satisfying an L2-bound for the real curvature.Combining the compactness theorem and a result from[7]，we prove that the moduli space of the stable flat SL (2，C) connections is disconnected under certain technical assumptions.

Key words Stable flat SL (2，C) connections;Vafa-Witten equations;compactness theorem

1 Introduction

LetXbe an oriented，closed，smoothn-dimensional manifold with a smooth Riemannian metricg，and letPbe a principalG-bundle overX，withGbeing a compact Lie group.We denote by APthe set of all connections onP，and by Ωk(X，gP) the set of gP-valuledk-forms，where gPis the adjoint bundle ofP.Suppose thatAis a connection onPand its curvature is denoted byFA∈Ω2(X，gP).For any connectionAonP，we have the covariant exterior derivativesdA:Ωk(X，gP)→Ωk+1(X，gP).The curvature

of the complex connection A:=A+iφis a 2-form with values in.We say that A=A+iφis a complex flat connection with the moment map condition，if the pair (A，φ) satisfies

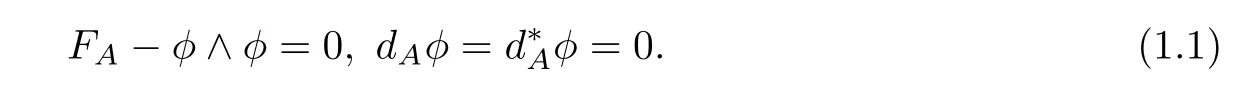
The system of the pairs (A，φ) is elliptic[4].For convenience，we call the solutions of the elliptic system stable flat connections (see[1]).These equations are not only invariant under the actions of the real gauge group GP=C∞(P×GG)，but also invariant under the actions of the complex gauge groupThe solution of stable flat connections on the compact Riemannian surface Σ is also a solution of Hitchin’s equation[6].The moduli space of the solutions of Hitchin’s equation which satisfyis compact;see[4，Theorem 4.1].Following[3，Proposition 2.2.3]or[10，Proposition 1.2.6]，we know that the gauge-equivalence classes of flat connections over a connected manifold，X，are in one-to-one correspondence with the conjugacy classes of representationsπ1(X)→G.

The Uhlenbeck compactness theorem[17，20]on the moduli space of the connections withLp-bounds on curvature is one of the most fundamental theorems in the analytical part of gauge theory.In[13]，Taubes studied the Uhlenbeck style compactness problem forSL(2，C) connections，including solutions to the above equations，for the three-and four-manifolds[13–15].

We denote by

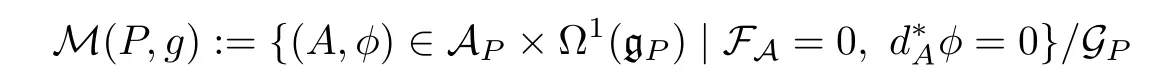
the moduli space of the stable flatSL(2，C) connections.In particular，the moduli space of gauge-equivalence classes[Γ]of flat connections Γ onP，

can be embedded into M (P，g) via the mapA(A，0).The Uhlenbeck compactness theorem[17]shows that the moduli spaceM(P，g) is compact.

One can see that the pair (A，φ) has the a priori estimate (see[4])

wherec0is a positive constant dependent on the metricg.Then the Uhlenbeck compactness theorem implies that the moduli space of solutions of stable flatSL(2，C) connections satisfying (1.1) withis compact for every given positive constantK.On the other hand，there are examples of sequences of solutions (Ai，φi) to (1.1) such that ‖φi‖L2(X)diverges to infinity，therefore the moduli space of solutions to (1.1) is not always compact.An interesting question to ask is the following:

LetKbe a positive constant number，and consider the subset of M (P，g) consisting of (A，φ) such that ‖FA‖L2(X)≤K，is this subset always compact?

In this article，we consider the case for the stable flatSL(2，C) connections on a closed，smooth，oriented three-manifoldY.We will give a positive answer to the question above ifY，GandPsatisfy certain conditions.

We denote by

the self-dual operator with respect to a flat connection Γ.We recall the definition of nondegenerate flat connections as follows (see[2，Definition 2.4]):

Definition 1.1LetGbe a compact Lie group，and letPbe aG-bundle over a closed，smooth manifoldXof dimensionn≥2，endowed with a smooth Riemannian metricg.The flat connection Γ is called non-degenerate if

The main observation of this article can be stated as follows:

Theorem 1.2(A compactness theorem for stable flatSL(2，C) connections with bounded real curvatures) LetYbe a closed，oriented，smooth Riemannian three-manifold，and letPbe a principalSU(2) orSO(3)-bundle overY.Let{(Ai，φi)}i∈Nbe a sequence ofC∞-solutions of Equations (1.1).Suppose that all flat connections on the principal bundlePare non-degenerate.If theL2-norms of the curvatures ‖FAi‖L2(Y)are bounded，then there is a subsequence of Ξ⊂N and a sequence of gauge transformations{ui}i∈Ξsuch thatconverges to a pair (A∞，φ∞) obeying Equations (1.1) onPin theC∞-topology.In particular，the moduli space of solutions of stable flatSL(2，C) connections，which obeysRY|FA|2≤K，is compact，for every positive constantK.

Remark 1.3Taubes[13]considered a sequence of complex connections Ai:=Ai+iφisuch that theL2-norms ofFAiare bounded (in this article，the complex curvature is just zero).There are two possible cases:(1) if ‖φi‖L2(X)has a bounded sequence，then Taubes provesin theC∞-topology;(2) if ‖φi‖L2(X)has no bounded sequence，then Taubes makes sense of the limit as a Z2harmonic spinor.In particular，if the sequence ‖FAi‖L2(Y)is divergent to infinity，then following inequality (1.2)，one can see that the sequence ‖φi‖L2(Y)is also divergent to infinity.

As a particular case of Theorem 1.2，we have anL2-bound on the extra fields in the fibre direction at a connectionA0.Namely，we have

Corollary 1.4LetYbe a closed，oriented，smooth Riemannian three-manifold，and letPbe a principalSU(2) orSO(3)-bundle overY.Suppose that all flat connections on the principal bundlePare non-degenerate.Then for any sequence of solutions{(A0，φi)}i∈Nof Equations (1.1)，there exists a subsequence Ξ⊂N and a positive constantC＞0 such thatfor alli⊂Ξ.

Corollary 1.4 is similar to the Vafa-Witten equations case;see[12，Corllary 1.4].

Following the notation of[3，Section 4.2.1]，we denote by ([A，φ]) the equivalence class of a pair (A，φ)，that is，a point in M (P，g).We denote

We can define a distance function on M (P，g) as follows:

We can use the compactness theorem 1.2 to study the topology of the moduli space of stable flatSL(2，C) connections.

Theorem 1.5Assume the hypotheses of Theorem 1.2.Suppose that all flat connections on the principalG-bundlePare non-degenerate.If (A，φ) is aC∞-solution of Equations (1.1)，then there is a positive constantsuch that

unlessAis a flat connection.

Remark 1.6There are many combinations of conditions onG，P，Yandg，which imply that the flat connection is non-degenerate.For example，ifYis a closed，oriented Riemannian three-manifold with the homology ofS3andPis a principalSU(2)-bundle overY，then every flat connection Γ onPis non-degenerate.

Corollary 1.7LetYbe a closed，oriented，smooth Riemannian three-manifold with the homology ofS3，and letPbe a principalSU(2)-bundle.Let{(Ai，φi)}i∈Nbe a sequence ofC∞-solutions of Equations (1.1).If theL2-norms of the curvatures ‖FAi‖L2(Y)have a bound，then there is a subsequence of Ξ⊂N and a sequence of gauge transformations{ui}i∈Ξsuch thatconverges to a pair (A∞，φ∞) obeying Equations (1.1) onPin theC∞-topology.Furthermore，there is a positive constant(P，g)∈(0，1]such that

unlessAis a flat connection.

The organization of this paper is as follows:in Section 2，we first recall the compactness theorem of the Vafa-Witten equations，which was proved by Tanaka[12].We also observe that the set of stable flatSL(2，C) connections on a compact 3-foldYis in one-to-one correspondence with solutions toS1-invariant Vafa-Witten equations onY×S1.Then，by Tanaka’s compactness theorem，we can prove a compactness theorem for stable flatSL(2，C) connections.In Section 3，we obtain，by our compactness theorem，a topological property of the moduli space of stable flatSL(2，C) connections.

2 Compactness Theorem for Stable SL (2，C) Flat Connections

2.1 Vafa-Witten equations and stable SL(2，C) flat connections

In this section，we recall the compactness theorem of Vafa-Witten equations，which was proved by Tanaka[12].For an oriented 4-dimensional Riemannian manifoldXwith metricg，the Hodge star operator*:Ω2(X)→Ω2(X) induces the following splitting:

Accordingly，the space of gP-valued two-forms Ω2(X，gP) splits as

We begin by defining the Vafa-Witten equations[19].One also can see Equations (2.4)–(2.5) in[12].We call the pair (A，B)∈AP×Ω2，+(X，gP) a solution of Vafa-Witten equations if (A，B) satisfies

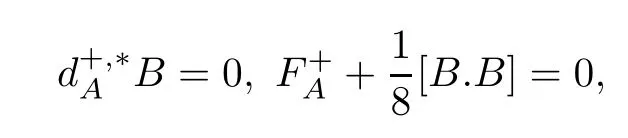
where[B.B]∈Ω2，+(X，gP) is defined as in[11，Appendix A].Vafa-Witten equations were introduced by Vafa and Witten to studyS-duality in a twist of the N=4 supersymmetric Yang-Mills theory[19].By appropriately counting the number of points of the moduli space of Vafa-Witten equations，we hope to obtain a numberV W(P)，called the Vafa-Witten invariant for the principal bundleP→X[11，Section 1.3].These equations were also considered by Haydys[5]and Witten[21]from a different point of view.

LetGbe a Lie group and letPbe a principalG-bundle over a smooth Riemannian manifoldX.We recall the equivalent characterizations of flat bundles[10，Section 1.2]，that is，bundles admitting a flat connection.

Proposition 2.1([10，Proposition 1.2.6]) For a principalG-bundlePoverX，the following three conditions are equivalent:

(1)Padmits a flat structure;

(2)Padmits a flat connection;

(3)Pis defined by a representationρ:π1(X)→G.

Proposition 2.2If (A，φ) is aC∞-solution of (1.1) over a closedn-manifoldX，then

We now return to the setting of this article.LetYbe an oriented，smooth，Riemannian three-manifold，and letPbe aG-principal bundle overYwithGbeing a compact Lie group.We denote byX:=Y×S1the product manifold with the product metric.We pull back a connectionAonP→Ytop*1(P)→Xvia the canonical projection

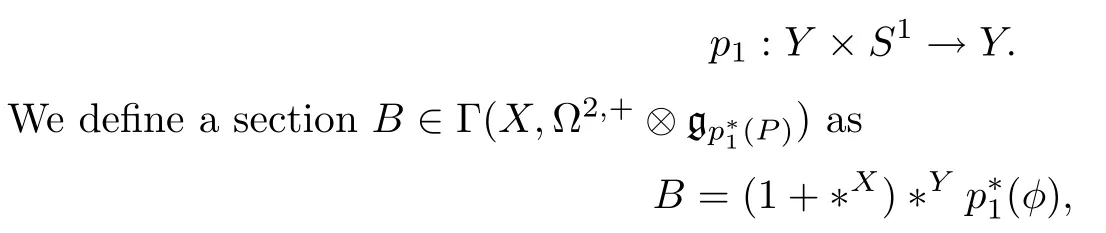
where*Y(resp.*X) is the Hodge star operator with respect to metricgY(resp.gX).We then have

Proposition 2.3The canonical projection gives a one-to-one correspondence between stable flat connections onPandS1-invariant Vafa-Witten equations on the pullback bundle(P).

ProofThe proof is similar to that of[11，Lemma 8.2.2].In a local coordinate{e1，e2，e3}ofT*Y，we can denote

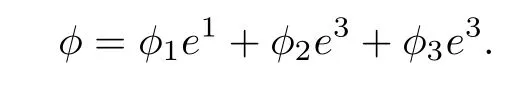
Note that

Then，by the definition ofB，we get

We also observe that

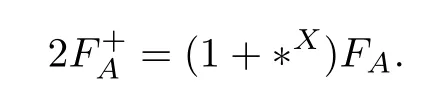
Therefore，we have

We also have another equation:

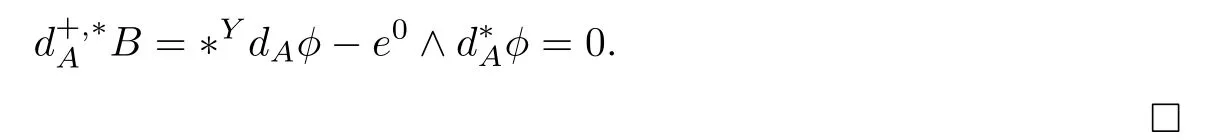
2.2 Compactness theorem for Vafa-Witten equations

Mares studied the analytic aspects of Vafa-Witten equations in[11].We do not have anyL2-bounded on the curvatureFAof a connectionAwhich satisfies the Vafa-Witten equations as in the case of Hitchin-Simpson equations[6].Mares observed that if (A，B) is a solution of Vafa-Witten equations and theL2-norm ofBhas a uniform bound，then the curvatureFAalso has a uniform bound in theL2-norm by the identity

where ⊙ denotes some bilinear on Ω2，+(X，gP)⊗Ω2，+(X，gP)，sis the scalar curvature of the metric，andW+is the self-dual part of the Weyl curvature of the metric (see[12，Page 1204]or[11，Section B.4]for more details).Following the Uhlenbeck compactness theorem，Mares obtained a compactness theorem of Vafa-Witten equations under the extra fieldsBthat have a bound in theL2-norm[11].

For a sequence of connections{Ai}onP，Tanaka defined a setS({Ai}) as follows:

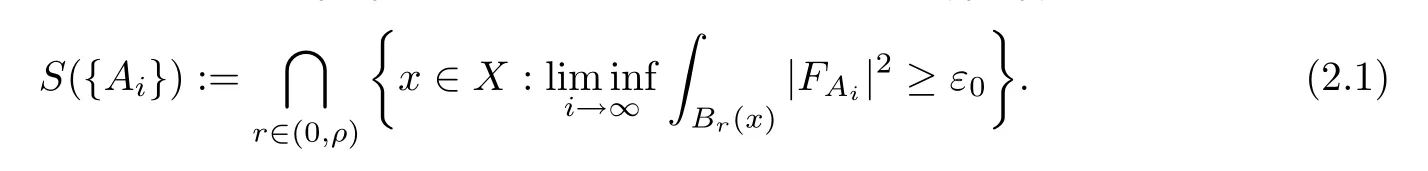
Hereε0is a positive constant which is defined as in[12].This setS({Ai}) describes the singular set of a sequence of connections{Ai}.In[12]，Tanaka observed that under the particular circumstance where the connections are non-concentrating and the limiting connection is nonlocally reducible，one obtains anL2-bound on the extra fields.Here，we say that a connectionAon a principalSU(2) orSO(3) bundlePis locally reducible if the vector bundle gPhas a one-dimensional subbundle that isA-covariantly constant (see[12，Definition 2.1]).Note that a connection on a principalSU(2) orSO(3) bundlePbeing locally reducible is the same as being honestly reducible ifXis simply connected.The following is an analogue of the second part of[16，Theorem 1.1]，but under the assumption thatS({Ai}) is empty:

Theorem 2.4([16，Theorem 1.2]and[12，Proposition 4.4]) Let{(Ai，Bi)}be a sequence of solutions of Vafa-Witten equations，and setri:=‖φi‖L2(X).Letδdenote the injectivity radius ofX.Suppose that there existr∈(0，δ) and a sequence Ξ⊂N such that

for everyi∈Ξ andx∈X.Assume that the sequence{ri}i∈Nhas no bounded subsequence.Then there exist a closed，nowhere dense setZ⊂X，a real line bundle I→X-Z，a sectionν∈Γ(X-Z，I⊗Ω2，+)，a connectionAΔonP|X-Z，and an isometric bundle homomorphismσΔ:I→gP.Their properties are as follows:

(a)Zis the zero locus of|ν|;

(b) the function|ν|is Hlder continuousC0，1/κonX;

(c) the sectionvis harmonic in the sense of dν=0;

(d)|∇ν|is anL2-function onX-Zthat extends as anL2-function onX;

(e) the curvature tensor ofAΔis anti-self-dual;

(f) the homomorphismσΔisAΔ-covariantly constant.

In addition，there exist a subsequence Λ⊂Ξ and a sequenceuiof automorphisms fromPsuch that

2.3 Proof of our results

In this section，we give the proof of our main result.First，we observe

Proposition 2.5LetYbe a closed，oriented，smooth Riemannian three-manifold，and letPbe a principalG-bundle withGbeing a compact Lie group.Let{Ai}i∈Nbe a sequence ofC∞-connections onPwith theL2-norms of the curvatures ‖FAi‖L2(X)having a uniform bound.We denote by{Ai}the pullbackS1-invariant connections.Then the setS({Ai}) is empty，whereS(·) is defined in Equation (2.1).

ProofFor a point (y0，θ0)∈Y×S1，we denote by

the geodesic ball onY×S1.Hence，we have

We can choosersufficiently small such that

whereκis the constant on Theorem 2.4.This complete proof. □

Following the idea in the proof of[15，Theorem 1.2]，we can obtain a compactness theorem for the stable flatSL(2，C) connections on the three-manifold.

Theorem 2.6LetYbe a closed，oriented，smooth Riemannian three-manifold，and letPbe a principalG-bundle withGbeingSU(2) orSO(3).Let{(Ai，φi)}i∈Nbe a sequence ofC∞-solutions of Equations (1.1)，and setri:=‖φi‖L2(X).Suppose that theL2-norms of the curvatures ‖FAi‖L2(Y)have a uniform bound and that the sequence{ri}i∈Nhas no bounded subsequence.Then there exist a closed，nowhere dense setZY⊂Y，a real line bundle IY→Y-ZY，a sectionν∈Γ(Y-ZY，IY⊗Ω1)，a connectionAΔonP|Y-ZY，and an isometric bundle homomorphismσΔ:IY→gP.Their properties are as follows:

(a)ZYis the zero locus of|ν|;

(b) the sectionvis harmonic in the sense ofdν=d*ν=0;

(c) the curvature tensor ofAΔis flat;

(d) the homomorphismσΔisAΔ-covariantly constant.

In addition，there exist a subsequence Λ⊂Ξ and a sequenceuiof automorphisms fromPsuch that

ProofAs explained momentarily，this theorem constitutes a special case of Theorem 2.4.To obtain Theorem 2.6 from Theorem 2.4，we takeXin Theorem 2.6 to be the productY×S1with the metric being the product metric.The pull-back of the principalG-bundlePonYtoXvia the projection map toYdefines a principalG-bundle overX;the latter is denoted also byP.Let{(Ai，φi)}be a sequence of solutions of stable flatSL(2，C) connections overY.For simplicity，we keep the same notations for objects onYand their pullbacks toX.We denote thatBi=(1+*X)*Yφi.If we suppose that the sequence{ri:=‖φi‖L2(Y)}i∈Nhas no bounded subsequence，then ‖Bi‖L2(X)also has no bounded subsequence.A similar sort of argument can be used to prove that Theorem 2.4’s setZis the product ofS1and a closed setZY⊂Y，and that Theorem 2.4’s real line bundle I is isomorphic to the pull-back via the projection map of a real line bundle defined on the complement inYofZY;this denoted for now by IY.Moreover，such an isomorphism identifies Theorem 2.4’s version ofνwith the pull-back of a harmonic，IYvalued 1-form onY-ZY，withZYdenoting the locus where its norm is zero. □

Remark 2.7Taubes considered a sequence of complex connections{Ai:=Ai+iφi}such that theL2-norms of{FAi}are bounded.If{‖φi‖L2(X)}has no bounded sequence，then Taubes makes sense of the limit as a Z2harmonic spinor[15].In our result，we add the conditions that all connections{Ai}are stable flatSL(2，C) connections and the real curvatures{FAi}areL2-bounded，so we prove the limit as a decoupled stable flatSL(2，C) connection.

The next theorem is a special case of Theorem 1.1b in[15]，and implies，among other things，thatZYhas a measure of zero.To set the notation for this upcoming theorem，we note that a pointp∈ZYis a point of discontinuity for IYif IYis not isomorphic to the product bundle on the complement ofZYin any neighborhood ofp[15].

Theorem 2.8([15，Theorem 1.1b]) LetZYand IYbe as described in Theorem 2.6.The setZYhas a Hausdorffdimension of at most 1，and moreover，the set of the points of discontinuity for IY(defined in the preceding paragraph) are the points in the closure of an open subset ofZYthat is an embeddedC1curve inYdenoted by Σ.

Uhlenbeck’s[17]theorem applies to the connections onPand，in particular，makes the following assertion:

Uhlenbeck’s TheoremLet{Ai}i∈Nbe a sequence of connections onPover a closed，oriented，3-manifold.If theL2-norms of the curvaturesFAiof the connections{Ai}have a uniform bound，then there is a subsequence Ξ⊂N and a sequence of gauge transformations{ui}i∈Ξsuch thatconverges weakly in the-topology to a connectionA∞onP.

By the a priori estimate (1.2)，we then have

Theorem 2.9([15，Theoreom 1.1a]) LetYbe a closed，oriented，smooth Riemannian three-manifold，and letPbe a principalSU(2) orSO(3)-bundle overY.Let{(Ai，φi)}i∈Nbe a sequence ofC∞-solutions of Equations (1.1).Suppose that the sequence{‖φi‖L2(Y)}has a bounded subsequence.Then there is a subsequence of Ξ⊂N and a sequence of gauge transformations{ui}i∈Ξsuch thatconverges to a pair (A∞，φ∞) obeying Equations (1.1) onPinC∞-topology.

We are finally ready to use the above results in the following proposition:

Proposition 2.10LetZYand IYbe as described in Theorem 2.6，so thatσΔandAΔare defined overY-ZY.Then we have that

(1) There exists a smooth flat connectionA∞defined over all ofY，and a Sobolev classgauge transformationu∞defined overY-ZYsuch thatis restricted toY-ZYofA∞.DefiningoverY-ZY，we then have that∇A∞σ∞=0.

(2) The bundle IYoverY-ZYextends to a bundle defined over all ofY，which we again denote by IY.

(3) There exist extensions of bothv∈Γ(IY⊗Ω1) andσ∞:IY→gPto all ofY.We again denote these byvandσ∞.The extensions satisfy dv=0 and∇A∞σ∞=0.

ProofThe idea of our proof is similar to that of[12，Proposition 4.6].

We first prove item 1.Following the weak Uhlenbeck compactness theorem (see[20，Theorem A])，for any sequence{Ai}i∈Nwith boundedL2-curvature{FAi}i∈Non a principalGbundle over a closed three-manifold，there exists a subsequence (again denote{Ai}i∈N) and a sequence of gauge transformations{ui}i∈Nsuch that(Ai) converges weakly to a limit connectionA∞over all ofYinRecall from Theorem 2.6 thatAΔis thelimit over compact subsetY-ZYof gauge equivalent connections.Since weaklylimits preservegauge equivalence，it follows that there exists a Sobolev-classgauge transformationu∞such that

Note thatAΔis flat and gauge-equivalent over the complement ofZYtoA∞.Thus，A∞is anconnection whose curvature isL2，and vanishes on the completion ofZY，which，by Theorem 2.8，is a set of measure zero.Hence the curvature ofA∞is flat and so a standard elliptic regularity argument can be used to prove that there is anand aC0automorphism ofPthat transformsA∞into a smooth flat connection.After possibly composingu∞with such an automorphism，we may assume，without loss of generality，thatA∞is smooth and thatu∞is continuous.We also have that∇A∞σ∞=0 follows from Theorem 2.6，sinceσΔisAΔ-covariantly constant.This establishes item 1.

We next prove item 2，by which IYextends overZY.Let Σ⊂ZYdenote theC1submanifold that is described by Theorem 2.8.It is enough to prove that Σ is empty.For this purpose，assume to the contrary that ΣØ and letS⊂Σ be a component.This is aC1embedded curve.Fix a pointp∈S.SinceSisC1，there is an embedded diskD⊂Yclosure intersects thatStransversally at a single point which isp.This is also its only intersection point withZY，sinceSis an open subset ofZY.Sincepis a point of discontinuity for the bundle IY，the restriction of IYtoD-{p}is not isomorphic to the product line bundle.In particular，parallel transport byAΔofσΔalong any circle inD-{p}which wraps once aroundpgives-σΔ.However，AΔis gauge-equivalent to a connection which is smooth over all ofD.This parallel transport around a sufficiently small bounded interval will be arbitrarily close to+σΔ，which is a contradiction.

Finally，we prove item 3 by showing that bothvandσ∞extend to all ofYassections.Granted this extension，we may argue as in item 1 that both dvand∇A∞σ∞areL2sections which vanish almost everywhere，and hence，by elliptic regularity，vandσ∞are smooth and satisfy dv=0 and∇A∞σ∞=0 over all ofY. □

Following the above results，we can prove a Uhlenbeck-type compactness theorem onYfor stable flatSL(2，C) connections satisfying anL2-bound for the real curvature.

Proof of Theorem 1.2We setri:=‖φi‖L2(Y).First，we can prove that there exists a subsequence Ξ⊂N such that{ri}i∈Ξhas a uniform bound.If not，then the sequence{ri}i∈Nhas no bounded subsequence.We denoteA∞，νandσ∞as described in Proposition 2.10.Hence，following Proposition 2.10，we have

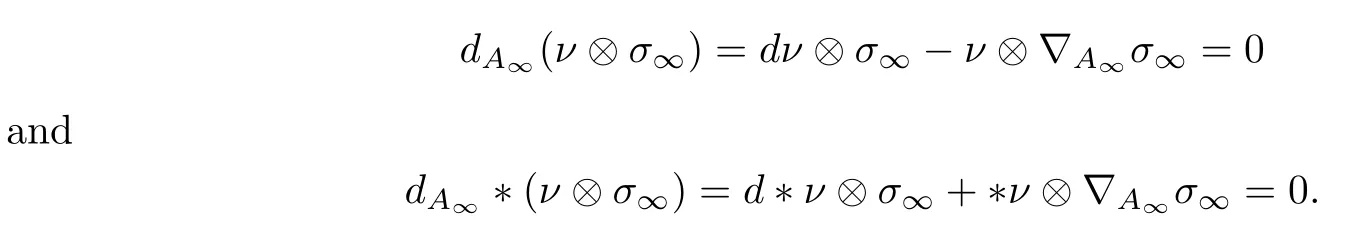
Sinceν⊗σ∞∈Ω1(Y，gP)，the hypothesis of the flat connectionA∞implies that

Following item 1 in Proposition 2.10，there exists a continuous Sobolev-classgauge transformationu∞defined overY-ZYsuch that

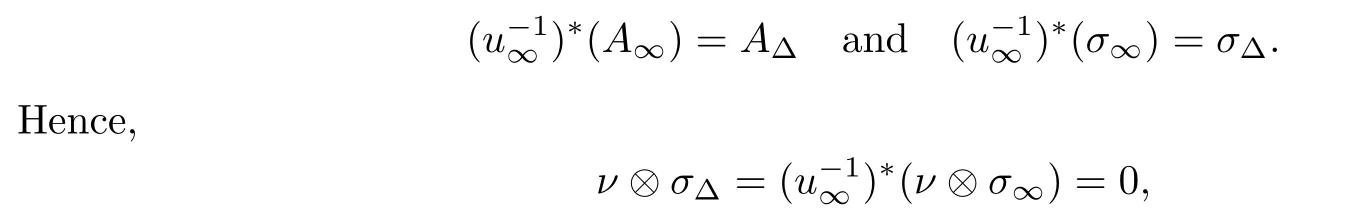
onY-ZY.The zero locus of the extension of|ν|is the setZY，and we can set thatσΔis a unit length，AΔ-covariantly constant homomorphism overY-ZY.Hence，we can say that|ν|=0 onY.

On the other hand，following the last item in Theorem 2.6，there exist a subsequence Ξ⊂N and a sequence{ui}i∈Ξof automorphisms fromPsuch thatconverges toν⊗σΔin the-topology on compact subset inY-ZYand theC0-topology onY.Meanwhile，converges to|ν|in the weakly-topology and theC0-topology on the whole ofY.Hence

That contradicts the fact that，∀i∈N.In particular，the preceding argument shows that there exists a subsequence Ξ⊂N such that{ri}i∈Ξhas a uniform bound.Thus following Theorem 2.9，there is a subsequence (again denote by{(Ai，φi)}i∈Ξ) and a sequence of the gauge transformation{ui}i∈Ξsuch thatconverges to a pair (A∞，φ∞) onPin theC∞-topology. □

Corollary 2.11LetYbe a closed，oriented Riemannian three-manifold with the homology ofS3，and letPbe a principalSU(2)-bundle.Let{(Ai，φi)}i∈Nbe a sequence ofC∞solutions of Equations (1.1).If theL2-norms of the curvatures ‖FAi‖L2(Y)have a uniform bound，then there is a subsequence of Ξ⊂N and a sequence of gauge transformations{ui}i∈Nsuch thatconverges to a pair (A∞，φ∞) obeying Equations (1.1) onPin theC∞-topology.

3 Disconnectedness of the Moduli Space M (P，g)

3.1 A lower positive bound of extra fields

We call a stable flat connection A:=A+iφdecoupled if the real connectionAis flat and the extra fieldφis a harmonic gP-1-form with respect to，i.e，

Using a result of Uhlenbeck[18]，we observe that if we have the stable flat connection A over a closed，smooth，Riemannian three-manifoldY，then theL2-norm of extra fields has a uniform positive lower bound unless the real connection is flat.

Theorem 3.1([7]) LetYbe a closed，oriented，Riemannian three-manifold and endowed with a smooth Riemannian metricg，and letPbe a principalG-bundle withGbeing a compact Lie group.If (A，φ) is aC∞-solution of equations (1.1)，then there is a positive constantC=C(X，g，G) such that ‖φ‖L2(Y)≥C，unlessAis a flat connection.

Suppose that all flat connections onPare non-degenerate.Then the extra fields vanish if the stable flat connectionA+iφis decoupled over a closed Riemannian manifold.Following Theorem 3.1，we then have

Corollary 3.2Assume the hypothesis of Theorem 3.1.Suppose that all flat connections on the principal bundlePare non-degenerate.If (A，φ) is aC∞-solution of equations (1.1)，then either there exists a positive constantC=C(X，g，G) such that ‖φ‖L2(Y)≥Corφvanishes.

3.2 A lower positive bound of curvatures

One can see thatM(P，g) is the space of real flat connections and that M′(P，g):=M (P，g)M(P，g) is the space of real connections that are non-flat.Hence we can denote by

the distance betweenM(P，g) and M′(P，g).Following Theorem 3.1，we can obtain a topological property of the moduli space M (P，g).

Proposition 3.3(Disconnectedness of the moduli space M (P，g)) LetYbe a closed，oriented，smooth，Riemannian three-manifold，and letPbe a principalG-bundle withGbeing a compact Lie group.Suppose that all flat connections on the principal bundlePare nondegenerate.If the moduli spacesM(P，g) and M′(P，g):=M (P，g)M(P，g) are all non-empty，then the moduli space M (P，g) is disconnected.

ProofUnder the hypothesis of the flat connection，following the Corollary 3.2，theL2-norm of the extra field ‖φ‖L2(X)has a lower bound unlessφvanishes.If the moduli spacesM(P，g) and M (P，g)M(P，g) are all non-empty，then

whereC=C(Y，g) is the positive constant in Corollary 3.2，i.e.，the moduli space M (P，g) is disconnected. □

We extend the idea in[9]to a stable flatSL(2，C) connection case，and we prove a gap result of the real curvature following the compactness theorem 1.2.

Proposition 3.4LetYbe a closed，oriented，smooth，Riemannian three-manifold，and letPbe a principalG-bundle withGbeingSU(2) orSO(3).Suppose that all flat connections on the principal bundlePare non-degenerate.If the pair (A，φ) is aC∞-solution of equations (1.1)，then there is a positive constantC=C(Y，g，P) such that ‖FA‖L2(Y)≥C，unless the real connectionAis flat.

ProofSuppose that the constantCdoes not exist.We may then choose a sequence{(Ai，φi)}i∈Nsuch that ‖FAi‖L2(Y)→0 asi→∞，and that{Ai}i∈Nare all non-flat.Thus the compactness Theorem 1.2 implies that there exists a pair (A∞，φ∞) that obeys equations (1.1)，and that there is a sequence of gauge transformations{ui}i∈Ξsuch that (u*i(Ai)，u*i(φi))→(A∞，φ∞) inC∞overY.Following Theorem 3.1，theL2-norm of extra field ‖φ∞‖L2Xhas a positive lower bound.Therefore，we have

whereC=C(Y，g) is a positive constant.

On the other hand，since ‖FAi‖L2(Y)→0，the weak Uhlenbeck compactness theorem implies that the connectionA∞onPis flat.HenceA∞is non-degenerate，by the hypothesis on this proposition，which implies the extra fieldφ∞≡0.This is in contradiction to the fact that ‖φ∞‖L2(Y)has a uniform positive lower bound. □

Remark 3.5The solutions of stable flat connections also satisfy the complex Yang-Mills equations[4].The author proved that if the pair (A，φ) is a smooth solution of a stable flat connection over a closed，smooth，Riemanniann-manifoldX，the curvatureFAof a non-flat connectionAhas a uniform positive lowerLp-bound under the condition that all flat connections are all non-degenerate;see[8，Theorem 1.2].

Proof of Theorem 1.5First，we give the a priori estimate for the curvature of a connection.Since

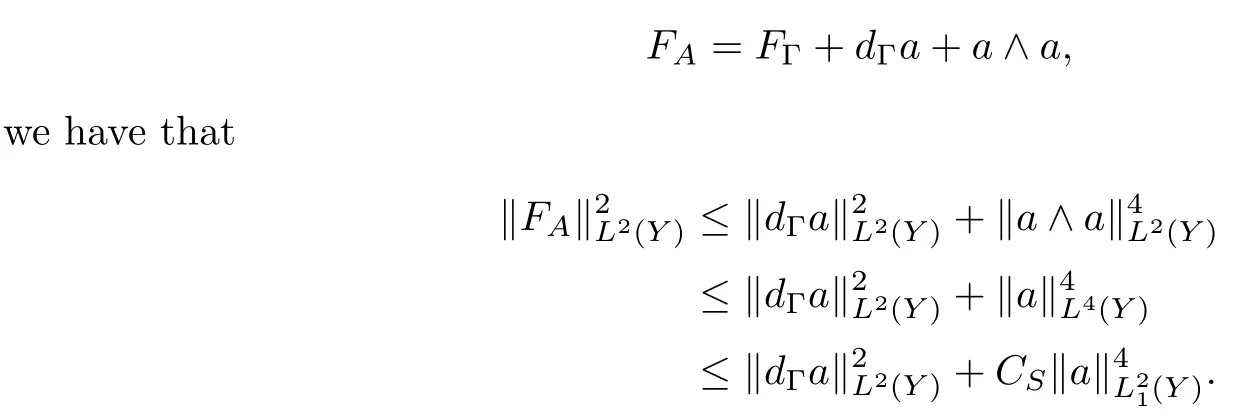
In the last inequality，we used the Sobolev embeddingfor 2≤p≤6 with the embedding constantCS.Here

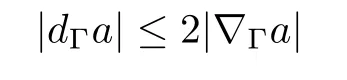
due to the fact that

for allU，V∈Ty(Y).Combining the preceding inequalities yields that

wherec=c(Y，g) is a positive constant.

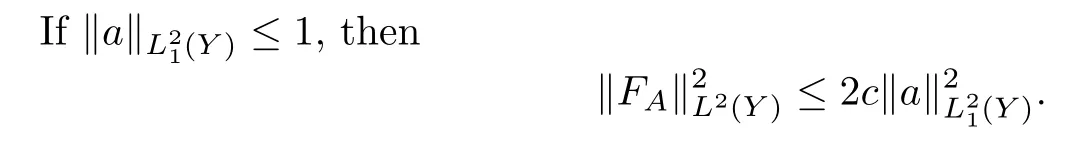
Therefore，we have

whereCis the positive constant in Proposition 3.4.We set，and thus

This complete the proof. □

AcknowledgementsI would like to thank the anonymous referees for careful reading of the manuscript and for helpful comments.I would like to thank Y.Tanaka for kind comments regarding this and the companion article[12].