THE SYSTEMS WITH ALMOST BANACH-MEAN EQUICONTINUITY FOR ABELIAN GROUP ACTIONS*
2022-06-25BinZHU朱斌
Bin ZHU (朱斌)
College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China
E-mail:binzhucqu@163.com
Xiaojun HUANG (黄小军)†
College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China
Chongqing Key Laboratory of Analytic Mathematics and Applications,Chongqing University,Chongqing 401331,China
E-mail:hxj@cqu.edu.cn
Yuan LIAN (连媛)
Department of Mathematics,Taiyuan Normal University,Jinzhong 030619,China
E-mail:Andrea@tynu.edu.cn
Abstract In this paper,we present the concept of Banach-mean equicontinuity and prove that the Banach-,Weyl-and Besicovitch-mean equicontinuities of a dynamic system of Abelian group action are equivalent.Furthermore,we obtain that the topological entropy of a transitive,almost Banach-mean equicontinuous dynamical system of Abelian group action is zero.As an application of our main result,we show that the topological entropy of the Banach-mean equicontinuous system under the action of an Abelian groups is zero.
Key words Abelian group action;Banach mean equicontinuous;Banach mean density;independence set
1 Introduction
Ergodic theory and topological dynamics are two branches of the modern theory of dynamical systems.The first,though not in its broadest definition,deals with group actions on a probability measure space in a measure-preserving way;the second deals with the action of groups on a compact metric space as groups of homeomorphisms.In this paper,we discuss problems that exist under the framework of countable group action on the compact metric spaces which constitute the fundamental objects of study in the field of dynamical systems.
It is well known that equicontinuous systems have simple dynamical behaviors.A dynamical system is called equicontinuous if the collection of maps defined by the action of the group is a uniformly equicontinuous family.Equicontinuous systems are dynamically the‘simplest’ones;in fact,there is a complete classification of equicontinuous minimal systems.
Mean equicontinuity has attracted interest in recent years due to its connections with the ergodic properties of measurable dynamical systems,i.e.dynamical systems equipped with an invariant probability measure.In particular,it has been shown that using a measure theoretic version of mean equicontinuity,one can characterize when a measure-preserving system has a discrete spectrum[12]and when the maximal equicontinuous factor is actually an isomorphism[5,17].
The concept of mean equicontinuity comes in two variants:one is called Weyl-mean equicontinuity and the other Besicovitch-mean equicontinuity.The concepts of Weyl-and Besi-covitchmean equicontinuity were introduced in[17]for Z-actions.In fact,in this case the notion of Besicovich-mean equicontinuity is immediately seen to be equivalent to the concept of mean Lyapunov-stability,which was already introduced in 1951 by Fomin[9]in the context of Zactions with a discrete spectrum.Later,a first systematic treatment was carried out by Auslander[1].
Answering an open question in[24],it was proved by Li,Tu and Ye in[17]that every invariant measure of a mean equicontinuous system of integer group action has a discrete spectrum.Localizing the notion of mean equicontinuity,they introduced notions of almost mean equicontinuity and almost Weyl-mean equicontinuity.In[17]they proved that a system with the former property may have positive entropy while a system with the latter property must have zero entropy.
Concerning abelian group action,mean equicontinuity and its relation to the spectral theory of dynamical systems (in particular,to discrete spectrum) has been studied by various groups[11–13].In the minimal case and as regards the action of the Abelian group,Fuhrmann,Grger and Lenz[11]concluded that mean equicontinuity is equivalent to a discrete spectrum with continuous eigenfunctions.
Inspired by these previous papers,we will discuss the dynamical properties of countable Abelian group action systems.In this paper,we introduce the concept of Banach-mean equicontinuity regarding group action dynamical systems;this is broader than Weyl-and Besicovitchmean equicontinuity,and not limited to the dynamical systems of amenable group actions.Moreover,we prove that the above three concepts are equivalent when the dynamic system is an Abelian group action.Furthermore,we introduce the concept of almost Banach-mean equicontinuity for a countable Abelian group action system and obtain the following main result:
Theorem 1.1LetGbe a countably in finite Abelian group,letXbe a compact metric space without isolated points,and let the actionGXbe transitive.If the actionGXis almost Banach-mean equicontinuous,then
As an application of our main result,we prove that the topological entropy of the Banachmean equicontinuous system under the action of an Abelian groups is zero.
Theorem 1.2LetGbe a countably in finite Abelian group,letXbe a compact metric space,and letGXbe a continuous action.IfGXis Banach-mean equicontinuous,then

The paper is organized as follows:we begin in Section 2 by recalling some basic notations,definitions and results regarding group action systems.In Section 3 we relate the concept and basic propositions of the amenable group.Section 4 is devoted to the concepts of Banach-,Besicovitch-and Weyl-mean equicontinuity for amenable group actions.In this section we prove that the three concepts are equivalent when the dynamic system is an Abelian group action system.In Section 5 we introduce the concept of the Wely-mean sensitivity of an amenable group action system.In this section,we obtain a dichotomy result related to Wely-mean equicontinuity and Weyl-mean sensitivity for when a dynamical system is transitive.In Section 6,we give the proof of our main results.Finally,in Section 7,we apply our main result to prove the topological entropy of the Banach-mean equicontinuous system under the action of an Abelian group is zero.
2 Preliminaries
In this section,we recall some basic notations,definitions,and results.We refer the reader to the textbook[21]for information on group action.
By referring to an action of the groupGwith identityeon a setX,we mean a mapα:G×X→Xsuch that,writing the first argument as a subscript,αs(αt(x))=αst(x) andαe(x)=xfor allx∈Xands,t∈G.Most of the time we will write the action aswith the image of a pair (s,x) written assx.For a setA⊆Xands∈Gandx∈,Xwe write

TheG-orbit of a pointx∈Xis the setGx.
In this paper,we call a topological spaceXequipped with a continuous actionGXthe group action system,and denote it by (X,G).
Definition 2.1The actionGXis (topologically) transitive if,for all nonempty open setsU,V⊂X,there exists ans∈Gsuch thatsU∩VØ.The pointx∈Xis transitive ifDenote by Tran (X,G) the set of all transitive points.
The following proposition in[21]suggested that,whenXis metrizable,transitivity can be thought of as a generic version of minimality in the sense of a Baire category:
Proposition 2.2([21,Proposition 7.9]) Suppose thatXis metrizable.Then the following are equivalent:
1.the actionGXis transitive;
2.there is a dense orbit;
3.the set of points inXwith dense orbit is a denseGδ.
Definition 2.3A pointx∈Xis recurrent if for every neighbourhoodUofx,the set{s∈G:sx∈U}is in finite.Denote by Re (X,G) the set of all recurrent points.
Proposition 2.4([21,Proposition 7.11]) Suppose that the actionGXis transitive and thatXis metrizable and has no isolated points.Then the set of recurrent points inXis a denseGδ.
Definition 2.5LetXbe a set.A collection{(Ai,1,...,Ai,k):i∈I}ofk-tuples of subsets ofXis said to be independent iffor every nonempty finite setF⊆Iandω∈{1,...,k}F.
Definition 2.6LetGXbe an action and A=(A1,...,Ak) a tuple of subsets ofX.We say that a setJ⊆Gis an independence set for A if the collection{(s-1A1,...,s-1Ak):s∈J}is independent.
Definition 2.7LetGbe a group.Denote by Fin (G) the family of all non-empty finite subsets ofG.LetE⊆Gbe a subset ofG.The upper Banach density ofEis defined as
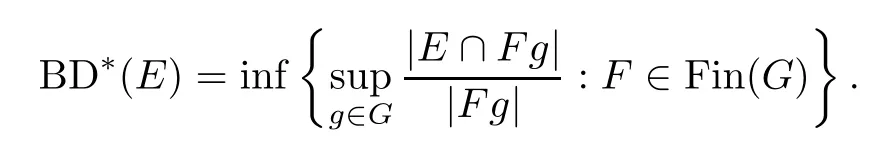
The lower Banach density ofEis given by BD*(E)=1-BD*(GE).
Clearly one has BD*(E)≤BD*(E).If BD*(E)=BD*(E),then we say that there exists the Banach density ofEand denote it by BD (E).
From the above definitions it is easy to see that the Banach upper density has a right shift invariant property.For the sake of completeness,we give a proof here.
Proposition 2.8BD*(Es)=BD*(E) for anys∈GandEsubset of G.
ProofBy the symmetry of the pair of setsEsandE,it is sufficient to prove that BD*(Es)≤BD*(E).LetFbe any nonempty finite subset ofG.From the definition of the Banach upper density ofEs,one has

The arbitrariness ofFimplies that BD*(Es)≤BD*(E).Hence the proposition is obtained.□
It is not difficult to observe the following result:
Lemma 2.9LetF,F1,F2be subsets ofGands∈G.Then,
1.ifF1has a Banach density of one andF1⊆F2,then so doseF2;
2.ifFhas a Banach density of one,thenGFis a set of Banach density zero;
3.ifF1andF2have a Banach density of one,then so doesF1∩F2;
4.ifFhas a Banach density of one,then so doesFs.
3 Amenable Group
This section is devoted to the class of amenable groups.This is a class of groups that plays an important role in many areas of mathematics,such as ergodic theory,harmonic analysis,dynamical systems,geometric group theory,probability theory and statistics.
LetGbe a group.A mean for G onℓ∞(G) is a unital positive linear functionσ:ℓ∞(G)→C (unital means thatσ(1)=1).The meanσis left invariant ifσ(sf)=σ(f) for alls∈Gandf∈ℓ∞(G),where (sf)(t)=f(s-1t) for allt∈G.
Definition 3.1The groupGis said to be amenable if there is a left invariant mean onℓ∞(G).
The above definition of a countable amenable groupGis equivalent to the existence of a sequence of finite subsets{Fn}ofGwhich is asymptotically invariant,i.e.,
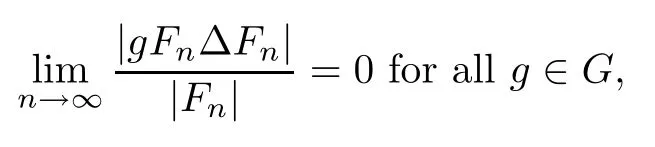
wheregFn={gf:f∈Fn},|·|denotes the cardinality of a set,and Δ is the symmetric difference.Such a sequence is called a (left) Følner sequence.
The class of amenable groups contains,in particular,all finite groups,all Abelian groups and,more generally,all solvable groups.In this paper,we need the following theorem:
Theorem 3.2([6,Theorem 4.6.1]) Every Abelian group is amenable.
Definition 3.3LetFandAbe nonempty finite subsets ofG.We say thatAis (F,ε)-invariant if|s∈A:Fs⊆A|≥(1-ε)|A|.
Definition 3.4Letfbe a real-valued function on the set of all finite subsets ofG.We say thatf(A) converges to a limitLasAbecomes more and more invariant if,for everyε>0,there are a finite setF⊆Gand aδ>0 such that|f(A)-L|<εfor every nonempty (F,δ)-invariant finite setA⊆G.
Theorem 3.5([21,Theorem 4.38]) Suppose thatGis amenable.Letφbe a[0,∞)-valued function on the set of all finite subsets ofGsuch that
1.φ(As)=φ(A) for all finiteA⊆Gands∈G;
2.φ(A∪B)≤φ(A)+φ(B) for all finiteA,B⊆G(subadditivity).Thenφ(A)/|A|converges to a limit asAbecomes more and more invariant.
LetGXbe an action and A=(A1,...,Ak) a tuple of subsets ofX.It is readily seen that the function

on the collection of nonempty finite subsets ofGsatisfies the two conditions in Theorem 3.5,so that the quantityφA(F)/|F|converges asFbecomes more and more invariant (Definition 3.4),and the limit is equal to infFφA(F)/|F|whereFranges over all nonempty finite subsets ofG.
Definition 3.6For a finite tuple A=(A1,...,Ak) of subsets ofX,we define the independence densityI(A) of A to be the above limit.
Proposition 3.7([21,Proposition 12.7]) Let A=(A1,...,Ak) be a tuple of subsets ofXand letd>0.Then the following are equivalent:
1.I(A)≥d;
2.there are a Følner sequence{Fn}and an independence setJfor A such that

In what follows,we recall some notions which were introduced in[20].
LetE⊆G.The upper asymptotic density ofEwith respect to a Følner sequence F={Fn}n∈N,denoted by(E),is defined by
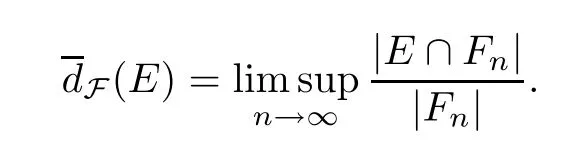
Similarly,the lower asymptotic density ofEwith respect to a Følner sequence F={Fn}n∈N,denoted by(E),is defined by
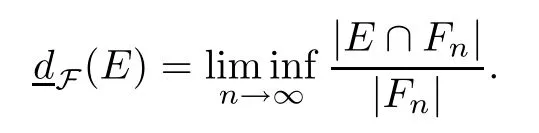
One may say thatEhas an asymptotic densitydF(E) ofEwith respect to a Følner sequence,wheredF(E) is equal to this common value.
Let{Fn}n∈Nbe a Følner sequence of the amenable groupGandE⊆G.For the upper Banach density ofEplease refer to Definition 2.7.Meanwhile,we have the following formula for the properties of upper Banach density (see[8,Lemma 2.9]):

As for the relationship between upper Banach density and upper asymptotic density,we have the following formula (see[4,Lemma 3.3]):

Here the supremum is taken over all Følner sequences F={Fn}n∈NofG.
Throughout this paper,Gis a countable amenable group andGXis a continuous action on a compact metric space.We write△k(X) for the diagonal{(x,...,x):x∈X}inXk.
Definition 3.8We call a tuplex=(x1,...,xk)∈Xkan IE-tuple (or IE-pair ifk=2) if,for every product neighbourhoodU1×...×Ukofx,the tuple (U1,...Uk) has positive independence density.We denote the set of IE-tuples of lengthkby IEk(X,G).
In this paper,we need the following theorem:
Theorem 3.9([21,Theorem 12.19]) IE2(X,G)Δ2(X) is nonempty if and only ifhtop(X,G)>0.
4 Besicovitch-,Weyl-and Banach-Mean Equicontinuity
In a 2005 study of a dynamical system with bounded complexity (defined by using the mean metrics),Huang,Li,Thouvenot,Xu and Ye[18]introduced a notion called“equicontinuity in the mean”.In 2015,Li,Tu and Ye[17]showed that for a minimal system,the notions of mean equicontinuity and equicontinuity in the mean are equivalent for Z-actions.The concepts of Besicovitch-and Weyl-mean equicontinuity were introduce,in[17]for Z-actions,and in[11]for amenable actions.
In this paper,we give a notion of Banach-mean equicontinuity on a dynamical system for a group action.For countable amenable group action systems,we show that two concepts,Weyland Banach-mean equicontinuity are equivalent.By the results of[11],we also know that the concepts of Besicovitch-,Weyl-and Banach-mean equicontinuity are the same for Abelian group action systems.
Definition 4.1LetGbe a discrete group and let Fin (G) be the family of all non-empty finite subsets ofG.LetXbe a compact metric space with metricd.Forx,y∈X,we denote

We say that the actionGXis Banach-mean equicontinuous or simply B-mean equicontinuous if,for anyε>0,there existsδ>0 such that(x,y)<εwheneverd(x,y)<δforx,y∈X.
A pointx∈Xis called a Banach-mean equicontinuous point if,for for every∈>0,there existsδ>0 such that,for everyy∈B(x,δ),

We say that the actionGXis almost Banach-mean equicontinuous if the group action system (X,G) has at least one Banach-mean equicontinuous point.
By the compactness ofX,it is easy to see that the actionGXis Banach-mean equicontinuous if and only if every point inXis a Banach-mean equicontinuous point.
Definition 4.2LetGbe an amenable group and F={Fn}n∈Nbe a Følner sequence ofG.We say that the actionGXis Besicovitch-F-mean equicontinuous if,for everyε>0,there existsδ>0 such that

for allx,y∈Xwithd(x,y)<δ.The dependence on the Følner sequence immediately motivates the next definition.We say that the actionGXis Weyl-mean equicontinuous if,for everyε>0,there existsδ>0 such that,for allx,y∈Xwithd(x,y)<δ,we have

A pointx∈Xis called a Weyl-mean equicontinuous point if,for for every∈>0,there existsδ>0 such that,for everyy∈B(x,δ),

We say that the actionGXis almost Weyl-mean equicontinuous if the group action system (X,G) has at least one Weyl-mean equicontinuous point.
Before we can proceed,a few comments are in order.First,note thatFandDare pseudometric.Moreover,as is not hard to see,DisG-invariant;that is,D(gx,gy)=D(x,y) for allx,y∈Xandg∈G.
In what follows,for the amenable group action system,we will see that the Banach pseudometric(·,·) is equal to the Wely pseudometricD(·,·).
Theorem 4.3LetGbe a countable amenable group,letXbe a compact metric space and letGXbe a group action.Then

ProofLetx,y∈X.First,we show that
Letε>0.From the definition of(x,y),there is a nonempty finite subsetF∈Fin (G) such that
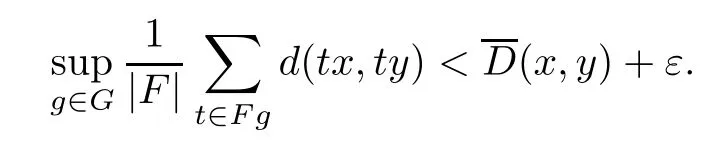
Let{Fn}n∈Nbe a Følner sequence ofG.In what follows we will show that

Takeg∈G.For everyh∈Fn,one has

Thus it follows that

We denote thatα(h,t)=d((thg)x,(thg)y) forh∈Fnandt∈F.Then the above inequality can be re-written as

It is clear that there ist′∈Fsuch that

Therefore,we get

which implies that

Note that

where diam (X) is the diameter of the compact metric space (X,d).SinceFnis a Følner sequence,we have that

From the arbitrariness of the Følner sequence{Fn},we get

where the supremum is taken over all Følner sequences ofG;that is
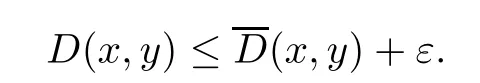
The arbitrariness ofεimplies that

Suppose thatD(x0,y0)(x0,y0) for somex0,y0∈X.In what follows,we will obtain a contradiction.
We choose two real numbersη1,η2∈R,such that

Let{Fn}n∈Nbe a Følner sequence of the amenable groupG.Note thatFnis a nonempty finite subset ofGfor eachn∈N.From the definition of(x0,y0),we have
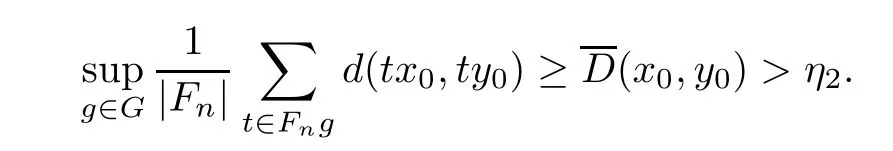
Thus,for eachn∈N,there existsgn∈Gsuch that

SetHn=Fngn.Since F′:={Hn}n∈Nis also a (left) Følner sequence ofG,we get that

This is a contradiction.Hence the theorem is proved. □
From the above Theorems,it follows that the concepts of Banach-and Weyl-mean equicontinuity are equivalent for the amenable group action system.
Corollary 4.4LetGbe a countable amenable group,letXbe a compact metric space let andGXbe a group action.ThenGXis Banach-mean equicontinuous if and only ifGXis Weyl-mean equicontinuous.
According to the theorem on the independence of Følner sequences for an amenable group in[11,Theorem 1.3,p.6],we can get the following result:
Theorem 4.5LetGbe a countable Abelian group andGXbe a dynamical system.Then the following three statements are equivalent:
1.GXis Banach-mean equicontinuous;
2.GXis Weyl-mean equicontinuous;
3.GXis Besicovitch-F-mean equicontinuous for some left Følner sequence F.
LetGbe a countable amenable group and letGXbe a group action.Let E denote the set of all Weyl-mean equicontinuous points of the group action system (X,G).For everyε>0,let

For the Weyl-mean equicontinuous points we have the following proposition:
Proposition 4.6LetGbe a countable amenable group,letGXbe a group actionand letε>0.Then Eεis open andsEε/2⊆Eεfor alls∈G.Moreover,is aGδsubset ofX.
ProofLetx∈Eε.Chooseδ>0 satisfying the condition from the definition of Eεforx.Fixy∈B(x,δ/2).Ifz,w∈B(y,δ/2),thenz,w∈B(x,δ),soD(z,w)<ε.This shows thatB(x,δ/2)⊆Eε,and hence,Eεis open.
Lets∈G.Suppose thatx∈sEε/2,sos-1x∈Eε/2.Chooseδ>0 satisfying the condition from the definition of Eε/2fors-1x;that is,for ally,z∈B(s-1x,δ),one hasD(y,z)<ε/2.By the continuity of the maps-1,there existsη>0 such thatd(s-1y,s-1x)<δfor anyy∈B(x,η).
Letu,v∈B(x,η).Thens-1u,s-1v∈B(s-1x,δ).
Let F={Fn}n∈Nbe any Følner sequence ofG.Note that Fs={Fns}n∈Nis also a (left) Følner sequence ofG.Thus,we have

The arbitrariness of the Følner sequence F indicates thatD(u,v)≤ε/2<ε,which implies thatx∈Eε.Hence we getsEε/2⊆Eε.
Ifx∈Xbelongs to all E,then clearly,x∈E.
Conversely,ifx∈E andm≥1,there existsδ>0 such thatD(x,y)<1/2mfor ally∈B(x,δ).Ify,z∈B(x,δ),then

Thusx∈.Therefore we get.Hence,the proof is completed. □
5 Weyl-Mean Sensitivity
LetXbe a compact metric space.Recall that a subset ofXis called residual if it contains the intersection of a countable collection of dense open sets.By the Baire category theorem,a residual set is also dense inX.
Definition 5.1LetGXbe a continuous action and letx∈Xbe a point.We say that the pointxis a Weyl-mean sensitive point if there existsδ>0 such that,for everyε>0,there isy∈B(x,ε) satisfying

For the definition of the functionD(·,·),please refer to (4.1).
We say that the actionGXis Weyl-mean sensitive if every pointx∈Xis a Weyl-mean sensitive point.
Proposition 5.2LetGbe a countable amenable group and letXbe a compact metric space.LetGXbe a transitive action.Then,
1.The set of Weyl-mean equicontinuous points is either empty or residual.If,in addition,the actionGXis almost Weyl-mean equicontinuous,then every transitive point is Weylmean equicontinuous.
2.If the actionGXis minimal and almost Weyl-mean equicontinuous,then it is Weyl-mean equicontinuous.
ProofIf Eεis empty for someε>0,then the set of Weyl-mean equicontinuous points E is empty.
Now,we assume that every Eεis nonempty.Then,for eachε>0,Eεis a nonempty open subset ofX.In what follows we show that every Eεis dense.LetUbe any nonempty open subset ofX.By the transitivity of the actionGX,noting that Eε/2is a nonempty open subset ofXand considering Proposition 4.6,there existss∈Gsuch that ØU∩sEε/2⊆U∩Eε.
Hence E is either empty or residual,by the Baire Category Theorem.
If E is residual,then every Eεis open and dense.Letx∈Xbe a transitive point andε>0.Then there exists some elements∈Gsuch thatsx∈Eε/2,and,by Proposition 4.6,x∈s-1Eε/2⊆Eε.Thusx∈E. □
Proposition 5.3LetGbe a countable amenable group and letXbe a compact metric space.LetGXbe a continuous action.If there existsδ>0 such that for every non-empty open subsetUofXthere arex,y∈UsatisfyingD(x,y)>δ,Then the group actionGXis Weyl-mean sensitive.
ProofSuppose that there existsδ>0 such that for any nonempty open subsetUofX,there areu,v∈UsatisfyingD(u,v)>δ.
Letx∈Xandε>0.ThenB(x,ε)Ø andB(x,ε) is open subset ofX.Then there existy,z∈B(x,ε)⊆XsatisfyingD(y,z)>δ.
Proposition 5.4LetGbe a countable amenable group and letXbe a compact metric space.Let the actionGXbe transitive.If there exists a transitive point which is a Weyl-mean sensitive point,then the actionGXis Weyl-mean sensitive.
ProofLetx∈Xbe a Weyl-mean sensitivity point.Thus there existsδ>0 such that,for everyε>0,there isy∈B(x,ε) satisfyingD(x,y)>δ.
Take a nonempty open subsetUofX.Sincexis a transitive point,there existss∈Gsuch thatsx∈U;that is,x∈s-1U.Furthermore,ass-1Uis open,there is∈>0 such thatB(x,∈)⊆s-1U;that is,sB(x,∈)⊆U.By the assumption thatxis a Weyl-mean sensitivity point,there existsy∈B(x,∈) satisfying thatD(x,y)>δ.By the definition ofD(x,y),there is a (left) Følner sequence F={Fn}n∈NofGsuch thatDF(x,y)>δ.
Letu=sx,v=sy.Noting that Fs-1={Fns-1}n∈Nis also a (left) Følner sequence andu,v∈U,then

Therefore the actionGXis Weyl-mean sensitive,by Proposition 5.3. □
Theorem 5.5LetGbe a countable amenable group and letXbe a compact metric space.If the actionGXis transitive,then the actionGXis either almost Weyl-mean equicontinuous or Weyl-mean sensitive.
ProofLetx∈Xbe a transitive point.Ifxis a Weyl-mean sensitivity point,then the actionGXis Weyl-mean sensitive,by Proposition 5.4.Ifxis not a Weyl-mean sensitive point,then it is a Weyl-mean equicontinuous point.Thus the actionGXis almost Weylmean equicontinuous. □
Corollary 5.6LetGbe a countable amenable group and letXbe a compact metric space.LetGXbe a minimal system.Then the actionGXis either Weyl-mean sensitive or Weyl-mean equicontinuous.
6 The Proof of Main Theorem
To prove our main theorem we need some preparation.For the following result,please see[17,Proposition 5.8]:
Proposition 6.1Let (X,β,μ) be a probability space,and letbe a sequence of measurable sets withμ(Ei)≥a>0 for some constantaand anyi∈N.Then,for anyk≥1 and∈>0,there isN=N(a,k,∈) such that,for any tuple{s1<s2<...<sn}withn≥N,there exist 1≤t1<...<tk≤nwith

Let (X,d) be a compact metric space,with Borelσ-algebra B.Denote by M (X) the space of Borel probability measures onX.Our main interest is the weak-*topology of space M (X).This is standard (see Pathasarathy[22]).
Theorem 6.2LetXbe compact metric space and let{μn}be a sequence of probability measures in M (X).Letμ∈M (X).Then the following statements are equivalent:
1.{μn}converges toμwith weak-*topology in M (X);
In order to obtain our results,we need the following fundamental fact:
Fact 6.3Let{an}and{bn}be two sequences of real numbers.Suppose thatexists and thatis finite.Then

The next result is the well-known Furstenberg corresponding principle[10]of the amenable group version.
Proposition 6.4LetGbe a countable amenable group and letFbe a subset ofGwith BD*(F)>0.Then for anyk≥1 and∈>0,there isN=N(BD*(F),k,∈) such that,for anyn≥Nand any tuple{s1,s2,...,sn}⊆G,there exist{1≤t1<t2<...<tk≤n}such that
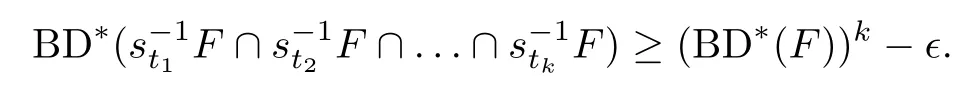
ProofLetK={0,1}be a finite alphabet.We define the map Σ:G×KG→KGby Σ(g,x):=x°Rgfor allg∈G andx∈KG.HereRg:G→Gis defined byRg(h):=hgfor allh∈G.Lets∈Gandx∈KG.Thussx(g)=x(gs) for allg∈G.
Takeξ∈KGsatisfyingξ(s)=0 for alls∈Fandξ(s)=1 for alls∈GF.Denote by
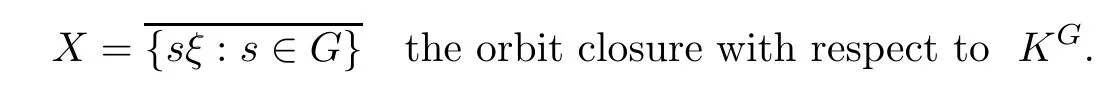
It is clear thatXis a compact metric space.Meanwhile,it follows that the set{s∈G:ξ(s)=0}=Fhas positive upper Banach density.
Let{Hn}be a (left) Følner sequence forG.By a formula of upper Banach density (see[8,Lemma 2.9]),we have that

Letκ>0.For the above limit equation,there isN1∈N such that,for everyn≥N1,one has that

Thus,for eachn≥N1,there isgn∈Gsuch that

SetFn=Hngnfor alln∈N.Then{Fn}n∈Nis a (left) Følner sequence with

Define a sequence of probability measures in M (X) as
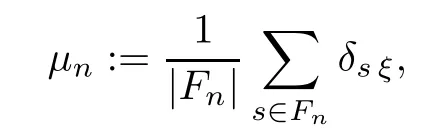
whereδsξis Dirac measure at the pointsξinX.
Since M (X) is a compact metrizable space (see Theorem 6.3 in[22],p43),there exists a subsequence{μnl}l∈Nthat converges to a probability measureνwith weak-*topology in M (X);that is,
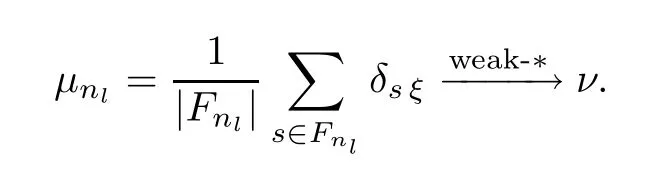
In what follows we will show thatνis aG-invariant probability measure;that is,ν=gνfor eachg∈G.
Letg∈G.From (3) of Theorem 6.2,it is easy to check that

ClaimFor any Borel setBofX,one has that

In fact,since{Fnl}l∈Nis a Følner sequence ofG,we have that


Hence the claim is obtained.
Now we will prove thatgν=ν.LetCbe any closed subset ofX.From (6.3),Fact 6.3 and (3) of Theorem 6.2,we have tnat

Applying (3) of Theorem 6.2 again,we getCombining this with (6.2),we have thatgν=ν.Thusνis aG-invariant measure.
Denote byethe unit element of the groupG.We defineA(0)={η∈KG:η(e)=0}∩X.Since{η∈KG:η(e)=0}is a clopen subset ofKG,it follows thatA(0) is a clopen subset ofX.Therefore the boundary ofA(0) is a empty set;that is,∂(A(0))=Ø.From (5) of Theorem 6.2,we have that

Note thatsξ∈A(0)⇔ξ(s)=0⇔s∈F,so,by (6.1),we get tnat
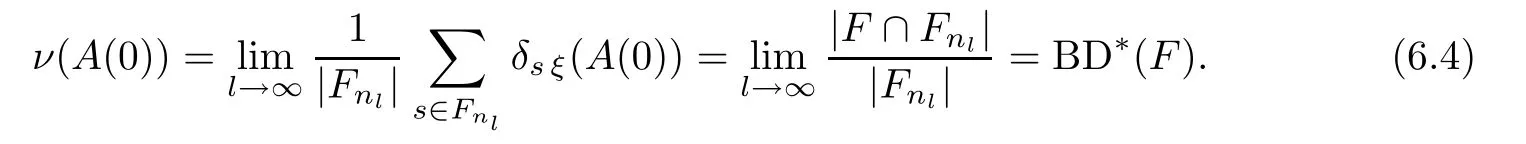
SinceGis countable,we listGasDenote thatA(0) for eachi∈N.Owing toνbeingG-invariant,we deduce that=ν(A(0))=BD*(F) for eachi∈N.
Letk≥1 and∈>0.From Proposition 6.1,there isN=N(BD*(F),k,∈) such that,for anyn≥Nand any tuple{s1,s2,...,sn}⊆G,there exist{1≤t1<t2<...<tk≤n}satisfying
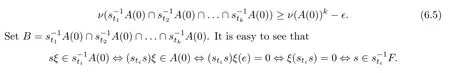
SinceA(0) is a clopen subset ofX,the setBis also clopen inX.Therefore,the boundary ofBis an empty set;that is,∂(B)=Ø.Thus,by equation (3.1) and (5) of Theorem 6.2,we have
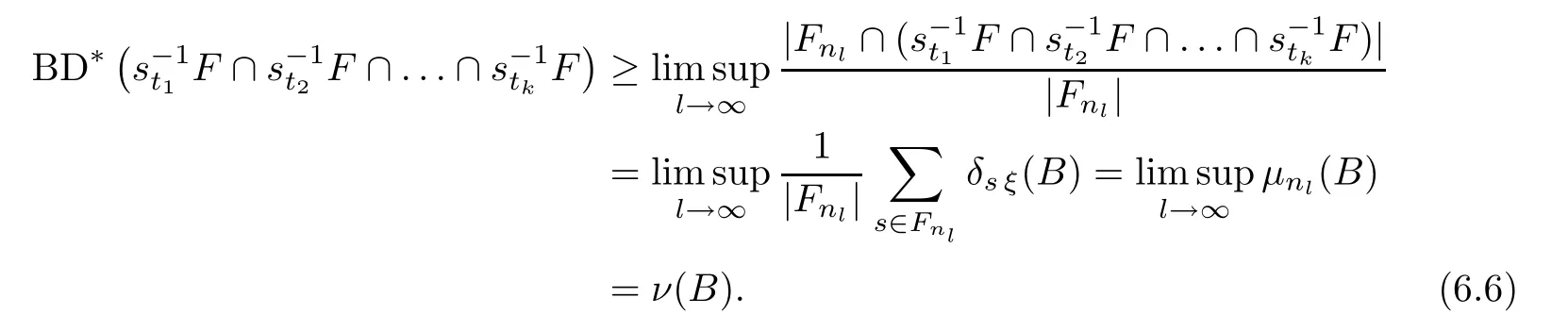
Applying (6.4),(6.5) and (6.6),we get

Hence the proposition is obtained. □
Lemma 6.5LetGbe a countably in finite amenable group,letSbe a subset ofGwith BD*(S)>0,and letW⊆Gbe an in finite set (i.e.|W|=∞).Then there are two distinct elementsl1,l2∈Wsuch that

as in Proposition 6.4,for the tuple{s1,s2,...,sn}⊆Wwithn≥N,there exist 1≤t1<t2≤nsuch that
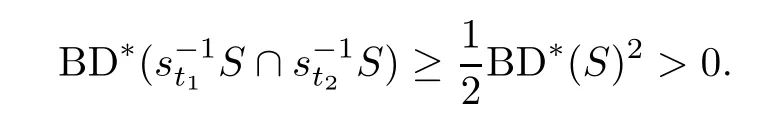
Letl1=st1andl2=st2.Then the proof is completed. □
The main result in this section is
Theorem 6.6LetGbe a countably in finite Abelian group and letXbe a compact metric space without isolated points.Suppose that the actionGXis transitive.Ifhtop(X,G)>0,then the actionGXis Weyl-mean sensitive.
ProofIt suffices to prove that there exists a transitive pointx0which is not a Weyl-mean equicontinuous point,by Proposition 5.4.
AsGis Abelian,the groupGis an amenable group.Sincehtop(X,G)>0,and by Theorem 3.9 and Definition 3.8,there exists an IE pair (x1,x2)∈IE2(X,G)△2(X) satisfying,for any nonempty open neighborhoodV1×V2∋(x1,x2),that A′.=(V1,V2) has positive independent density,i.e.,
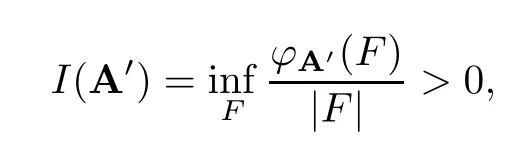
whereφA′(F)=max{|F∩J|:Jis an independent set for A′},andFranges over all nonempty finite subsets ofG.Sincex1x2,we choose two open setsUi(i=1,2) which are in the neighborhood ofxiwith
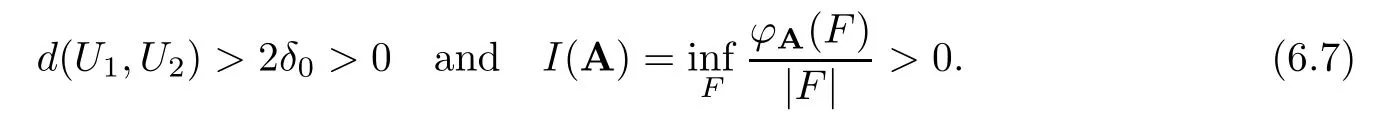
Here A=(U1,U2).Thus,by Proposition 3.7 and (3.1),there exists an independent setJfor A such that
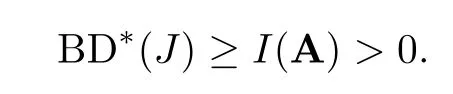
SinceGXis transitive andXhas no isolated points,by Propositions 2.2 and 2.4,we know that the set Tran (X,G) of points inXwith dense orbit and the set Re (X,G) of recurrent points are both denseGδsets ofX.Applying the Baire category theorem,we have that Tran (X,G)∩Re (X,G) is also a denseGδset ofX,which means that we have Tran (X,G)∩Re (X,G)Ø.
Letx0∈Tran (X,G)∩Re (X,G).In what follows,we will show thatx0is not a Weyl-mean equicontinuous point.
For eachδ>0,denote that

The cardinality of the setG(x0,B(x0,δ)) is in finite becausex0is a recurrent point.
Takem0∈N satisfying

Hereδ0is defined as in (6.7).Recall that,from (4.3),

The rest of the proof we will establish the following assertion:
Claimx0E1/m0.
Suppose that

Then there existsδ*>0 depending onx0andm0such that

Recall that BD*(J)>0 for the independent setJfor A.It follows from Lemma 6.5 that there are two distinct elements,

LetHbe a maximal subset ofwith the property that,for every pairg,s∈Handgs,φ(g)∩φ(s)=Ø(Zorn’s Lemma guarantees the existence of the setH).Now we claim that
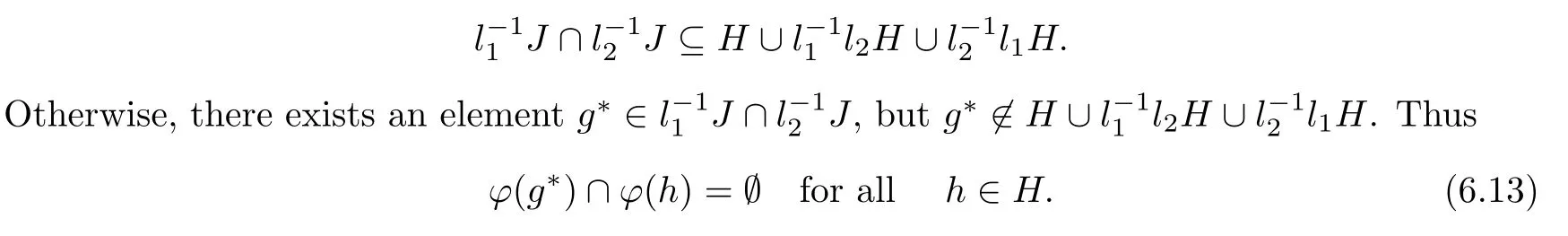
Indeed,ifφ(g*)∩φ(h0)Ø for someh0∈H,then,by the above argument,we know thatwhich contradicts the fact thatHence,by (6.13),we deduce that the setH∪{g*}satisfies the property that,for every pairg,s∈H∪{g*}andgs,φ(g)∩φ(s)=Ø.Noting thatg*Handwe can see that this contradicts the fact that the setHis a maximal subsetwith such a property.
Hence,we get

According to Proposition 2.8 and the fact thatGis abelian,one has that

Combining this with (6.14),it follows that

Therefore,we have

Recall thatGis an amenable group asGis abelian and Theorem 3.2.By (3.1),we know that

where the supremum is taken over all Følner sequences F={Fn}n∈NofG.Thus,by (6.15) and (6.16),there is a Følner sequence{Fn}ofGsatisfying
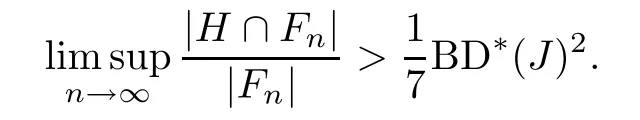
Therefore,there exists a subsequenceof N such thatmn<mn+1,mn≥nand

We denote thatJ1=l1Hand thatJ2=l2H.Sincewe immediately haveJ1∪J2⊆J.Furthermore,we have thatJ1∩J2=Ø.Indeed,ifJ1∩J2Ø,then there areh1,h2∈Hsuch thatl1h1=l2h2.Asl1l2,it follows thath1h2.Note that

Thusφ(h1)∩φ(h2)Ø andh1h2∈H,which contradicts the definition ofH.Hence,J1∩J2=Ø.
Letn∈N.Inequality (6.17) implies thatFmn∩HØ.Denote that
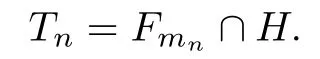
Then we define the mapsψi:Tn→Ji(i=1,2) as follows:

It is easy to see that

From the definition of the independent set ofJfor A=(U1,U2)(see Definition 2.5 and Definition 2.6),we get that
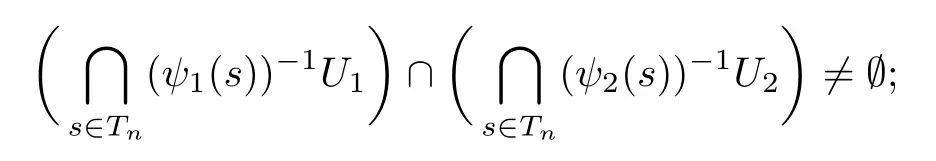

Moreover,for eachg∈Tn,sinceGis abelian,one has that

Combining this with 6.18 and withGbeing an Abelian group,we get that

Therefore,we obtain that,for eachg∈Tn,
Recall thatd(U1,U2)>2δ0.Hence,one has

Therefore,we have
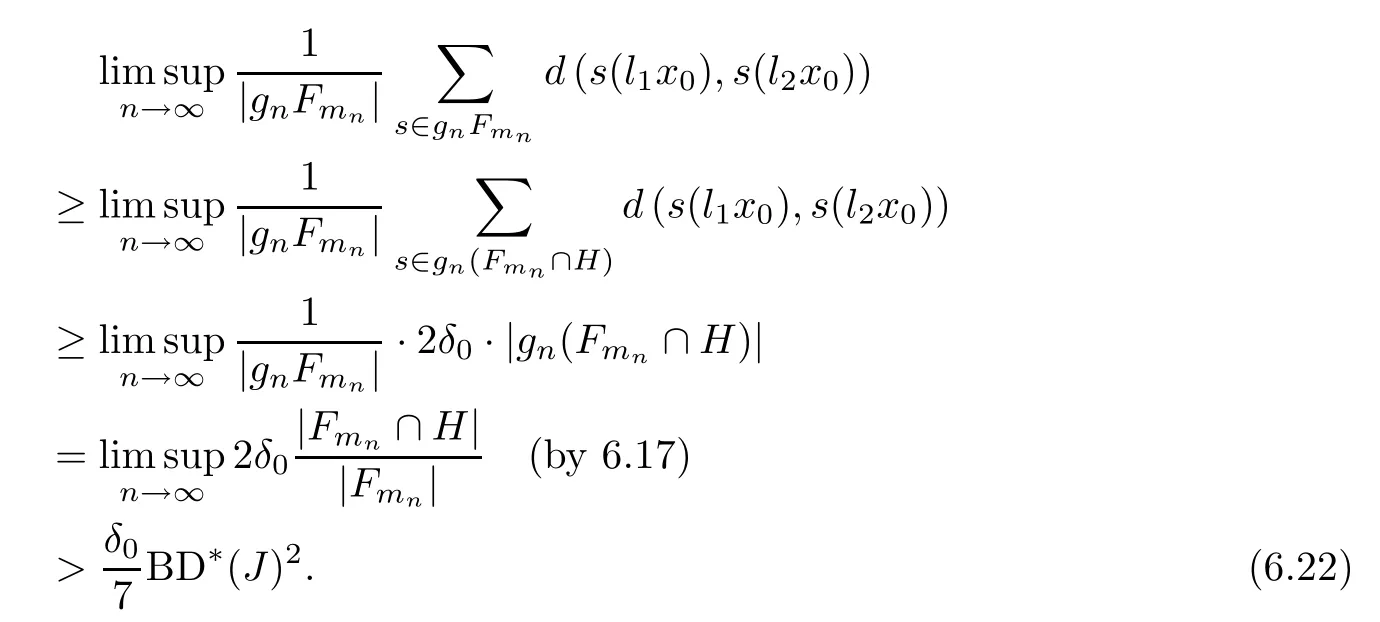
Denote that

Since{Fn}n∈Nis a Følner sequence of the Abelian groupG,F′is also a Følner sequence ofG.Inequality (6.22) shows that

Meanwhile,the above inequality implies thatl1x0l2x0.
Recall that,from (6.12) and (6.11),

This contradicts inequality (6.10).Hence we obtain that

Recall that E denotes the set of all Weyl-mean equicontinuous points of the group action system (X,G).From Proposition 4.6,we know that

By (6.25) and (6.26),we get

Therefore,x0is not a Weyl-mean equicontinuous point ofGX.Therefore,x0is a Weylmean sensitive point ofGX.By the assumption thatGXis transitive and Proposition 5.4,we deduce thatGXis Weyl-mean sensitive.
Hence,the theorem is proved. □
Proof of Theorem 1.1The proof follows from Theorem 6.6,Theorem 5.5,Theorem 3.2 and Theorem 4.3. □
7 An Application
In order to get our result,we need to establish the following concepts and theorems:
Definition 7.1([21]) By a p.m.p.(probability-measure-preserving) action ofG,we mean an action ofGon a standard probability space (X,μ) by measure-preserving transformations.In this case,we will combine the notation and simply writeG(X,μ).
Given an actionGXon a compact metric spaceX,we say that a setA⊆XisGinvariant ifGA=A,which is equivalent toGA⊆A.When the action is probability-measure preserving andAis a measurable set,we interpretG-invariance to mean thatGA=Amodulo a null set,i.e.,μ(sA△A)=0 for alls∈G.
Definition 7.2([21]) The actionG(X,μ) is said to be ergodic ifμ(A)=0 or 1 for everyG-invariant measurable setA⊆X.
Any dynamical system with an amenable group action admits invariant probability measures and the ergodic measures can be shown to be the extremal points of the set of invariant probability measures (see,for example,the monographs[7,25]).Let M (X),MG(X) and M(X) denote the sets of all Borel probability measures onX,theG-invariant regular Borel probability measures onX,and the ergodic measures in MG(X),respectively.
Proposition 7.3([21,Proposition 2.5]) For a p.m.p.actionG(X,μ),the following are equivalent:
1.the action is ergodic;
2.μ(A)=0 or 1 for every measurable setA⊆XsatisfyingsA=Afor alls∈G(i.e.,G-invariance in the strict sense);
3.for all setsA,B⊆Xof positive measure,there is ans∈Gsuch thatμ(sA∩B)>0.
Now,we recall the concept of amenable measure entropy (see[16]and[21]).
LetGbe a amenable group and letG(X,μ) be a p.m.p.action.Let
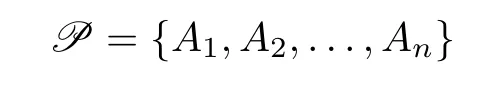
be a finite partition ofXand letFbe a nonempty finite subset ofG.Setting PFfor the join

whereFranges over nonempty finite subsets ofGand

The entropy of the actionG(X,μ) is

where P ranges over all finite partitions ofX.
The support of a measureμ∈M (X),denoted by supp (μ),is the smallest closed subsetCofXsuch thatμ(C)=1(see[23]);that is,

The following fact is well known:
Fact 7.4We have that

Topological entropy is related to measure entropy by the variational principle which asserts that for a continuous map on a compact metric space,the topological entropy equals the supremum of the measure entropy taken over all the invariant probability measures.The following is a statement of the variational principle of the version of the amenable group action that we need in this paper:
Theorem 7.5([19,Theorem 5.2]) (Variational principle of topological entropy) LetGbe an amenable group and letXbe a compact metric space.Then

As an application of our main result,we have
Theorem 7.6LetGbe a countable Abelian group,letXbe a compact metric space,and letGXbe a continuous action.IfGXis Banach-mean equicontinuous,then

ProofLetμbe an ergodic invariant measure on the actionGX.Denote byX0=supp (μ) the support of the ergodic invariant measureμ.It is clear thatX0is aG-invariant closed subset ofXand thatG(X0,μ) is also ergodic.Moreover,we have thathμ(X,G)=hμ(X0,G).
In what follows we show thathμ(X0,G)=0.
LetU,Vbe any pair nonempty open sets ofX0.Thenμ(U)μ(V)>0,on account of supp (μ)=X0and Fact 7.4.Thus there is an elements∈Gsuch thatμ(U∩sV)>0 on account ofG(X0,μ) being ergodic and Proposition 7.3;that is,

Note thatX0is a compact metric space.Hence the actionGX0is topological transitive.
Now we divide things into two cases to complete our proof.
Case 1X0has no isolated points.
SinceGXis Banach-mean equicontinuous,it is clear thatGX0is also Banach-mean equicontinuous.By Theorem 1.1 and becauseX0has no isolated points,we get that

Note thatμ|X0is an ergodic measure ofGX0.Then,by Theorem 7.5,we obtain that
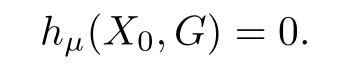
Therefore,we have that

Recall thatμbe any ergodic invariant measure on the actionGX.Again applying Theorem 7.5,we deduce that

Case 2X0has isolated points.
Suppose thatx0∈X0is an isolated point ofX0,so the single point set{x0}is an open set ofX0.LetV⊆X0be any open set.Since the actionGX0is topological transitive,there iss∈Gsuch thatsx0∈V.This fact implies that the orbit ofx0is dense inX0;that is,
Note thatx0∈supp (μ) and that the single point set{x0}is an open set.Thus one hasμ({x0})>0.Sinceμ(X0)=1,we deduce that the cardinality of the setGx0is finite (i.e.,|Gx0|<∞).Combining this withwe get that the cardinality of the spaceX0is finite (i.e.,|X0|<∞).By the definition of topological entropy,it is easy to see that

In what follows,with an argument similar to that in Case 1,we can obtain that

Hence the theorem is proved. □
AcknowledgementsThe authors are very grateful to Prof.Hanfeng Li and Prof.Jian Li for their generous sharing of knowledge about the topic.
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- A ROBUST COLOR EDGE DETECTION ALGORITHM BASED ON THE QUATERNION HARDY FILTER*
- CONTINUOUS SELECTIONS OF THE SET-VALUED METRIC GENERALIZED INVERSE IN 2-STRICTLY CONVEX BANACH SPACES*
- EXISTENCE RESULTS FOR SINGULAR FRACTIONAL p-KIRCHHOFF PROBLEMS*
- BOUNDS FOR MULTILINEAR OPERATORS UNDER AN INTEGRAL TYPE CONDITION ON MORREY SPACES*
- LEARNING RATES OF KERNEL-BASED ROBUST CLASSIFICATION*
- A COMPACTNESS THEOREM FOR STABLE FLAT SL (2,C) CONNECTIONS ON 3-FOLDS*
