基于辅助信标的无人机协同目标跟踪

史浩然, 卢发兴, 祁江鑫, 杨 光

(海军工程大学兵器工程学院, 湖北 武汉 430033)

0 引 言

相比较传统武器而言,超高速炮在反应速度、攻击射程以及可控性等方面表现出明显的优势,但如何为超高速炮提供精确的超视距目标指示是亟需解决的关键问题。现有的超视距目标指示手段包括卫星侦察、预警机侦查、前哨侦查等,然而卫星侦查手段实时性、动态性难以满足要求,预警机侦查主要用于保障反舰导弹武器。无人机由于具有较强的机动性能,而且隐身性能好、成本低,因此广泛应用于目标侦察领域。

许多文献都对基于无人机的目标定位与跟踪进行了广泛的研究。邵慧等研究了影响无人机精确定位的因素,其中主要影响因素包括无人机位置、姿态角的导航精度以及无人机和目标之间的相对位置关系,而在现有的导航系统中缺乏较为成熟的对无人机姿态直接进行测量的系统,姿态角的可观测性较差,存在较大的姿态角误差。在无人机姿态估计方面,大多数的姿态估计算法是基于卡尔曼滤波及其衍生形式。文献[2]采用扩展卡尔曼滤波(extended Kalman filter, EKF)提高姿态估计的精度。Garcia等采用无迹卡尔曼滤波(unscented Kalman filter, UKF)得到小型航天器的位姿估计。蔡安江等提出一种基于四元数衍生UKF算法的多旋翼无人机姿态估计算法,但是这种基于融合滤波的方法难以建立合适的姿态方程以及确定噪声协方差。

影响定位精度的另一个重要因素是无人机和目标之间的相对位置关系,即通过研究多无人机位置配置以增强目标状态估计,通常以Fisher信息矩阵(Fisher information matrix, FIM)的行列式作为目标函数。Bishop等研究了仅方位信息、仅距离信息以及仅到达时间信息下多传感器几何配置问题。文献[9-10]研究了二维空间中基于测角测距的双机最优观测配置问题。Zhao等基于框架理论研究了二维和三维空间中传感器的最优观测构型,考虑了3种传感器:仅角度测量、仅范围测量和接收信号强度测量。如何保持双机甚至多机之间的观测配置获得最优的目标估计,这是多机协同定位跟踪的又一难点问题。文献[12]研究了通信和测量受限条件下的无人机分布式控制问题,文献[13]基于滚动时域控制的方式实现多机协同最优目标跟踪。Yao等受粒子群优化(particle swarm optimization, PSO)算法和微分进化(differential evolution, DE)算法思想的启发,提出了一种改进的灰狼优化算法,优化无人机的轨迹以延长对目标的跟踪时间。这种在线优化方法运算量大,实时性是需要解决的问题。Kim等提出了一种非线性模型预测控制框架用于双无人机的协同standoff跟踪,在模型预测控制方程中,使用罚函数处理无人机性能约束和机间的防碰撞。Song等提出一种针对运动目标的微分几何制导法实现对目标的standoff跟踪。Kokolakis等提出一种分布式稳健制导律实现standoff目标跟踪。但是以上方法只考虑了盘旋阶段使无人机保持最优观测,并未考虑趋近阶段的最优观测问题。Ousingsawat等基于FIM性能指标结合滚动时域方法求解无人机趋近目标的最优轨迹,同时考虑了风险区域和终端的限制条件。孙顺等针对趋近阶段和保持阶段的最优布站配置,通过闭环最优控制方法实现了到达时间差(time difference of arrival, TDOA)定位体制的多机轨迹优化。

无人机姿态角是影响无人机定位精确度的主要因素,目前针对无人机协同定位跟踪问题的研究并没有考虑到姿态角的影响。而且基于势场法的多机协同控制问题,并未考虑传感器观测精度、无人机与目标的距离对最优轨迹的影响。为此,本文提出一种基于辅助信标的多无人机协同跟踪定位算法,通过辅助信标校正无人机的姿态角,减小姿态角误差的影响。考虑最优轨迹的影响因素,设计一种双机趋近目标运动的优化控制方法,使双无人机保持在较好的观测位置,从而增加测量信息,减小目标状态估计的不确定度,提高准确性,以达到对超视距目标精确指示的目的。

1 基于辅助信标的无人机姿态校正模型

研究表明,影响无人机定位精度的因素主要包括无人机位置误差、无人机姿态误差以及无人机测量误差。由于测量误差与无人机探测设备有关,而且可以通过滤波算法减少测量误差的影响;通过设置辅助信标(辅助信标的位置精度相对较高),然后无人机测量出辅助信标与目标之间的相对位置,得到目标的精确位置,从而消除无人机位置误差的影响,因此提高无人机姿态角的导航精度可以有效提高目标的定位精度。本部分采用一种基于辅助信标的无人机姿态校正方法,提高目标的定位精度,基于辅助信标的无人机姿态校正概念图如图1所示。

图1 基于辅助信标的无人机姿态校正概念图Fig.1 ConceptFigure of attitude correction by the unmanned aerial vehicle based on aided beacon

1.1 坐标系及变换

绝对地理坐标系:原点固定在地面某一位置,面与地表相切,轴向东,轴向北,轴指向天顶。用下标表示。

载体地理坐标系:原点固定在无人机质心,坐标轴与绝对地理坐标系坐标轴平行。用下标表示。

载体坐标系:原点固定在无人机质心,轴指向无人机朝向,轴与轴垂直在无人机横截面内,轴垂直于面指向无人机上方。用下标表示。

(1)

式中：

(2)

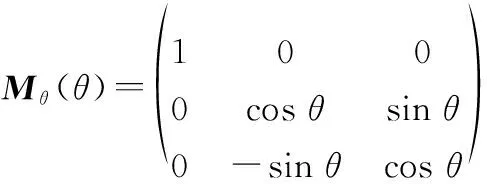
(3)

(4)

1.2 基于辅助信标的姿态校正

设绝对地理坐标系下,辅助信标位置为,,无人机对辅助信标的量测为(+Δ,+Δ,+Δ),其中、、分别表示无人机观测的距离、方位角和俯仰角信息,Δ、Δ、Δ为相对应的观测误差,则可得到辅助信标在无人机直角坐标系中的观测值为

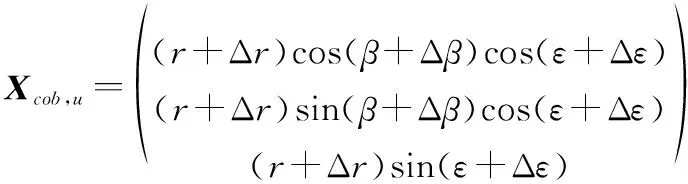
(5)

在理想情况下,应当有

(6)

然而,由于姿态角误差、观测误差与无人机位置误差的存在,式(6)并不成立,因此需要求解姿态角ϑ使下式最小：

(7)

式中：(ϑ)表示无人机观测辅助信标的位置与辅助信标真实位置之间的误差。

在式(7)中只有坐标变换矩阵(ϑ)未知,因此可以通过梯度下降法求解ϑ使min(ϑ)=(ϑ),以ϑ作为无人机姿态的校正值,在理论上具有比观测值ϑ更高的精度。

2 观测航迹优化

最优观测航迹是指使目标状态估计误差最小的无人机观测航迹,测量数据的质量与无人机相对目标的观测位置密切相关,不同的观测位置得到的测量数据所提供的目标信息是不同的。测量数据的“好”或“坏”,直接影响目标的状态估计,也影响后续的滤波处理与姿态校正。本部分的主要研究内容是实时规划无人机的轨迹,使无人机处于观测优化的位置,从而有效提高对目标的观测质量。

2.1 最优观测配置

误差协方差是状态估计常用的性能指标,它表示状态估计的不确定程度,因此误差协方差应尽可能小。克拉美罗下界(Cramer-Rao lower bound, CRLB)定义了理想情况下状态估计误差协方差所能达到的最低下界,而且CRLB与系统的固有属性有关,与具体估计算法无关,CRLB的数学表达式为

(8)

表示FIM,是CRLB的逆,表示在给定的观测值中所包含的有关状态参数的信息量。

det()为的矩阵行列式,与状态参数的不确定度成反比,因此,传感器最优观测即为det()的最大值。在三维空间中,双无人机对目标进行观测时,det()可以由下式计算得到：

(9)

式中：、分别为无人机观测距离标准差和角度标准差；、分别为无人机1和无人机2与目标之间的距离；为两架无人机与目标之间的视线夹角。具体证明过程见文献[24]。当==时,

(10)

由式(10)可知,当cos=0时,det()取得最大值。因此双无人机观测目标的最优观测配置是无人机与目标之间的视线夹角为=π2,此时无人机能够获取更多有效的目标信息。

2.2 观测航迹优化控制

在双机协同跟踪目标最优观测配置分析的基础上,本节设计协同控制算法优化无人机的观测轨迹。假设无人机在固定高度飞行,因此可简化为无人机与目标水平方向的夹角保持在90°。针对超视距目标跟踪而言,无人机与目标相距较远,需要在趋近阶段优化无人机的观测轨迹,因此设计的协同控制算法在保证无人机趋近目标的同时,也要使得无人机与目标的视线夹角趋近90°,设计双机协同控制算法如下:

(11)

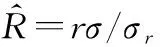
(12)

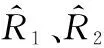
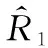
2.3 融合滤波

目标状态方程为

()=(-1)+()

(13)

式中：

()是均值为0、方差为的过程噪声;表示采样间隔。

观测方程为

(14)

式中：()是均值为0、方差为的观测噪声；、、分别表示无人机观测目标的距离、方位角和俯仰角。

CKF根据Cubature变换得到具有相同权值的容积点来近似积分运算,即

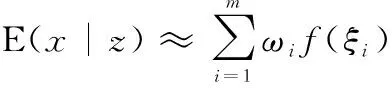
(15)

式中：

(16)

其中，[]表示维空间(维状态)的点集,[]表示集合的第列,对于三维目标跟踪,=6。

(17)

计算出容积点集后通过预测更新和量测更新便得到CKF滤波算法。

(1)融合状态估计:

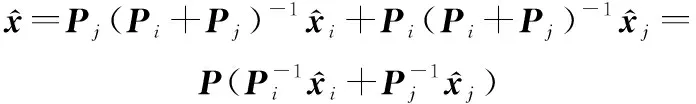
(18)

(2)误差协方差:

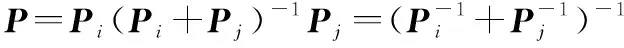
(19)

根据第1节和第2节的分析,双节协同跟踪算法结构如图2所示。协同控制模块根据当前时刻的无人机状态与目标估计状态,控制无人机在靠近目标的同时,使得无人机与目标之间的夹角接近90°。姿态校正算法模块通过无人机位置、无人机观测信息、辅助信标位置以及无人机原始的姿态角数据求解出校正后的无人机姿态角,从而减小姿态角误差。坐标变换模块将目标观测值变换到地理坐标系,得到减小姿态角误差后的目标观测值。随后将每个无人机观测到的目标状态送到信息融合中心,信息融合中心对目标进行融合滤波处理,消减观测随机误差对目标状态估计的影响。最后将得到的目标状态估计送入协同控制算法模块,控制无人机的飞行,形成闭合环路。

图2 双机协同跟踪算法结构图Fig.2 Structure diagram of cooperative tracking algorithm by two unmanned aerial vehicles

3 仿真结果

3.1 单机观测

设目标做匀速直线运动,目标初始位置位于(0 m,200 000 m,0 m)处,速度为8 m/s,方向角为π/4,过程噪声均值为0,协方差为0.01·diag([1,1,1]);辅助信标位于(0 m,0 m,0 m)处,无人机与辅助信标的距离为50 km,无人机高度为2 500 m;传感器观测目标的随机误差为(5 m,0.3°,0.3°);观测辅助信标的随机误差为(5 m,0.3°,0.3°),假设随机误差服从高斯分布;无人机姿态角固定误差为(0.1°,0.1°,0.1°),随机误差为(0.1°,0.1°,0.1°);仿真间隔1s,仿真时长1 000 s。

仿真200次,得到传统方法(包含姿态角误差)、姿态校正方法(本文方法)以及静态方法(无姿态角误差)情况下目标位置均方根误差(root mean square error, RMSE),如图3所示。

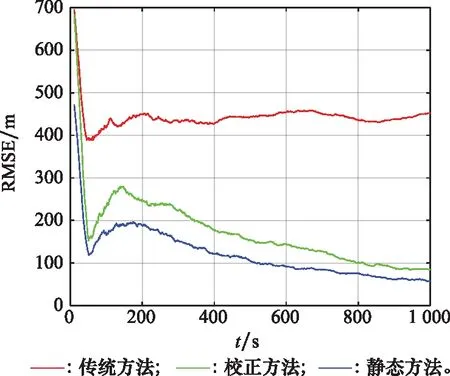
图3 单机观测时目标位置RMSEFig.3 RMSE of target position through observation by the single unmanned aerial vehicle

图3可以看出在终端时刻,单无人机采用传统方法观测得到的目标位置RMSE为451.8 m;采用基于辅助信标的姿态校正算法,目标的位置RMSE为83.7 m,相比较传统观测而言,定位精度得到了很大的提高;在没有姿态误差的理想情况下,目标位置RMSE为57.5 m。可见本文提出的姿态校正算法能够有效减小姿态角误差对定位精度的影响,提高目标定位精度。

同时，为比较不同滤波算法对目标位置精度的影响,图4给出了EKF、UKF、CKF三种滤波算法下的目标位置RMSE,蒙特卡罗仿真次数为200次。

图4 不同滤波算法下目标位置RMSEFig.4 RMSE of target position under different filter algorithms

图4的结果表明CKF算法具有较高的滤波精度,特别是在前200 s,CKF的滤波精度均明显高于EKF、UKF滤波算法,这十分有利于在尽可能短的时间内跟踪目标。

3.2 双机观测

采用单机观测的仿真参数,两架无人机距离辅助信标的距离均为50 km,相比较单机观测增加了无人机2的观测,观测态势如图5所示。

图5 双无人机对目标定位空间态势图Fig.5 Space situation diagram of target positioning by two unmanned aerial vehicles

同样仿真200次,得到双无人机观测条件下传统方法测量、姿态校正方法测量以及无姿态误差测量情况下目标状态估计误差,如图6所示。

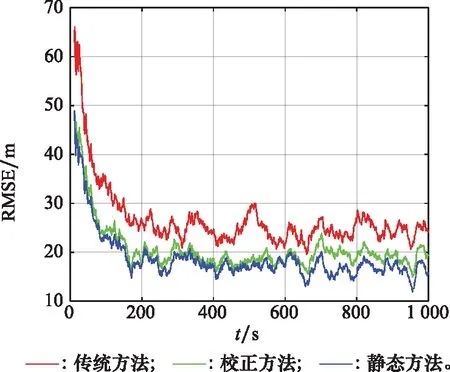
图6 双机观测时目标位置RMSEFig.6 RMSE of target position through observation by two unmanned aerial vehicles

双无人机观测时,采用传统方法观测得到终端时刻的目标位置RMSE为24.3 m;采用基于辅助信标的姿态校正算法,目标终端时刻的位置RMSE为19.4 m,在没有姿态误差的理想情况下,终端时刻目标位置RMSE为15.8 m。从仿真结果看出双机观测相比较单机观测能有效提高目标的定位精度。

3.3 双机协同控制观测

下面考虑双无人机协同的情况,无人机飞行速度为100 m/s,仿真运行1 300 s,采用式(11)的控制律得到无人机的运动轨迹如图7(a)和图7(b)所示,分别给出了在三维和二维空间中的双无人机运动轨迹;图7(c)给出了目标真实运动轨迹以及采用本文方法得到的目标估计运动轨迹。图8给出了无人机与目标之间距离、双无人机与目标之间夹角随时间变化曲线图。图9表示仿真200次,仿真时长为1 000 s时,无人机飞行过程中对目标观测定位误差的变化曲线。

图7 无人机与目标的运动轨迹Fig.7 Trajectory of unmanned aerial vehicle and target

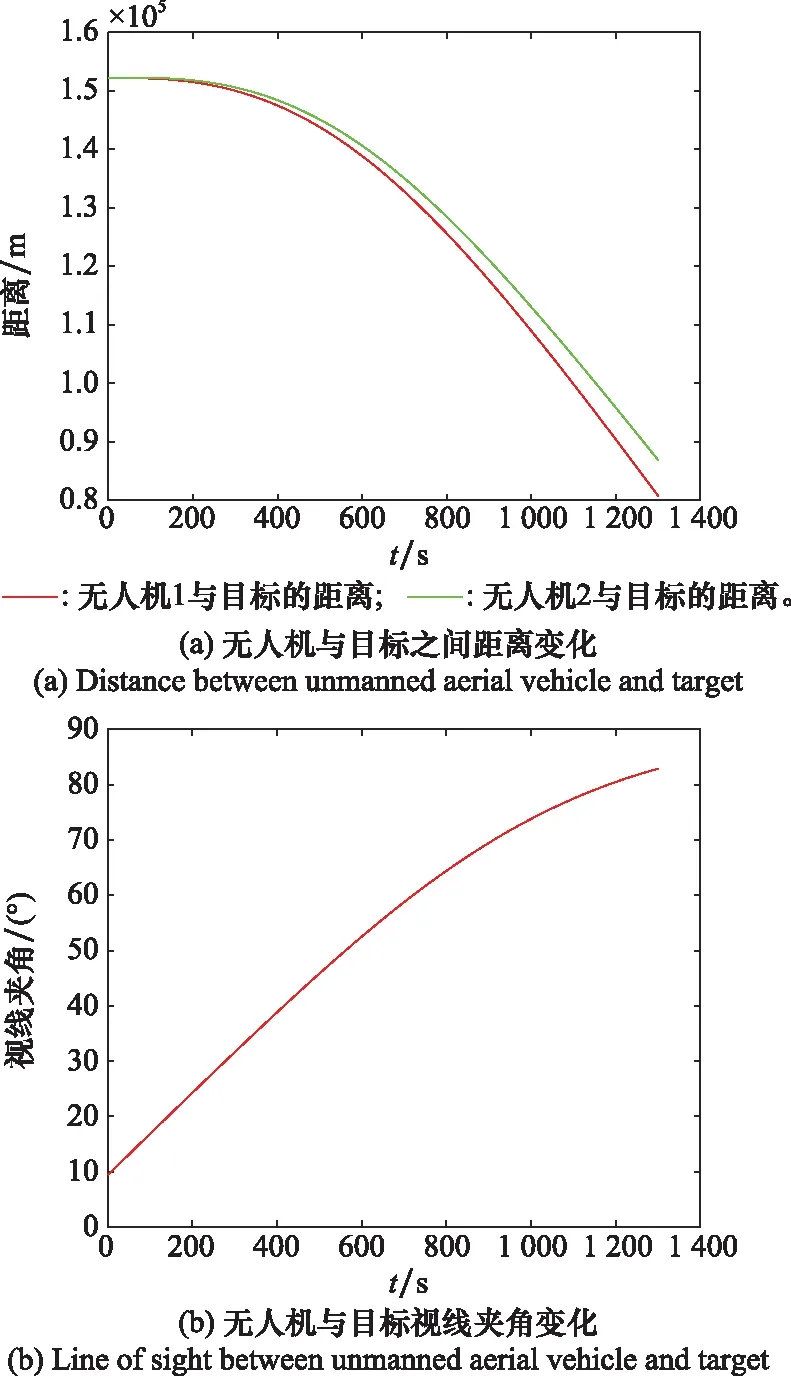
图8 无人机与目标之间距离和视线夹角变化曲线Fig.8 Distance and line of sight between unmanned aerial vehicle and target

结合图7和图8可以看出,采用式(11)的控制律,能够较好地控制无人机在靠近运动目标的同时,无人机与目标之间的夹角接近90°,使得无人机处于观测优化的位置。图9表明无人机观测的目标位置误差随着时间的变化而在不断的减小,相比较第32节双机观测而言,终端时刻目标位置的RMSE变小。仿真结果验证本文的算法能有效提高对目标的定位精度,从而达到对超视距目标精确定位的目的。

图9 双机协同观测时目标位置RMSEFig.9 RMSE of target position when two unmanned aerial vehicles cooperate to observe

为分析双机协同控制算法的有效性,与Lyapunov导航矢量场的方法进行了比较,Lyapunov导航矢量场为

(20)

通过导引矢量场得到无人机期望航向角:

(21)

应用反馈控制原理设计比例控制器:

(22)

(23)

两架无人机协同跟踪目标时,两架无人机的速度控制输入分别为

(24)

图10给出了Lyapunov导航矢量场规划的双无人机轨迹,图11给出了本文方法与Lyapunov导航矢量场法得到的目标位置RMSE对比图。从图11看出，本文提出的双机协同控制算法能取得较好的目标状态估计,而且估计性能优于Lyapunov导航矢量场法,验证了本文所提双机协同控制算法的有效性。

图10 Lyapunov导航矢量场规划的无人机轨迹Fig.10 Unmanned aerial vehicle trajectories planned by Lyapunov guidance vector fields method

图11 本文方法与Lyapunov导航矢量场法RMSEFig.11 RMSE of through the proposed method and Lyapunov guidance vector fields method

4 结 论

本文提出一种基于无人机对超视距目标的定位跟踪算法。提出基于辅助信标的姿态校正算法,通过无人机观测的辅助信标位置以及辅助信标已知的精确位置,减小无人机姿态角误差,从而消减无人机姿态角误差对定位精度的影响,并且得到了仿真验证。

多无人机相对目标的观测位置也会影响无人机对目标的定位精度,基于双机协同的最优观测构型与相对距离因子对最优轨迹的影响,设计一种双机协同制导律从而使得无人机处于观测优化的位置。仿真表明,所提控制方法能够控制无人机在靠近目标的同时,使得双机与目标之间的夹角接近90°,提高双无人机对目标的定位精度。

本文提出的算法能有效提高对超视距目标的定位精度,为超高速炮弹提供信息保障,具有一定的工程应用价值。