基于大地坐标系的IMM航空器短期航迹外推

2022-06-25汤新民郑鹏程

系统工程与电子技术 2022年7期

汤新民, 郑鹏程

(南京航空航天大学民航学院, 江苏南京 211106)

0 引言

随着空域内航空器密度的增加,管制员的负荷不断增加,当管制员负荷高于一定水平之后,空域内产生运行不安全事故的可能性会大大增加。对于在航路运行的航空器,飞行员的工作内容少、工作负荷低,因此,如果在航路飞行阶段将部分间隔保持责任由管制员移交给飞行员,可以在降低管制负荷的同时保证运行安全。

将间隔保持责任转移到飞行员的前提是该空域范围内的航空器具有感知周围环境态势的能力,在当前及可预见的未来一段时间内,航空器能够通过广播式自动相关监视(automatic dependent surveillance-broadcast, ADS-B)的接收功能(简称为ADS-B-IN)获取周围航空器的状态信息,但目前没有关于飞机广播意图信息的技术规范,所以难以获取周围航空器的意图信息,而周围航空器的意图信息使得本机能够预测他机在未来一段时间内的轨迹,若在计算间隔保证策略时能够获得他机的意图信息,将会极大地提升间隔保持策略的安全与效率。因此,需要根据航空器的历史状态信息推测航空器的意图信息,并根据航空器的意图信息进行外推,得到航空器在未来一段时间的外推航迹。

单运动模型跟踪算法在跟踪目标发生机动时会产生跟踪模型的失配问题,交互式多模型 (interacting multiple model, IMM)算法是在广义伪贝叶斯基础上提出的一种具有马尔可夫转移概率的算法,IMM算法考虑了目标可能处于的多种运动状态,分别建立多个运动子模型,并考虑子模型之间的交互作用,以达到对机动目标的自适应跟踪。

IMM算法的优劣取决于模型集的选取是否恰当,目前常用的模型集包括匀速运动模型、匀加速运动模型、协同转弯模型等,对机动目标加入Singer模型可以在目标发生机动时无需进行机动检测,就能进行无时间滞后的机动目标跟踪。Singer模型是一个零均值的一阶相关模型,该模型认为目标在加速度的均值为0,然而目标在机动过程中,下一时刻加速度的均值应该是当前时刻加速度的均值,因此,根据Singer模型进行改进得到的“当前”统计模型被广泛用于IMM算法运动模型集中。为了提高目标跟踪的精度,会尽量选取更多的模型加入到模型集中,从而使该算法能够覆盖尽可能多的运动情况,但是随着模型数量的增加,在每个时间段内的计算量会大量增加。此外,模型数量过多会导致模型间出现竞争问题,导致算法的性能下降。为了在保证跟踪准确率的情况下减小计算量,提出了一系列的变结构模型集的IMM算法,例如自适应网格算法、机动判别算法、有向图切换算法等。针对多普勒雷达目标跟踪中非线性的特点,以IMM算法为基本框架,根据最佳线性无偏估计的卡尔曼滤波和序贯滤波器更新模型概率,最后的估计是序列滤波器输出和模型概率的加权和,仿真结果表明该算法能实现较好的机动目标跟踪精度。针对复杂机动情况下跟踪精度低、易发散的问题,文献[21-22]对IMM算法中的滤波算法进行了改进,文献[21]提出了一种基于增益矩阵和转移概率矩阵实时动态调整思想的IMM强跟踪平方空间卡尔曼滤波;文献[22]提出了一种改进的IMM自适应强跟踪随机加权容积卡尔曼滤波;文献[23]提出了使用极限梯度提升(extreme gradient boosting, XGBoost)方法来替代最大似然估计方法计算目标最终的状态估计,从而最大化利用系统的先验信息。针对传统恒速度子模型和恒加速度子模型在降噪方面的不足,文献[24]改变了状态空间的结构,使用了动态状态转移矩阵,从而提高模型的收敛速度并降低噪声影响。

当目标的观测数据丢失,IMM算法采用的轨迹外推算法是将记录最后时刻各模型的概率取值,并根据模型的马尔可夫状态转移矩阵进行概率矩阵的外推,得到各个模型的概率取值后,各个模型交互得到该时刻目标的状态信息。

本文采用IMM算法,首先跟踪航空器的飞行航迹,并辨识航空器子模型的概率分布,然后预测航空器关键运动参数的变化趋势,最后根据末时航空器状态和子模型概率分布对航空器进行合理的短期航迹外推。

1 问题描述和目标运动模型

1.1 问题描述

机载ADS-B的发射功能(简称为ADS-B-OUT)可以将航空器的经度、纬度、高度、速度、航向、爬升率等信息编码后进行广播,本机的ADS-B-IN设备接收到ADS-B报文后进行解码,能够获取周围他机的状态信息,用于对周围空域内的他机进行追踪监视。对于机载自主间隔保持系统来说,周围航空器状态信息的准确性至关重要,因此本文采用IMM算法结合卡尔曼滤波对ADS-B报文中的航空器状态信息进行处理,辨识航空器的关键运动参数,最后根据航空器的运动趋势进行短期航迹的外推。

1.2 坐标系的选择

图1 空间直角坐标系中的航空器位置坐标Fig.1 Aircraft position coordinates in rectangular coordinate system

图2 空间直角坐标系中的线性外推航迹与理想外推航迹的对比Fig.2 Comparison between linear and ideal extrapolation track in rectangular coordinate system

图3 航空器在大地坐标系中的位置示意图Fig.3 Position of aircraft in geodetic coordinate system

1.3 目标运动模型

航空器的运动状态可以用如下的离散系统方程表示:

状态方程:

(+1)=()()+()()

(1)

观测方程:

()=()()+()

(2)

式中:()为状态转移矩阵;()为噪声驱动矩阵;()∈为状态方程白噪声,其协方差矩阵为();()为观测矩阵;()∈为观测噪声,其协方差矩阵为();()∈为系统在时刻的状态向量;()为时刻航空器状态的观测向量。其中,()与()为互不相关的零均值高斯白噪声。

在大地坐标系中,选取的目标航空器的运动状态变量为

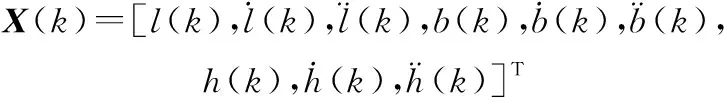
(3)

利用IMM算法跟踪目标航空器的关键在于选取适当的运动模型作为子模型,模型集应当能够覆盖航空器所有可能的运动状态。本文的模型集中共选取3个方向上的6个运动子模型,如表1所示。

首先对巡航阶段航空器运动状态进行分析,判断模型集能否满足覆盖性要求。

巡航阶段飞机可能的运动状态及模型集组合如表2所示。

表1 IMM算法模型集

表2 飞机可能的运动状态与子模型组合的关系

根据分析,可以看出表1中的模型集能够覆盖巡航阶段航空器的各种运行状态。

1.3.1 匀角速度-零速运动模型

(1) 经度方向,目标做匀角速度运动时,其连续时间状态方程为

(4)

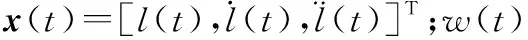
(+1)=()()+()()

(5)

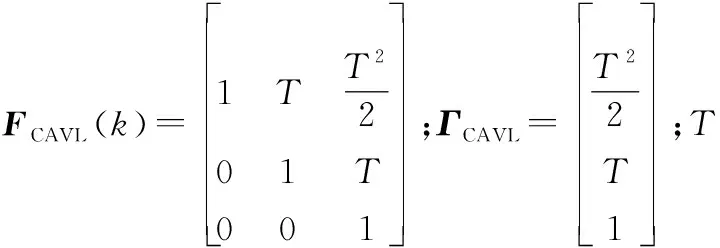
(2) 纬度方向,目标的匀角速度运动模型与经度方向的匀角速度运动模型一致,所以可得纬度方向的离散时间状态方程为

(+1)=()()+()()

(6)

其中,

=[2,, 1]

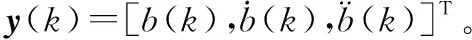
(3) 高度方向,由于零速运动模型中,航空器高度方向的速度为0,所以离散时间状态方程为

(+1)=()()+()()

(7)

其中,

132 “当前”运动模型

“当前”统计模型是对Singer模型的改进,Singer模型是零均值的时间相关模型,而实际上航空器下一时刻的加速度的均值是当前时刻的加速度,随机加速度在时间轴上仍然符合一阶时间相关过程,即

(8)

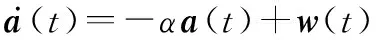
(9)

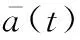
加速度的方差为

(10)

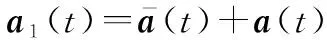
(11)

(12)

(1) 经度方向,目标做变加速运动时,根据式(11)与式(12)可得其连续时间状态方程为

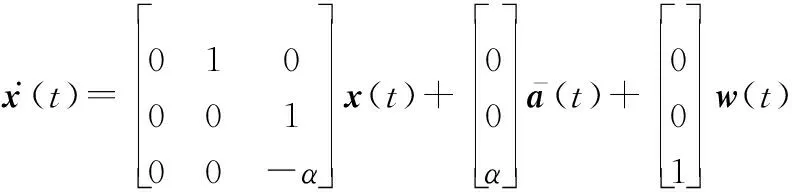
(13)

相应的离散形式的运动状态方程为

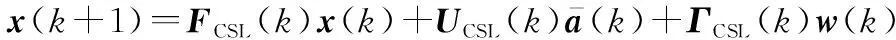
(14)

其中,

=[2,, 1]

(2) 纬度方向,目标的变加速运动模型与经度方向的变加速运动模型一致,所以可得纬度方向的离散时间状态方程为

(15)

其中,

=[2,, 1]

(3) 高度方向,目标做变加速升降运动时,根据式(11)与式(12)可得其连续时间状态方程为

(16)

相应的离散形式的运动状态方程为

(17)

其中,

=[2,, 1]

133 目标运动解耦

本文采用大地坐标系进行建模,在使用IMM算法跟踪目标航空器时,如果将经度、纬度和高度3个方向上运动模型结合在一起,可能会导致航空器在3个方向上的运动产生耦合现象。子模型的耦合作用会导致3个方向上的“匀角速度-零速运动模型”的概率取值相同,3个方向上的“当前”运动模型的概率取值也相同,这种耦合现象会导致跟踪效果较差,因此本文将3个方向上的运动进行解耦。

具体的解耦方法如下:

(1) 经度方向,对轨迹数据中的经度数据使用经度方向的“匀角速度运动模型”和“当前”运动模型进行跟踪;

(2) 纬度方向,对轨迹数据中的纬度数据使用纬度方向的“匀角速度运动模型”和“当前”运动模型进行跟踪;

(3) 高度方向,对轨迹数据中的高度数据使用高度方向的“零速运动模型”和“当前”运动模型进行跟踪。

将3个方向的跟踪数据进行合并,即可得到IMM算法的跟踪结果。

2 IMM算法

IMM算法是在广义伪贝叶斯基础上提出的一种具有马尔可夫转移概率的算法,其本质是将前一时刻多个模型的输出进行加权组合作为各个模型的当前输入,多个模型并行估计,最后得到组合状态估计。

完整的IMM 循环由以下4 部分组成: 输入交互、滤波、模型概率更新、输出交互。

假设IMM算法模型集包含有个模型,在时刻,从模型转移到模型(1≤,≤)服从一个给定状态转移概率的马尔可夫矩阵:

={()|(-1)}

(18)

2.1 输入交互

-1时刻,模型转移到模型的概率为

(-1)=·(-1)

(19)

因此,-1时刻,由其他模型转移到模型的总概率(归一化常数)为

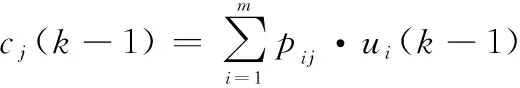
(20)

模型到模型混合概率为

(21)

模型的混合状态估计为

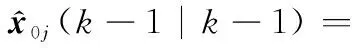
(22)

模型的混合协方差估计为

{(-1|-1)+

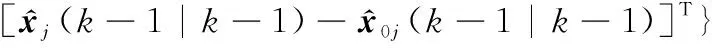
(23)

2.2 状态滤波

本文采用卡尔曼滤波算法作为各个子模型的滤波器对输入交互的结果进行滤波,首先根据状态转移方程计算模型的估计状态,然后将目标的观测数据作为先验信息来对状态估计进行修正,得到滤波后的状态估计。卡尔曼滤波的执行步骤如下。

根据状态转移方程进行状态一步预测:

(24)

一步预测的协方差矩阵为

(25)

卡尔曼滤波的增益矩阵为

()=(|-1)··[(|-1)+]

(26)

使用观测数据作为先验信息对目标状态进行更新:

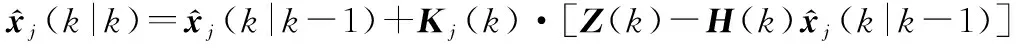
(27)

协方差矩阵更新:

(|)=[-()()](|-1)

(28)

2.3 模型概率更新

对于第个模型,其似然函数为

(29)

模型的概率更新方程为

(30)

2.4 输出交互

滤波器的总输出为对各个模型进行滤波后的估计结果的加权值,加权的状态估计为

(31)

加权后的协方差估计为

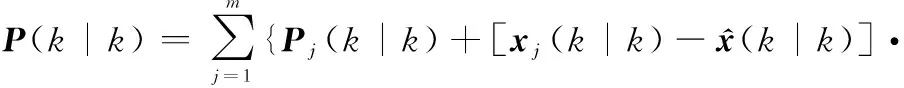
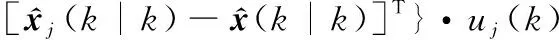
(32)

3 航空器航迹外推算法

IMM算法可以提供周围他机的当前状态信息,但是他机在未来一段时间内的航迹对于航空器自主间隔保持也是同等重要的,本节的主要内容是根据航空器的历史轨迹信息外推得到他机未来一段时间的航迹,为航空器自主间隔保持算法提供数据支持。

对于单一运动子模型的系统,可以根据最近一段时间的状态转移矩阵使用式(24)进行状态的一步预测,但对于含有多个子模型的系统,状态转移矩阵难以确定。

(33)

(34)

式中:()是时刻子模型的概率。由于子模型之间的转移概率服从马尔可夫过程,因此可以通过-1时刻各个子模型的概率(-1)和得出()：

(35)

4 仿真

4.1 航迹跟踪仿真

本文使用2021年3月3日,航班号为CCA1516的航空器的ADS-B轨迹数据进行滤波跟踪。首先,将采集过的数据进行可视化,判断轨迹数据是否连续,然后将采集到的ADS-B数据进行数据清洗,然后使用分段3次 Hermite 插值将离散的轨迹点插值成时间间隔=1 s的采样点,得到1 113个轨迹点。仿真采用的参数如下。

仿真得到的IMM跟踪轨迹和观测轨迹曲线图如图4所示。

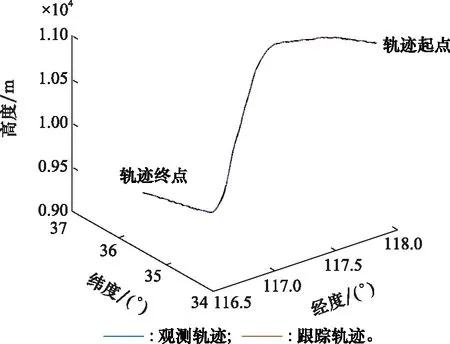
图4 航空器观测航迹和IMM跟踪轨迹曲线图Fig.4 Observation track and IMM tracking curve of aircraft

IMM算法跟踪误差曲线图如图5所示,可以看出,大部分时间段内,IMM算法跟踪的误差小于50 m,仅在极少数位置会出现大于250 m的误差,总体的跟踪效果较好。

图5 IMM轨迹跟踪误差曲线图Fig.5 IMM trajectory tracking error curve

IMM跟踪过程中,3个方向上,各个子模型的概率变化曲线图如图6所示。

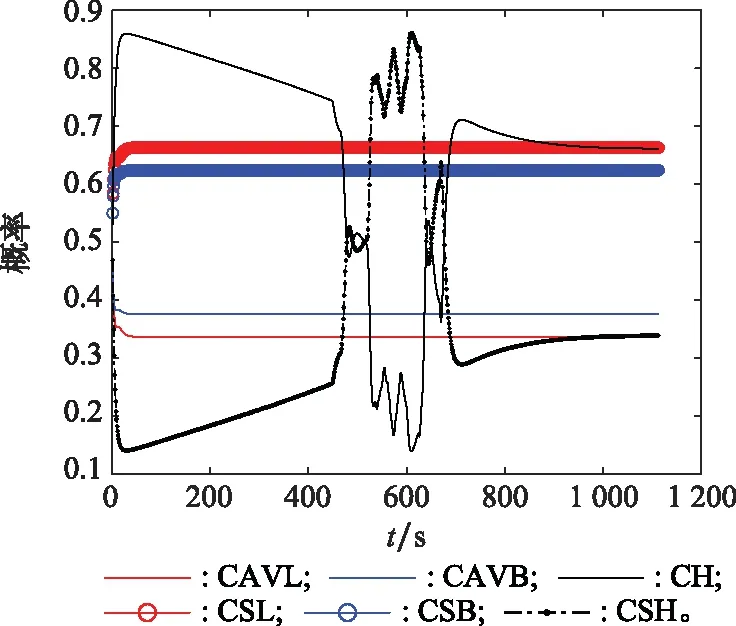
图6 子模型概率变化曲线图Fig.6 Probability variation curve of sub model

4.2 航迹外推仿真

选取某一时刻航空器的状态作为初始状态,外推时间为250 s,外推航迹与观测航迹的对比如图7(a)所示,外推航迹的误差随时间变化的关系如图7(b)所示。

图7 基于大地坐标系的航迹外推结果Fig.7 Track extrapolation result based on geodetic coordinate system

第1.2节仅从理论上说明了空间直角坐标系在航迹外推方面的不足,本节使用两种参考系,针对同一初始状态、使用相同的外推方法计算航空器的外推航迹。基于空间直角坐标系的外推航迹与观测航迹的对比如图8(a)所示,外推航迹的误差随时间变化的关系如图8(b)所示。

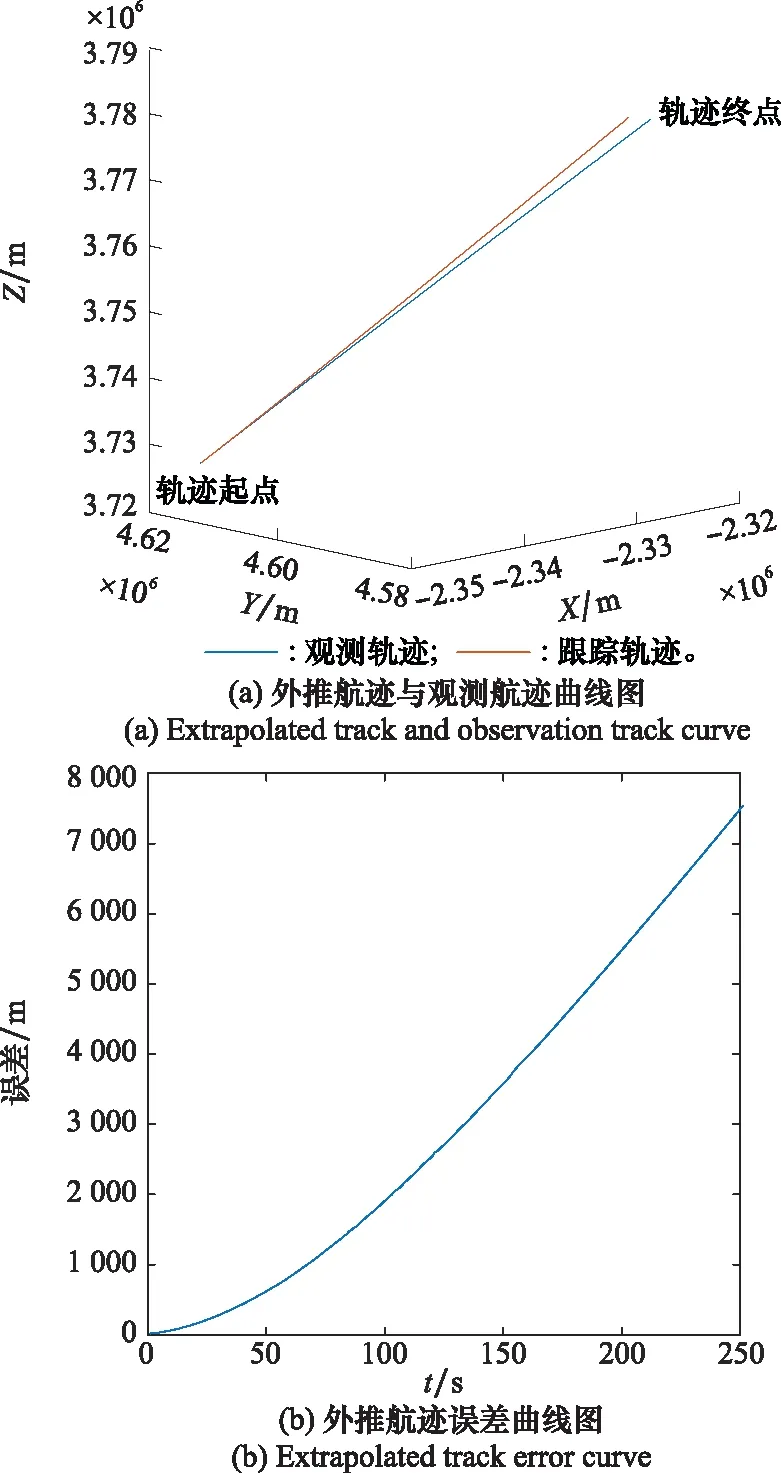
图8 基于空间直角坐标系的航迹外推结果Fig.8 Track extrapolation result based on spatial Cartesian coordinate system

基于大地坐标系和空间直角坐标系的航迹跟踪误差对比如图9所示,在航迹跟踪过程中,二者相对于观测航迹的误差均保持在较低的水平。

图9 大地坐标系和空间直角坐标系下的跟踪误差对比Fig.9 Tracking error comparison between geodetic coordinate system and spatial cartesian coordinate system

基于大地坐标系和空间直角坐标系的航迹外推的误差对比如图10所示。可以看出,随着外推时间的增加,基于空间直角坐标系的航迹外推的误差在70 s的时候已经增长到大约1 000 m,而此时基于大地坐标系的航迹外推的误差仅为50 m左右;在第250 s时,基于空间直角坐标系的航迹外推的误差超过了7 000 m,而基于大地坐标系的航迹外推的误差为700 m左右。仿真结果表明,基于大地坐标系在航迹外推方面比基于空间直角坐标系具有更好的性能。