基于置信椭圆的无人艇区域覆盖搜寻规划优化

杨少龙, 黄 金, 向先波, 李伟超

(华中科技大学船舶与海洋工程学院, 湖北 武汉 430074)

0 引 言

随着一带一路建设,海上经贸活动不断增加,随之海上事故频发。在发生海难事故时为了最大限度减少生命财产损失,海上应急救援需要准确、快速地估计搜寻区域,设计合适区域搜寻规划路径提高海上搜寻成功率(probability of success,POS)并减少搜寻时间,使搜寻力量(如无人艇)以最短时间完成对高概率区域覆盖式搜寻。

海上遇险目标搜寻区域确定是成功搜寻的重要前提。Breivik等人采用普林斯顿海洋模型分析海洋环境,建立了海上搜救模型,并利用蒙特卡罗模拟确定搜寻区域。肖方兵等人建立包含环境扰动的遇险目标漂移模型,通过蒙特卡罗随机粒子仿真法结合最优搜寻矩形规则确定搜寻区域。但蒙特卡罗随机粒子仿真法产生搜寻区域中少量边缘粒子远离中心高密度粒子区域,数量稀少且分布发散。随着时间推移,边缘粒子分布会更加分散,显著扩大待搜寻矩形区域面积。这对搜寻力量投入带来巨大负担,对于分秒必争的救援任务而言更需要对粒子高密度聚集区域以最短时间完成搜寻覆盖任务。

搜救力量是海上遇险目标搜寻规划执行主体,但有人搜寻力量难以胜任大面积、长时间、恶劣海况的区域搜寻任务。随着无人系统快速发展,无人艇、无人机等新生力量为海上遇险目标搜寻带来了新的机遇。以无人机为例, Bouzid等人、Martins等人研究无人机海上搜寻,但由于恶劣海况、恶劣天气、续航等因素难以长时间工作。相比之下,无人艇可在水面航行,对恶劣海况适应能力更强且续航满足大范围的区域搜寻。李亚南等人研究了无人艇集群对包含障碍的区域进行动态规划,较好地适应了动态环境,但具体到海上搜救应用场景,搜寻代价、区域覆盖程度等是更加重要的关注点。

区域覆盖搜寻问题在各领域广泛存在,受到国内外学者普遍关注。Choset等人首次利用boustrophedon细胞分解实现了机器人对区域的完全覆盖,但梳状规划路径未考虑机器人自身的操纵性限制。李亚南等人采用模仿独居动物社会行为的分布式反集群研究了无人艇集群区域全覆盖方法,同样忽略了欠驱动无人艇操纵性导致的转向路径跟踪问题。针对区域覆盖路径寻优,Li等人将航行距离与最大航行距离多目标优化问题转化为单目标优化。彭辉等人将多目标航路代价估计值和有效时间估计值加权求和转化为单目标优化。但这类多目标加权转化为单目标做法,在实际搜寻规划任务中却存在权值系数难以确定的问题。

为此,针对海上搜救区域搜寻规划面临的目标包含概率(probability of containment, POC)、搜寻探测概率(probability of detection, POD)表示搜救力量探测到搜寻目标的概率,以及搜寻代价等优化需求,开展基于无人艇的多目标优化搜寻规划方法研究,在最少搜寻路径代价下实现最大化搜寻POS=POC×POD,表示搜寻行动成功找到目标的概率。一方面,搜寻区域确定聚焦高密度区域及最佳POC;另一方面,搜寻规划优化实现总路径最短且POD最大。首先,建立海上遇险目标漂移粒子分布位置,然后依次对搜寻区域和搜寻路径进行优化求解。对于搜寻区域,设计一种基于腐蚀膨胀的置信椭圆搜寻区域确定算法,实现区域内粒子POC和单位面积粒子数达到全局最优。对于搜寻路径,为实现优化搜寻线间距、遍历次序等从而获取全局最优总路径和POD采用非支配排序的遗传算法(nondominated sorting genetic algorithm II, NSGA-II),该算法使用带精英策略快速非支配排序从而实现快速、准确的搜索性能。本文最后通过对比常规矩形区域的梳状路径搜寻规划,揭示所提方法在搜寻工作路径等指标的显著优势。

1 无人艇区域搜寻规划总体思路

无人艇区域搜寻规划总体思路如图1所示。搜寻任务分为两个阶段:一是根据已知海况信息以及船只失事前最后一次上传信息利用蒙特卡罗随机粒子仿真获得粒子初始位置分布,然后根据粒子分布特点采用聚类算法将粒子分类,最后采用规则区域确定算法锁定高密度区域,使得搜寻力量尽可能投入到高概率区域;二是根据搜寻区域位置和形状信息结合无人艇转向数学模型,进行多目标搜寻路径规划,同时满足最大化POD和最短总路径。

图1 水上遇险目标搜寻整体框架Fig.1 Framework of distress targets overboard searching

无人艇执行搜寻路径跟踪任务,通过艇载视觉、雷达、红外探测等传感器探测落水人员。单次任务结束后根据搜寻结果重复上述步骤,直至满足要求。

2 基于腐蚀膨胀的置信椭圆搜寻区域确定

2.1 海上遇险目标概率分布

海上遇险目标位置分布中包含多种不确定因素,导致目标漂移轨迹呈现多样性。为此,在文献[3]基础上采用蒙特卡罗随机粒子仿真法建立海上遇险人员漂移位置分布。预测时长0.5 h,风场、流场数据以及落水人员风压属性见文献。如图2所示,海上遇险目标概率分布呈现较为明显的类簇特征,且边缘粒子分布相对分散。

图2 海上遇险目标概率分布Fig.2 Probability distribution of targets in distress at sea

2.2 海上遇险目标概率分布聚类

如图2所示,若直接利用矩形区域框选包括所有粒子来确定搜寻区域,则会显著增大搜寻代价,且在粒子低密度区域浪费搜寻力量。因此,采用聚类算法将所有粒子分簇,再结合分簇结果设计合理的搜寻区域。传统K均值聚类算法是不考虑概率特性的计算点与类簇中心的欧式距离来判定归属,不适应本场景应用,因此采用高斯混合模型(Gaussian mixture model,GMM)进行聚类,假设GMM模型由组高斯模型组成,对应GMM概率密度函数如下:

(1)

其中,第组分模型概率密度公式为

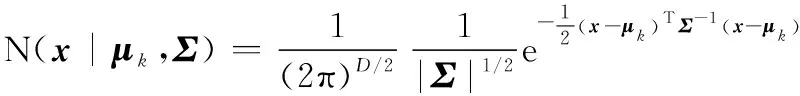
(2)

式中:为权值;为均值;为方差;为数据维度(=2);为高斯模型数;为描述二维坐标的样本向量。

首先确定模型组数值,结合图2分布特征设定=2,然后使用最大期望算法迭代求解直至产生的新聚类中心与上一次聚类中心差值小于预设常数0005,结束后将获得所有粒子分簇的划分结果。如图3所示,粒子分布呈现两个类簇。此外,少量粒子显著远离类簇中心且呈相对分散的特征,从搜寻角度而言需要投入相当大的搜寻代价才能完全覆盖这些概率密度较低的分散区域,不利于提高搜寻效率。

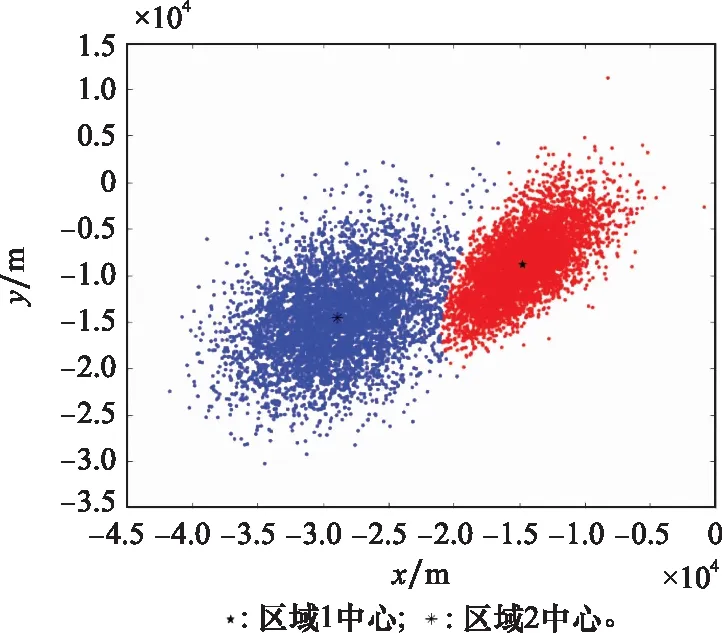
图3 基于GMM聚类粒子分布图Fig.3 Distribution of GMM-based clustering particles

为此,进一步设计基于腐蚀膨胀的椭圆搜寻区域确定算法,聚焦高密度区域提高搜寻效率。

2.3 基于腐蚀膨胀的椭圆搜寻区域确定算法

基于腐蚀膨胀的置信椭圆搜寻区域确定算法分为3个步骤。

根据聚类结果分别求出各类数据均值以及数据协方差矩阵对应的特征值和特征向量。

获取最大特征值并求出对应的特征向量,求出最大特征向量与轴夹角。

根据椭圆公式构造卡方检验,其中自由度为2,选取置信度为95%,可得椭圆长短半轴公式为

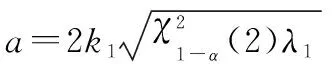
(3)

(4)

式中:,分别为椭圆长半轴和短半轴;为置信度;,分别为协方差矩阵的最大和最小特征值;,为腐蚀膨胀系数。

通过上述3步获得置信椭圆中心、长轴和短轴,从而确定椭圆面积和边界。通过调节腐蚀膨胀系数可以改变区域大小从而改变单位面积粒子数和POC。为了获取全局最优单位面积粒子数和POC建立了如下多目标优化模型:

max POC

(5)

(6)

式(5)与式(6)分别表示优化目标POC(椭圆内粒子数除以随机粒子总数)和单位面积的粒子数,其中表示产生随机粒子总数。

采用基于非支配排序并结合拥挤度算子求解该多目标优化问题,确定最佳腐蚀膨胀系数。根据椭圆区域特点,腐蚀膨胀系数范围为08～12,步长001。以图3中红色粒子区域1为例,对不同腐蚀膨胀系数下POC和单位面积粒子数进行非支配排序并结合拥挤度算子得到优化结果如图4所示。

图4 不同腐蚀系数下POC和单位面积粒子数Fig.4 POC and number of particles per unit area under different corrosion coefficients

基于最优前沿面采用拥挤度算子对结果排序得到拥挤度最小值所对应的腐蚀膨胀系数即全局最优腐蚀膨胀系数,即图4中点取值。选择图4中最优前沿面上、、点绘制椭圆区域,如图5对比可见,红色椭圆区域相比于蓝色区域单位面积粒子密度更高,可缩小待搜寻区域;与青色区域相比,红色椭圆区域POC概率更高。

图5 不同腐蚀膨胀系数下椭圆区域Fig.5 Elliptical region under different corrosion expansion coefficients

基于此方法优化得出两组聚类粒子的最佳置信椭圆区域如图6所示。区域1长轴腐蚀膨胀系数=093,短轴腐蚀膨胀系数=099,POC概率为0469。区域2长轴腐蚀膨胀系数=092,短轴腐蚀膨胀系数=101,对应POC为0473。两个区域整体POC概率为0942。

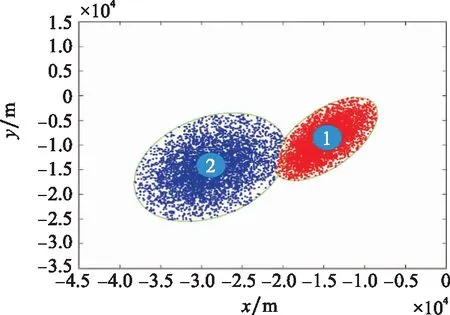
图6 基于腐蚀膨胀的置信椭圆区域Fig.6 Confidence ellipsoid region based on corrosion expansion

3 无人艇区域覆盖搜寻路径规划

3.1 问题描述

通过第2节确定最佳搜寻区域后,欠驱动无人艇需要设计合适的搜寻规划路径完成区域覆盖任务。采用NSGA-II算法同时考虑搜寻总路径与POD双目标优化问题,结合非支配排序和拥挤度算子求得非支配解更接近真实Pareto最优解集,适用于本场景问题。

3.2 问题建模

欠驱动无人艇搜寻区域路径规划主要关注搜寻总路径和POD两个目标。其中,搜寻总路径包含工作路径和非工作路径,工作路径为无人艇在搜寻区域内所有直线作业行路径总和,非工作路径为各作业行转向路径总和。执行任务过程中需要满足约束条件包括:① 转向路径最短;② 转向次数最少;③ 每条作业行均被遍历一次且不回起始行。约束条件中转向路径需依据无人艇操纵特性建立转向数学模型,根据欠驱动无人艇转向特性和作业行间距建立了U型和Ω型两种转向类型。如图7所示,其中P1B1、P2B2为工作路径,B1B2之间圆弧段路径为非工作路径,为当前作业行与下一条作业行之间的间距,两个圆心距表示无人艇最小回转直径,=arccos()。

图7 两种类型转向模式Fig.7 Two types of steering modes

受椭圆搜寻区域边界特征影响,搜寻区域内各条直线作业行长度不一(如和点),这会对无人艇的转向路径决策带来影响。为此,建立适应不同高度差的无人艇转向数学模型为

=|·tan-Δ|+

(7)

(8)

式中:、表示作业行路径编号≠;表示从当前作业行驶出到驶入下一条作业行的转向路径总长度;=(π2+);Δ=|-|表示第作业行和第作业行高度差,其中式(7)和式(8)分别对应于图7中Ω型转弯模式和U型转弯模式。

将作业行总路径和POD作为优化目标,以起始作业行、作业行遍历顺序和搜寻线间距为变量,以椭圆长轴方向为搜寻方向,可建立描述该问题数学模型。其中作业总行数计算式为

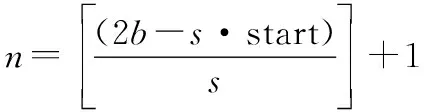
(9)

式中:为相邻两条搜寻作业行间距,即搜寻线间距;start为搜寻作业起始行,总行数计算为向下取整;为决策变量,表示是否包含从行到行的转向路径,其中=0表示不包含,=1表示包含;为无人艇扫海宽度;表示集合{1,2,…,};||表示集合中元素个数,则整体优化模型表述如下:

(10)

s.t.

=, ∀,∈

(11)

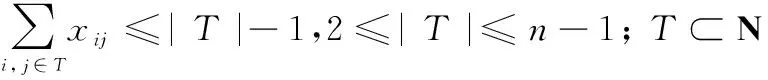
(12)

∈{1,0},,∈;≠

(13)

式(10)为优化目标函数,要求总路径最短且POD最大;式(11)表示转向路径具有对称性即从行到行与从行到行转向路径长度相等;式(12)与式(13)表示每条作业行有且仅被遍历一次且最终不回到起始行。

3.3 NSGA-II优化算法设计

利用NSGA-II算法获得最优起始行、作业行遍历顺序和搜寻线间距,实现总距离和POD值最优,整个过程分为以下3步。

设定群体规模、编码长度、交叉概率、变异概率以及最大遗传代数等参数,根据无人艇航行性能确定搜寻线间距范围和间距步长。

利用遗传算法产生初始起始行和作业行遍历顺序初始值,然后按照确定搜寻线间距计算在起始行确定条件下,遗传算法确定最佳遍历顺序,由此确定每个子代总路径和POD,采用非支配排序和拥挤度算子获取父代和子代合并后新子代作为下一次计算的父代,反复迭代直至达到终止条件并保存最优总路径和POD。

依据搜寻线间距步长改变搜寻线间距重复步骤2直至达到搜寻线间距范围上限。然后利用非支配排序并结合拥挤度算子获得不同搜寻线间距下拥挤度最小值即全局最优总路径和POD,最后输出最优值所对应的起始行、作业行遍历次序和搜寻线间距,上述步骤伪代码如算法1所示。

算法 1 无人艇路径优化算法01 输入:N,Gen,Gen1,Pc,Pm,S;∥输入种群大小N,起始行最大遗传代数Gen,遍历顺序最大遗传代数Gen1,交叉概率Pc,变异概率Pm,搜寻线间距范围S02 输出:s[];∥输出Pareto非劣解集03 for i=S_min:S_step:S_max04 Chrom=crtbp(N,PRECI);∥得到初始种群05 for j=1:Gen06 MP=Mating(Chrom,FrontValue,CrowdD istance);∥二元锦标赛选择07 SelCh=recombin(‘xovsp’,Pc);∥单点交叉08 Chrom=mut(SelCh,Pm);∥变异09 Sobj=object_calculation(Chrom);∥获取每个种群初始行10 for m=1:Gen111 Tobj=TSP(Sobj, PRECI);∥获取每个种群最优遍历顺序所对应总路径和POD12 end for13 FrontV=NonDominateSort(TObj);∥快速非支配排序

14 CrowdD=CrowdDistances(TObj,Fron tV);∥拥挤度距离计算15 end for16 [distance POD]=find_sort(FrontV,CrowdD);∥该搜寻线间距下最优值17 save=[save; distance POD];∥保存最优值18 end for19 best_FrontV=NonDominateSort(save_best);20 best_CrowdD=CrowdDistances(save,best_FrontV);21 [d P]=find_sort(best_FrontV, best_CrowdD);∥获得不同搜寻线间距下最优值

4 算法应用实例

算法求解在Matlab 2017b中实现,仿真计算机为Intel(R) Core(TM)i5-6200U CPU @ 2.30 GHz、内存12 GB、操作系统Windows10 64位系统。将世代距离(generational distance,GD)引入作为整体收敛性评价指标,GD值越小表明越接近真实Pareto最优解集。此外,海上搜寻规划通常以矩形区域框选感兴趣范围,且基于最小跨度理论规划平行线扫描方向减少无人艇往复转弯次数。因此,本文以椭圆最小外接矩形作为对比,长轴为长边,短轴为短边,且短轴是最小跨度方向,根据该外接矩形搜寻区域进行搜寻规划性能比较。

NSGA-II算法中初始参数设定为:种群大小为100,最大遗传代数为Gen为200,交叉概率Pc为0.9,变异概率Pm为0.05,搜寻线间距范围为0.1～0.2 nmile,扫海宽度为0.2 nmile,区域1的椭圆长半轴为5.21 nmile,短半轴为2.36 nmile,区域2的椭圆长半轴为6.31 nmile,短半轴为4.56 nmile,无人艇最小回转直径为8 m。

以图6所示椭圆区域1为例,区域覆盖路径规划结果表明当搜寻线间距步长0.02 nmile时,在搜寻线间距为0.12 nmile时,总路径和POD值达到最优,分别为337.04 nmile和0.811,作业行遍历顺序为按序依次遍历,Pareto前沿面如图8所示。

图8 区域1优化结果的Pareto前沿面及规划路径Fig.8 Pareto front of area 1 optimization result and planned path

NSGA-II算法优化结果GD值为0.015,接近于0,表明所求得解接近真实Pareto最优解集。基于Pareto最优前沿面解采用拥挤度算子对结果排序从而获得拥挤度最小值即全局最优解,根据所得最优解对应的作业起始行、作业遍历顺序和搜寻线间距可得到搜寻规划路径。如图8左上角区域1所示规划结果,图8右下角为路径局部放大图,可见无人艇转向过程以U型连接两条作业行,符合无人艇转向特性,且具有较短的非工作路径。

为了对比常规矩形区域和椭圆区域在搜寻工作路径和POD等方面的指标差异,以椭圆区域1的外接矩形区域进行搜寻规划,通过优化作业起始行、作业行遍历顺序和搜寻线间距获得全局最优总路径和POD,对比结果如表1所示。椭圆区域POD比矩形区域略大,但由于POC小于矩形区域,导致两者POS相等。本场景下搜寻线间距远大于无人艇最小回转直径,因此,两种搜寻区域均采用U型按序依次遍历完成路径规划。然而,对比总路径,椭圆区域比矩形区域少23.4%,可以有效减少搜寻路径代价。

表1 椭圆区域1和矩形区域1的搜寻指标对比

按照同样方式对椭圆区域2进行计算,结果表明当搜寻线间距为0.12 nmile时,总路径和POD值最优且最优值分别为719.98 nmile和0.811,所规划路径顺序为按序依次遍历。优化结果所对应的Pareto前沿面如图9所示,GD值为0.032。区域1和区域2总体POS为0.764,对应总路径为1 050.42 nmile。

图9 区域2优化结果的Pareto前沿面及规划路径Fig.9 Pareto front of region 2 optimization result and planned path

对比两个椭圆区域的外接矩形区域所规划结果可知,矩形区域总体POS为0.769,总路径为1 384.13 nmile。由此,相比常规矩形区域搜寻规划方法,本文所提椭圆区域搜寻路径规划方法在POS几乎不变的情况下,缩短搜寻路径代价达0.318,为实际海上应急搜寻提供了高效的搜寻决策依据。

5 结 论

本文提出面向遇险目标单向搜寻的无人艇区域搜寻规划方法。首先利用GMM聚类算法对蒙特卡罗随机粒子仿真法产生初始粒子聚类,然后采用基于腐蚀膨胀的置信椭圆法确定被搜寻区域,最后采用NSGA-II多目标优化算法对搜寻区域进行合理规划。

主要贡献和创新点有:① 采用GMM聚类算法对粒子分类,将粒子分类成多个区域,减少后续搜寻区域确定中不必要的搜寻面积;② 通过基于腐蚀膨胀的置信椭圆法确定全局下最优搜寻区域,使得区域内POD和单位面积粒子数全局最优,保证搜寻聚焦高密度区域;③ 建立面向椭圆区域边界特征的欠驱动无人艇转向模型,减少非工作路径长度,提高搜寻效率;④ 采用NSGA-II多目标优化算法对总路径和POD进行优化获得全局最优起始作业行、搜寻线间距和搜寻作业行遍历次序,达到满足一定搜寻成功率前提下,缩短搜寻路径代价达31.8%,提高搜寻时效性。