顺势而为：认知从“结论”走向“结构”

丁洪

[摘 要]剖析“从条件出发分析的策略”的流程、要点和表征，提出“顺势而为”的学习三部曲，做到在调用旧知中激活认知“感觉”、在解决问题中凸显认知“方法”和在迁移运用中内化认知“结构”，驱动学生从“认知舒适区”顺势走向“认知拉伸区”，实现策略学习从“点状性结论”转为“结构性认知”。

[关键词]顺势而为;从条件出发的策略;结构性认知

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）11-0007-03

“从条件出发分析和解决实际问题”是苏教版教材三年级上册安排的“策略学习”的专题活动，是学生策略学习的起始课。从信息加工的流程看，它沿袭“从已知条件出发，有序地推向未知”的操作路径，渗透合情推理的基本思想;从信息加工的要点看，它需要对条件进行合理选择、即时判断和有机整合，凸显信息关联的必要性。从信息加工的表征看，它强调过程经历的个性体验与共性建构，内化策略模型的认知。策略学习的主体是学生，教学需要尊重学生、依靠学生和发展学生，驱动他们从“认知舒适区”顺势走向“认知拉伸区”，最终实现策略学习从“点状性结论”转为“结构性认知”。

一、顺势调用旧知，激活认知“感觉”

策略学习的前期铺垫比较特别，一般表现为分散性、经常性和示范性地渗透，学生也许不清楚策略的具体名称，但是有关策略的真实体验和价值判断从未间断，激活这些原始的策略感觉，有助于思维活动的无缝对接。

1.选择条件，感觉有关联

首先，出示“小猴摘桃”的主题图，师生简单互动之后，借用“小猴帮妈妈摘桃，第一天摘了30个。第二天摘了多少个？”的问题，驱动学生读懂数学信息后尝试建立条件和问题之间的联系，从而发现缺少中间条件的客观事实。然后，提供两个条件，即“第二天比第一天多摘5个”和“第三天比第二天多摘5个”。学生自主选择条件之后，在“为什么都选第一个条件而不选第二个条件呢？”的追问中产生思维冲突和明辨是非的需求，发现尽管第二个条件也建构了“第二天和第三天之间的直接联系”，但是第二个条件与第一个条件不匹配、无联系，如果选择第二个条件反而增加了问题个数，人为制造了麻烦。经历了这样的综合判断之后，学生逐渐达成“只有条件之间有联系，条件与问题之间有联系，才能顺利解决问题”的共识。最后，再次聚焦“第一天摘了30个”和“第二天比第一天多摘5个”这两个条件，通过“哪个条件更值得我们多看几眼和细细品味？”的问题，驱动学生感知条件的复杂程度和锁定问题的思考重心。至此，条件和问题之间的正向关联悄然激活。

2.梳理经验，感觉有规律

首先，出示“上午摘了120个，卖出60个。下午又摘了80个，现在有西瓜多少个？”的问题情境，引导学生读一读文字、理一理内在关系、说一说如何解决。学生口头列算式“120-60+80=140（个）或120+80-60=140（个）”后感知“算法虽然不一样，但均是从条件出发”。接着，出示“运来4车水泥，每车150袋。用去320袋，还剩多少袋？”的问题情境。学生的学习经历与上一个问题差不多，不同的是，这里只能先求运来水泥的总袋数，然后减去用去的袋数，得到“还剩”的袋数，学生对比后感知“算法虽然单一，但均是从条件出发”的方向不变。最后，同时呈现两个问题的解题思维过程和逻辑结构条件（如图1），学生对比后感知“情境虽然不一样，但均是从条件出发”的方向相同。至此，从条件到问题的策略方向变得一目了然。

显然，策略教学可以借助“不良问题结构”，或者是原有“典型的问题梳理”，通过有层次、有对比和有沉淀的思维活动，帮助学生顺利调用和充分激活原有认知。

二、顺势解决问题，凸显认知“方法”

为了使“从条件出发分析和解决实际问题”的学习感觉更充分、更专注和更自然，需要设计相对复杂、适切和充满童趣的问题情境，以引导学生理解关键条件、尝试个性解决和积极对比，进而凸显认知方法的结构化、多样化和共性化。

1.理解条件，方法有勾连

首先，出示完整的例题“小猴帮妈妈摘桃，第一天摘了30个。以后每天都比前一天多摘5个。第三天摘了多少个？第五天摘了多少个？”。学生读题后，在“题中有哪些已知条件？要求什么问题？”的问题驱动下将数学信息进行合理分类，并锁定解决问题的关键，即“每天都比前一天多摘5个”。然后，鼓励学生运用自己喜欢的方法，讲清楚关键条件的内涵，得到“第二天比第一天多摘5个，第三天比第二天多摘5個，第四天比第三天多摘5个……”和“第一天摘的个数加5等于第二天摘的个数，第二天摘的个数加5等于第三天摘的个数，第三天摘的个数加5等于第四天摘的个数……”，并形成相应的思维结构。最后，引导学生观察和对比，发现“每天都比前一天多摘5个”包含许多结构相同的信息，整体描述比较简洁，点状描述比较具体，两类描述各有优势，可以根据需要灵活选择。这样处理，两种描述的切换将会变得更自然。

2.尝试解决，方法有个性

关键条件理解清楚了，就可创设自主探究活动，提出“先在学习单上试一试，再在小组内说一说”的要求，放手让学生以小组为单位进行尝试解决。基于原有认知的基础、习惯和风格，学生的表现不尽相同：有的直接数数，如“30、35、40、45、50”，一天接着一天数，依次数出了结果;有的画表格，对应填写每天摘桃的情况，依次列举出了结果;有的列式计算，从第二天开始，将每天摘桃的情况用简单的算式记录下来，如“30+5=35（个），35+5=40（个），40+5=45（个），45+5=50（个）”，依次算出了结果……令人惊喜的是，有学生运用每天桃子数量之间的相差规律，直接写出了结果“30+5×2=40（个）”和“30+5×4=50（个）”。在集体展示环节，学生走上讲台，展示组内探究成果，介绍具有个性的解题方法，说出具体的解题过程，学会质疑、补充和说明。这样处理，一方面可以引发榜样示范效应，为学生互助互学提供条件;另一方面可以引导学生自信表达，为学生持续学习注入活力。

3.对比过程，方法有共性

问题成功解决为策略提炼奠定了现实基础。通过呈现列表和列式的解决问题过程（如图2），结合问题“回顾解决问题的过程，你有什么体会？”驱动学生观察、对比和抽象，获得“要弄清题中每个条件的含义，看清要求的问题”“可以从条件开始出发，确定先算什么，再算什么”和“可以列式计算，也可以列表找出答案”的体验，得出“像这种读题目、理关系和顺着推来解决问题的方法，就是从条件出发分析和解决实际问题的策略”的结论。这样处理，明确了“不同方法中存在相同策略”在本课策略学习中的主体地位。

显然，策略教学需要 “全方位展示”和“全过程渗透”具体方法。也就是说，只有注重具体方法的细化凸显和前后关联，学生才有可能超越问题情境和解决问题方式，实现从具体方法到相关策略的认知进阶。

三、顺势迁移运用，内化认知“结构”

检测学习效果的最佳方式就是即时运用。一是运用所学策略“举一反三”，指向不同情境中的个性结论;二是提炼所用策略“举三反一”，指向不同情境中的共性结构。只有迁移运用和返璞归真辩证统一，才能内化认知“结构”。

1.迁移展示，结构有特点

首先，选择的是与“食”有关的问题情境。呈现两个保持平衡的天平，第一个天平的左边放4个桃子，右边放400克砝码;第二个天平的左边放1个橙子，右边放1个桃子和20克砝码。问：橙子多少克？学生根据“（   ）和（ ）可以求出（  ）”的思维支架，迅速进入观察对比、提取信息和解決问题的状态。在个人努力和小组合作交流后，学生的汇报有条不紊：从第一个天平中可以看出“4个桃子的质量=400克砝码”，所以1个桃子的质量就是100克;从第二个天平中可以看出“1个橙子的质量=1个桃子的质量+20克砝码”，结合刚才已知的桃子质量，可以很快地求出1个橙子的质量是100+20=120（克）。显然，学生已经能够独立地从条件出发，依次分析数量关系、联结两个条件和顺势解决问题。不过，这里的问题情境相对简单，有策略迁移的过程，但是策略水平相对较低。

其次，选择的是与“衣”有关的问题情境。先呈现一组杂乱信息，分别是“每天能加工80件上衣”“第一批加工了60条裤子”“一共生产了260双手套”“已经加工了3天上衣”“后来又加工了20件上衣”“第二批加工了200条裤子”和“猴子们领走了120条裤子”。学生利用空白的思维流程图，通过选条件、编题目、填信息、说过程等活动，完整经历策略的生长过程。显然，这里的问题情境相对复杂，学生既需要先行判断条件之间的关联程度，将杂乱的信息合理分类，又需要将同一类信息按照内在逻辑填空。这两项操作使得学生的策略水平得到有效提升。

再次，选择的是与“行”有关的问题情境。呈现“猴子们推着车往仓库运桃子。猴妈妈数了数，发现18辆车排成一排。从前往后数，它的女儿欢欢推着第8辆车;从后往前数，它的儿子乐乐推着第4辆车。欢欢和乐乐之间有几辆车？”这一问题情境。活动单上用“○”表示小车，引导学生扣条件、描位置和数结果。这里虽然没有复杂的数量关系，但是从条件一步一步地“推向”问题，主题不但没有变，反而在某种程度上被强化了。

最后，选择的是与“住”有关的问题情境。呈现“猴王决定让第一个正方形仓库里‘住’2筐桃。之后每个仓库‘住’的筐数都是前一个仓库里的2倍。每个装桃的筐都同样大。估计从第几个仓库开始，桃就不能继续按这样的规则‘住’进仓库了？”这一问题情境，引导学生在活动单上用大方格表示仓库，在第一个方格里用两个“○”表示已经“住”的筐数。学生锁定关键条件，依次画出示意图，然后顺势解决问题。可以看出，这里除了有数量多少的理解，还有空间大小的判断，更关键的是从条件出发的策略意蕴浓郁。

显然，借用“衣、食、住、行”的生活情境统整练习进行策略教学，有助于零散性问题和碎片化情境的融合，切实为学生提供了难度适中和喜闻乐见的学习环境和思维场域。

2.对比提炼，结构有模型

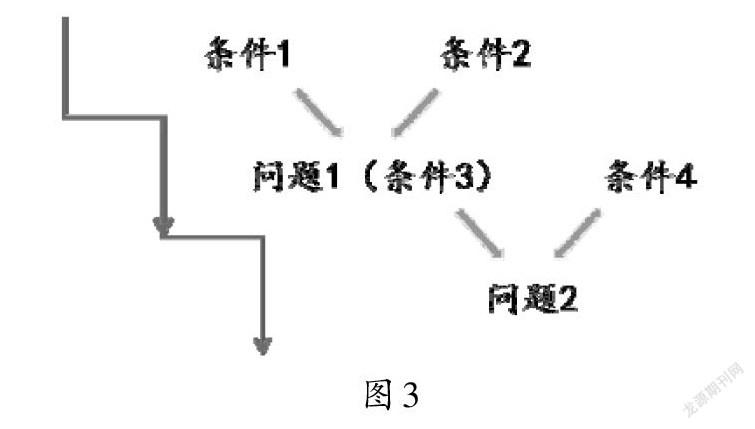
首先，对比感知策略的起点。要求欢欢和乐乐之间有几辆车，需要顺着条件定好位置;要求橙子多少克，需要确认和运用中间条件（问题）;要求“衣”中的问题，需要在众多条件中进行选择、分类和重组;要求“估计从第几个仓库开始，桃就不能继续按这样的规则‘住’进仓库了？”这一问题，需要有序解构整体描述的关键条件，凸显“分析条件”的策略起点。其次，对比感知策略的方向。情境不一样，算法有差别，但是从条件出发之后，始终瞄准问题，凸显“执因索果”的策略方向。最后，对比感知策略的结构。每个问题情境都有结构，换句话说，两个相关的条件可以解决一个问题，再把这个问题当成“中间条件”，与另一个相关条件结合，又可以解决下一个问题，以此类推（如图3），凸显“分级推理”的策略结构。显然，学生已经从“一步一景”的感性认知逐渐走向了“美美与共”的理性建构。

3.适度拓展，结构有智趣

有些故事不但蕴含丰富的数学知识，而且折射一定的数学道理，充分挖掘、筛选和凸显其中的教育元素，能够启迪智慧，激发兴趣。因此，利用“棋盘上的麦粒”的经典故事，能够使得学生：一是感受麦粒摆放的规律——每格摆放麦粒的数量是前一格的2倍;二是感知统计麦粒总数的困难，棋盘有64格，每格按规律摆放麦粒，虽然策略的起点、方向和结构都是对的，但是受思维的局限，近处可感，远处未知;三是感悟“棋盘上的麦粒”故事透射出的态度，有国王的傲慢，有大臣的睿智，还有慎重许诺的哲理，等等。换个角度来说，策略学习与策略运用是认知修炼的有机组成部分，前者是从案例抽象出策略，后者是运用策略解决了案例问题，两者均是螺旋上升和循环往复的。

纵观课堂，教师基本做到了“顺势而为地教”，实践了“眼中有策略”和“心中有学生”的教育追求。对学生而言，不仅依据原有素养自主、自能和自觉地解决了实际问题，而且超越具体问题情境和阶段方法表征，通过观察对比、思维提炼和迁移运用，初步内化“从结论走向结构”的策略路径，实现了“拾级而上地学”。从发展的角度看，策略教学的起始“有模有样”，后续的策略学习必将“有形有神”。

[本文系江苏省教育科学“十三五”规划重点课题《基于问题链驱动的小学生数学化学习的研究》（课题批准文号：C-b/2020/02/26）和江苏省中小学教学研究第十三期重点课题《深度学习下小学数学游戏的开发与应用研究》（课题批准文号：2019JK13-ZB48）的阶段性成果。]

（责编 金 铃）