多空质材料机械穿透性能统计分析

胡俊宏，历 萌，宋 博，郭沛林，席春芳

(1.沈阳工业大学 机械工程学院，辽宁 沈阳 110870；2.沈阳嘉和节能保温科技有限公司，辽宁 沈阳 110100)

0 引言

装配式建筑是采用标准化构件和配件经可靠装配连接而成的建筑，相较于传统施工方式，此建筑的施工将大量现场作业内容转入工厂，是现代化生产方式的代表。2015年以来国家大力推广装配式建筑，预计2025年将达到50%以上[1]。

钢丝网架聚苯板(EPS板)是聚苯板与低碳冷拨钢丝经过焊接形成三维空间网架结构[2]的建筑构件，是装配式建筑的核心材料之一，目前广泛应用于装配式建筑复合外墙保温，具有质轻、高强、保温、隔声、抗震、施工速度快、可增加建筑使用面积等诸多优点[3]。随着国家建筑标准和建筑节能要求的不断提高，对EPS板的保温特性要求也越来越高，许多建筑中出现了150 mm以上大厚度的EPS板需求，这些需求超出了目前市场上大多数设备的加工能力。其原因在于，聚苯板微观结构的非均匀特性，使插丝穿透聚苯板过程难以预测，同时出现了聚苯板边界破损与插丝偏移现象，同时也缺少穿透力的预测公式。当前主流设备大多通过生产试验法确定插丝工艺的相关参数，这一方法在聚苯板厚度不大时具有一定的可操作性，但随着板厚的增加，穿透过程的不确定性引起的加工误差严重影响了生产效率和产品质量。同时，在要求设备具有一定加工柔性的前提下，依靠生产试验法很难确定准确的生产工艺参数。

在非均匀材料研究方面，国内外科研人员作了大量理论工作。陈星采用随机次序填充算法生成了颗粒复合材料代表性体积元特征，建立了一种基于渐进均匀化的非均质材料研究方法[4]。伍巍以二元混合颗粒体系为对象，讨论了混合体系塑性变形特征和颗粒运动的统计学特征[5]。郭进结合四叉树网格、比例边界元法提出了一种新的数值计算模型[6]。对弹黏塑性非均质材料的线性化处理中，考虑弹性与黏塑性响应的时间尺度问题，Rao W等提出了一种新的割线线性化方法，为线性化弹黏塑性本构模型提供了与弹塑性本构模型相同的数学结构[7]。张春会等考虑力学参数间的关联性，提出了基于统计学的非均质材料随机概率模型[8]。文献[9]～[11]发展了一种适合颗粒材料的高效有限元分析方法，使用Newton第二定律的显式积分算法对颗粒的运动进行了计算。张洪武[12]在周期性弹性颗粒组成的材料模型中，引入了对颗粒弹性行为和颗粒间黏着-脱离-滑动效应的考虑，建立了宏观本构模型。

本文通过搭建实验台进行了模型试验，对非均质多空质材料的穿透过程进行了统计分析，并给出了穿透力的预测公式。

1 试验设计与数据采集

EPS板结构如图1所示，多空质材料穿透过程中的穿透力按方向可分为轴向阻力和材料非均质导致的径向偏移力，前者决定了插丝电机的选取和插丝工艺参数的确定，后者产生了插丝偏移量，是影响板网成型机稳定性的主要因素。轴向阻力按来源可分解为丝-苯摩擦力和颗粒之间黏着-滑动-脱离产生的力。丝-苯摩擦力是插丝过程中插管外壁与聚苯板发泡颗粒之间相对滑动产生的滑动摩擦力；颗粒间的黏着-滑动-脱离主要表现形式为在插丝过程中压缩块的堆积与破损。

本文根据现场工况设计了模型试验，用以探索穿透过程力学模型。

1.1 模型试验设计

模拟网板成型机生产过程中多空质材料的穿透过程，按照实际工况，根据模型相似理论搭建了实验台，其机械结构见图2。实验台由驱动系统、数据采集系统、运动控制系统组成，采用57步进电机加直线运动单元模拟插丝进给运动，使用欧姆龙CP1H型PLC作为控制器，通过脉冲频率精准控制步进电机的插丝速度。采用S型荷重传感器作为力测量单元，采用数据采集卡Smacq USB-3200进行数据采集，采样频率为1 kHz。

1-上表面钢丝网;2-苯板;3-插丝;4-焊点;5-下表面钢丝网

图2 实验台机械结构

试验所选材料为密度18 kg/m3的聚苯乙烯切割板，使用304不锈钢冷拔管为穿透元件，进行单丝穿透试验，具体试验参数见表1。

表1 试验参数

1.2 数据采集结果与穿透过程分析

在进行大量试验前提下，采集的轴向穿透力部分数据如图3所示，聚苯板穿透内表面形貌和边界破损形状如图4所示。从图3轴向穿透力信号曲线可以发现，轴向穿透力信号波动较大，而从发泡材料本身特性考虑，材料中并无显著硬质点。观察图4可以发现，颗粒脱落具有显著的非均匀性，有些颗粒脱落范围远超插管直径的接触范围。因此可以得出以下结论：插管刺穿聚苯板时会破坏发泡颗粒间的黏着关系，由于插管直径与发泡颗粒直径并不存在数量级上的差异，因此，发泡颗粒会在插管前端形成不稳定的压缩块，压缩块堆积、滑移、破损使穿透力信号中出现了较强的随机波动。

图3 轴向穿透力信号

图4 聚苯板穿透内表面形貌和边界破损形状

2 试验数据的回归分析

2.1 单样本信号分析

在单次穿透试验中，得到一组轴向穿透力y(N)与插入深度x(m)的对应数据(xi，yi)(i=1,2，…，n)，其曲线如图5所示。从图5可以看出，穿透力在总体上可以分为两个阶段，初始阶段由于插管尖端形状以及压缩块堆积的影响，穿透力呈现更大的上升斜度，在深度0.025 m左右穿透过程进入较为平稳的工作状态，本文仅对平稳部分即x∈[0.025,0.2]进行分析。聚苯板的非均匀性使插管外壁与聚苯板内表面发泡颗粒间是断续接触关系，但使用pearson相关系数r对轴向穿透力与插入深度线性关系进行评估，计算得r=0.985 6，证明二者线性关联度较大，因此，可将轴向穿透力模型简化为一次函数与一个随机余项之和。

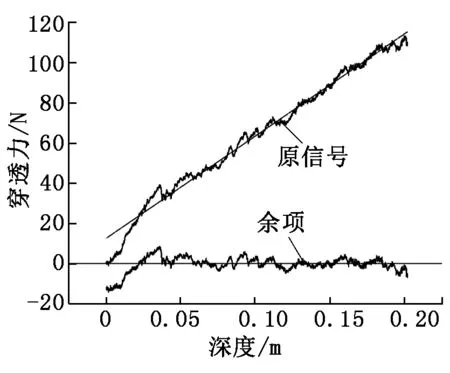
图5 单次穿透试验的轴向穿透力曲线

建立轴向穿透力的实验公式如下：

y=a+bx+Ru(x).

(1)

其中:a反映了压缩块的平均大小，其物理意义是压缩块平均所受阻力，N；b反映了摩擦项的斜率，单位为N/m；Ru(x)为随机余项。

使用最小二乘法对参数进行点估计，其计算公式如下：

(2)

(3)

将稳态部分(xi，yi)代入公式(2)，求得的各参数值见表2。使用拟合优度系数R2来度量线性回归效果是否显著，计算得R2=0.967 5，回归效果显著。

表2 拟合参数取值

图6 实验公式残差分布直方图

2.2 实验公式参数统计分析方法

由于材料非均匀性在不同单样本中累积情况不同，单样本处理得到的a和b点估计值近似正态分布。对一组样本进行2.1节处理，得到一组参数估计值，记为a1，a2，…，an及b1，b2，…，bn，其分布直方图见图7，本文通过解析法对a和b的分布母体参数进行评估。

图7 参数分布直方图

正态分布概率密度函数为：

(4)

(5)

(6)

表3 正态分布参数表

将上述值代入式(4)得参数a和b的正态概率密度函数如下：

(7)

(8)

2.2.1 可靠参数预测与评估

定义P容纳系数的参数Xp为在给定工况下容纳母体P(百分数)的参数取值，当参数分布遵循正态分布时，Xp表示为：

Xp=μ+upσ.

(9)

(10)

选取容纳系数P=95%，通过查正态分布表可知此时up=1.7，将表3数据代入式(10)可得a95=26.945，b95=643.080，因此95%容纳系数的实验预测公式为：

y95=26.945+643.080x±9.3.

(11)

选取容纳系数P=50%，得轴向穿透力中值预测模型，此时up=0，a50=17.787，b50=542.540，中值预测公式见为：

y50=17.787+542.540x±8.7.

(12)

2.2.2 模型参数正态分布的假设检验

本文中参数计算和样本容量计算都是在公式参数分布符合正态分布的前提下进行的，而实际上还应对参数正态分布进行假设检验。根据本文使用的样本容量，采用K-S检验方法进行正态分布检验，检验结果见表4。

表4 正态分布检验结果

由表3可知，pa、pb皆远大于0.05，证明在0.05显著水平下a值与b值分布显著服从于正态分布。

3 结论

本文建立了模型试验系统，对非均质多空质材料聚苯板的穿透过程进行了研究，通过大量的试验，得出结论如下：

(1) 穿透过程在插入深度0.025 m左右进入平稳阶段；

(2) 稳态阶段轴向穿透力与插入深度呈线性关系；

(3) 穿透过程中穿透力的散度较大，存在较大波动；

(4) 随机项数据近似符合正态分布规律；

(5) 本文建立了指导工业计算的穿透力预测模型，可用于指导同类材料墙板生产工艺参数的计算。