基于ANSYS的直线系统振动控制方法研究

郭沛林，胡俊宏，历 萌，宋 博，于国辉，李臣友

(1.沈阳工业大学 机械工程学院，辽宁 沈阳 110870；2.秦皇岛视听机械研究所有限公司，河北 秦皇岛 066000)

0 引言

柔性结构最早取得的成果主要是在航空航天领域[1]，与刚性结构相比，柔性结构精度更高、灵活性更好，但是在进行大范围直线运动的过程中，柔性结构在运动结束时因为自身的结构特点不可避免会产生残余振动，这将会影响系统在精密操作时的工作效率和精度。因此，有关柔性结构的振动控制一直都是相关领域的研究热点和难点[2]。

IC分拣机是用于芯片分拣的一种新型精密设备[3]，直线系统是其重要的组成部分，设备需要完成7 500次/小时的分拣动作循环，运动曲线的速度梯度变化过大将使直线系统运动平稳性降低，导致其分拣芯片动作的成功率下降，无法满足所需工作效率。因此，如何减小直线系统的柔性结构在运动结束后的残余弹性振动，对于提高直线式芯片分拣设备的工作效率有很大的研究价值。

利用轨迹规划方法抑制柔性结构运动过程中的振动属于前馈振动控制技术，它相较于反馈振动控制技术更加简单、实用[4]。近年来，丁阳等[5]基于量子行为粒子群优化算法规划出了柔性体最优运动轨迹曲线以提高定位精度；李振娜等[6]采用空间圆弧和空间直线插补设计了S型速度曲线，并将弧长增量插补方法用于轨迹规划，保证了运动曲线一阶和二阶导数的连续性。

本文首先通过试验模态分析获取柔性结构的模态参数，将其代入计算模型，同时设计4种运动轨迹，然后利用ANSYS Workbench有限元分析软件对直线系统在不同的运动曲线作用下进行仿真,求解其动态响应[7],并对振动信号进行处理分析，以验证轨迹规划方法抑振策略的可行性。

1 柔性结构模态参数试验测量与计算

为了使有限元模型的参数设置更加精确，需要对结构在装配体下进行试验模态分析，实际测量其固有频率、阻尼比和振型等模态参数[8,9]。试验采用阶跃信号响应法，与传统锤击法由力锤敲击结构提供激振力不同，本次试验采用由张拉释放的方法提供激振力，即在被测件末端用非弹性绳悬挂重物，将绳子剪断，给被测试件提供一个负阶跃响应的激励力，该方法能有效避免锤击法在试验过程中带来的双击影响。试验所用仪器为ECON亿恒测试系统，加速度传感器的型号为东华1A102E，测试现场如图1所示。

图1 测试现场

通过在工作位置点上安装的加速度传感器拾取加速度信号，并传输至测试分析软件平台，经过多次测量，试验结果取平均值，加速度时域信号通过FFT(快速傅里叶变化)得到工作位置点的幅频特性响应曲线，并将高频噪声过滤。得到的幅频特性响应曲线如图2所示。

图2 幅频特性响应曲线

通过观察幅频特性响应曲线的峰值点，可以得到柔性结构前6阶的模态参数，如表1所示。

柔性结构的刚度阻尼计算公式为：

(1)

其中：βn为结构的n阶的刚度阻尼；ξn为结构的n阶阻尼比；ωn为结构的n阶固有频率。

将1阶阻尼比和1阶模态频率代入式(1)得到β1=1.41×10-4。

从表1数据可以看出，直线系统前6阶固有频率主要集中在113 Hz～903 Hz。设备的工作频率为3.3 Hz左右，所以直线系统的往复运动工作频率不会激起结构的共振。

表1 柔性结构前6阶模态参数

2 运动曲线规划

一般轨迹规划的运动曲线都采用直线、圆弧、多项式曲线等插补方式进行设计。根据不同曲线的形状与实际工作需求，设计了4种运动轨迹的速度曲线，如图3所示。实际工作行程为400 mm，将起点和终点的速度为0作为边界条件，运行时间为0.3 s。

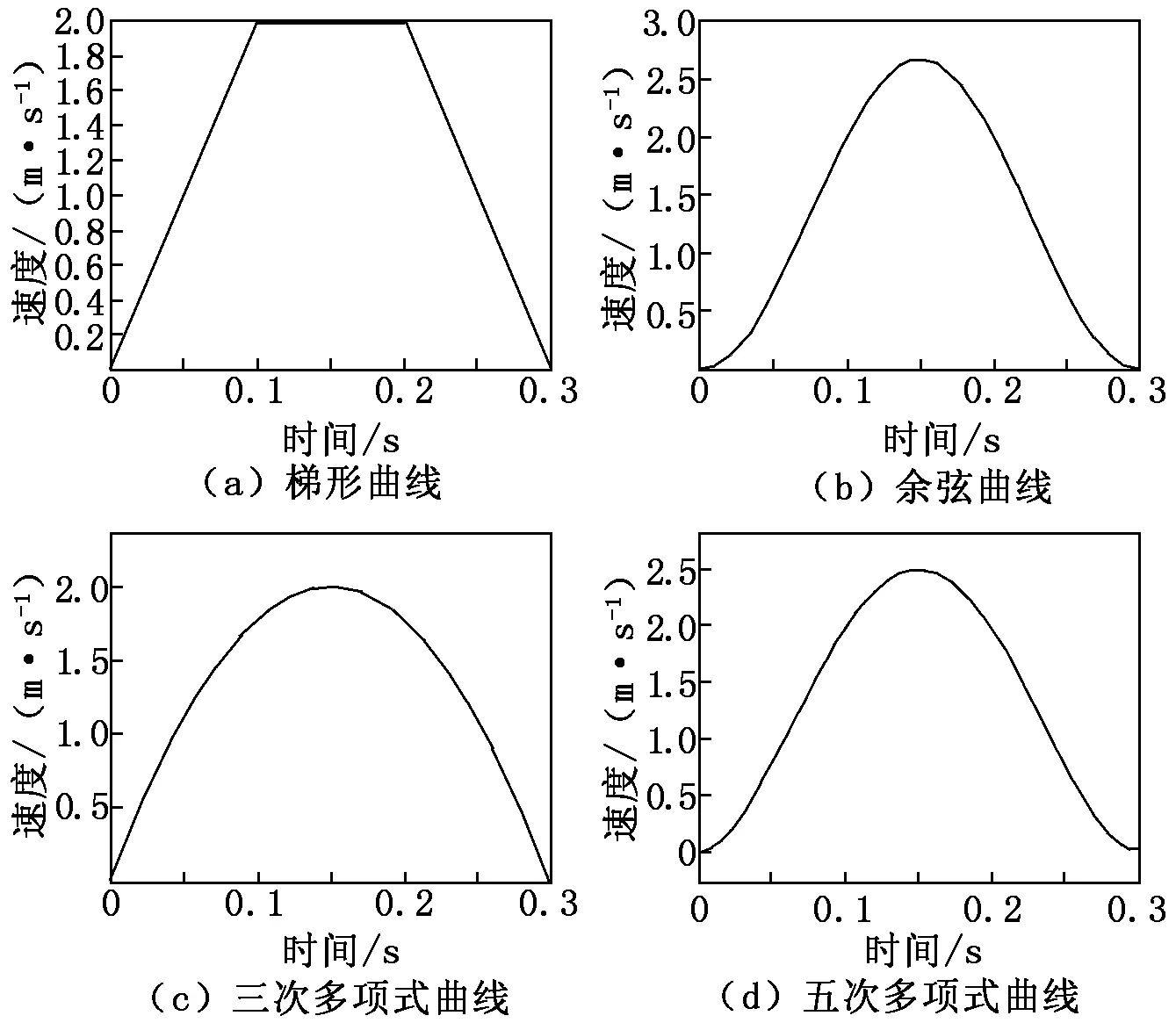
图3 4种运动轨迹的速度曲线

4种运动曲线的表达式如下：

(1) 梯形曲线：

(2)

(2) 余弦曲线：

v2(t)=-1 333.3cos(6.67πt)+1 333.3
0≤t≤0.3.

(3)

(3) 三次多项式曲线：

v3(t)=2 666.67t-8 888.89t20≤t≤0.3.

(4)

(4) 五次多项式曲线：

.

(5)

其中：t为系统运行时间；v为系统运行速度。

4种运动曲线的加速度梯度变化不同，且起点和终点位置处的加速度不同，能够更好地探究运动曲线性能参数对直线系统残余振动的影响。

3 有限元模型的建立

直线系统由直线电机牵引器和吸嘴结构组成。针对IC芯片分拣机的实际工作需求，直线系统沿横向移动距离最远为400 mm。在建立有限元模型时，为了方便吸取芯片，选取L型短梁结构作为吸嘴结构，材质选用质量轻、强度高的7075铝合金；直线电机简化为质量块，对模型进行适当的简化，以减少仿真分析所需时间。表2为L型短梁的具体参数。

表2 L型短梁基本参数

在刚柔耦合动力学分析中，刚体结构牢固，能够承受较大的冲击而不会产生变形；而柔性结构在载荷作用下产生小位移和小应变。本文将直线电机设置为刚体结构，L型短梁设置为柔性体结构，总体网格尺寸采用3 mm，端部为工作点位置，进行网格加密处理，控制尺寸为2 mm。本次仿真计算中采用了四面体单元，网格总数目为18 825 ，节点总数目为9 441，整体网格精度较好，可以进行精密计算。直线系统整体网格划分如图4所示。

图4 直线系统整体网格划分

4 瞬态动力学仿真

4.1 载荷及约束设置

为了保证仿真结果与实际工况的一致性，需要对直线系统施加载荷和约束。首先，将中心刚体与柔性结构之间的接触关系设置为绑定，使其不产生相对滑动。同时，与地面沿X轴方向创建一个移动副，使得直线系统只存在沿着X轴方向的自由度，并对机构添加了沿Y方向的重力加速度，如图5所示。

图5 直线系统的载荷及约束

利用ANSYS Workbench瞬态动力学仿真的目的是为了得到系统运动停止后的定位精度，瞬态动力学综合考虑了惯性及阻尼的影响，适用于分析结构的应力及位移等在已知动态载荷下的变化。综合考虑计算时间与精度，设置计算时间总长为0.35 s，前0.3 s为系统运动400 mm所需时间，之后的0.05 s为系统运动结束后工作位置点残余振动时间；由于本文主要研究系统的残余振动，所以将系统的前0.3 s划分为1 000个子步，运动结束后的0.05 s划分为5 000个子步，能够有效地减少计算时间。

在ANSYS中计算求解主要应用New mark时间积分法，在计算过程中若不设定阻尼，在对高频结构计算时会产生数值躁动，严重影响仿真结果，所以需要将上节计算得到的刚度阻尼代入到计算模型。

4.2 仿真结果分析

将瞬态动力学仿真数据导入MATLAB进行数据处理，柔性结构工作位置点在4种运动曲线下0.3 s～0.35 s的位移时程曲线如图6所示。

图6 4种运动曲线的工作位置点位移时程曲线

以梯形运动曲线残余振动位移曲线为基准，其振幅衰减97%时，视为振动停止。工作位置点位移时程曲线对时间的积分为残余振动耗散的能量。时域分析结果如表3所示。表3中，“—”代表曲线不可导。

表3 工作位置点在不同运动曲线下的时域分析结果

由于系统的传递函数能够描述线性结构特性，取决于系统自身的结构特性，与外部输入无关[10]，因此，将仿真得到的系统响应数据通过参数辨识算法可以得到输入为激励力信号、输出为柔性结构末端振动位移的传递函数H(s)：

(6)

其中：Y(s)为拉氏变换后的位移响应信号；F(s)为拉氏变换后的激励力。

将传递函数转换到频域上进行分析，即对时域函数H(s)进行傅里叶变换得到位移频率响应函数H(ω)：

(7)

其中：Y(ω)为傅里叶变换后的系统输出信号；H(ω)为傅里叶变换后的输入信号；ω0为系统的固有频率；ξ为系统的衰减系数；K为系统的静态灵敏度。

从图6可以观测到，柔性结构在运动停止后有明显的残余振动，随后，在阻尼的作用下，各曲线逐渐平缓。根据表3数据可知，在三次多项式运动曲线和梯形运动曲线下直线系统弹性振动消除的时间约为五次多项式运动曲线和余弦多项式运动曲线3倍，这是由于三次多项式运动曲线和梯形运动曲线的起始和终点位置处一阶和二阶导数不连续导致的，加速度曲线梯度变化过大将导致柔性结构受到的激励力增加，结构运动停止时的残余振动幅值变大。

通过对4组仿真数据进行对比可知：保证运动曲线的一阶和二阶导数梯度变化的连续性将明显减小残余振动的振幅，证明了合理规划S型运动曲线抑振方法的可行性，为提高直线系统的精密操作稳定性和工作效率提供了理论基础。

5 结论

(1) 本文针对直线系统，在装配体状态下通过试验模态分析实测其模态参数，并代入有限元计算模型，保证了有限元模型参数的真实性。

(2) 对系统在4种运动曲线下的运动过程进行了动力学仿真分析，仿真结果表明系统在五次多项式运动曲线下振动停止时间最快，在余弦多项式运动曲线下的振动幅值最小。

(3) 验证了轨迹规划抑振策略的有效性，通过控制运动曲线速度梯度变化的连续性，柔性结构运动结束时的残余振动幅值将被有效抑制，且稳定所需时间减少，极大地提高了直线系统运动的平稳性，保证了直线系统分拣芯片动作的成功率与工作精度。

本文研究成果将有助于设计IC芯片分拣机的直线系统，同时也为线性系统的振动控制技术提供了新的思路与尝试。